船用LNG储罐纵荡过程瞬时液体冲击分析

陈雷，张克正，封星

(1.烟台职业学院 汽车与船舶工程系，山东 烟台 264670；2.鲁东大学 交通学院，山东 烟台 264025； 3.大连海事大学 轮机工程学院，辽宁 大连 116026)

0 引言

液化天然气(liquefied natural gas,LNG)动力船舶营运时，非满载燃料储罐内部自由液面会受到船舶营运状态及外界作用力的影响而呈现非线性和不规则的复杂运动形态[1]，对储罐壁面产生巨大的液体冲击力。液体冲击可能造成罐体破裂、液体泄漏等事故，对船员与船舶的营运安全带来严重危害[2-5]。目前，国内外对燃料储罐内部冲击的研究多集中于比对数值模拟与试验工况下的液面振型，以此来证实数值模拟的正确性与适用性[6-9]，或者是观察液体冲击时，黏度、密度、加速度等参数变化对罐体内部液体的动压力和自由液面波动情况的影响，但很少分析充注率与容积变化对罐内冲击力的影响，或直观揭示液体最大冲击力与各影响因素之间的具体关系[10-15]。

本文以30 m3卧式筒形LNG燃料储罐为研究对象，模拟罐内液体纵荡时充注率和容积对罐内最大冲击力的影响，并将其与惯性力进行比对，分析最大冲击力与惯性力之比随参数变化的规律，进而得到最大液体冲击力与影响因素的关系。

1 建模

图1 储罐模型

液体纵荡冲击的根本原因是储罐内部自由液面导致的晃动。晃动与储罐内部液体的充注率、容积以及液体的黏度、密度、加速度等参数存在很大关系。研究对象为容积为30 m3的C型LNG储罐，长8270 mm，内径DN=2200 mm，筒体长(不包含封头直边)7090 mm，采用标准椭圆封头。设定坐标原点于罐左侧(后端)封头顶点位置，x轴正方向为船舶艏部方向，y轴负方向为重力方向，z轴方向为船舶左右舷方向，如图1所示。假定罐体是刚体，壁面无滑移，不考虑气-液分界面的表面张力。

在Fluent求解器中采用瞬态模型，湍流模型采用标准k-ε模型，多相流模型采用流体体积函数，即目标流体的体积与网格体积的比值(volume of fluid，VOF)模式，采用速度与压力耦合PISO算法[16]；对流项离散格式采用一阶迎风，压力的空间离散采用体积力加权(Body-Force-Weighted)方式，采用UDF程序加载定义动量源项，对流体施以加速度。

根据求解器设置与流体动力学要求，得到罐内液体纵荡应遵循的基本方程[17]。

1)连续性方程

式中：ρ为流体密度，t为流动时间，u、v、w为速度矢量在x、y、z方向上的分量。

2)动量平衡方程

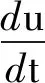
式中：t为时间，s；ρf为单位体积力作用于流体质量上的非接触力；p为流体流场的压力；τ为黏性应力分量，σ为应力张量，可以表达为：

3)湍流动能方程k与扩散方程ε表达式分别为：

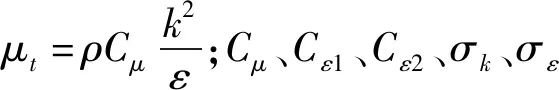
2 模型验证

2.1 流体网格验证

图2 储罐初始内部静压强分布

高质量的网格是Fluent计算湍流运动的必要条件[18]。流体空间采用六面体网格形式，共60 988个，为验证划分网格的精确度，暂不对流体施加速度边界条件。介质的类型、黏度对介质晃动的影响极小，在研究液体晃动时，国内外学者多采用理想无黏性介质。因此，储罐内部以水和空气为流体介质，替代LNG，定义水和空气的体积比为1：1，初始化后观察储罐内部静压强的分布(如图2所示，浅灰色为液相，深灰色为气相，图中单位为kPa)，并与计算理论值进行比对[19]。

由图2可见：罐内压强分布层次清晰，自罐顶到罐底呈线性分布，罐底静压强最大，为10.4 kPa。

最大理论静压强

Pmax=ρgh，

式中：ρ为液体密度,g为重力加速度,h为液体深度。

根据储罐尺寸与充装率可计算储罐内部Pmax=10.8 kPa。

计算静压强与理论静压强非常相近，故流体网格符合要求。

2.2 参数设置验证

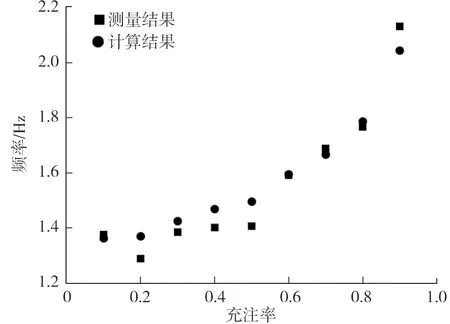
图3 纵向晃动频率的计算结果与测量结果对比

为验证模型参数设置的正确性，参照文献[6]中的参数建立罐体模型，计算不同充注率下内部介质的纵向晃动频率，并与测量结果进行对比，如图3所示。

由图3可知:在充注率为0.1～0.9时，内部介质纵向晃动频率的计算结果与试验测量结果较为吻合。只在充注率为0.2时两者偏差最大，偏差为4.91%。因此，计算结果具有较高的可信度，参数设置可行。

2.3 案例计算

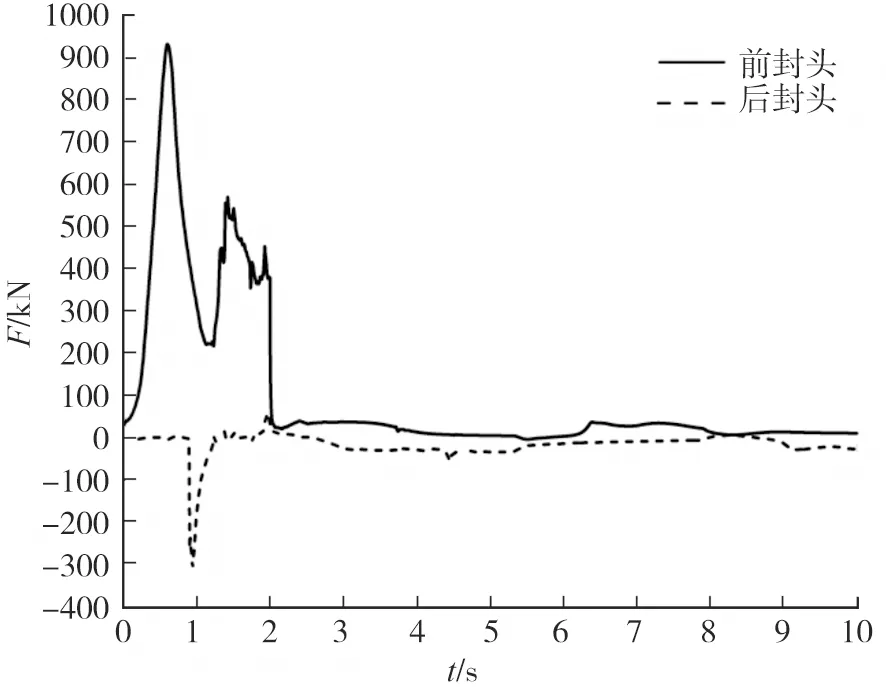
图4 储罐前后封头纵向液体冲击力时域响应

文献[10]证明以水作为液体介质进行研究有一定的通用性。现以水与空气作为介质，模拟LNG动力船舶在制动过程中燃料储罐内部液体纵向晃动过程，观察储罐内部液体冲击力的变化。文献[20]规定，沿船舶运动方向向前和向后碰撞的最大设计加速度为2g。假设在时间t=0时，对充注率为0.50的罐内流体沿运动方向施以2g的加速度，使内部液体与储罐产生相对速度，内部产生晃动；在t=2 s时将加速度减为0，观察0～10 s内罐中液体与空气的晃动情况，监视整个晃动过程中前后封头所受液体冲击力F随时间的变化规律，结果如图4所示。

图5 t=0.60 s时储罐内部气-液两相体积分布

由图4可以看出：当船舶采取紧急制动或碰撞后，储罐内部液体向前移动冲击前侧封头，在t=0.60 s时，前封头液体冲击力出现峰值，Fmax=932.179 kN，此刻气-液两相分布如图5所示(图中为气体体积分数，浅灰色为液相，深灰色为气相)。在t=0.945 s时，后封头液体冲击力达到最大值，Fmax=307.446 kN，仅为前侧封头受力的1/3。在t=2 s，即加速度减为0的瞬间，前后封头受力突然降低，罐内介质进入自由晃动阶段，冲击力维持在较小范围内变化，并逐渐趋向于0。这与船舶制动时罐内介质的运动状态相符，因此，模型是可信的。

3 液体冲击影响因素分析

本文主要研究液体冲击力对储罐及船舶营运安全的影响，故只监测前后封头最大液体冲击力Fmax，并将其与介质惯性力F0进行比较，找出液体冲击力的变化规律。定义介质惯性力

F0=ma=ρVa，

(1)

式中：a为加速度，m为液体惯性质量，V为液体体积。

定义放大系数

(2)

定义绝对偏差率

(3)

此前，学者们针对密度、黏度、加速度等参数与储罐内部液体冲击力的关系进行了大量试验与研究，结果表明：在其他参数保持不变的情况下，最大液体冲击力与黏度无关，与密度及加速度呈线性正比关系，液体冲击放大系数不随密度、黏度、加速度的变化而变化。本文主要分析储罐容积与充注率对罐内液体冲击的影响，探讨放大系数的变化规律。

3.1 储罐容积

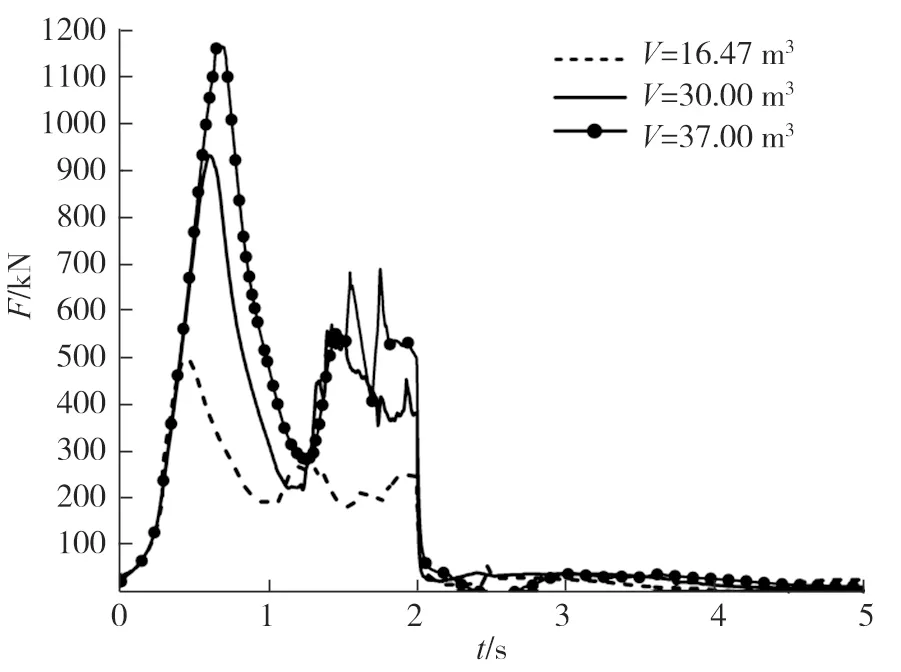
图6 不同储罐容积纵向冲击力的时域响应

不同型式燃料储罐的区别主要是罐体长度，而储罐直径相差不大。保持其他参数不变，计算不同储罐容积对纵荡过程的液体冲击力。针对内径DN=2200 mm的标准椭圆封头储罐，选取长度L分别为4700、8270、10 100 mm的储罐作为研究对象，对其晃荡过程进行数值模拟，观察不同容积储罐内部瞬时液体冲击力的时域响应，如图6所示。

由图6可以看出：储罐容积不同时，瞬时最大液体冲击力的出现时刻随储罐容积的增大而滞后；当储罐容积增大时，储罐内部瞬时最大液体冲击力随之增大。

不同工况下瞬时Fmax出现时间、F0及K等数据如表1所示。

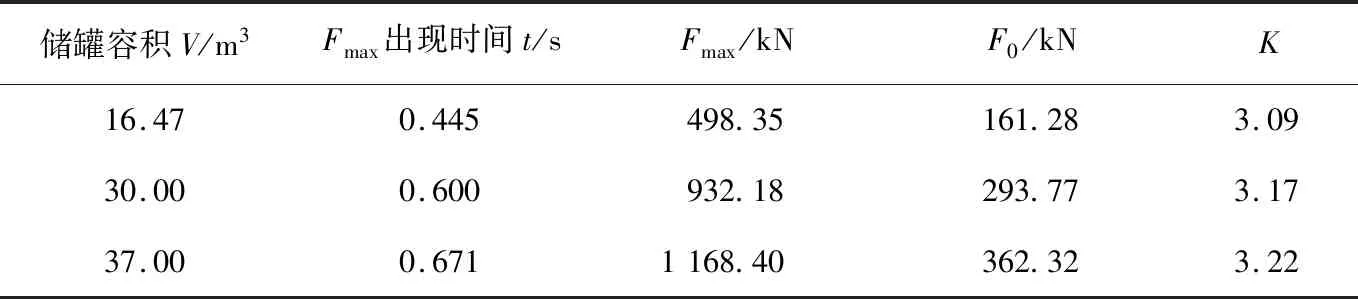
表1 不同储罐容积的液体冲击参数

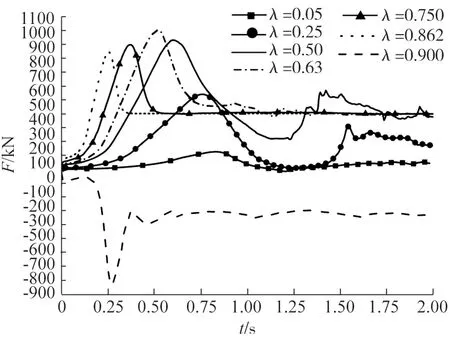
图7 不同充注率下纵向冲击力的时域响应

从表1可以看出：若液体密度、黏度、加速度等参数保持不变，最大液体冲击力与容积成线性正比关系。在容积发生变化时，K平均为3.16，最大偏差为2.3%，随容积变化不大。

3.2 充注率

文献[21]规定，C型LNG燃料储罐的充装极限不大于90%，因此，充注率λ≤0.90。现分别模拟充注率λ为0.05、0.25、0.50、0.63、0.75、0.862、0.90等7种工况下的内部介质晃动情况，观察不同充注率下冲击力的时域响应，如图7所示。

从图7可以看出，随着充注率的增大，最大液体冲击力出现的时刻不断提前，这是因为充注率增大后，液体与前封头的接触面积增大，向其运动进行冲击所需时间减少。λ接近极限充注率0.90时，最大冲击力没有出现在前封头位置，而是出现在后封头位置，相应时间也有所延迟。不同充注率下液体Fmax出现时间与k等参数数据，如表2所示。

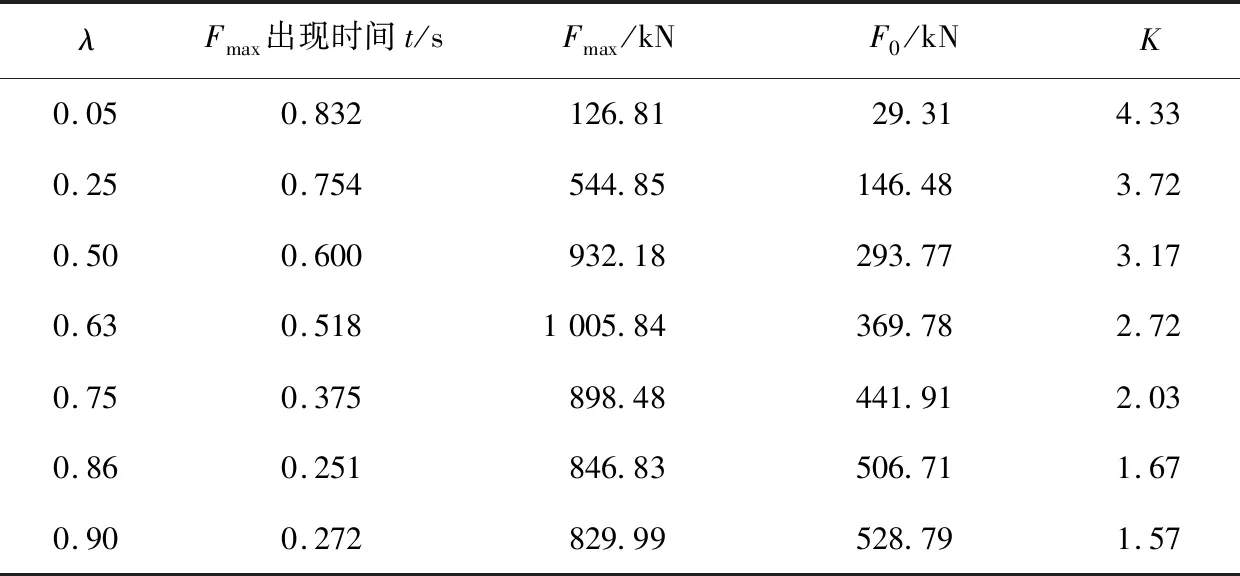
表2 不同充注率时液体的冲击参数

图8 Fmax、K随λ的变化曲线

Fmax、K随λ的变化曲线如图8所示。

由图8可知，K与λ呈多项式函数关系，随λ的增大而减小。储罐受到的Fmax呈现先增大后减小的趋势：在λ较小时，液体冲击力随λ的增大而增大，这主要是受到液体惯性力增加的影响；在λ达到0.63左右时，Fmax达到极值后呈下降趋势，这是因为λ较大时，罐内液体不像低充装率时在罐内翻腾晃动，此时，介质涌向前封头的时间明显缩短，液体全部涌向前封头，气体被挤压至后封头位置，储罐内部的液体冲击力很快达到稳定值。

4 结果分析

4.1 拟合关系式

通过液体冲击影响因素分析可以看出，液体冲击放大系数与容积、黏度、密度和加速度无关，与充注率呈一定函数关系。根据放大系数随充注率变化曲线的特点，拟合充注率不同时放大系数的变化曲线，采用多项式表示K-λ曲线为：

K=f(λ)=a1λn+a2λn-1+…+anλ+an+1，

(4)

式中：n为多项式的最高次幂；ai为幂次降序的多项式系数，i=1，2，…，n，n+1。

定义a=(a1a2…anan+1)为多项式系数，λ=(λn,λn-1,…λ,1)T为高度幂矢量，则可用矩阵表达为：

K=aλ。

采用Matlab软件的指令格式f(λ)=polyfit(λ,N,n)，对已知的λ和K的离散数据及最高幂次n(n取2～5)进行最小二乘多项式曲线拟合，得到系数a，得出2～5次多项式的拟合曲线特性方程[22-23]。表3中列出了不同最高次幂的最大偏差，从最大偏差可以看到：4次多项式的拟合偏差为2.74%，更高幂次的

表3 不同幂次拟合曲线偏差

拟合精度也没有得到显著提高，而且会使拟合曲线的光滑性变差，多项式出现摆振特性，反映更多的数据量化误差[24-25]。

由此确定：

K=23.714 4λ4-46.584 9λ3+28.133λ2-
8.365 2λ+4.684 3。

(5)

结合式(1)～(5)，可得Fmax与F0的关系式为：

Fmax=(23.714 4λ4-46.584 9λ3+28.133λ2-8.365 2λ+4.684 3)F0。

(6)

4.2 结果验证

现数值模拟5种不同介质在容积、加速度、充注率等不同工况下的结果，验证式(6)的正确性与适用范围，对比结果如表4所示。

表4 Fmax-F0关系式验证比对

图9 不同形状燃料储罐纵向冲击力时域响应

由表4可以得到：定容积燃料储罐沿运动方向制动时，内部介质最大冲击力的计算公式数值模拟的计算误差均在2%以内，符合工程精度要求；关系式(6)在不同容积、不同介质、不同加速度、不同充装率等条件下都是有效的。为了验证式(6)的适用性，针对不同形状的燃料储罐进行数值模拟，选择30 m3方形储罐与平封头储罐进行验证，给定液体的充注率λ=0.50，加速度为2g，模拟计算结果如图9所示。

从图9中可以看出，储罐的形状对储罐内部最大液体冲击力影响较大，不同形状的储罐最大冲击力不同，与公式计算结果Fmax=938.30 kN偏差较大，故上述冲击力计算公式并不适用于不同形状的燃料储罐。

5 结论

1)针对标准椭圆头筒型储罐的内部液体冲击，采用单一变量法，分析容积、充注率对最大瞬时液体冲击力的影响。结果表明：最大瞬时液体冲击力的出现时刻随储罐容积的增大而滞后，随充注率的增大而提前；最大瞬时液体冲击力随容积的增大而增大，随充注率的增大呈现先增大后减小的趋势。

2)通过分析仿真结果得出最大冲击力与介质惯性力的关系式，表明：放大系数与充注率呈4次多项式关系，与容积、黏度、密度和加速度等参数无关。

3)分析拟合的Fmax-F0关系式的适用性。结果表明：针对标准椭圆头筒型储罐，关系式在不同容积、黏度、密度和加速度下都是有效的，计算误差在2%以内，符合工程精度要求，但不适用于其它形状的储罐。