双导体球在匀强外电场中的空间电场分布

董延更 赵佳羿 王 飞

(郑州大学物理工程学院，河南 郑州 450001)

导体球或球壳在匀强外电场中的场强分布是电动力学中的经典题目，也是大家所熟悉的题目，但均匀电场中出现两个导体球或球壳(二聚体)时的场强却少有讨论。两导体球电极化所引起的导体球间电磁场的局域增强是表面等离激元增强和针尖等离激元增强最基本的特性之一，也是表面增强光谱的最主要原因。本文通过对单个导体球在均匀外电场中的场强分布和性质的求解分析，考虑在均匀外电场中沿电场线方向引入两个导体球，并对其电势场强进行计算分析，再用Matlab软件画出直观的电势场强图像，进一步讨论了在匀强电场中两导体球之间间距和电场局域增强的关系。通过对这一电动力学经典习题的分析和扩展，增进对表面增强光谱的初步认识和了解，同时锻炼对计算物理和Matlab计算软件的运用能力。

1 问题引出

首先，简要讨论均匀电场中导体球的外电场分布。

设有一半径为R0的接地导体球置于均匀外电场E0中。导体球使空间分为两均匀区域——球外区域和球内区域。球外区域没有自由电荷，因此电势φ满足拉普拉斯方程。由球坐标系中拉普拉斯方程的通解，代入后可得球外电势为

(1)

其中an,bn为待定常数，由边界条件确定。最后可得到球外电势为

(2)

再对电势求负梯度，得到球外的电场强度为

(3)

这是电动力学教材中的典型例题[1]。由式(3)可以看出，导体球外靠近导体球表面的电场由于导体球在外电场的作用而重新分布。球外电场线在球表面处比原有均匀场密集，即电场线向导体端面会聚。分析发现沿外场方向的导体球端点处的电场强度是均匀电场强度的3倍，而垂直外场方向的导体球端点处的电场强度接近零。

考虑到导体球端点处的电场强度是外加均匀电场强度的3倍，电场强度极大地增强了。可以引入一个有趣的问题：如果在均匀外电场中，沿电场线方向放置两个相近的导体球，那么球外电势和电场强度的分布会如何，电场强度能增大到多少倍？这一问题可以看作表面等离激元增强和针尖等离激元增强等科研前沿的简化模型，即电子显微镜针尖和纳米颗粒之间的相互作用。课堂上通过从科研前沿和实验技术引入这一问题，可以增加学生学习电动力学的兴趣和锻炼学生对计算物理和Matlab计算软件的运用能力[2]。

2 问题求解

如果采用求解拉普拉斯方程的办法求解双球问题，无论在双球坐标系还是切球坐标系中进行，通常会因繁琐的分离变量过程而束手无策。而镜像法是电动力学中一种常用的数学方法，可以避免对拉普拉斯方程复杂繁琐的求解。下面使用镜像法来求解均匀电场中双导体球的空间电势。

图1 (a) 导体球和一个点电荷的镜像法示意图；(b) 匀强电场中单个导体球的镜像法示意图

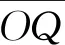
(4)

由几何关系可以得到，只要选取Q1的位置使△OQ1P∽△OPQ，那么满足

(5)

由三角形相似关系式(4)和式(5)可以得出，

式(6)、式(7)分别确定了由Q1像电荷在导体球内部的位置和电荷大小。如果导体球不接地，要同时满足上述边界条件和导体球总电荷为零条件，那么在球心O添加一电荷量为-Q1的点电荷即可。

外加匀强电场可以看成是两个相距无限远的等量异号点电荷在其连线中点处产生的电场[3]，单个导体球的静电感应现象，如图1(b)所示，由对称性条件与式(6)和式(7)可以得出，由±Q产生的两组像电荷在球心处的叠加为零，球内像电荷大小和距球心距离为

(8)

a趋向于无限大，则b趋向于零，因此在匀强电场中的像电荷可以看作一对电偶极子，其偶极矩p的大小为

(9)

由±Q在导体球表面产生的电场大小为

(10)

式(10)和式(9)联立消去Q/a2得，

(11)

其中p的方向和E0方向相同。这与教材和其他文献中单介质球的结果一致，其中的导体球可以看作介电常数为无限大的介质球[1-4]。

下面看电偶极子在导体球中产生的像电荷，其模型如图2所示。

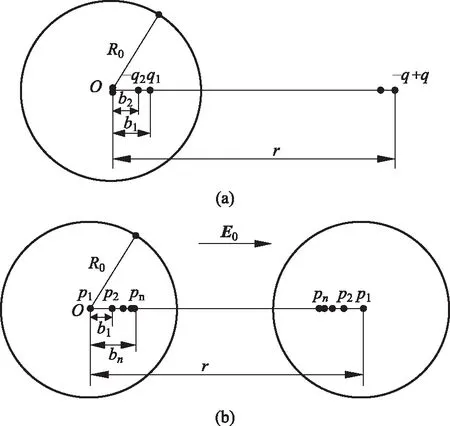
图2 (a) 电偶极子在空间一个导体球时产生的像电荷；(b) 两个相同导体球时产生的像电荷

取+q和-q的间距为Δl，由式(3)、式 (4)可以得出电荷-q的像电荷q1和-q1，电荷+q的像电荷q2和-q2的大小和位置(其中-q1和q2在球心处):

(12)

对于电偶极子p0，Δl应为一无穷小量，满足：

因此电偶极子在球心处的像电荷为零，另外两个像电荷组成一对电偶极子，其偶极矩为

(15)

如图2所示，当空间电场方向有两个相同导体球时，由于空间中电场作用，会在两球心位置各产生一对像电偶极子p1，其偶极矩大小可由式(11)给出。像电偶极子p1会分别在另一个导体球中产生次级的电偶极子p2，接着产生p3…pn就像两面镜子一样无穷反射下去[5]。

由式(11)、式(14)、式(15)得出下表：

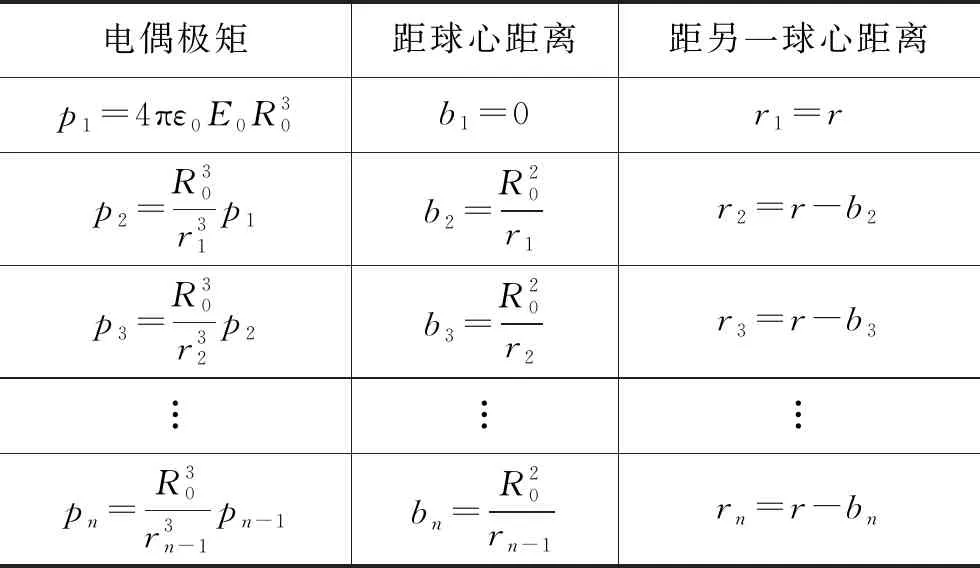
电偶极矩距球心距离距另一球心距离p1=4πε0E0R30b1=0r1=rp2=R30r31p1b2=R20r1r2=r-b2p3=R30r32p2b3=R20r2r3=r-b3︙︙︙pn=R30r3n-1pn-1bn=R20rn-1rn=r-bn

由上可以得到两相同导体球在均匀电场中的镜像电荷分布情况，空间电势情况只需要将所有像偶极子的电势和匀强电场的电势叠加即可。

(16)

导体球表面上电势处处相等，其电势可由边界电势得出。由静电场唯一性定理及此处级数表达式可得出此电势是收敛的。

当y=0时，得到x轴上的电势分布为

(17)

对电势求负梯度，便得到x轴上的场强分布：

(18)

3 结果讨论

3.1 空间中电势和电场强度分布

上面通过计算得到了均匀电场中沿电场线两导体球外的电势和电场强度的分布。下面通过Matlab作图来直观地分析空间中球外的电势和电场。

令两球心距离r=10m,E0=5N/C,金属球半径R0=2.5m，并取多项式(16)的前100项作空间电势方程的近似解。得到xOy平面空间等势线图像，如图3所示。图中A点、B点为两金属球沿x轴线方向在表面上的点，C点为沿x轴线两球心的中点。

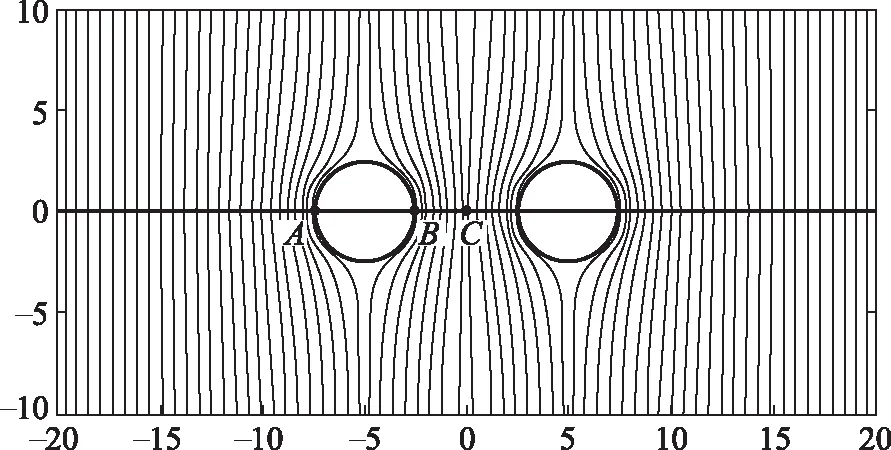
图3 均匀外电场中两导体球球外空间的电势示意图

图3中两个圆为金属球边界，可以看出边界处于一条等势线上，因此满足上述边界条件。由静电场的唯一性定理可知，上述函数φx,y满足金属外部空间电势分布，是正确的解。

使用Matlab对函数φx,y进行梯度运算，可以得到电场的分布及其大小。将球内电场强度置零，可以得到空间中各位置电场强度的大小，如图4所示。图4中可以看出，在无穷远处电场强度恒定为E0，在沿电场线方向的金属球边缘处的电场强度会明显增大。这正是由于空间电场的电极化作用和两球之间的库仑力相互作用使球体产生感应电荷，其作用可用无限对电偶极子代替。

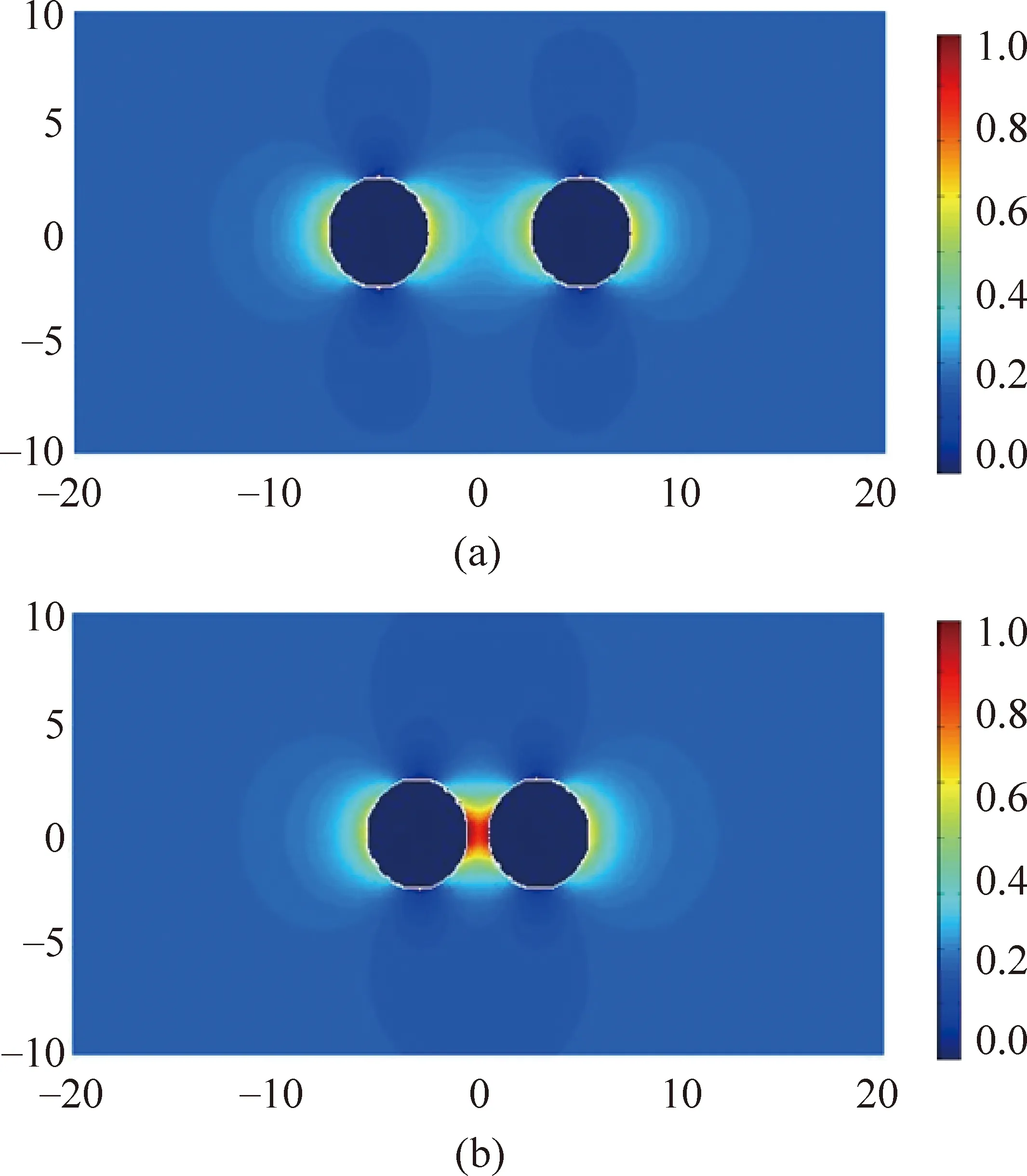
图4 均匀外电场中不同距离两导体球外的电场强度大小分布(图4(a)球心距离为10m；图4(b)球心距离为6m)。色带从0.0到1.0表示强度从零到最大

在图4中，两球心连线上电场强度的分布关于中心点C对称(其中A、B、C点位置同图3)。在图4(a)中，趋于两导体球外端表面A点处的电场强度明显增强。靠近导体球表面的B点处的电场强度强同样明显增强，而在两导体球中心处C点的电场强度稍弱。电场在导体球靠近中心处B点的场强稍稍大于该导体球另一端的A点处的场强(如图5)。这说明在均匀电场中导体球的旁边再放一个导体球时，会使原来那个导体球端点处的电场强度进一步增强。并且随着两球心距离的缩小，B点和C点的电场强度将会进一步增强。

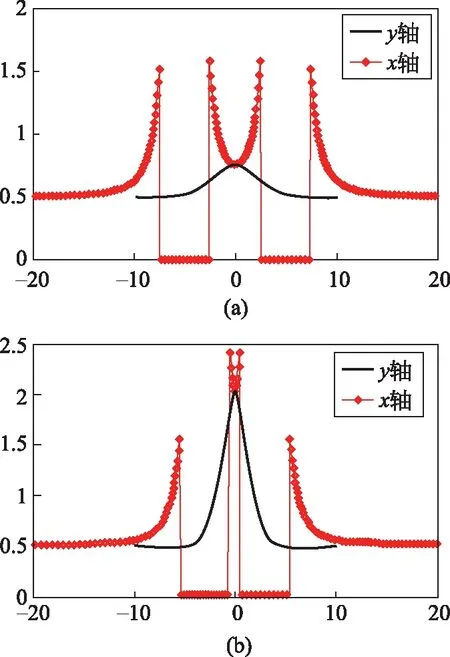
图5 均匀电场中不同距离两导体球x轴上的场强分布(图5(a)球心距离为10m；图5(b)球心距离为6m)

3.2 x轴上A、B和C点处电场强度

当移动两个导体球，改变两导体球的相对位置时，会发现x轴上导体球附近的场强发生明显变化(如图4，图5)。固定A、B和C3点为球心连线上金属球表面上两点和球心连线中点，分别求出这3个点的电场强度随两导体球的相对位置R0/r的值，如图6，得到如下结果：

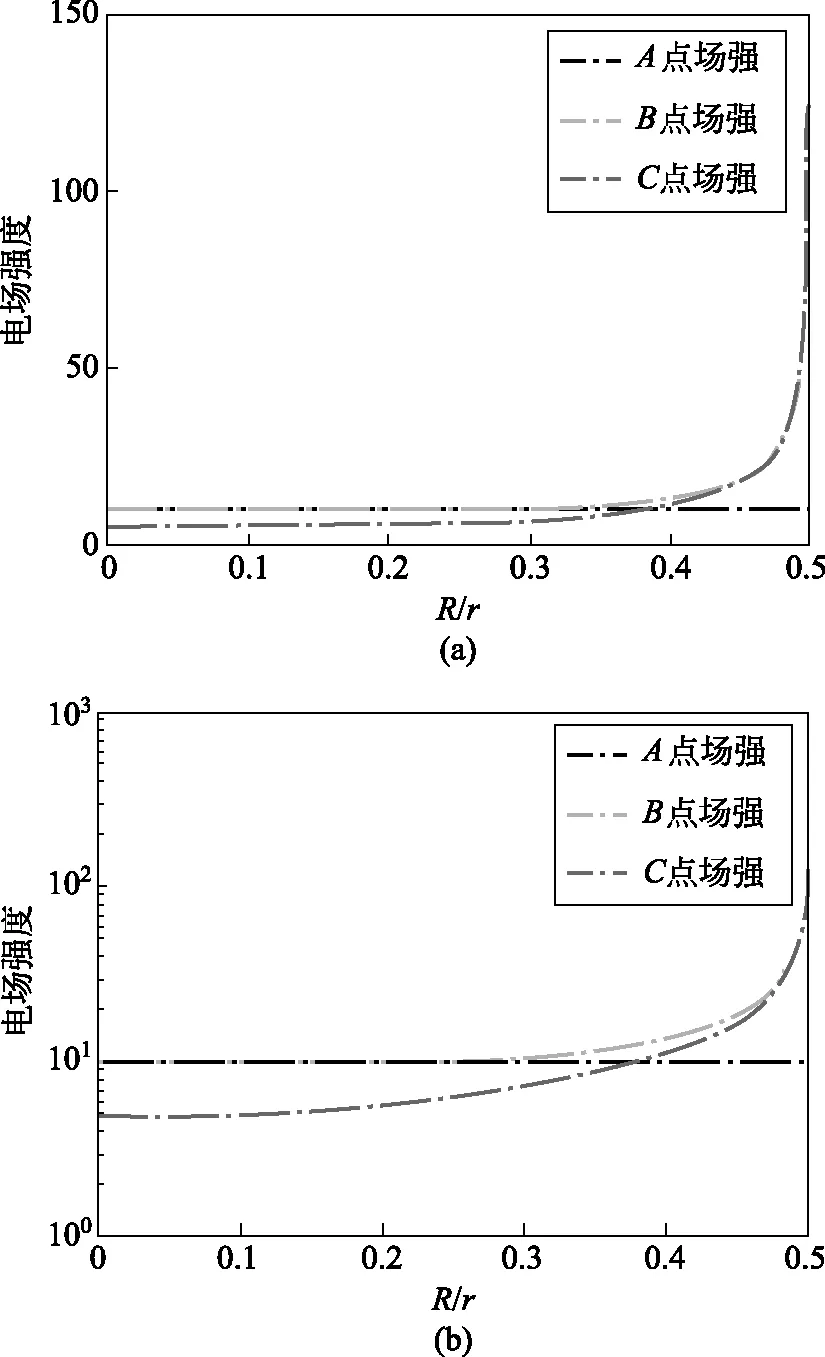
图6 (a) x轴上A、B和C 3点处电场强度随R/r的变化；(b) 电场强度以10为底的对数

(1)x轴上第一个导体球的左端A点处的电场强度：当两导体球相距无穷远时，A处的电场强度为均匀场强的3倍，这与单个导体球在均匀电场处的情形相同；而当两个导体球相互靠近时，A点处的电场强度有所增加，但变化不明显。

(2)x轴上第一个导体球的右端B点处的电场强度：当两导体球相距无穷远时，B处的电场强度为均匀场强的3倍，这与单个导体球在均匀电场处的情形相同；当两个导体球相互接近时，一开始B点处场强的增强不明显(如图4(a))；但当两导体球心间距离小于2.22倍球半径后，B点处的电场强度随相对位置R0/r的增加发生指数形式的增长。特别是当两导体球无限接近时，B点处的电场强度达到极值。其中，当两导体球球心间距离为2.0002倍导体球半径时，B点处的电场强度为均匀电场强度的100倍。

(3)x轴上两导体球中心C点处的电场强度：当两导体球相距无穷远时，C点处的电场强度为均匀场强，这说明此时该点处的电场强度基本不受两个导体球的影响。当两个导体球相互接近时，一开始C点处场强的增强不明显,但当两导体球心间距离约为2.6倍导体球球半径时，中心C点处的电场强度开始大于x轴上第一个导体球的左端A点处的电场强度。在这以后，C点处的电场强度增加越来越快，最后也呈现指数增长。

(4) 用Matlab作出x轴上A、B和C3点处电场强度以10为底随R0/r的指数变化(如图6(b)所示)。可以看出：A点处的场强变化不大，B点场强在当两导体球心间距离小于2.22个球半径后的增长速率大于指数增长，C点一开始增长速率与指数增长相似但后来的增长速率也超过指数增长。

4 结论

本文从电动力学的经典题目——均匀电场中一个导体球在端点处的电场强度是外加均匀电场强度的3倍出发，提出均匀电场中存在两个导体球时的问题，通过模型求解和数值计算对问题进行详细的分析讨论。发现当两导体球球心间距离为2.0002倍导体球半径时，两导体球间端点处的电场强度将增加为均匀电场强度的100倍，并用数值计算给出了两球心连线上不同高对称点的场强随不同球心距离时的变化。通过对这一电动力学的经典题目的延伸拓展，使同学增加学习兴趣，并锻炼对计算物理和Matlab计算软件的运用能力。