指南车广义运动方程的创建
2019-09-26邓崇林
邓崇林
(独立研究员)
1 浅谈指南车的来历
指南车这个人造的物理系统是本文的研究对象,想来很多人对此都是一知半解。在本文开始深入探讨之前,先简单回顾指南车的来历。指南车是中国古代的伟大发明之一,也是华夏文化重要遗产之一,在《古今注》及《志林》等中国古籍的记载中,相传四千多年前东方一带的九黎族,为了与炎帝争夺黄河下游地区,为首的首领蚩尤带领九黎族进入中原,并把炎帝赶到涿鹿,于是炎帝向黄帝求救。黄帝联合统帅炎帝等部落,与蚩尤战于涿鹿之野,然而蚩尤善用浓雾,使黄帝的部队迷路陷入险境。黄帝为了克服雾中作战的困难,发明了“指南车”以辨别方向,最终成功突破浓雾的重围,战胜蚩尤,史称“涿鹿之战”,是中国古代历史上一个标志性的重大事件。
指南车乃黄帝与蚩尤之战为破大雾迷阵的一项发明。该车上有一木童,在出发前,令其手指南方,当车启程后,由于车内设有机关,能使该木童手指方向并不随车行进转弯而变,因而有了指向功能,又因其专司指南,又谓“司南”。现代研究者一般皆以齿轮系复原指南车,普遍认为黄帝时代并未发明齿轮,何来指南车,因此传说不可信。虽然传说不可考,但传说并没用一般神话手法讲述涿鹿之战,而是凭借着发明物“指南车”协助作战,言之有物,况且现代已经有人发明了完全没用到齿轮,而是使用了斜面、杠杆与曲轴等很原始的简单机械做出指南车[4],因此,传说是可信的,然而这个问题,应该留给考古学家去伤脑筋。接下来,还是回到指南车有关其运动现象的研究吧。
2 研究动机与方法概要
关于大小近乎零的微型指南车之功能属性,已经由文献[1,2]证得它是一台能够在曲面上遂行向量平行移动的机器,然而这只完成了该车作用在曲面上的定性分析,却没有对其运动现象进行更深入的定量探索。前人遗珠后人拾穗,本研究将加以完善前人阶段性成果,以方程为主体思路,发现在纯滚动下,指向器表征的向量经平行移动后,测地曲率会造成其方向发生偏转现象,进而创建微型指南车之广义运动方程。如将作用曲面退化成平面时,该广义运动方程也随之简并成一般在平面上的运动方程。相较于曲面上广义运动方程的微分形式,其另有对封闭路径积分形式的相位方程,这部分已于文献[3]里推导立论。另,本文末尾会以一般指南车行进在平面上以及在球面纬圆上,进行曲、平面两类不同性质的实验,依此验证理论的正确性。
在进行研究探索之前,除前面提到的纯滚动条件之外,有些前提假设在这里补充说明,本文立论都是基于这些假设。由于本研究乃以运动学为基础分析指南车的运动现象,即把一般指南车视为理想刚体同时不考虑指南车重量、施力、转动惯量、力矩等力的作用,加上文献[4]里所提到有关机械线性组件、车轮直立平面、轮轴与指向器平行于地面运动等诸多约束条件,在进行理想化之后,便能简化让指南车形同刚体的平面运动,而指向器的任意转动,将原本由欧拉角表征的章动、进动和自旋3部分运动,跟着退化只剩自旋。至于行驶在曲面的运动情况,因为微型指南车的大小近乎零,同时也满足前述理想化条件,所以可看成是个带有自旋的质点,又由于这是将平面情况加以推广,因而特称为曲面广义运动,该广义一词并非指广义坐标,其乃借鉴广义相对论名称中的“广义”(general)是也,此外,指南车曲面广义运动还真的与广义相对论有那么一点点微妙关系,其中的平行移动就是它们的共通纽带,而且都会牵涉到弯曲空间里的运动情况,也都要考虑空间退化的议题。
另,由文献[4]指南车控制理论得知,指南车除了有制造上的系统误差之外,它还无法克服车辆行进间地面颠簸或光滑所产生的误差,总之(1)轮打滑则轮多转,从而导致指向精度更差;(2)车跳动则车多转,从而导致转弯精度更差;(3)现实工艺非线性,从而导致构件精度变差等无法消除的三差环节,导致不可能将近似理想化指南车化为现实,换言之,在现实环境下为指南车进行定量实验是没有实质意义的,这也就是为什么一般指南车设计文献并不讨论其定向能力精度的重要因素,因此,本文在第6节中于纬圆上进行的指南车实验,也局限于定性方面的演示,至于定量方面的演示,在不追求精度下可参考文献[3]里的指南车平行动移整合实验仪,它能进行指南车、物理与几何、静态与动态的整合实验,能够实时观察曲面图纸上向量方向与指南车指向器的偏转变化的一次到位整合性实验,并依靠曲面图纸上的向量箭头符号所代表的方位角刻度,能给出指南车指向器的定量角度,后续还会提到。至于要有良好精度的指南车运动量化量测,在现实里是无法实现的,只能靠计算机模拟出精确的向量平行移动,本研究后续也会做出计算机模拟,该动画可在其参考文献中直接执行。
3 曲面上原地打转的微型指南车
今有一紧致定向曲面S,存在弧线元素第一基本形式为:ds2=Edu2+2Fdudv+Gdv2的参数坐标网(u,v),现我们操作一台微型指南车,并利用其能遂行向量平行移动的此一特性,令其纯滚动行驶于前述二维曲面上的局部区域,让车中央划过曲面上一条路径之正则曲线C,且车头方向永远保持与行驶路径相同方向。这就等同于该路径曲线上的切向量,其车架就相当于一个行驶路径上该点的切平面,那么车上指向器就坐落在这个切平面上,而该指向器可看成是此切平面上的单位向量,使得这车平台中央都会接触到行经路径曲线上的一点。那么,此车划过曲线在该点的测地曲率kg可表示为下列克氏符号(Christoffel symbols)相关的Beltrami公式[5-7]
(1)
由于克式符号属曲面的内蕴性质,而上述式(1)测地曲率公式只与克式符号和曲面第一基本形式有关,因此,测地曲率与坐标基底选取无关,实属曲面的内蕴几何量[8]。又该曲面S的度量张量为
(2)

(3)
如果曲面参数化改采正交坐标网,也就当F=0时,则所有克氏符号各分量与第一基本形式的参数关系式如下[10]:
(4)
现令该微型指南车在原地打转Δθ,由于曲面属黎曼流形,流形上每一点的有限邻域不一定是“平”的,然而当这个邻域够小时,是可以当成平面来看,能满足欧氏几何三角形三边的勾股定理,此时的曲面参数坐标网(u,v)在该点之式(1)测地曲率并不会对原地打转的指向器造成影响,所以当车头原地拐角产生Δθ的几何相位变化时,指向器会随之转动Δφ,两者运动关联可表成下列的关系式:
Δφ=-Δθ
(5)
上式等号两边同时对时间微分,则可描述微型指南车的原地补转运动现象,就如同一般指南车在平面上的运转情况,其指向器会以车头旋转方向同时做等量反转,使得指向器方向没变,只有车头在转,这也就是式(5)中负号所起的作用,这在后续探索指南车平面运动时还会深入讨论。
4 创建曲面上指南车的运动方程
当车头停止拐角之后,此微型指南车所在曲面局部区域改采半测地坐标网,则该曲面有第一基本形式为:ds2=du2+Gdv2,且车头将沿着v坐标线行驶,那么沿C曲线行进的指向器向量之各分量ξk必须满足平行移动方程,其分量公式如下所示[11]:
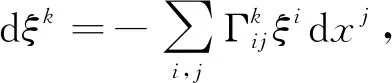
(6)

(7)

(8)
以上推得指向器随路径的方向转变量|dφ/ds|,正是沿该路径各点的测地曲率kg,其负号表示相对于行驶路径偏转的反方向。此外,前述推导虽是基于半测地坐标网以及特定路线的选用,然着实与微分几何专书[12]所得结果殊途同归,同样指出向量在曲线上平行移动时将伴随着方向偏转,且其背后唯一成因是测地曲率。又,该专书是以测地曲率定义结合向量运算方式得到上述式(8)的异曲同工推论,这也额外左证了测地曲率的确是个与坐标选取无关的不变量(invariant)。现把式(5)对时间微分以及将式(8)重新整理得出微型指南车的曲面广义运动方程如下:
(9)
查式(9)之随行运动方程,会发现其运动与所耗时间多寡毫无关联,此时,微型指南车其指向器偏向角随运行路径的微分变量,是完全依据微型指南车行经该曲面路径上的测地曲率来描述其运动现象,这是纯然的几何效应。另查式(9)之拐角运动方程,由于指向器是反车头打转方向进行等量的自旋运动,方向上因车头打转所生的亏角能立即完全得到补偿而不发生变化,保证了其方向固定不变,同时,也可从式(5)知车头原地拐角Δθ时,表示曲线切线方向的几何相位也产生等量变化。
5 创建平面上指南车的运动方程

图1 取自文献[1].B.1.指南车在平面上小转弯示意图
这里暂且撇下方向只看相关量的变化,首先来建立前述(1)、(2)情况与指南车的关联性。由于曲面上曲线的“测地曲率”,是平面曲线其“曲率”的推广[13],反过来说,就是当曲面退化成平面时,测地曲率kg就会变成一般的曲率κ[14]。又由物理直观得知,在同一小段时间内,上述3种情况是同时发生的,而且前两种情况有共同的曲率中心,这同时,指南车车架中央指向器也会自旋δΨ,因此,曲面上的式(9)之随行运动方程也会退化演变成下列平面上中央弧线曲率κ与指南车两轮行程差的关系式:
(10)
以上算式表明中央弧线线素与曲率的乘积,等于一般指南车在平面纯滚动行驶时,其内部机构能将左右轮之行程差变成指向器转角δΨ的证明,这正是那个由车轮直径等于两轮间距又等于2ε所建构而成的Lanchester型指南车机构之运转公式[1]。这有双层意义,第一层表示一般指南车两轮行进划过平面的双轨等距曲线,可以改用由车架中央微型指南车划过平面的单条路径曲线来取代,因此,一般指南车车心与车头连线方向就是该中央曲线的切线方向,换句话说,曲面上退化的随行运动方程是可以描述一般指南车在平面上小转弯的运动现象;第二层则是微型指南车其指向器运动现象,是等同于一般指南车中心之指向器运动现象,都拥有随行转角的共同基因,也就是平面上微型指南车与一般指南车这两者是等效的。余下的问题是,该如何正确描述其指向器转角的运动现象。
现在定义一般指南车右左轮子相对轮轴心的旋转角速度ωi≡d(si/ε)/dt,i=R,L,以及定义θ为车架以车心到车头为准的方向旋转角度,并令指南车以车架中心为圆心做原地旋转一圈行打转动作,又车轮转一圈所走的长度为2Rπ,且两轮间距L=2R=2ε,而车轮转一圈所走的长度刚好是轮车架绕满车心一圈的圆周长(Lπ=2επ)。所以当车轮以轮轴心自转一圈,这同时轮车架也绕车心公转一圈,也就是两者具有完全同步化且相等的角速度,若对时间微分,则有ω=dθ/dt。又由于两侧车轮需反向等量的转速才能原地打转,且令左轮之ωL=ω,那么车架做原地旋转的另一侧右轮角速度则为ωR=-ω,代入式(10),可得指向器转角Ψ与车架原地打转θ的关系式为
(11)
前述是指向器补偿自旋、车轮自转与绕车心圆周运动此3者同步的特征,完全符合实际运动现象,所以车轮以轮轴心自转一圈,同时轮车架绕车心公转一圈,恰好指向器也反向自旋一圈(相对于车架),是同时开始进行也同时绕满一圈之故,其中,轮车架公转与指向器反向自旋刚好相互抵消,使得指南车具有指向不变作用。此处计算是居于车架原地打转的结果,直觉上,式(11)乃是指南车平面运动中的一个特例,我们要问果真是如此吗?是否另有文章,这得继续深究下去寻找答案。
设T(s)是曲线C的单位切向量场,s是弧长参数,用δθ表示向量T(s) 与T(s+δs) 之间微小弧长变化下的微小夹角,也就是车架转向的微转角,又文献[15]对曲率可定为κ(s)=|T′(s)|=|dθ/ds|,它表征着平面曲线的弯曲度,也就是曲率度量了曲线在两邻近点之切向量其间夹角对弧长的变化率。此时将该公式代入到式(9)之随行运动方程同时对时间取微分,可得到退化的随行运动方程式为
(12)
上式原本是将与路经有关的随行运动方程代入运算,结果弧长参数居然消失了,即此运动方程与坐标选取无关,也与路径无关,当然也就与曲率无关。不仅仅如此,连整个方程都与原地打转的式(11)一模一样,于是原本用于曲面上的两个运动方程式(9),若退化成平面,那么将简并为单一个运动方程,现加入方向考虑,也就是,车架打转与指向器自旋是等量反向关系,于是重新整理如下:
(13)

图2 在平面上任意行驶

图3 与任何行经路径无关示意图

图4 原地打转方向不变
上式运动方程表明,等号前面左项之车架转向的角速度dθ/dt与右项之指向器的角速度dΨ/dt等两者之和永远为零,无论指南车运动状态是原地打转或是任意行驶,只要当车架转向产生角速度变量,这同时,其指向器会反车头旋转方向做等量反转的角速度,这两项运动现象叠加起来刚好相互抵消,这样就能让指向器一直保持所指定的方向。从式(13)中可观察到,此运动方程与坐标基底选取无关,也与行驶路径无关,这就是一般指南车在平面上进行任何运动时,其指向器丝毫不受影响并一直保持特定方向的密秘所在。指南车无论在平面上原地打转或任意行驶,基于其自身机械机构的补偿旋转作用[4],让指向器就如同一般向量在欧氏几何平面里任意自由平移,因此特称式(13)为平面上指南车的“自由平移方程”。图2与图4是指南车在平面上任意行驶的实际实验照片,其指向器始终保持固定方向,与任何行经路径无关,就像图3的示意图,其运动与原地打转无异。由于此处物理系统是选取指南车一整体的运动,因而其轮子、机构等运作细节被当成似内力传递般不做表述。
回顾第2节中所说的,在理想化条件下,能简化让指南车形同刚体在平面上的运动,根据运动的叠加原理,刚体平面运动可看成是刚体的平动与转动的叠加,又前述式(12)已证得指南车在平面上的运动完全与选取路径无关;或者,采另外一个观点,由于平面时克氏符号为零,使得直角坐标中平行移动任一向量V的协变导数将缩减成只有一项:dVi/ds=0,这也充分证明了此时的向量平移移动与路径毫无关联,这与图2至图4之指南车平面运动的观察十分吻合,同时也验证了指南车平面运动是其曲面平行移动的特例。以第5节这样分析指南车在平面上的运动现象,就能再次化简成刚体在平面上如式(11)的转动而已,于文献[4]中就是采此条件另用控制理论证明任何一种车轴轮径比例设计的指南车在平面上运动都遵守着式(13)自由平移方程,这是一般认知的经验公式。
6 纬圆上的指南车实验
在这个例子中,我们感兴趣的是微型指南车绕某个闭曲线尤其是在单位球面纬圆作平行移动一周之后,经式(9)之随行运动方程主导下,其指向器所表征的向量方向或几何相位的变化。首先选用球极坐标系(θ,φ),其第一基本形式为:ds2=dθ2+sin2θdφ2,其中θ是极角,与纬度λ的角度变换为:λ=π/2-θ,这使得cosθ=sinλ两者成余角关系,则其度量张量可表成下列关系式:
(14)
由式(14)知E=1,F=0且G=sin2θ,再代入式(4)中便可求得球面上微型指南车式(9)之随行运动方程中测地曲率所需的相关克氏符号系数为
(15)
今微型指南车行经纬圆曲线是沿着v=φ(s) 坐标线,使得u=θ是常数值,那么其测地曲率可从式(3)中化简为
(16)
又,纬圆的弧长元素为ds=sinθdφ,经式(9)之随行运动方程对封闭路径作线积分,就能计算出向量于北纬λ平行移动绕该纬圆一圈后指向器之方向变化量或几何相位如下:
(17)
从理论上推导便知该当如何操作微型指南车,使其指向器向量围绕单连通区域的闭曲线作平行移动,但其微型化在实务上往往并不是那么容易成为现实。所幸球面的对称性与指南车中心相对于两侧双轮具左右对称性,只要指南车相对球面是够小的话,其实这个指南车操作式实验证明是容易实施的。在本文段落下方图5至图9布置了此项实际实验经过照片,正是拿一般指南车置于够大的地球仪上,且车架中心恒对准北纬30°线,只要稳当操作,让指南车纯滚动向东行驶一圈后,可以观察到指南车上头的指向器会顺时钟方向转180°,与前述理论推算值Ψ=-2πsin(30°)完全吻合。另,这个指南车在球面上的操作式实验,也能给出傅科摆摆面进动的理论与实验证明[3]。若在北纬48.8°巴黎做傅科摆实验一天偏转约270°,当然用指南车也能做出同效演示。虽然傅科摆是一种动态的物理系统,综合来看,它确实具有物理与几何更深层的连结,研究[16-19]指出不同纬度傅科摆摆面周期互异,其摆面一天几何相位也是一样同式(17)的数学模式:Ψ=-2πsinλ。另,傅科摆在巴黎展出的第二年,傅科更发明了机械式的陀螺仪来证明地球自转[20],当陀螺仪里的转子高速转动时,由于角动量守恒使其轴永远指向一固定方向,这和傅科摆的摆面向量是相通的,他用希腊字根 gyros(旋转)和scope(看)两字合为“gyroscope”一字来命名这种仪器并沿用至今。

图5 北纬30°开始向东出发

图6 指南车过境美国

图7 指南车快到地中海

图8 指南车经过中国

图9 绕回到原出发处
在前面第2节已经提起过,由于各种无法消除的误差存在,这里只能进行定性方面的演示,至于定量方面的演示,在不追求精度下可参考文献[3]里像图10所示的指南车平移整合实验仪,该图是这个指南车行驶于曲面能观察指向器运动的整合实验视频[21]里记录的一幕,百闻不如一见,相信在观赏该视频之后,会对老祖宗传下来的古科技刮目相看,它居然也能探索曲面空间的新领域。

图10 指南车平移整合实验仪
7 再论平行移动方程与随行运动方程
曲面上操作微型指南车已经能用平行移动方程描述其指向器随行偏转过程,那为何还要多此一举,另行寻找广义运动方程呢?此处会将该理由说个明白。这里沿用前述在单位球面纬圆上向量作平行移动的例子,并且改符号选用了球极坐标系(φ,θ)及第一基本形式为:ds2=dφ2+sin2φdθ2,其中φ是极角,现在要对其平行移动方程进行求解。首先,可以从式(4)中很容易求得与平行移动方程相关且不为零之克氏符号系数有:
(18)
今在极角φ=φ0的纬圆上有任一向量(θ)=(vφ(θ),vθ(θ))进行平行移动,则该纬圆曲线的参数表示式为γ(θ)=(sinφ0cosθ,sinφ0sinθ,cosφ0),那么将该向量套用式(6)平行移动方程可得到下列两个微分方程:
(19)

(20)
接着运用矩阵指数(matrix exponential)技巧套用到式(20)之矩阵方程并求得其解为
(21)
上述式(21)告诉我们新位置向量是通过对初始位置向量经2×2旋转矩阵的一个顺时针旋转所生成的。虽然解出来的这个向量在长度上不同于先前的v(θ)向量,但其顺时针旋转角度却是一致的,也就是说,在极角φ=φ0纬圆曲线上任一点该向量会顺时针旋转且其角度为((cosφ0)θ)。如果初始条件是一个朝南方的单位向量,即vφ(0)=1,vθ(0)=0,代入式(21)将会得到新向量其分量如下:
(22)
今于纬度30° 向东绕一圈θ=2π回到原出发点时,也就是φ0=π/3,((cosφ0)θ)=π,代入式(22)将求得绕一圈回到原出发处之向量变为:vφ(2π)=-1,vθ(2π)=0,这是个朝北方的单位向量,于是我们可以看到如图11所示的单位向量在单位球面纬圆30°向东绕一圈之平行移动的运动图像。
在单位球面向东绕纬圆一圈之同一个问题上,回顾前两个理论计算例子中,前一个运用随行运动方程手法只求得向量顺时针旋转了180°;至于后一个运用平行移动方程手法,从平行移动方程求解中,不仅能与随行运动方程一样求得向量经平行移动回转一圈后发生相同的顺时针旋转角度,另外还能得到向量在纬圆参数曲线上任一点如式(22)的参数表示式,有了这个参数式就能用计算机为其绘制如图11所示的明确图像,这一特点是随行运动方程办不到的。现在该是时候进一步讨论,微型指南车需要怎么样的运动方程。虽说平行运动方程两者都是与坐标选取无关的数学表述,然而从前面探讨得知平行移动方程能带来更多物理内涵的优势,那为何还要额外为其界定广义运动方程呢?这会牵涉到下列7项议题:
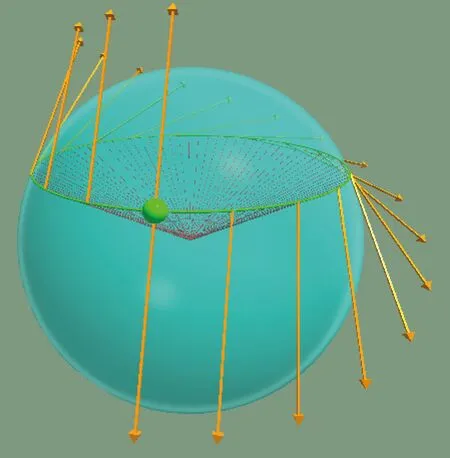
图11 向量在北纬30 度向东平行移动图
(1) 物理系统的运动方程主要是以其物理量作为表征。针对微型指南车这个人造的古典物理系统,当其在曲面上行进运动时,如式(9)所示会带来路径变量与其指向器伴随的角度变量,但平行移动方程并没有涉及到这些直观物理量。
(2) 物理系统的运动方程最好能明确表征造成运动与其作用量的因果关系。式(9)之随行运动方程能表明微型指南车在曲面上其指向器角度的随行偏转运动,其作用量是来自测地曲率,但平行移动方程并无法指出该偏转运动与其成因之间的直接关系。
(3) 物理系统的运动方程最好能有简明的数学形式。很显然,平行移动方程的数学形式要比随行运动方程复杂得多。
(4) 方程能充分表征其对应的物理模型特征。微型指南车在曲面上行进运动,其指向器之角度变量是依赖行经路径的,这个重要特征在平行移动方程里直观上找不到。
(5) 方程能方便带出几何相位。若将微型指南车其指向器之角度视为相位角,由于我们对相位角的绝对值和瞬时值都不感兴趣,至于在曲面上行进运动其始末状态间的相位角偏差量方具有物理意义,然而在求得这个几何相位方面,在前面对平行移动方程探索例子中,要先运用联立微分方程解题技巧求解之后方能得到;反观随行运动方程就简明多了,只要进行相关路经积分就得了。
(6) 运动方程无论在曲面或平面要有直接演绎关联性。式(13)自由平移方程是式(9)曲面广义运动方程跟随作用面退化成平面之后自然衍生而导出的结果,然而当作用曲面退化成平面时,曲面上平行移动方程却无法依作用面退化条件直接演绎成平面上的自由平移方程。
(7) 理论与实验的自洽性。本文从微型指南车在曲面上行驶满足平行移动方程的假设开始,经严谨数理推导出式(9),之后可退化成平面上的式(10),如将该式中行程里的轮半径因子提出来,那将会是个一般指南车的角速度特征公式[4];回头看文献[1]的推导方式则是倒过来的,一开始先把式(10)取微型化推广至曲面,接着用一阶近似方式算得其协变导数为零,证明了微型指南车在曲面上运动乃遂行平行移动,因此,本文与文献[1]相互论证了指南车遂行平行移动的理论自洽性,而且可由式(9)能自然衍生出平面上的式(13)自由平移方程,而式(13)乃传统设计指南车必须遵循的经验公式,这样,理论与实验完全一致自洽。
平行移动方程是微分几何中的一般通用公式,并经文献证明[1,2]可套用解析微型指南车行驶在曲面上的运动现象,然而综观上述分析,就知此方程如要做为微型指南车的运动方程是有所欠缺或针对性不足,因为该方程并不针对微型指南车这个物理系统来表征其运动现象,是个纯数学观点下的产物。至于随行运动方程,则能很好地满足前述7项议题要求,它正是为微型指南车量身订做的微分方程,因此将其纳入式(9)微型指南车广义运动方程里面的一员。
8 结论
看似积木玩具般的指南车,以前觉得它只会木童遥指向南且不随行而偏转,之外,就没别的能耐了,何曾想到,当指南车从平面走向曲面,深入研究发现,竟有如此有趣的运动现象。现总结一下探究其运动规律心得如下:
(1) 指南车保守方向的守恒律。在保守力场且无摩擦力的力学系统下,保守力所做的功可用位能的形式表示,物体运动将遵守着机械能守恒律,其数学关系式表为:ΔE+ΔU=0,其中等号前面左项E为动能而右项U为位能,且这两项总合的总能量始终为零。其实像这样的特征,是具有更为丰富的普遍性,换言之,当一个物理系统有这种不变量的物理内涵,正意味着一种守恒律,例如,平面上的指南车,由于几何空间的平坦对称性以及在纯滚动的力学系统下,其自由平移方程式(13)也有着两项总合为零的特征,在该方程式中,等号前项车架转向θ与后项指向器反其方向偏转Ψ这两项运动现象叠加起来始终相互抵消,使得平面上指南车其指向器保守着方向上的守恒律。
(2) 指南车的几何相位。微型指南车在不考虑力的作用下,若将式(9)之随行运动方程中的左项里分别对分子、分母加入对时间的微分,这样会将原式中指向器偏向角随行驶路径的微分变量,变成是指向器自旋角速度除以车辆动作路径的切线速度,就能得到式(9)新的数学形式,那么运动学物理图像的感觉就复活了,然而这样会顾此失彼,丧失了对该运动现象本质上是纯然几何效应的直观描述,又由于微型指南车每每在曲面相邻两点运动时,其法线方向也随之改变,因此在回到闭合回路的原出发处之前,是无特定基准来衡量其指向器方向的偏转量,因而有意义的观察是让车绕回到原出发处,即从几何观点对运动方程进行封闭路径积分,这已于文献[3]里推导立论,可视为一种对曲面上高斯-博内公式的操作式证明,其结果只呈现几何效应。在前述文献[3]中之式(8),正是本文之式(9)对封闭路径积分与累积拐角的相位方程,其指向器偏向角总量,称之为指南车的几何相位。
(3) 以方程为主体思路。很多微分几何专书能从测地曲率定义切入,运用向量运算,最后推导出向量方向随行偏转变化量与测地曲率的关系式,例如文献[12]。毋庸置疑这些数学家的超强能力,但似乎没能认识到这项公式对指南车的运动有重要意义,其主要障碍应来自两个症结,首先是缺乏跨领域的学习,无法有效地将微分几何知识链接跨越到机械领域的指南车;其次是缺乏以方程为主体的思路,这在量子力学科学史上,就曾发生涅盘般的方程之战。在1925年,瑞士苏黎世每两周会举办一场物理学术研讨会,有次研讨会里,薛定谔做完有关德布罗意波粒二象性的报告后,德拜(Peter Debye)指出,既然粒子具有波动性,应该有一种能够作为表征的波动方程式。薛定谔深受这种以方程为主体思路的引领,很快地,在下一轮研讨会中,薛定谔就提出了量子力学的波动方程[22]。本文乃以方程为主体思路,先是从“平行移动方程”切入,发现指向器表征的向量经平行移动后其方向会产生偏转现象,并找到造成方向偏转的原因是测地曲率,进而创建微型指南车之广义运动方程。
(4) 古代指南车的新时代诠释。本文以黎曼几何切入讨论了指南车在弯曲空间的平行移动特性,这些都不是古人能够想到,或者总结出来的。不仅如此,这也创新突破了用复原或复兴诉求进行指南车的研究,更把英国学者李约瑟对指南车的研究[23]带到全新篇章,本研究重新发现其曲面运动规律之奥妙,而一般对指南车所认知的平面运动,只是其曲面运动规律退化后的特例。
(5) 应该是首次用微分几何为中国古科技创建数理模型。对于学习或研究非欧氏空间例如微分几何、广义相对论或量子物理的相位因子等等的初学者而言,由于那些纯然数学符号充满高度抽象且艰涩难懂,很难有具体化的感觉,让人望而生畏。一般会借助计算机绘图帮助建立平行移动概念,本研究也做出计算机模拟,其源码放在参考文献[24]中,执行结果如图11所示,它虽是动态演示,然而却无法与指南车相比,因为指南车恰好提供一种手脑并用效果,只要动手做,能很快地把非常抽象的数理概念予以具体化,这对学习效果大有帮助,对前沿研究的养成教育亦有帮助,也提供看问题的多元角度,并有助提升中高等自然科学教育。
(6) 本文视指南车内在运作机理为黑箱。本文乃研究指南车外在的运动规律,至于其内在运作机理则视为黑箱,已与本文做了切割。关于指南车内在运作机理的探讨,将于文献[4]做进一步的研究。
