李普曼-史温格方程在耦合道中的应用
2019-09-26宋开兰刘利娟李德民
王 恩 宋开兰 刘利娟 马 冰 李德民
(郑州大学物理工程学院,河南 郑州 450001)
1 导出问题
强子之间的相互作用以及强子性质是强子物理领域的重要研究对象,基于强相互作用的规范理论——量子色动力学(Quantum Chromodynamics,QCD)理论发展了很多研究强相互作用的唯象理论。其中,手征微扰理论系统考虑了手征对称性及其自发对称性破缺,可以成功的用于描述最轻的赝标介子之间相互作用,然而,由于该理论中拉氏量是对动量和质量微扰展开,因此并不能直接用于描述共振态的性质。手征幺正方法从手征微扰论得到的振幅出发,利用耦合道的李普曼-史温格(Lipmann-Schwinger,L-S)方程来描述无穷多s道散射圈图[1,2]。手征幺正方法在解释和预言强子共振态的动力学性质方面取得了很多成功[1-4]。例如,手征幺正方法预言在Λ(1405)共振态质量附近有两个非常靠近的极点,这也被大量实验所证实,相关讨论可以参考粒子数据组(Particle Data Group, PDG)关于Λ(1405)共振态的综述介绍[5]。

本文结构如下,首先在第2节从希尔伯特空间定态散射过程导出L-S方程,然后在第3节将L-S方程推广到耦合道情况,并导出B-S方程,第4节并讨论了Λ(1405)的双极点结构,最后为本文的一个总结。
2 定态散射过程中李普曼-史温格方程
对于两粒子的散射过程,入射粒子受到散射中心的作用,其相互作用可以用势场V(r)描述。在实际散射过程中,势场一般是连续且光滑的,在r→∞时,势场很快趋于零。 当势场V(r)不随时间变化时,由于入射粒子具有确定的动量p,散射过程中能量是守恒量,这便是定态散射[6]。
在希尔伯特空间中,入射平面波φ满足的薛定谔方程为
H0|φ〉=E|φ〉
(1)
其中,H0为入射粒子的哈密顿算符;E为入射粒子的能量。描述定态散射过程的薛定谔方程为
[H0+V(r)]|ψ〉=E|ψ〉
(2)
其中ψ为定态散射波函数。式(2)减式(1),得到
[E-H0]|ψ-φ〉=V|ψ〉
(3)
为了求解该方程,需要将逆算符1/(E-H0)作用于方程两边,可以得到
(4)
需要注意的是,这里假设了逆算符1/(E-H0)是存在的。一般情况下,算符H0的函数也是算符,其本征矢可以由算符H0的本征矢定义,即
f(H0)|Ei〉=f(Ei)|Ei〉
(5)
由于逆算符1/(E-H0)在H0的本征态φ上会出现奇点,为了解决这个问题,将能量Ei扩大到复数域上,即式(4)可以改写为
(6)
其中ε为一个无穷小量,在全部运算完毕后再取ε→0极限。原则上ε前面的符号可正可负。当ε前面符号为正时,格林算符为推迟格林算符,表示较早时刻的态对当前态的影响;当ε前面符号为负时,格林算符为超前格林算符,表示未来的态对当前的态的影响,即超前格林算符没有物理意义[6]。其中将能量Ei扩大到复数域上的逆算符为格林算符,即
(7)
式(6)即为李普曼-史温格(Lipmann-Schwinger,L-S)方程,该方程是与式(2)的定态散射的薛定谔方程完全等价。
为了将散射振幅表示为算符的矩阵元,定义算符T,满足
T|φ〉=V|ψ〉
(8)
T算符又称为跃迁算符。将势能V作用于式(4)两边,并利用式(7)可以得到
(9)
由上式可以得到算符满足的关系为
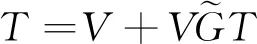
(10)
将上式中算符T进行迭代,有

(11)
该式为T算符的波恩级数,其对应无穷多s道散射过程。当散射势能远小于哈密顿H0时,上式右边的后一项远小于前一项。由右边第一项算出的截面为一级波恩近似,由右边前两项算出的截面为二级玻恩近似。
3 L -S方程在耦合道中的应用

(12)
结合式(10),可以得到散射振幅在相应耦合道中的矩阵元为

另外,公式(13)~(15)也可以表示为如下矩阵方程,
(16)
上式中第二项包含了对四动量q的积分(这里是在相对论框架下进行讨论的),
(17)
上式中k,p为散射过程中初态耦合道中两个介子的四动量;k′和p′分别为末态耦合道中两个介子的四动量。一般情况下,在计算式(17)中的积分时,矩阵元v和t均不在壳。不在壳部分的散射振幅的结构与树图振幅的结构相似,因此在实际的计算过程中,将不在壳部分的贡献吸收到树图中,所以可以取矩阵元v和t都在壳[4],这时式(17)可以简化为
(18)
式(16)描述的耦合道散射过程可以用图1表示。图1(a)对应耦合道之间的散射振幅t;图1(b)对应式(16)右侧第一项所示的耦合道之间的相互作用势v;图1(c)对应于式(16)右侧第二项的vGt(或vijGjjtjk),其中矩阵元Gjj对应于第j个耦合道中两个介子的圈图传播子,vijGjjtjk表示第i个耦合道中的介子对通过相互作用势vij首先散射到作为中间态的第j个耦合道的介子对,之后再通过tjk转化为作为末态的第k个耦合道的介子对。当把式(16)右边的散射振福t进行迭代,就可以得到,
(19)
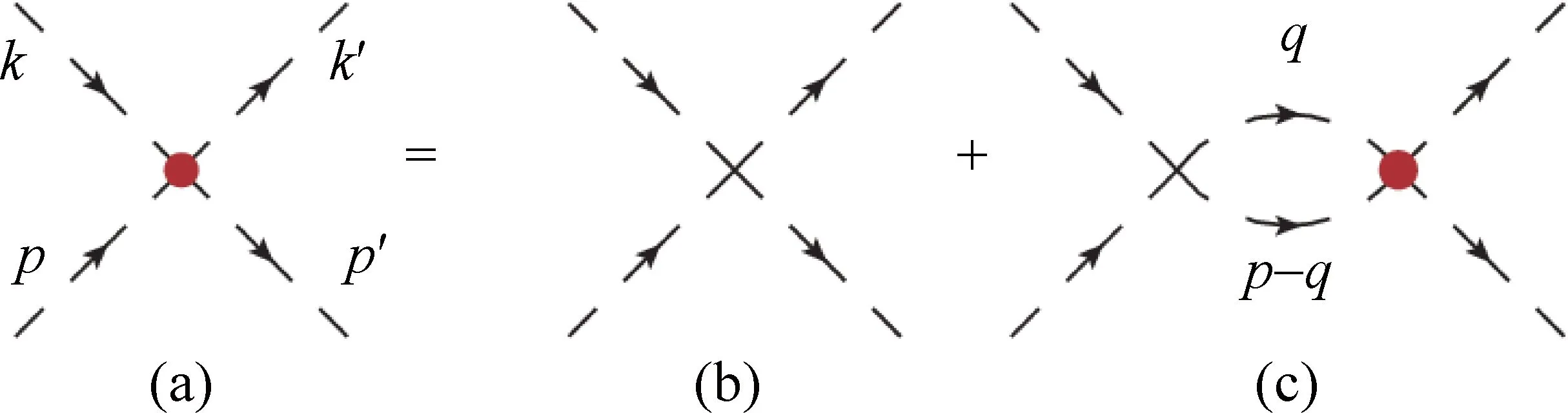
图1 耦合道的散射过程
上式右侧第n(n>1)项,代表包含n-1个s道散射圈图的贡献,即初态耦合道中的介子对通过n-1次重散射转化为末态耦合道中的介子对。
需要注意的是式(17)和(18)中的矩阵元Gjj不再是由式(7)描述的格林算符给出的矩阵元,而是相对论情况下耦合道中两个介子的圈图传播子[4],由量子场论可得
(20)
式中,P为介子-介子耦合道系统的总的四动量;q为圈图中其中一个介子的四动量。
(21)
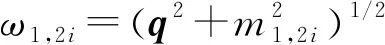
将矩阵元v和t提到动量积分外面,由式(16)可以计算出散射振幅为
(22)
上式即为耦合道的L-S方程,又称为Bethe-Salpeter方程。

(23)
在某些情况下,散射振幅第一黎曼面上会有实的极点,这对应于动力学产生的束缚态(1)此处所谓的束缚态,指的是其质量小于最低耦合道的阈值的态。。这些动力学产生的共振态与第i个耦合道的耦合常数gi可以通过计算散射振幅在极点位置的留数得到,即
(24)
一般来说耦合常数gi为复数。
4 Λ(1405)的双极点结构
本节将从赝标介子和最低质量的八重态重子出发,利用B-S方程计算Λ(1405)的双极点结构。首先,包含八重态赝标介子和JP=1/2+八重态重子的最低阶相互作用拉氏量为[2]
(25)
符号〈〉代表对矩阵求迹,f为耦合常数,f=1.15fπ,fπ=92.4 MeV[2,7]。其中Φ和B分别为介子和重子的SU(3)矩阵元,
(26)
由式(25)可得到耦合道之间的最低阶的相互作用势能,
(27)
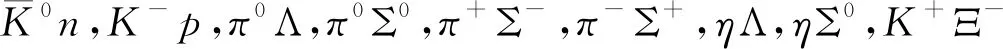
(28)
Mi和Ei分别为第i个耦合道中重子的质量和能量。

(29)
(30)
对于式(20)表示的圈图传播子,此处我们采用维数正规化的解析表达式[7],即,
(31)
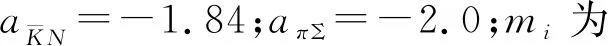
(32)


图和πΣ→πΣ的散射振幅的模方
5 结语
手征幺正方法是从最低阶的手征微扰理论得到的振幅出发,利用推广到耦合道的李普曼史温格方程来描述无穷多个s道散射圈图,手征幺正方法在描述强子共振态的性质方面取得了成功。本文中,我们从希尔伯特空间的定态散射过程出发,首先介绍了李普曼-史温格方程,然后推广到耦合道的散射过程,并得到计算耦合道的散射振幅的Bethe-Salpeter方程,并介绍了散射振幅的极点与共振态的对应关系。最后,我们利用计算耦合道散射振幅的B-S方程计算了Λ(1405)的双极点结构。
