对一道练习题的多解思考及教学展望

刘春云

[摘  要] 如何把一道题讲透，真正体现该题应有的价值，需要教师在课堂上让各种个性化的解题方法一一呈现. 不仅如此，教师还应在解题教学之后，引导学生总结几何模型，总结经验得失，逐步提高学生的数学素养和数学能力.

[关键词] 练习题;多解思考;解题教学

很多教师都有过这样的经历：受到某种启示后，引起教学反思，产生教学顿悟，从而促进教学改进. 近期，笔者对一道有关圆的练习题进行讲评时，发现学生中出现了多种解法，而且有不同解法的同学都非常积极地想与大家分享自己的“高见”. 见同学们热情高涨，笔者索性留时间让他们尽情发挥. 尽管原计划讲评的内容没有完成，但课后想想，本节课的收获还是满满的，而且对今后的教学也有了进一步的展望.

题目呈现

解法展示与思考

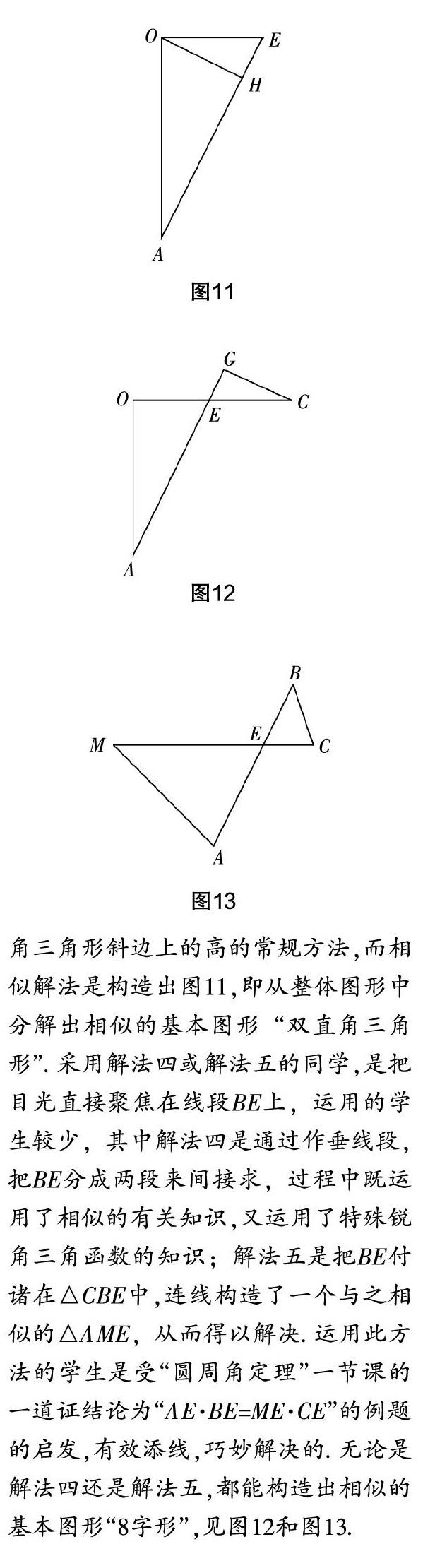
思考  解法一、解法二和解法三均是把AB作为一个整体，先求线段AB，再求线段BE，这是绝大部分学生采用的方法. 其中解法一和解法二是把线段AB作为三角形的边，通过寻找（或连线构造）一对相似三角形来求解. 解法一是从复杂图形中分解出图9，即相似中的基本图形“母子三角形”;解法二是构造出图10，即相似中的基本图形“斜交相似”;而解法三是利用垂径定理来求弦AB，这里又可以用等积法或相似三角形的性质来解决，其中等积法是求直角三角形斜边上的高的常规方法，而相似解法是构造出图11，即从整体图形中分解出相似的基本图形“双直角三角形”. 采用解法四或解法五的同学，是把目光直接聚焦在线段BE上，运用的学生较少，其中解法四是通过作垂线段，把BE分成两段来间接求，过程中既运用了相似的有关知识，又运用了特殊锐角三角函数的知识;解法五是把BE付诸在△CBE中，连线构造了一个与之相似的△AME，从而得以解决. 运用此方法的学生是受“圆周角定理”一节课的一道证结论为“AE·BE=ME·CE”的例题的启发，有效添线，巧妙解决的. 无论是解法四还是解法五，都能构造出相似的基本图形“8字形”，见图12和图13.

教学展望

1. “几何图形到几何模型的抽象”是几何教学的常规思路

几何问题的研究离不开对几何模型的抽象和提炼，而几何模型掌握得越多，解决数学问题的方法和途径也就越丰富. 这就要求我们一线教师在平时的教学中，要不断地引导学生自主经历抽取几何模型、运用几何模型的过程，并鼓励每位学生凸显自己的特点，形成属于自己的几何模型. 该题中，我们可以抽象出的几何模型有：勾股定理、等腰直角三角形、“三角形中已知两边及一特殊角，可以求其余线段”、相似基本图形中的“母子三角形”“斜交相似”“双直角三角形”“8字形”、利用垂径定理求弦长、等积法求直角三角形斜边上的高、相交弦定理（尽管此说法没跟学生提，但结论可以引导学生熟记）.

2. “几何直观到几何推理的过渡”是几何教学的关键过程

相似是几何中非常重要的一类解题工具，它能跟圆、直角三角形、函数、动点、类比探究等问题相结合，出现在中考压轴题中，考查学生综合运用知识的能力. 而且，物理光学、力学的学习，实际生活中的很多地方（如测量、绘图等）也需要用到相似这一工具，其重要性可见一斑. 本题不是压轴题，若相似基础打得扎实，解决起来还是轻而易举的，也就不会出现班级中少部分学生对第（2）问无从下手的现象. 因此，今后教学“相似三角形”这章时，教师还是应放慢脚步，帮学生踏踏实实地把相似的基础夯实. 相似是全等的拓展与延伸，从全等三角形到相似三角形，是一个从特殊到一般的过程，也是学生认识上的一个飞跃. 全等三角形因为图形大小一样，从直观上也能猜出个大概，而相似三角形则不同，从直观上不容易看出来，需要借助空间想象能力，再通过逻辑推理才能证明出来. 从这个角度来说，初中数学教师应在学生能力的培养上舍得花时间、下功夫，要着重培养学生的空间想象能力和逻辑推理能力，这也会为学生今后高中学习立体几何知识打下良好的基础，实现初高中知识的有效衔接.

3. “分析问题本质到提炼解题通法”是解题教学的基本策略

在本题的几种不同解法中，我们可以看到问题的切入点不尽相同，为了求某条线段的长，有的直接求，有的间接求（或由两线段之差得到，或由两线段之和得到）. 但是，纵观以上多种解法，尽管方法多种多样、精彩纷呈，但究其本质，都离不开一个宗旨：线段是三角形的基本元素，要求线段，必先构造三角形. 因此，在解题教学中，教師应引导学生在总结方法的过程中，揭示问题的本质，提炼解题的通法.

4. “多视角思考到最优化解决方案”是解题教学的高效手段

多视角思考、多途径解决问题，可以拓宽学生的思路，培养学生思维的发散性和融合性，使学生的思维，角度更多，范围更广. 从不同角度思考解题方案，既能挖掘学生的潜能，使课堂气氛热烈，又能增强学生的合作学习意识，还可以总结出更加简洁的解题方案. 长此以往，定可以让学生的思维向最优路径收敛. 在不断的经验积累中，学生能逐步提高数学素养和数学能力，解题教学也会从有效走向高效.