基于匹配稳态随机共振的轴承故障诊断方法

2019-09-23康建设张星辉杨志远

复杂系统与复杂性科学 2019年2期

池阔，康建设，张星辉，杨志远，赵斐，2

(1.陆军工程大学石家庄校区，石家庄 050000；2.东北大学工商管理学院，沈阳 110819)

0 引言

轴承广泛用于旋转机械，用于支撑转轴等旋转部件。其故障常导致设备停机，造成巨大的经济损失，甚至导致人员伤亡。越早发现轴承故障，就能越早维修设备，避免不必要的损失。轴承故障诱导产生的冲击信号相对微弱、噪声背景较强、振动传播路径较远等原因导致很难及时准确地诊断轴承故障状态。为准确诊断轴承故障，相关研究逐步展开。Laha[1]将图像处理中常用的局部均值降噪方法拓展到1维信号处理，并通过最大化轴承振动信号的峭度值，确定改进的局部均值降噪方法的各参数。张星辉等[2]采用窄带干扰消除方法，提取轴承振动信号中的周期冲击成分，以判断轴承健康状态。Bessous等[3]采用离散小波变换分析电机电流变化特征，以诊断电机中的轴承健康状态。考虑到轴承故障诱导所产生的冲击十分微弱，需要进一步改进现有研究方法，提高弱故障条件下的轴承故障诊断的准确性。

随机共振(Stochastic Resonance，SR)是一种利用噪声增强微弱信号的特殊物理现象。随机共振认为在特殊条件下噪声信号不仅无害反而有利，适用于强噪声背景下的弱信号探测。随机共振提出后，就开始被应用于各个领域，如信号传输[4]、能量收集[5]、图像处理[6]等。根据绝热近似理论，传统的随机共振只能处理小参数信号(噪声强度D<<1、驱动信号幅值A<<1、驱动信号角频率ω0<<克莱莫斯跃迁率)。然而，工程实际中所采集的信号通常为大参数信号，不能满足小参数限制条件。为解决该问题，大参数随机共振方法应运而生，如变步长随机共振[7]、归一化随机共振[8]、基于频域信息交换和变尺度的随机共振[9]等。这些方法通常将大参数信号转化为小参数信号或改变非线性系统参数，以满足小参数限制条件。

自从大参数随机共振提出后，随机共振逐步应用于机械故障诊断。陆思良等[10]从经典随机共振、改进随机共振和随机共振在旋转机械的应用等3个方面，对随机共振在机械故障诊断领域中的应用研究展开综述。李继猛等[11]将时延反馈单稳态随机共振和自适应最小熵反卷积相结合，用于轴承的故障诊断。池阔等[12]提出基于布谷鸟搜索算法的自适应双稳态随机共振方法，用于轴承的故障诊断。时培明等[13]提出基于时延反馈三稳态随机共振方法，用于旋转机械的故障诊断。然而，目前基于随机共振的故障诊断方法主要集中在单稳态、双稳态或三稳态随机共振。这些随机共振方法的势函数结构单一且所含势阱数量固定不变，既不适宜从复杂多样的机械振动信号中提取微弱的故障特征信号，也不利于实现振动信号和势函数的最佳协同效果。为了丰富势函数的结构，构造了一种新势函数，即匹配稳态势函数。匹配稳态势函数的结构多样，所含的势阱数量可变且由势函数参数C决定。为使势函数与机械振动信号达到最佳协同效果，以最大化匹配稳态随机共振输出信噪比为目标构造目标函数，并采用布谷鸟搜索算法搜索最佳随机共振参数和输出信噪比。相比单稳态、双稳态和三稳态随机共振，所提匹配稳态随机共振具有如下优势：1)匹配稳态随机共振势函数的势阱数量能够根据所输入的机械振动信号进行最优匹配，有利于实现从复杂多样的机械振动信号中增强微弱的轴承故障特征频率信号；2)采用布谷鸟搜索算法自适应地改变匹配稳态随机共振参数，有利于使机械振动信号和势函数协同效果达到最优。

本文在分析匹配稳态势函数的基础上，提出基于匹配稳态随机共振的轴承故障诊断方法，建立相应的故障诊断框架。通过数值仿真，分析匹配稳态随机共振各参数对输出信噪比的影响，对比稳态匹配随机共振和双稳态随机共振的抗噪鲁棒性。通过轴承内圈故障案例和滚动体故障案例，对比双稳态随机共振和匹配稳态随机共振的应用效果，验证所提方法可行性和有效性。

1 匹配稳态随机共振

随机共振(Stochastic Resonance，SR)可表述为：在非线性系统中，微弱信号和噪声信号协同作用下，使得微弱信号显著增强的现象，可用如下朗之万方程(Langevin Equation，LE)进行描述：

(1)

其中，x为粒子运动轨迹；S(t)=A0sin(2πfdt)为微弱驱动信号(驱动频率为fd，幅值为A0)；Γ(t)=(2D)1/2ε(t)为高斯白噪声(Gaussian White Noise，GWN)，D为噪声强度，ε(t)为标准GWN(均值为0，方差为1)；U(x)为非线性势函数。

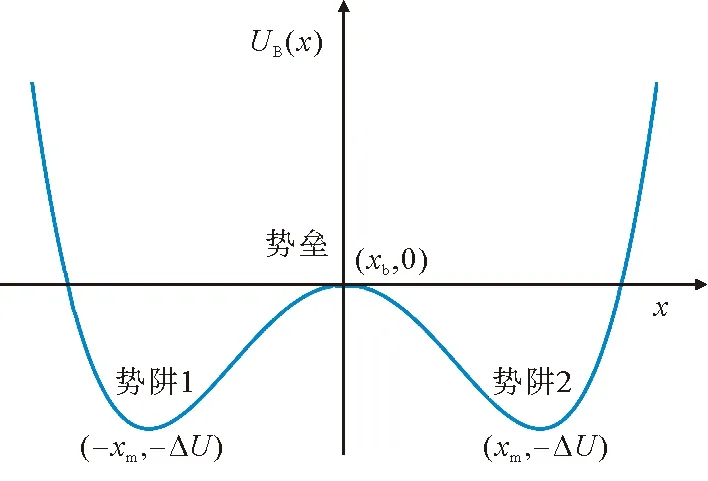
图1 双稳态势函数形状示意图Fig.1 Shape of the bi-stable potential

1.1 双稳态随机共振

双稳态随机共振(Bi-Stable Stochastic Resonance，BSR)是最经典的随机共振，其势函数为双稳态势函数UB(x)，可表示为

(2)

其中，a和b为双稳态势函数的参数，且a∈R+、b∈R+。UB(x)形状如图1所示。显然，UB(x)具有两个势阱(极小值)和一个势垒(极大值)，且xm=(a/b)1/2、ΔU=a2/(4b)、xb=0。

那么，将式(2)代入式(1)，得双稳态随机共振的LE为

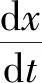
(3)

当驱动信号幅值A0较小时，BSR的输出为[14]

(4)

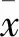
BSR输出幅值越大，则随机共振对驱动信号S(t)的提升效果越好。工程实际中所采集的信号为离散信号。对于离散信号，式(3)可采用Runge-Kutta法求解[12]。令(a,b)=1、A0=0.3，采用5阶Runge-Kutta法求解式(3)，得到不同驱动频率fd下的BSR输出幅值随噪声强度D变化关系，如图2所示。随噪声强度增加，BSR输出幅值先增加再达到极大值后下降，且极大值远远大于驱动信号幅值A0=0.3。因此，当非线性系统固定时，合适的噪声强度能够极大地提升BSR输出幅值。这意味着，在一些特殊条件下，噪声不仅无害反而有益。同时，随驱动频率fd降低，BSR输出的最大幅值明显增加，故BSR更适合提升低频信号。

1.2 匹配稳态随机共振

1.2.1 匹配稳态随机共振

匹配稳态随机共振(Matched-stable Stochastic Resonance，MSR)的势函数UM(x)为

(5)

其中，c∈(-∞,xm]为稳态决定参数；a和b含义与式(2)相同；O为无穷小量。显然，匹配稳态势函数UM(x)由UM1(x)和UM2(x)共同组成。UM2(x)为圆心为(0,B)、半径为R的过渡小圆弧。圆弧UM2(x)与UM1(x)在|x|=O处相交，且交点处切线相同，即：

(6)

匹配势函数UM(x)的势阱数量由参数c决定。若c∈(-∞, -xm]，则UM(x)仅有1个势阱；若c∈(-xm, 0]，则UM(x)有2个势阱；若c∈(0,xm]，则UM(x)有3个势阱。当(a,b)=(1, 1)、c=[-1, 0, 1]时，UM(x)的形状如图3所示。

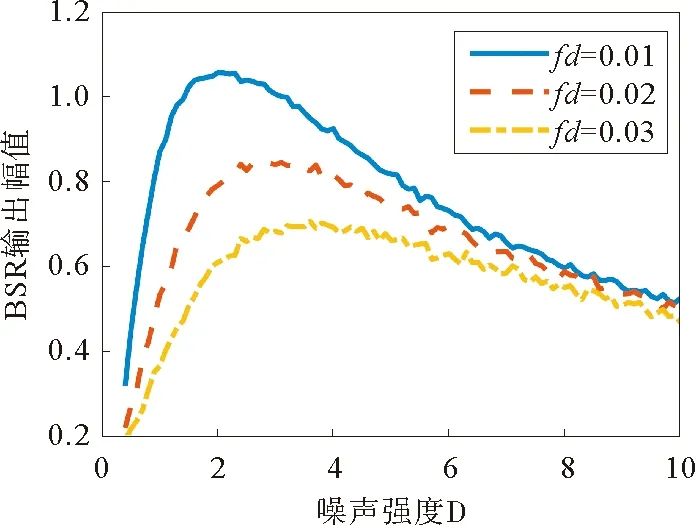
图2 不同驱动频率fd下的BSR输出幅值随噪声强度D变化关系Fig.2 Amplitude of BSR output vs. noise intensity D under different driving frequencies fd

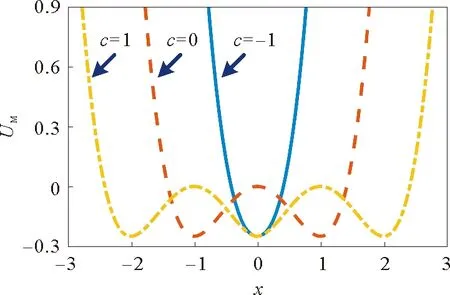
图3 匹配稳态势函数的形状Fig.3 Shapes of the matched-stable potentials

将式(5)代入式(1)，得匹配稳态随机共振的LE：

(7)

其中，

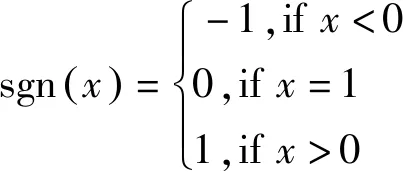
(8)

令z=(b/a)1/2x、τ=at，则式(7)可转换为

(9)

其中，C=c(b/a)1/2∈(-∞, 1]为稳态决定参数；K=(b/a)1/2为幅值增益。经变换后，参数a和b均转换为常数1，参数C取值上限变为1，故称该变换为类归一化变换。经类归一化变换后，驱动信号频率缩小了a倍，幅值扩大了K倍。因此，类归一化变换能够将驱动信号转化为小参数信号，以满足随机共振的小参数限制。

1.2.2 数值实施方法和随机共振输出评价指标

1) 数值实施方法

工程采集的信号多为离散信号s(n)，且为驱动信号S(n)和噪声信号Γ(n)的叠加。令s=S+Γ，采用5阶Runge-Kutta法求解式(9):

(10)

其中，H=a/fs表示积分步长，fs为采样频率。显然，当输入信号s固定时，参数(C,H,K)的取值严重影响随机共振的输出z。

2) 随机共振输出评价指标

目前，用随机共振输出评价指标有很多。这些评价指标可分为两类：第一类为需预知驱动频率的评价指标，如信噪比[13]、局部信噪比[12]、加权信噪比[15]等；第二类为不需预知驱动频率的评价指标，如近似熵[7]、加权功率谱峭度[16]、MPSK指标[11]、综合定量指标[17]等。本文采用最常见的信噪比(Signal-to-Noise Ratio，SNR)作为随机共振输出评价指标，其定义为

(11)

其中，Ad和An分别为驱动信号和噪声信号的功率。SNR越大，随机共振输出z越好。因此，可建立搜索最优参数(C,H,K)的目标函数

(C,H,K)=arg max[SNR(z)]

(12)

1.3 布谷鸟搜索算法

布谷鸟搜索算法(Cuckoo Search，CS)是Yang[18]提出的一种启发式群智能优化算法，具有良好的全局寻优能力，已应用于参数估计[19]、图像降噪[20]、信号处理[12]等研究。本文将采用CS算法搜索式(12)的最优参数和最优值。下面简要介绍CS。

CS模拟了布谷鸟寄生繁衍策略。它将参数取值范围视为整个搜索空间，将参数的取值(即解决方案)视为布谷鸟蛋(或鸟巢)，将目标函数值视为布谷鸟蛋的适应度。对于最大化问题，目标函数值(适应度)越大，解决方案(布谷鸟蛋)就越好。为简单有效地模拟布谷鸟寄生繁衍策略，CS假定了3种理想条件：

1)布谷鸟每次仅产下一个蛋，随机置于一个鸟巢中；

2)最优质的布谷鸟蛋将保留至下一代；

3)鸟巢(布谷鸟蛋)的数量是固定的，布谷鸟蛋以概率Pa∈(0,1)被寄主鸟发现。一旦布谷鸟蛋被发现，该布谷鸟蛋将被寄主鸟丢弃，新的布谷鸟蛋将随机生成。

CS包含了3项重要操作，即候选种群产生、择优选择和随机迁移。下面分别介绍这3项重要操作。

1)候选种群产生

(13)

2)择优选择

择优选择通过比较父体与其候选子代的适应度，保留适应度到下一代。对于最大化问题，择优选择可表示为

(14)

其中，f(·)为适应度函数。择优选择采用了贪婪策略，是第2条理想假设的实现。该操作不仅有效防止迭代过程中反生退化现象，而且加快适应度收敛速度。

3)随机迁移

解决方案以概率Pa∈(0,1)被随机迁移。随机迁移操作可表示为

(15)

其中，xi,j和yi,j分别为迁移前和迁移后第i个解决方案的第j个参数；xp,j和xq,j分别为为迁移前第p个和第q个解决方案的第j个参数，p和q均为随机正整数；w和o均为服从(0, 1)均匀分布的随机数。随机迁移体现了第3条理想假设，增加了种群多样性，降低了种群早熟概率。

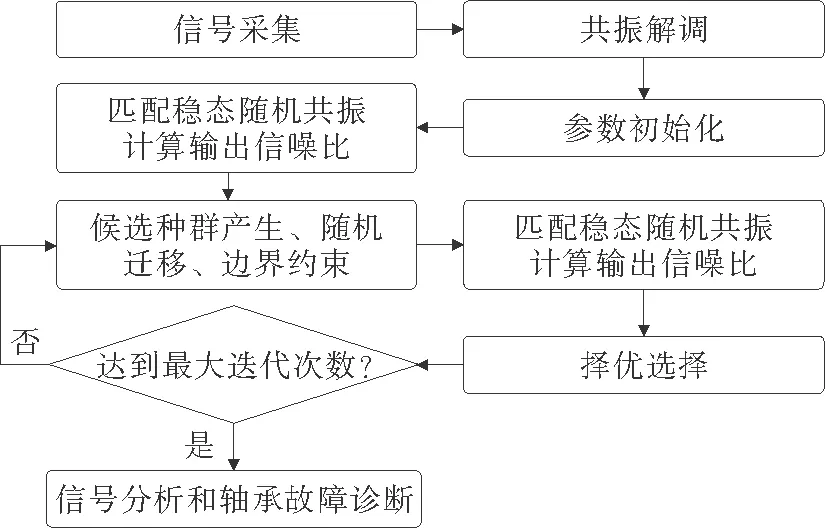
图4 基于匹配稳态随机共振的轴承故障诊断框架Fig.4 Bearing fault diagnosis framework based on MSR

1.4 基于匹配稳态随机共振的轴承故障诊断框架

建立基于稳态匹配随机共振的轴承故障诊断框架如图4所示，具体步骤如下：

1)信号的采集和预处理。采集轴承匀速运转条件下的振动加速度信号s(n)，用高通滤波器滤除所采信号s(n)中的低频成分，用希尔伯特变换求取包络信号se(n)，计算轴承故障特征频率，采用谱编辑技术消除包络信号se(n)中低于故障特征频率且功率谱幅值较高的频率成分。

2)参数初始化。设置参数(C,H,K)的取值范围、种群数量n、最大迭代次数Gmax、n个解决方案初始值(记为A)，步长尺度R、常数β、随机迁移概率Pa等参数，令迭代计数G=1。

3)匹配稳态随机共振和信噪比计算。根据式(10)求解各初始解决方案A的匹配稳态随机共振输出z，然后根据式(11)和轴承故障特征频率计算各输出的信噪比。

4)候选种群产生、随机迁移和边界约束。根据式(13)和解决方案A产生候选种群，根据式(15)对候选种群进行随机迁移，得到候选解决方案B。若解决方案B中的某参数超出所设置参数取值范围，则随机生成取值范围内参数值，替代B中该参数。

5)匹配稳态随机共振和信噪比计算。根据式(10)求解各初始解决方案B的匹配稳态随机共振输出z，然后根据式(11)和轴承故障特征频率计算各输出的信噪比。

6)择优选择。根据式(14)逐一对比解决方案A和B的信噪比，保留信噪比较高的解决方案(记为A)，记录当前最佳解决方案、最佳随机共振输出和最佳信噪比，令G=G+1。

7)判断是否结束。若G≤Gmax，则跳至步骤4)；否则，输出最佳解决方案、最佳随机共振输出和最佳信噪比。

8)信号分析和轴承故障诊断。分析最优随机共振输出的功率谱，判断轴承健康状态。

2 参数分析和抗噪鲁棒性分析

本节通过仿真试验，分析MSR参数对输出的影响和MSR的抗噪鲁棒性。在所有仿真试验中，驱动信号S(t)为正弦信号，噪声信号Γ(t)为高斯白噪声，采样频率fs为104Hz，信号长度N为3 000。

2.1 参数分析

参数分析对确定MSR各参数对MSR输出影响具有重要意义。下面通过数值仿真分析各参数对MSR输出SNR的影响。令正弦信号幅值A0为1，频率fd为50Hz；高斯白噪声强度D为1；输入信号的理论SNR为-6.021dB。为降低输出SNR随机性的影响，各仿真重复50次，计算每次MSR输出SNR，取均值作为最终结果。绘制MSR输出SNR随各参数的变化曲线，如图5所示。

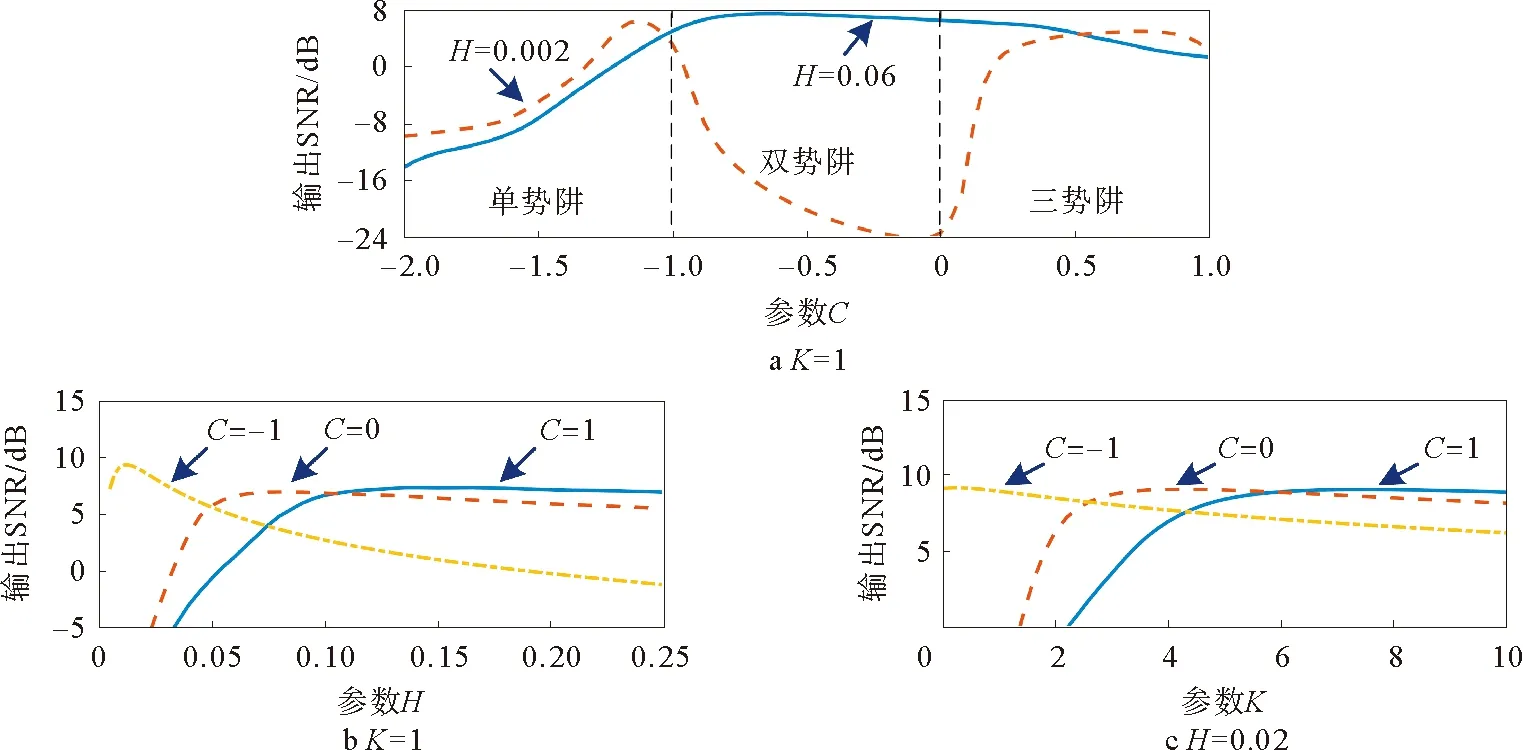
图5 MSR各参数对输出SNR的影响分析Fig.5 Influence analysis of every MSR parameter on output SNR

由图5a可知，(1)当参数H=0.002时，随着参数C增加，MSR输出SNR先增加、后降低、再增加、最后降低。此时，在单势阱和三势阱状态下，MSR输出SNR存在极大值；在双势阱状态下，存在极小值。(2)当参数H=0.06时，随着参数C增加，MSR输出SNR先增加、后降低。在双势阱状态下，存在极大值。因此，参数C严重影响MSR输出SNR，但同时受到其他参数的制约。由图5b(或5c)可知，随着参数H(或K)的增加，MSR输出SNR先增加至极大值、后降低。因此，参数H和K也严重影响MSR输出SNR。综上，想要达到最优MSR输出SNR，应当同时调节参数(C,H,K)。

2.2 抗噪鲁棒性

抗噪鲁棒性反映了MSR抵抗不同强度噪声的能力。令正弦信号幅值A0为1，频率fd为50Hz；高斯白噪声强度D从0.4递增至10(步长为0.4)。采用布谷鸟搜索算法搜索满足式(12)的最优MSR参数，记录MSR输出的最大SNR。每项试验重复40次，取输出最大SNR的均值，作为最终结果。同时分析BSR的抗噪鲁棒性，作为MSR的对比。绘制抗噪鲁棒性分析结果，如图6所示。

图6 MSR和BSR的抗噪鲁棒性对比Fig.6 Comparison of the anti-noise robustness between MSR and BSR

由图6a可知，随噪声强度D增加，BSR和MSR的输出SNR逐渐降低，即抗噪能力逐渐减弱。BSR和MSR的输出SNR均远远大于输入SNR，故SR能够显著提升微弱信号。由图6b可知，MSR输出SNR总是大于BSR输出SNR，故MSR抗噪鲁棒性优于BSR。值得注意的是，当噪声强度D大于2后，随噪声强度增加，ΔSNR呈现递增趋势。也就是说，相比于BSR，MSR更适合探测强噪声背景下的微弱信号。

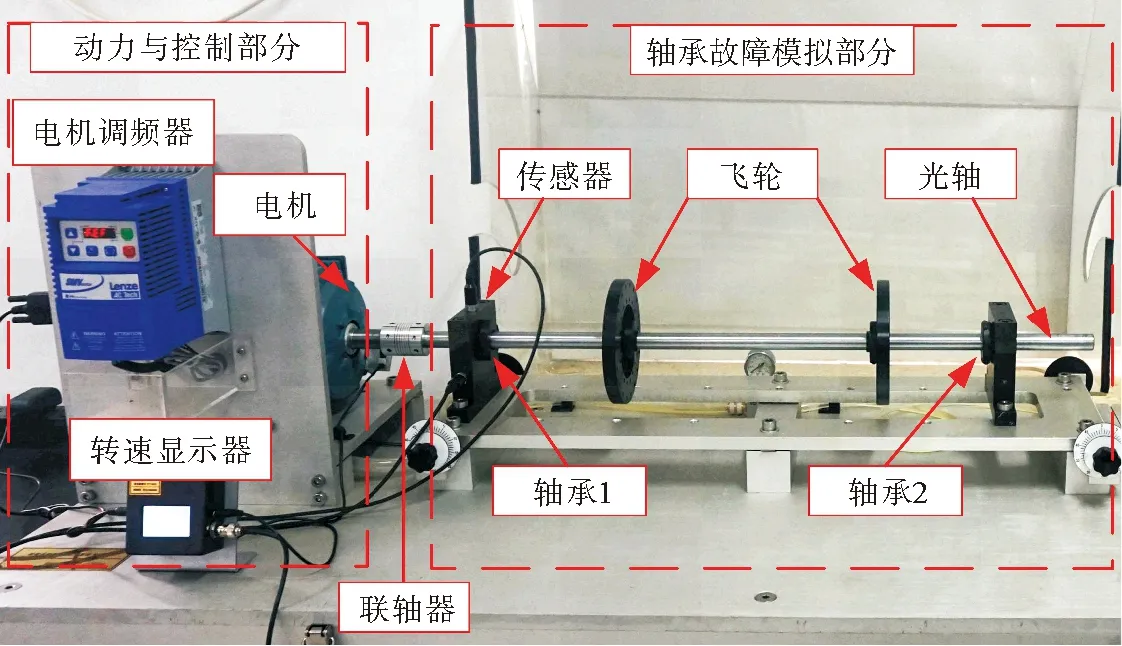
图7 轴承故障模拟试验台Fig.7 Bearing fault test rig

3 轴承故障案例验证

3.1 轴承预植故障试验

轴承预植故障试验台如图7所示。该试验台由三部分组成，即动力与控制部分、轴承故障模拟部分和振动数据采集部分(未在图7中显示)。动力与控制部分由电机(提供动力)、电机调频器(控制电机输出转速)和转速显示器(显示电机实时转速)组成。轴承故障模拟部分由两深沟球轴承套件(型号ER-12K，主要尺寸如表1所示)、飞轮(提供径向负载)和光轴组成。振动数据采集部分由振动加速度传感器、数据采集卡和数据采集软件组成。

分别进行内圈预植故障试验(内圈0.5mm宽深沟槽)和滚动体预植故障试验(单个滚动体0.5mm深沟槽)。预植故障轴承安装于轴承1位置。传感器安装在轴承1附近，采集竖直方向振动加速度数据。每次试验设置参数如下：电机转速fr为20 r/s，采样频率fs为12.8 kHz，总采样时间t为1 s。根据电机转速和轴承主要齿轮，分别计算轴承内圈故障和滚动体故障的特征频率，如表1所示。

表1 ER-12K轴承主要尺寸和故障特征频率Tab.1 Main dimensions and fault characteristic frequencies of Bearing ER-12K

3.2 内圈故障案例

首先分析轴承内圈故障信号。采用20阶Butterworth高通滤波器(截止频率为1kHz)滤除低频信号，采用希尔伯特变换求取包络信号(消除直流分量)。其波形和功率谱如图8a和b所示。经过共振解调后，内圈故障特征频率fic得到增强。由图8b可知，包络信号中包含了较强的旋转频率谐波2fr和3fr。为降低谐波影响，采用谱编辑技术消除谐波2fr和3fr，即将信号中谐波2fr和3fr对应的傅里叶变换幅值置零再进行傅里叶逆变换，所得信号及其功率谱如图8c和d所示。将消除谐波后的信号作为驱动信号和噪声信号的叠加分别输入到BSR系统和MSR系统中，以最大化SR输出SNR为目标，用CS搜索最优参数，分别得到最优BSR输出和最优MSR输出，如图8e～h所示。CS参数设置如表2所示。

表2 BSR和MSR系统下的CS参数设置Tab.2 CS parameter set of BSR and MSR

对比图8d、f和h可知，BSR和MSR的输出SNR均远远大于输入SNR(-9.237 7 dB)，故BSR和MSR都能够提升微弱信号。分析图8f可知，在BSR输出中，高频成分得到显著压缩，而低频成分(低于fic)得到了增强，这验证了BSR的低通滤波的效果。对比图8f和h可知，1)MSR输出SNR大于BSR输出SNR，故MSR性能优于BSR；2)因C=-0.994≈-1，故匹配稳态势函数可近似认为仅包含一个势阱，MSR转换为单稳态随机共振；3)当MSR转化为单稳态随机共振时，MSR输出的高频成分得到压缩，低频成分略微提高，但小于BSR的低频提高程度。

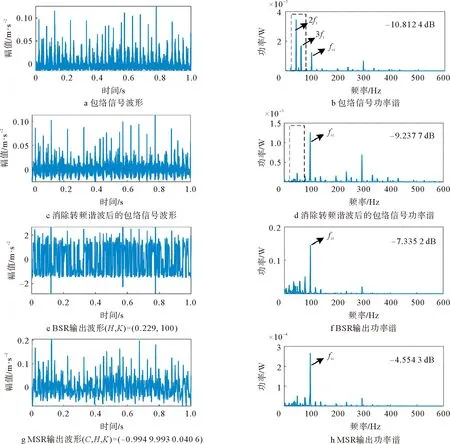
图8 轴承内圈故障信号分析结果Fig.8 Analyzed results of the bearing inner race fault signal

3.3 滚动体故障案例

相比于轴承内圈故障信号，滚动体故障信号就比较微弱了。下面对滚动体故障信号进行分析。采用20阶Butterworth高通滤波器(截止频率为1kHz)滤除低频信号，采用希尔伯特变换求取包络信号(消除直流分量)，其波形和功率谱如图9a和b所示。显然，滚动体故障频率fbc十分微弱，几乎淹没在强大的噪声背景中。将包络信号作为驱动信号和噪声信号的叠加，分别输入到BSR系统和MSR系统中，以最大化SR输出SNR为目标，用CS搜索最优参数，分别得到最优BSR输出和最优MSR输出，如图9c～f所示。CS的参数设置与内圈故障案例相同，如表2所示。

对比图9b、d和f可知，BSR和MSR的输出中的频率fbc成分显著提高，BSR和MSR的输出SNR均远远大于输入SNR(-26.487 1dB)，故BSR和MSR都能够显著提升微弱信号。对比图9d和f可知，1)MSR输出SNR大于BSR输出SNR，故MSR性能优于BSR；2)因C=0.950∈(0, 1]，故匹配稳态势函数包含3个势阱，MSR转换为三稳态随机共振；3)当MSR转化为三稳态随机共振时，MSR输出的高频成分得到压缩，低频成分略微提高。

综合上述两案例，可得出下列结论：1)MSR能够在压缩高频成分的同时，显著提升故障特征频率成分，且效果优于BSR；2)基于MSR的轴承故障诊断方法能够有效提升轴承故障特征频率，便于判断轴承健康状态。