基于领导者对称的多智能体系统可控性研究
2019-09-23纪志坚渠继军
仉 伟,纪志坚,渠继军
(青岛大学自动化学院,山东 青岛 266071)
0 引言


本文的工作主要包括两部分:首先,基于对非平凡等价划分的不可控情形的研究,考虑了自同构结构对系统可控性产生的影响,本文在命题1中给出了系统存在自同构的判定条件,然后讨论了单领导者系统和多领导者系统的可控性。其次,通过理解领导者对称,将具有对称性的单领导者系统利用置换矩阵推广到多领导者对称,与文献[19,23]所做的有所不同,本文研究的不仅仅是具有对称性的单领导者系统,而是更为一般的系统,并在定理2给出了多领导者对称的判定条件,同时指出领导者对称与系统可控性的关系,从而为系统可控性研究提供了新的视角。
1 预备知识
1.1 图论
首先,介绍图论的一些基本内容,在多智能体网络系统中,图中的节点表示智能体,边表示智能体之间的相互连接,具有相同边的节点相互交流。无向图G表示为G=(V,E),由顶点集V(G)和边集E(G)⊆V×V组成。其中V={1,2,…,n},E={(i,j)|i,j∈V(G)},n表示图中节点的个数。没有环结构及多重边结构的图称为简单图,本文研究的都为简单图。顶点i的相邻点集合为N(i)={j∈V(G)|(i,j)∈E(G)}。如果图G中任意两个不同的顶点i,j间都存在一条道路,则称图G是连通的。外部控制输入信号施加在输入节点上,输入节点集合为S={i1,i2,…,iq},并且满足i1 图G的邻接矩阵A(G)∈Rn×n描述一个图的节点之间信息交流,A(G)=(aij)n×n,aij定义为 (1) 其中,wij表示边的权重,论文中没有特殊说明的权重皆设为1,邻接矩阵都为对称矩阵。度矩阵D(G)=(dij)n×n,dij定义为 (2) 图G的对角矩阵D的对角线元素等于图G的邻接矩阵相对应行的所有元素相加之和,也可表示为D(G)=diag(d1,…,dn),dn为与顶点相连接的边的总个数。 拉普拉斯矩阵L(G)∈Rn×n为表示图中顶点之间关系的另一种矩阵,L(G)=(lij)n×n,lij定义为 (3) 下面介绍划分,等价划分和松弛等价划分。 定义2如果对于任意的s,t∈Ci,有 (4) 定义3无向图G的顶点集V(G)的一个划分π的特征矩阵为这样的矩阵Pπ∈Rn×r,当顶点i∈Cj时,pπ(ij)=1,否则pπ(ij)=0。 对含有n个智能体的一阶积分器线性系统,其连续时间动力学模型可以表示为 (5) 其中,xi(t)∈Rn为第i个节点在时间t的状态,ui为第i个节点的外部控制输入i∈{1,2,…,n},式(5)即为系统的一致性协议。在无加权的多智能体网络系统中,控制输入协议描述为 (6) 在控制输入协议(6)下,系统(5)可写成具有n个节点的整合形式 (7) 若用集合Ic={i1,…,im}⊂{1,…,n}表示控制节点集。加入外部输入控制后,系统(7)可转化为以下动态系统 (8) 定义4设ψ为图G=(V,E)上的置换,若存在任意节点i,j∈V和(i,j)∈E,ψ将节点i映射为ψ(i),节点j映射为ψ(j),当且仅当(ψ(i),ψ(j))∈E,则称ψ为图G的自同构映射,简称自同构(AUT)。 其中,节点i,j和(ψ(i),ψ(j))有相同的邻居关系,即置换ψ保持各节点之间的邻接关系不变。若i≠ψ(i),则称i,ψ(i)为自同构节点。G的所有自同构映射构成G的自同构群记为T。 定义5设A(G)是图G的邻接矩阵,ψ为G的顶点集合V(G)上的一个置换,则ψ是图G的一个自同构,当且仅当AP=PA(等效地LP=PL),则称P为ψ的置换矩阵。显然地,P为非单位矩阵。P表示为 (9) 每一组自同构节点i,ψ(i)可以划分到同一个胞腔内,进而诱导图的等价划分。已知自同构可以诱导等价划分,则从上述定义可知,等价划分是松弛等价划分的一种情况,而自同构诱导的划分是等价划分的一种情况,所以我们就可以利用自同构诱导的等价划分来分析系统的可控性。松弛等价划分、等价划分和自同构诱导的划分之间的关系如图1所示。 定义6对于有连接的非平凡胞腔b|Ci|=k|Cj|,其中b是Cj中每个节点的邻居数,k是Ci中每个节点的邻居数。如果b=|Cj|,k=|Ci|,则称非平凡胞腔Ci和Cj的连接为完全连接,否则称为不完全连接。 图1 AEP、EP和AUT之间的关系Fig.1 The relationship among AEP, EP and AUT 系统结构存在自同构,进而诱导等价划分时,得到以下几点。 1)对于非平凡胞腔,若系统为完全连接,其通信路径是相同的;若系统为不完全连接,则通信路径是相似的。 2)如果改变非平凡胞腔内节点的顺序,拉普拉斯矩阵L行和列均不变。 3)设系统的拓扑结构在等价划分后存在非平凡胞腔,系统存在自同构,该系统的拓扑结构一定是具有对称性和循环性的。循环性即按顺序将节点位置依次改变,不考虑标号,边的位置不变。 引理1[22]设G=(V,E)的拉普拉斯矩阵为L,令π={C1,C2,…,Ck}是V的划分,并且令Pπ是π的特征矩阵。若π是G的松弛等价划分,则存在k×k阶矩阵Q,使得 LPπ=PπQ (10) 命题1设图G的拉普拉斯矩阵为L,令P为置换矩阵,当且仅当满足PTLP=L时,存在非平凡胞腔,使得系统的拓扑结构存在自同构。 注1置换矩阵为每一行和每一列都只有一个元素为1,其余的元素为0。当一个矩阵乘上一个置换矩阵时,得到的新矩阵是原来矩阵的行或列经过置换后得到的。置换矩阵也被定义为单位矩阵的某些行或列交换后得到的矩阵。 证明:设图G的拉普拉斯矩阵为L,令π是G的松弛等价划分。以下是对定理1的充分性和必要性的证明。 (充分性)假设可以找出一个非单位矩阵P,使得PTLP=L,此时非单位矩阵P在改变该系统的拉普拉斯矩阵L的行和列后,系统的拉普拉斯矩阵L不变,边的位置不变,连接情况没变。则P一定为置换矩阵,G的顶点集合V(G)上存在置换,该系统的拓扑结构一定存在自同构。 例1图2验证自同构代数等式条件PTLP=L,图2a,2b为自同构。 图2 七节点无向图Fig.2 Seven-node undirected graph 图2b为图2a图的自同构,经计算得出A1=A2,D1=D2,L1=L2。图2a到图2b仅仅是节点2与节点3交换位置,即标号位置发生改变,整体的拓扑结构未发生变化,边的连接情况也没发生变化,则可以找到一个P 使得PTL1P=L2,即L1=L2。则可知图2a所示的系统满足自同构的代数等式条件,该系统的拓扑结构存在自同构,图2b为图2a图自同构的一种情况,节点2与节点3为自同构节点,显然地,节点4与节点6也为自同构节点。从图2上的这两种自同构可以看出节点2与节点3有对称关系,节点4与节点6也有对称关系,由此可以引出以下领导者对称的定义。 定义7若系统中只有一个领导者l1,存在n×n阶置换矩阵P,使得P(-Lf)=(-Lf)P,则称系统关于l1对称,即为单领导者对称系统。 其中,Lf为选取一个节点作为领导者后跟随者系统的拉普拉斯矩阵,P(-Lf)=(-Lf)P,PT(-Lf)P=(-Lf),跟随者系统中存在自同构,即跟随者系统是对称的,系统为单领导者对称系统。 若图G的自同构ψ满足ψ(i)=i,将所有节点i的自同构节点ψ(i)构成的子群记为Ti。保持每个节点不变的置换称为自同构群的单位元。Ti中元素既保持每个节点间的邻接关系不变,又固定节点i不动,记Ti>1表示Ti中含有非单位元,下面将对称性推广到多领导者系统。在图G的自同构群T中,所有跟随者中Ti的集合记为Tf。用Tf>1表示Tf中含有非单位元,对于多领导者对称系统,定义如下。 定义8设系统中有N个领导l1,l2,…,lN,若Tf>1,则称系统关于l1,l2,…,lN对称,即为多领导者对称系统。 定理1当且仅当l1,l2,…,lN的跟随者子图中自同构群Tf>1,系统关于领导者l1,l2,…,lN对称。 证明:设系统中有n个跟随者和N个领导者l1,l2,…,lN,对所有跟随者从1到n进行标记,领导者的标号为n+1,n+2,…,n+N。根据跟随者与领导者的划分,将图G的邻接矩阵和拉普拉斯矩阵写成如下的分块矩阵。 其中,Af为所有跟随者构成的子图Gf的邻接矩阵。δn+1,…,δn+N为n维列向量,领导者与跟随者之间的邻接情况表示为 (充分性)设系统关于领导者l1,l2,…,lN对称,则存在n×n阶的置换矩阵Pf使得Pf(-Lf)=(-Lf)Pf,即PfAf=AfPf。 注2在图G中选择l1,l2,…,lN为领导者,若系统为多领导者对称的系统,此时跟随者系统一定至少存在一个自同构Ti,即系统存在自同构,则可利用跟随者系统中的自同构结构来研究系统可控性。 图3 六节点无向图Fig.3 Six-node undirected graph 例2在图3所示的拓扑结构中,选取不同的领导者来说明单领导者对称与多领导者对称。 在图3所示拓扑结构中,ψ(2)=3,ψ(3)=2,ψ(4)=5,ψ(5)=4,系统存在自同构。选取节点1作为领导者,自同构诱导的划分为πl1={{1},{2,3},{4,5},{6}}。此时存在6×6阶非单位置换矩阵P,使得Pf(-Lf)=(-Lf)Pf,则系统是关于l1对称的系统。同理,分别选取节点2,3,4,5,6作为领导者,系统都是关于所选领导者对称的系统,即为单领导者对称系统,共有6种选取方式。选取节点1,2作为领导者,自同构诱导的划分为πl1,l2={{1,2},{3},{4,5},{6}},此时T3=1,T4=2>1,T5=2,T6=1,系统关于l1,l2对称。选取节点1,2,3作为领导者,自同构诱导的划分为πl1,l2,l3={{1,2,3},{4,5},{6}},此时T4=2>1,T5=2>1,T6=1,系统关于l1,l2,l3对称。选取节点1,2,3,6作为领导者,自同构诱导的划分为πl1,l2,l3,l6={{1,2,3,6},{4,5}},此时T4=2>1,T5=2>1,系统关于l1,l2,l3,l6对称。共有21种选取领导者方式使系统为多领导者系统。若选取节点1,2,4作为领导者,自同构诱导的划分为πl1,l2,l4={{1,2,4},{3},{5},{6}},此时T3=1,T5=1,T6=1,系统不是领导者对称系统。 下面利用等价划分来分析系统存在领导者对称与可控性之间的关系,对于具有领导者-跟随者结构的系统,设系统中共有N个领导者l1,l2,…,lN和n个跟随者,所有跟随者及跟随者之间形成的连接关系图记为Gf,πf为Gf的等价划分。 定义9若N个领导者各自独占一个胞腔Cr+1={l1},Cr+2={l2},…,Cr+N={lN}。令πl1,l2,…,lN=πf∪Cr+1∪Cr+2∪…∪Cr+N,则πl1,l2,…,lN称为图G的多领导者的等价划分。 引理2[20]若系统的拓扑结构图G存在非平凡的松弛等价划分,则系统不可控。 注3由等价划分与松弛等价划分的定义可知,等价划分是松弛等价划分的一种情况,若系统的拓扑结构图G存在非平凡的等价划分πl1,l2,…,lN,则系统不可控。 定理2若自同构诱导的划分为非平凡的等价划分πl1,l2,…,lN,系统为领导者对称系统,跟随者系统存在非平凡胞腔,则系统不可控。 证明:系统的拓扑结构图G存在自同构诱导的非平凡等价划分πl1,l2,…,lN,设划分含有m+N个胞腔,若|Ci|=θi,即胞腔Ci中含有θi个节点,对Ci中的点用θi个连续数字进行标记,考虑N个领导者的情况。 设l1与s个胞腔Co1,Co2,…,Cos相邻接,l2与t个胞腔Cp1,Cp2,…,Cpt相邻接,…,lN与k个胞腔Cq1,Cq2,…,Cqk相邻接,按图G的划分形式对矩阵A和B进行相应分块。 其中,Ai,j为θi×θj阶矩阵, 由邻接矩阵A定义可知,Ai,j的每行元素之和相等。已知跟随者系统存在自同构,那么至少存在两个自同构节点,使可控性判别矩阵C中同一胞腔中的点对应的行向量相等,故rank(C)≤m。又因为πl1,l2,…,lN是非平凡的划分,可知rank(C) 注4系统在选取领导者后系统仍存在自同构,自同构诱导的划分为非平凡的等价划分πf,此时系统不可控,领导者无法将存在自同构的非平凡胞腔里的跟随者区别开来,从而无法将它们实现单独控制,这便导致了系统的不可控性。 图4 自同构诱导顶点集合V(G)的等价划分Fig.4 Automorphism induces the equivalent partion of vertex set V(G) 例3如图4所示,自同构群T=AUT(G)由转置ψ1={1,2},ψ2={5,6,7}生成,则自同构诱导顶点集合的等价划分为π={C1,C2,C3,C4},其胞腔为C1={1,2},C2={3},C3={4},C4={5,6,7}。施加固定的外部控制输入,控制输入矩阵为B=[ei1,…,eim]。此时选取不同的领导者,来分析系统存在自同构诱导的等价划分时,系统不可控的情况。 1)选取一个节点作为领导者时,系统为单领导者系统。选胞腔C1中的节点1作为领导者施加固定的控制输入时,T5=3>1,T6=3>1,T7=3>1,系统为单领导者对称系统,胞腔C4中节点5,6,7,收到的控制输入是完全一致的,胞腔内不能实现对某个节点的单独控制,该系统不可控。同理,节点2,3,4,5,6,7作为领导者,系统也不可控,仅考虑单领导者系统有7种选择是不可控的。 2)选取多个节点作为领导者时,系统为多领导者系统。选取胞腔C1中的节点1,胞腔C4中的节点5作为两个领导者加控制输入,此时T6=2>1,T7=2>1,系统为多领导者对称系统,胞腔C4存在自同构,系统不可控。同理,选取胞腔C1中的节点1,2,胞腔C4中的节点5作为三个领导者加控制输入,此时T6=2>1,T7=2>1,系统也为多领导者对称系统,胞腔C4存在自同构,系统不可控。对于多领导者系统,共有72种选择使系统不可控。 综上所述,例3假设系统的输入固定,那么个体间形成的信息交换图存在自同构时,选取了不同领导者分析可控性,总共有126种领导者选取方式。选取平凡胞腔作为领导者施加控制输入,系统不可控。选取存在自同构的非平凡胞腔作为领导者施加不同的输入时,若跟随者系统中的胞腔仍然有非平凡的,则不论跟随者之间的连接情况如何,系统总是不可控的,共有79种不可控选择。 本文利用图论知识作为工具,研究了自同构诱导的等价划分以及领导者选择对可控性产生的影响。首先,命题1中给出了自同构的判定条件,即给出了基于图论来判断存在自同构的系统可控性的方法。其次,将单领导者对称系统的概念推广到多领导者对称系统,并在定理1中给出了判定条件。最后,利用等价划分研究了一类由于系统存在自同构造成的不可控系统,同时也研究了跟随者系统中存在自同构造成的不可控系统。本文可以看出,多智能体可控性与拓扑结构有着密不可分的关系,多智能体可控性可以看作等价于拓扑结构图的可控性。因此,利用图论工具来研究可控性具有重要的理论和现实意义,作为未来的研究方向,我们要研究多智能体网络可控性的充要条件。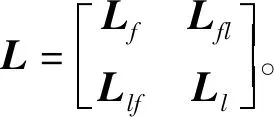


1.2 系统模型

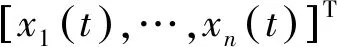
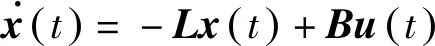

2 自同构及系统可控性分析
2.1 自同构及其判定条件





2.2 可控性分析







3 总结
