钢桥面板U肋嵌补段对接焊缝多轴疲劳特征
2019-09-23
(河海大学土木与交通学院, 江苏南京210098)
0 引言
正交异性钢桥面板是钢桥结构中采用较多的一种桥面板形式[1-3]。服役几十年以来,疲劳开裂一直是困扰其发展的主要问题之一[4-6]。在众多疲劳细节中U肋对接焊缝常采用现场施工,焊接质量难以保证,在荷载重复作用下,易产生疲劳裂纹。U肋在钢桥面板起到纵梁的作用,如果产生疲劳损伤,将会影响整个桥面结构的安全性。
目前针对钢桥面板疲劳易损细节的疲劳评估,国内外学者开展了大量工作。其中多采用名义应力和热点应力与线性累积损伤理论相结合,并基于S-N曲线进行疲劳评估。如国外有学者对顶板与U肋局部截断试件进行了疲劳试验,通过焊趾处的名义应力拟合S-N曲线,对比分析了80 %熔透焊缝与完全熔透焊缝疲劳强度的差别[7];还有学者通过有限元建模和足尺试件的疲劳试验,采用带缺口细节处的热点应力对比分析了不同方法下得到的疲劳寿命[8];国内有学者还通过有限元方法获取热点应力,并基于热点应力给出了正交异性钢桥面板的疲劳验算过程[9]。同样地,针对U肋对接焊缝细节,一些学者采用实桥监测的手段得到了细节处的名义应力,并基于S-N曲线给出了该细节的疲劳寿命[10-11]。目前基于S-N曲线的寿命评估多是采用正应力作为名义应力或热点应力的单轴疲劳评估,而实桥中对接焊缝实际处于多轴疲劳状态。如能分析得出对接焊缝在多轴疲劳下的受力特征和影响多轴疲劳的因素,为该细节多轴疲劳理论的建立提供参考,将是具有重要意义的。
根据实桥U肋对接焊缝构造细节,建立节段整体模型与对接焊缝子模型。通过平板有限元模型的单、多轴疲劳模拟,提出评定多轴疲劳的标准。为了探究对接焊缝细节多轴疲劳开裂原因,结合U肋结构力学模型内力分析与各关注点应力状态对其进行了受力分析;通过对比远近端面主应力对其进行了变形分析。通过对比各关注点的正应力与绝对值最大的主应力的偏差,从结构非对称性和荷载作用位置两个方面探究了对接焊缝处多轴疲劳的影响因素。
1 有限元建模及多轴疲劳评定准则
1.1 有限元模型
以某公路悬索桥正交异性钢桥面板为工程背景,其顶板厚12 mm,横隔板厚8 mm,横隔板间距3 200 mm,U肋截面尺寸为300 mm×280 mm×6 mm,U肋间距为600 mm,钢材采用Q345qD。钢桥面板与U肋采用80 %熔透焊缝连接,横隔板与U肋采用双面角焊缝连接,U肋对接焊缝采用带钢衬垫板的单面坡口焊缝。
为了兼顾计算负担与计算精度的要求,采用子模型建模策略,分别建立钢桥面板节段模型与U肋对接焊缝细节子模型,将节段模型的计算结果以边界条件形式施加于子模型,从而计算U肋对接焊缝焊趾处的应力状态。节段模型纵向包括5道横隔板,横向包括7道U肋[12];采用C3D8R六面体单元划分,全局种子设为20 mm;边界条件设为约束顶板,U肋和铺装的所有平动自由度以及横隔板的所有平动加转动自由度。对接焊缝距离No.3号横隔板500 mm;子模型横向取600 mm,纵向取200 mm,竖向取342 mm;采用C3D8R六面体单元和C3D10四面体单元进行网格混合划分,非焊缝区域采用20 mm六面体网格划分,对重点关注的焊缝区域采用1 mm六面体网格细化,细化区域与其他区域采用四面体网格过渡。有限元模型钢材弹模取2.06×105MPa,铺装弹模为1 000 MPa,泊松比均取0.3[13]。节段模型与子模型如图1所示。
荷载取用《公路钢结构桥梁设计规范》规定的疲劳计算模型Ⅲ中的一个单侧双轮荷载[14],加载面积为600 mm×200 mm,荷载集度为0.5 MPa。采用Fortran语言编制的ABAQUS用户子程序DLOAD实现移动加载,考虑对接焊缝细节所处的位置,以No.2号横隔板中心为原点O,横向分为11个加载工况,横向加载间距为150 mm。纵桥向,车轮从No.2号横隔板移动至No.4号横隔板,加载间距取200 mm,共计33个荷载步。加载工况如图2所示。
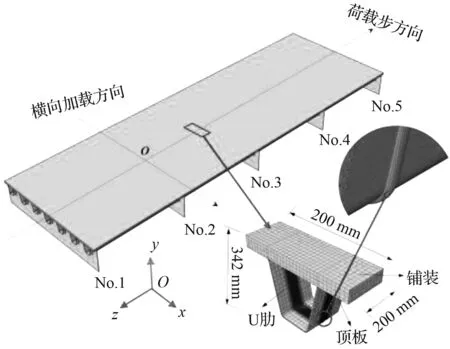
图1 有限元模型
Fig.1 Finite element model
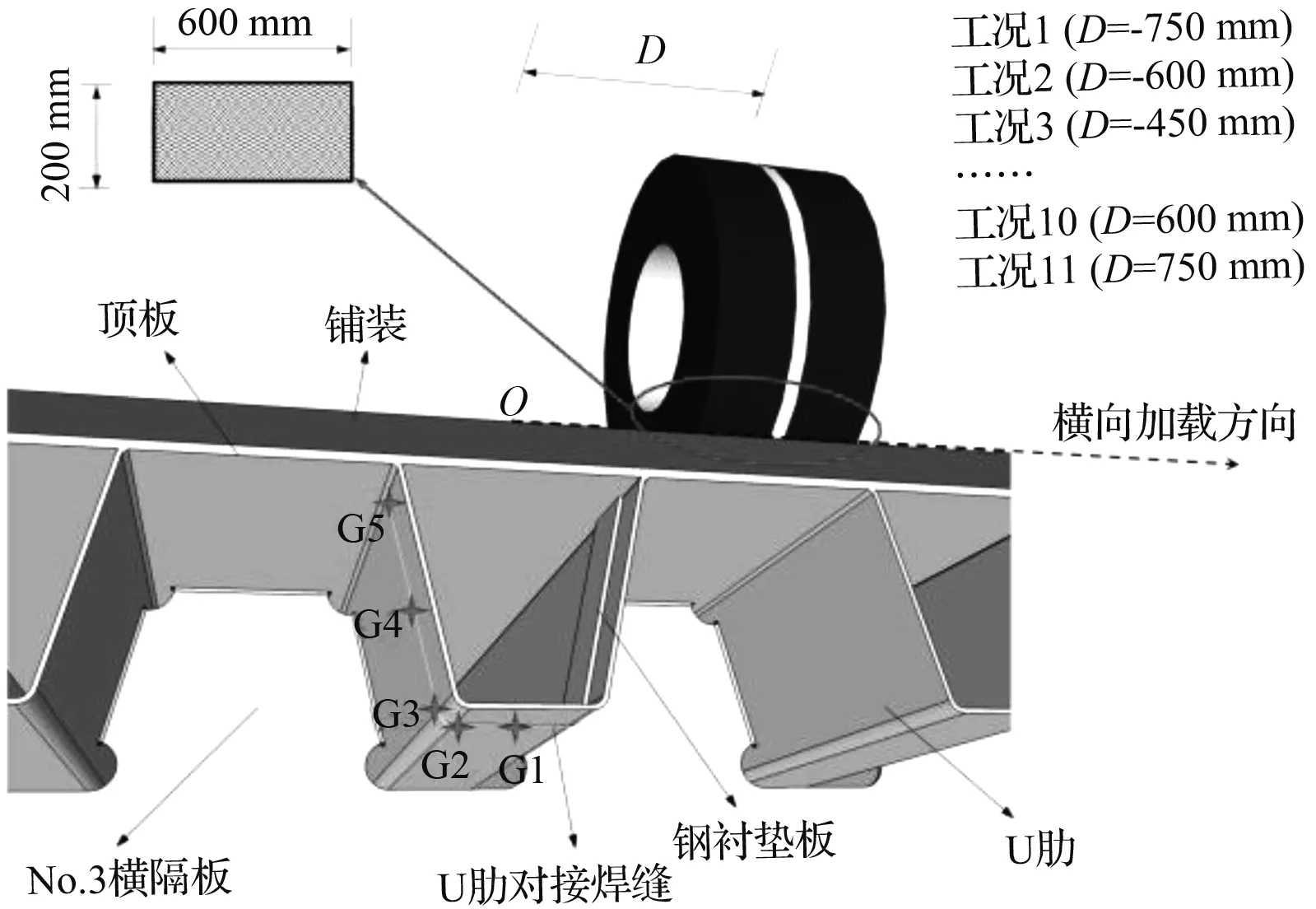
图2 加载工况及关注点示意
Fig.2 Loading cases and concern points
实桥运营中,纵肋主要承受弯矩和剪力的作用。纵肋在弯矩作用下,将在U肋底板G1点产生较大的弯曲正应力,该处对接焊缝在高应力反复作用下,易产生循环滑移和微裂纹的扩展;G2和G3是U肋底板与腹板的过渡点,几何形状的变化可能加重该处的应力集中,使得高应力区进一步扩大;荷载作用下,U肋腹板中点G4主要承受循环剪应力作用,是较易产生循环滑移和微裂纹的位置;对于对接焊缝与顶板—U肋焊缝衔接点G5,局部几何形状的突变将引起应力集中,循环荷载易造成该处的疲劳损伤。综合考虑后选取上述易开裂点作为关注点来研究对接焊缝的多轴疲劳特征,如图2所示。
1.2 多轴疲劳评定准则
为了准确便捷地判断U肋对接焊缝细节是否处于多轴疲劳状态,有必要提出一种合理简单的多轴疲劳评定准则。在对疲劳易损细节进行研究时,分别以横桥向、纵桥向和面板高度方向建立坐标系,如图1所示。定义沿坐标系轴向的应力分量中幅值较大的正应力为主要应力分量,对于对接焊缝细节,主要应力分量为σz。一般情况下,裂纹的扩展方向与主应力方向垂直[15]。仅当主应力等于主要应力分量时,扩展方向才与主要应力分量方向垂直。而多轴疲劳效应是引起主应力与主要应力分量不相等的主要因素之一。因此考虑对比主要应力分量与主应力的量值来判断细节是否处于多轴疲劳状态。在主应力类别中,绝对值最大的主应力较能反映实桥对接焊缝处于交变应力循环作用的情况,所以这里的主应力考虑采用绝对值最大的主应力。
建立平板有限元模型,通过改变边界条件和施加周期载荷以模拟其分别处于各类单、多轴疲劳的情况。平板尺寸为200 mm×200 mm×10 mm,网格尺寸为5 mm,材料属性等和1.1中节段模型保持一致。以拉压单轴、拉压多轴、弯曲单轴和弯扭多轴为例[16],提取平板中心点处主要应力分量σn与绝对值最大的主应力σm进行对比,如图3所示。
图3(a)中绘制了拉压单轴和拉压多轴的主要应力分量σn与绝对值最大的主应力σm的时程曲线。从图中可以看出拉压单轴的σn曲线变化趋势与应力集度q随时间的变化趋势是一致的,变化过程中的应力峰值接近1MPa,这近似符合弹性力学平面应力状态的情况。图3(a)中拉压单轴的σn曲线与σm曲线完全重合,而拉压多轴中的σn曲线与σm曲线在几个区间内存在显著差异。拉压多轴的σn与σm差值占σm比例的最大值达到172.6 %。图3(b)为弯曲单轴和弯扭多轴的σn与σm时程曲线。同样,弯曲单轴的σn曲线与σm曲线相互重合,而弯曲多轴的σn与σm存在明显差异,两者差值占比σm的最大值为37.6 %。
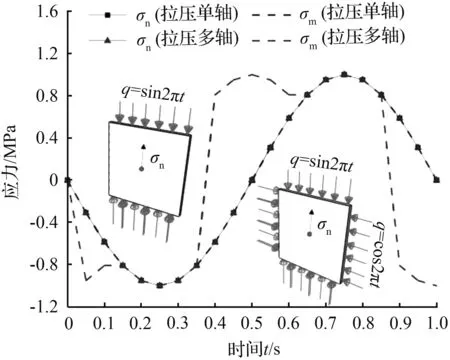
(a) 拉压单轴与拉压多轴
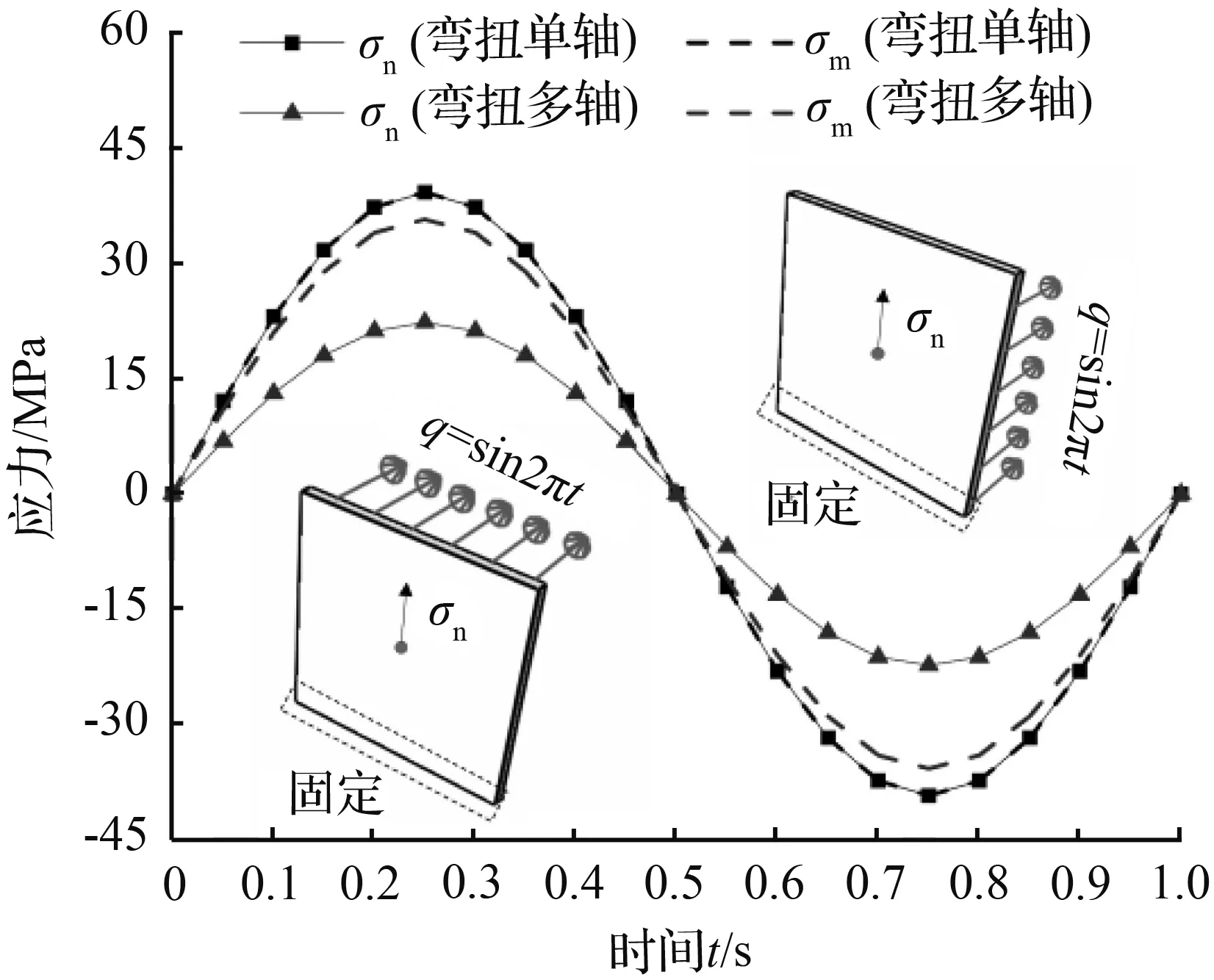
(b) 弯曲单轴与弯扭多轴
图3 单轴疲劳与多轴疲劳应力对比图
Fig.3 Stress comparison between uniaxial fatigue and multiaxial fatigue
综合各类单、多轴疲劳的结果,单轴疲劳状态下的σn与σm的时程曲线相互重合,而多轴疲劳状态下的σn与σm在量值上存在显著差别,两时程曲线不再重合。针对对接焊缝细节,可通过对比焊趾处纵桥向正应力与绝对值最大的主应力的时程曲线来判断其是否处于多轴疲劳状态。
2 多轴疲劳裂纹成因分析
2.1 受力分析
为了探究多轴疲劳状态下对接焊缝的开裂原因,可从细节处的主导应力及主导变形进行分析。
对接焊缝处纵肋的内力形式是影响局部应力分布的重要因素之一。横隔板在厚度方向很薄,相应的抗弯惯性矩较小,因此对纵肋的纵桥向变形约束很小。在对实桥简化进行内力分析时,可将纵肋等效为简支于横隔板上的连续梁体系[17]。

图4 内力影响线Fig.4 Internal force influence lines
图4给出了简化后纵肋在移动荷载作用下的内力影响线。当车轮作用于对接焊缝正上方时,细节承受弯矩和剪力的共同作用。车轮自No.2号向No.4号横隔板移动过程中,弯矩由负值渐变为正值,当车轮跨越No.3号横隔板时,弯矩回归为负值。剪力在车轮跨越对接焊缝细节和No.3号横隔板时均发生变号。车轮作用在细节左侧的剪力远大于作用于右侧的结果,这是由于当车轮作用于接近于横隔板一侧时,No.3号横隔板对U肋的支撑作用显著,减小了荷载平衡对截面剪力的需求。因此,车轮荷载作用下,U肋对接焊缝将主要承受弯矩和剪力的循环作用。
上述内力分析是以结构力学基本假定为前提的,为了夯实补充以上论断,提取车轮荷载作用于细节正上方时(工况6)各关注点的应力分量影响线,如图5所示。图5(a)中G1点的应力峰值接近20 MPa,与由文献[11]实桥监测应变推算得到的应力峰值一致,因此有限元模拟结果是准确可靠的。
从图5中可以看出,除G1点外,各关注点的正应力σz与绝对值最大的主应力σm的时程曲线不完全重合,结合1.2提出的多轴疲劳评定标准来看,这近一步论证了对接焊缝细节实际是处于多轴疲劳状态的。G1~G4点σz曲线变化趋势一致,σz最初为压应力,当车轮荷载接近对接焊缝时,σz变为拉应力,当车轮跨越No.3号横隔板后,σz再次变为压应力。G5点的σz曲线变化趋势与其他关注点的情况正好相反,这主要是由于G5点和其他关注点分别位于U肋截面中性轴两侧造成的。由此可见σz曲线变化趋势与弯矩影响线分析结果是一致的。τyz近似在车轮作用于对接焊缝正上方时取得最大值,这与剪力影响线在对接焊缝处最大的结果相符。G4点τyz的量值远大于其他关注点,说明越靠近截面中性轴,τyz的量值越大,符合截面剪应力呈鱼腹式分布的规律。与内力分析不同的是,G4、G5点σy量值相对较大,这是由于U肋具有一定高度,当荷载作用于对接焊缝正上方时,U肋腹板顶部承受局部压应力作用,引起σy的量值较大。
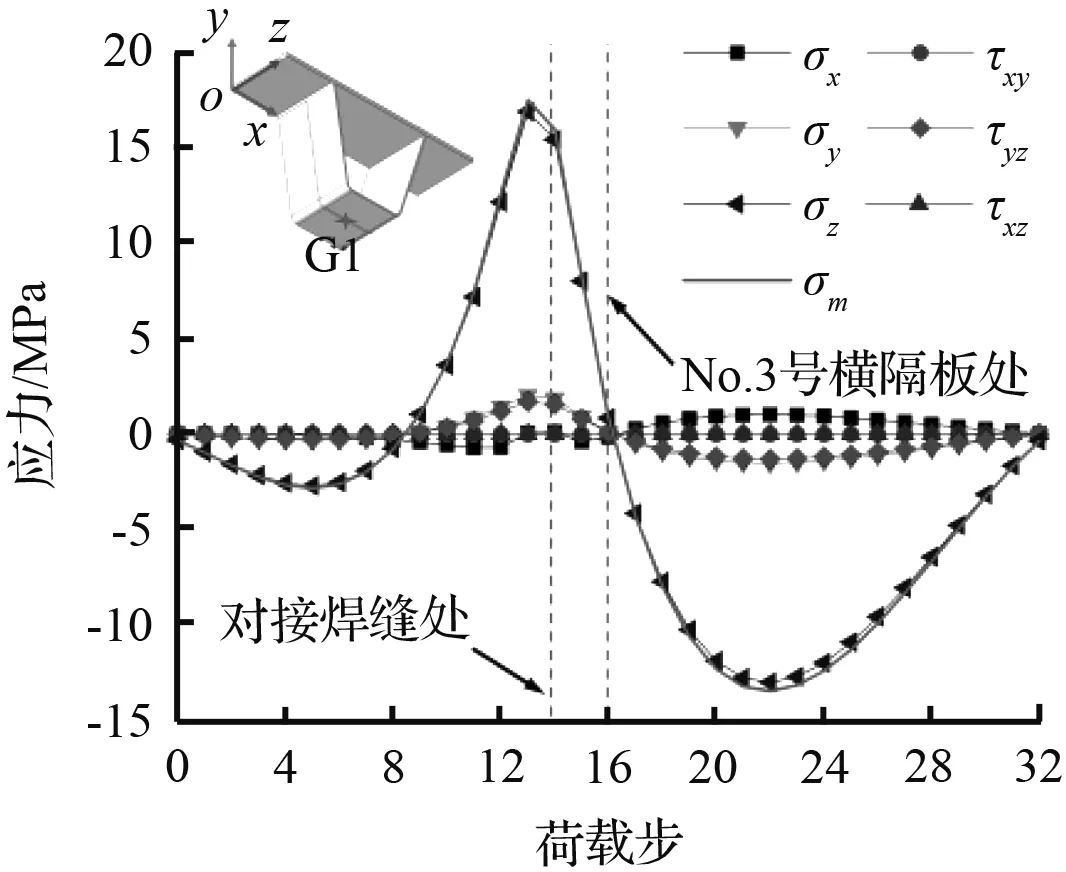
(a) G1点应力影响线

(b) G2点应力影响线

(c) G3点应力影响线
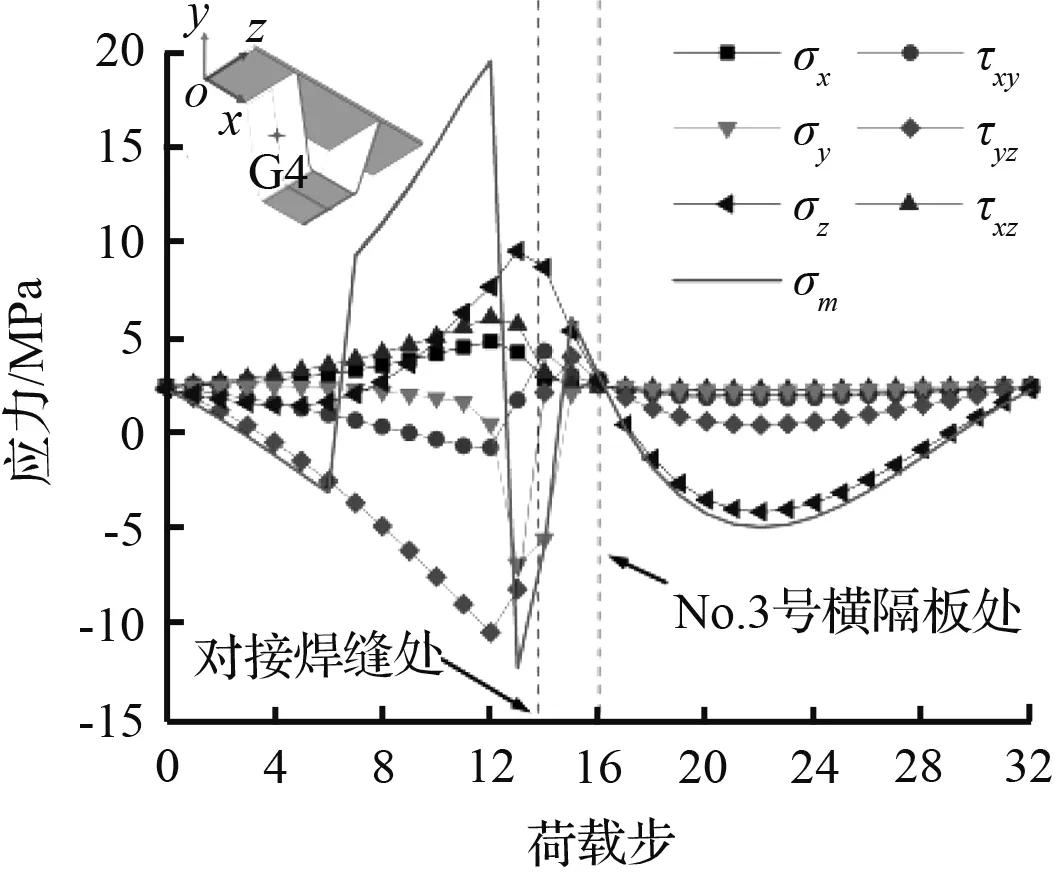
(d) G4点应力影响线

(e) G5点应力影响线
由上述分析可知,对接焊缝处于多轴疲劳状态。对接焊缝处的内力随车轮荷载的纵桥向移动,将发生正负交替变化。由于纵肋主要承受纵桥向弯矩作用,各关注点正应力σz变化最为明显,应力水平远大于其他应力分量。σz对疲劳开裂的贡献最大,实际裂纹扩展方向与σz接近垂直,其他应力分量的存在是引起扩展方向与σz不完全垂直的重要原因。G4和G5点剪应力τyz的水平接近于σz。从开裂机理看,剪应力是疲劳开裂的主要原因[15],τyz对裂纹扩展的驱动作用亦不可忽略。由于车轮的局部作用使得G5点压应力σy的水平也较高。σy以压应力为主,对z方向的裂纹张开具有促进作用。因此,纵桥向正应力σz、截面弯曲剪应力τyz和顶板厚度方向正应力σy的循环作用是引起U肋对接焊缝多轴疲劳开裂的重要原因。
2.2 变形分析
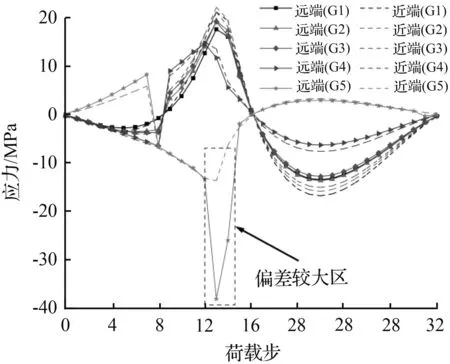
图6 远近端面σm对比 Fig.6 Comparison between σm located in two end faces
为了探究对接焊缝处的主导变形,将U肋厚度方向的内外表面分别定义为远端表面和近端表面。分别提取横向最不利工况下各关注点远近端表面的绝对值最大的主应力σm的影响线,如图6所示。
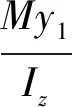
3 多轴疲劳影响因素分析
3.1 结构非对称性因素
由1.1有限元建模可知,节段模型为对称结构,工况6可视作对称结构承受对称荷载作用的情况。从U肋截面看,除G1点位于截面几何对称轴上,其余关注点均位于几何对称轴外。为了探究U肋结构的非对称性对多轴疲劳的影响,提取工况6各关注点纵桥向正应力σz和绝对值最大的主应力σm的时程曲线进行对比,如图7所示。
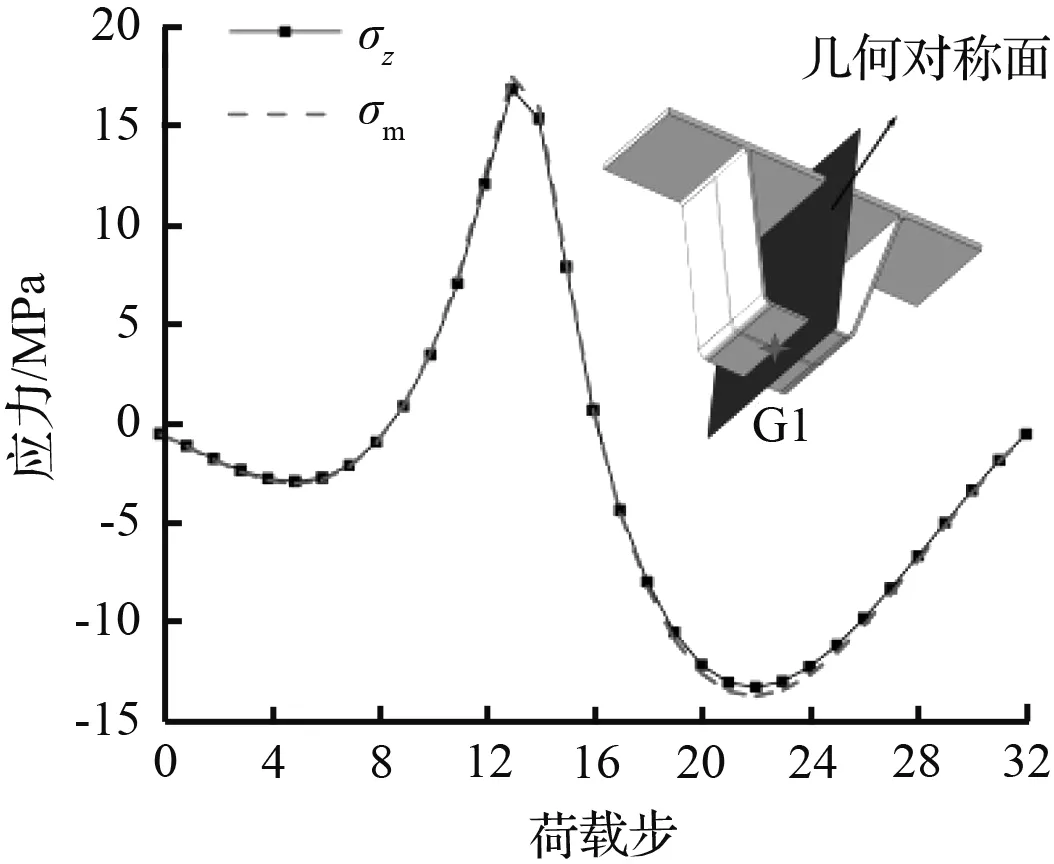
(a) G1点应力对比图

(b) G2点应力对比图
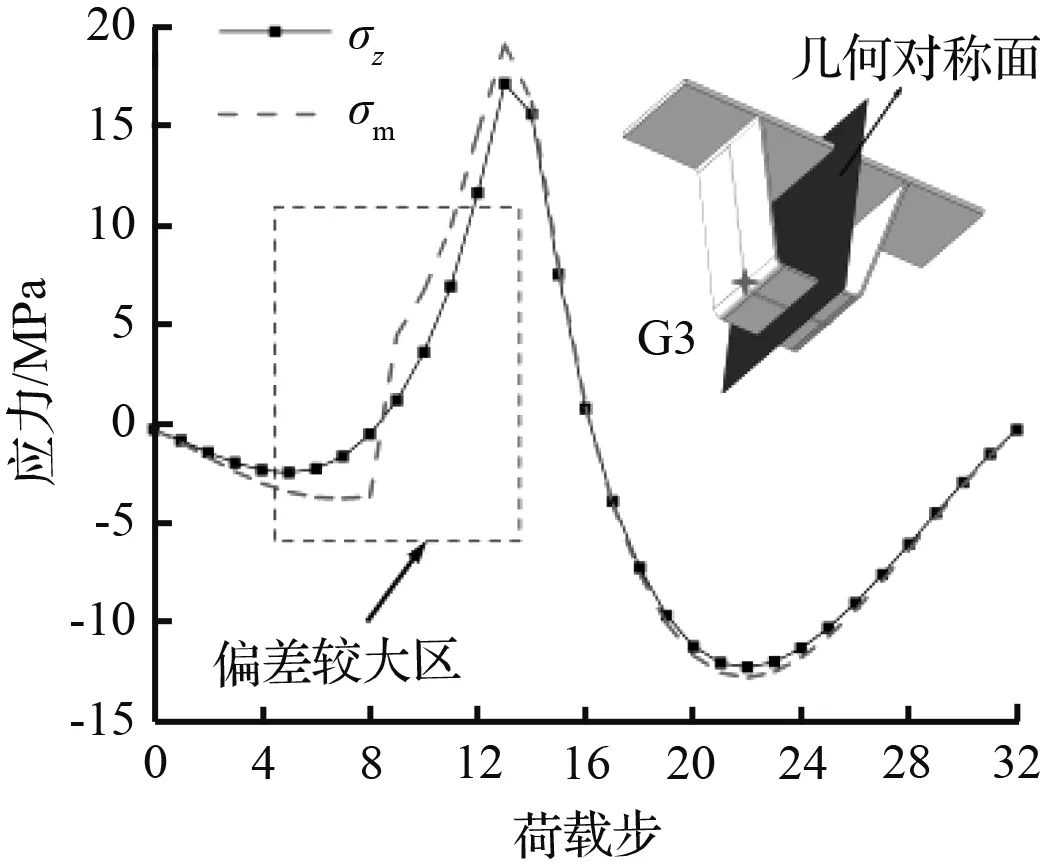
(c) G3点应力对比图
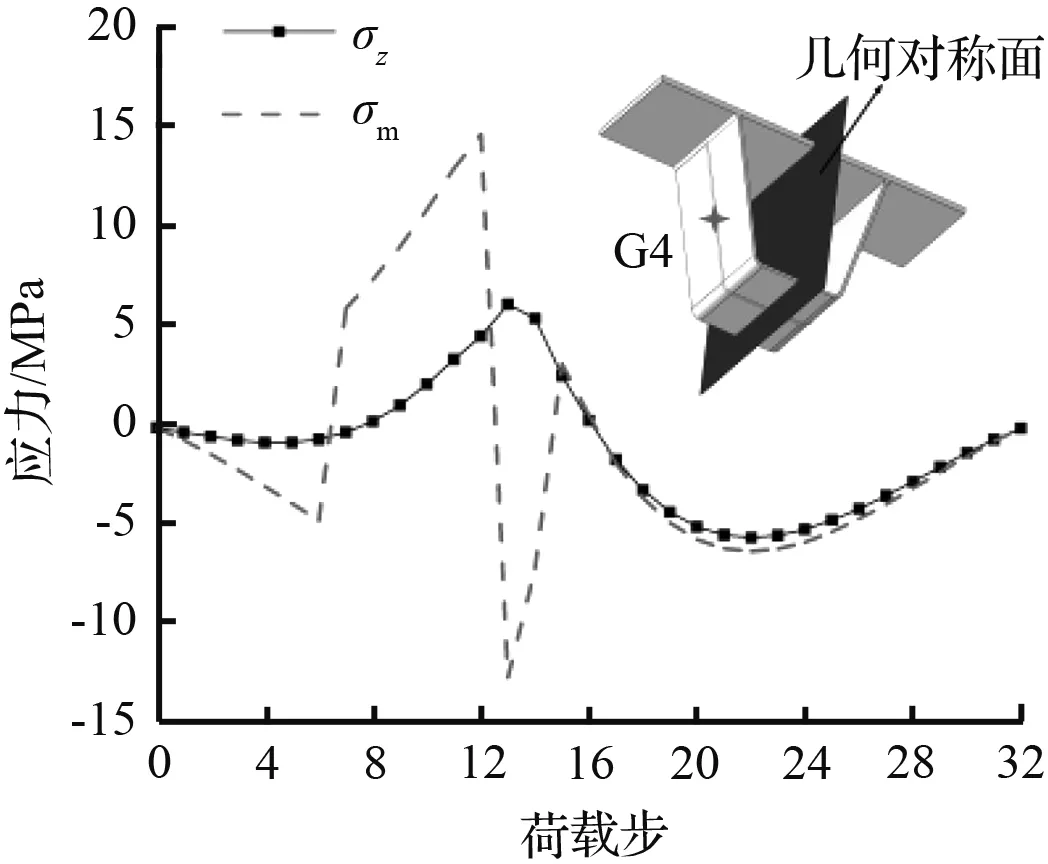
(d) G4点应力对比图
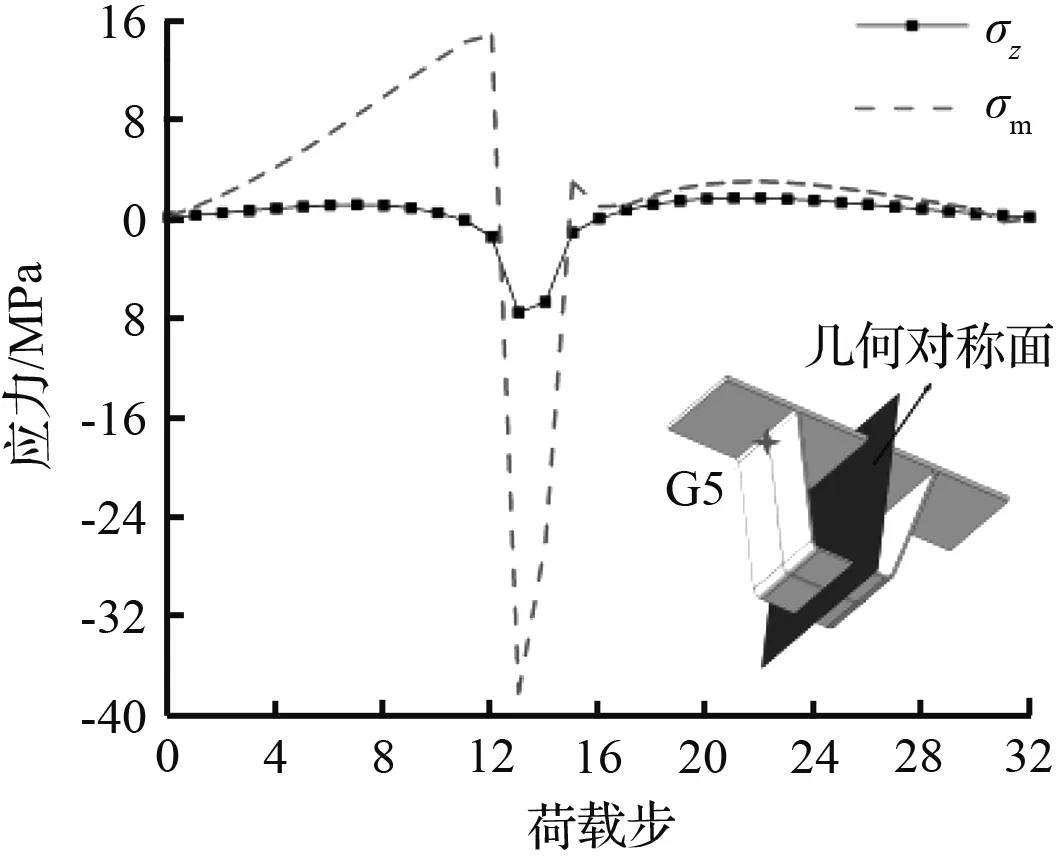
(e) G5点应力对比图
从图7中可以看出,G1点σz与σm曲线相互重合,此时G1点处于单轴疲劳状态。G2和G3点σz曲线与σm曲线变化趋势几乎一致,但在荷载步8附近,两者存在明显的偏差。G2和G3点σz与σm的差值占σm比例的最大值分别为72.8 %和84.5 %,此时多轴疲劳效应较为显著。在荷载步0到16的区间内,G4和G5点的σz与σm曲线变化趋势存在明显差异,σz与σm的差值占σm比例的最大值分别为174.0 %和146.0 %,σz与σm已存在明显偏差,此时关注点处多轴疲劳效应显著。由上述分析可知,由于U肋结构非对称性的缘故,G2~G5点σm与σz曲线存在明显偏差,此时采用多轴疲劳理论对上述关注点进行疲劳评估更为合理。因此,结构非对称性是影响多轴疲劳的重要因素之一。
3.2 荷载作用位置因素
不同的车轮位置将引起细节处应力分布的差异。为了探究车轮位置对多轴疲劳的影响,提取工况6-11下G1点纵桥向正应力σz与绝对值最大的主应力σm进行对比,如图8所示。

(a) 工况6应力对比图
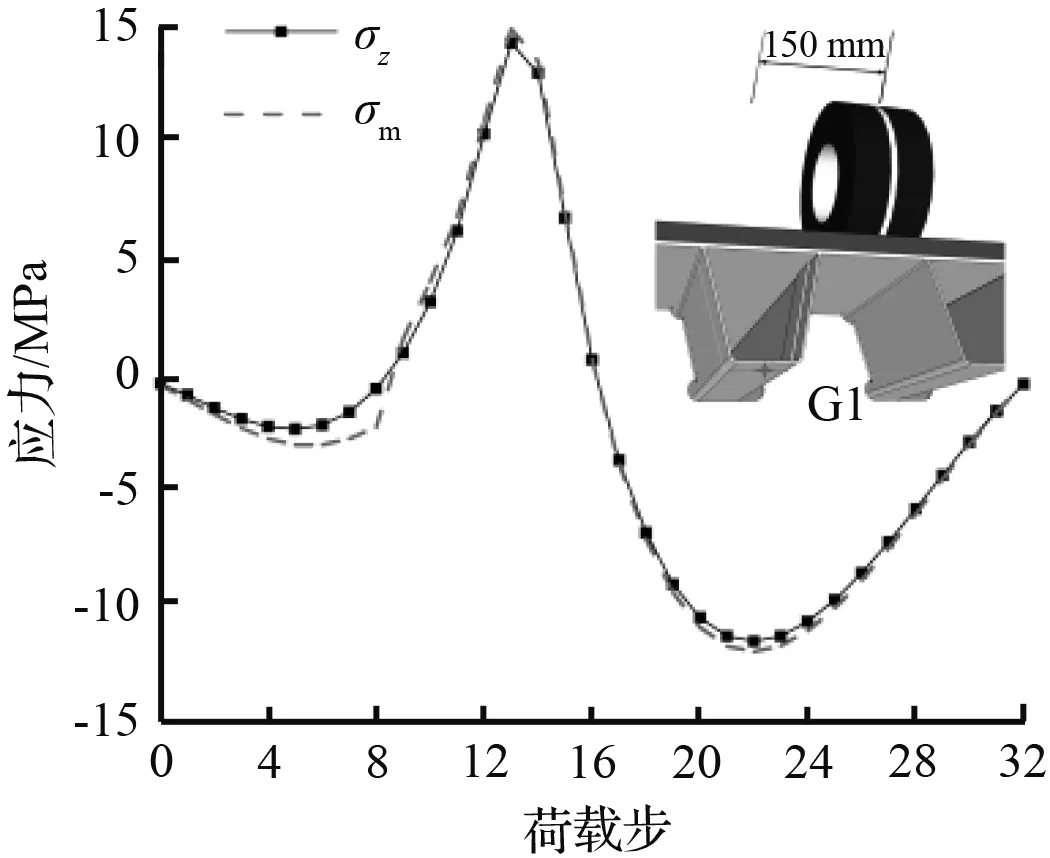
(b) 工况7应力对比图
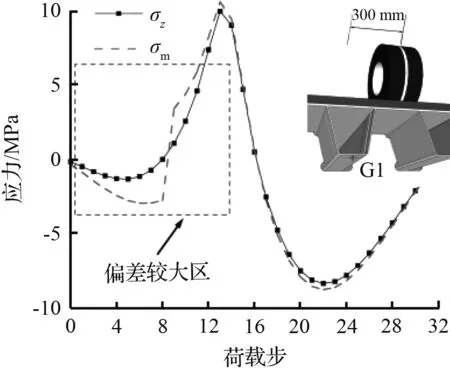
(c) 工况8应力对比图
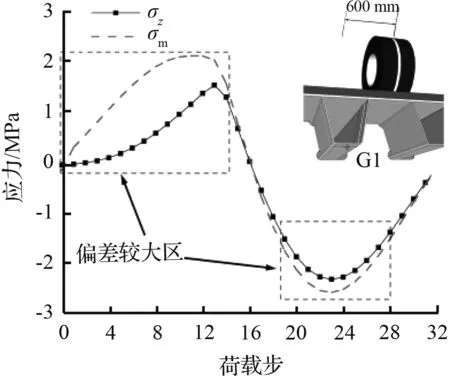
(e) 工况10应力对比图
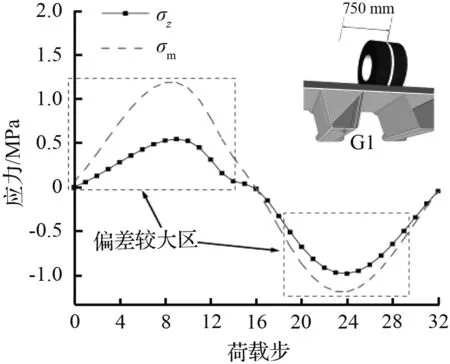
(f) 工况11应力对比图
图8中工况由6变为11模拟了车轮位置逐渐偏离G1点的过程。不同荷载工况下,曲线主要可分为上升段和下降段,σz与σm变化趋势基本一致。随着车轮位置横向偏离G1点越远,图中所示σz与σm的差值越大。当车轮荷载横向偏离G1点大约150 mm以内时,σz曲线与σm曲线近乎重合,σz与σm的差值占σm比例维持在5.0 %以下,只有工况7中的极少数点达到40.0 %,此时G1点多轴疲劳效应并不显著,可近似认为处于单轴疲劳状态。当荷载偏离G1大于300 mm后,σz曲线与σm曲线发生较大偏离,σz与σm的差值占σm比例最大达到103.6 %,此时多轴疲劳效应显著,应采用多轴疲劳理论对关注点进行疲劳评估。经上述分析可以得出,当车轮荷载偏离对接焊缝约300 mm时,考虑采用多轴疲劳理论进行疲劳评估更为合理,荷载作用位置是影响多轴疲劳的另一重要因素。
4 结论
①纵桥向正应力、U肋截面弯曲剪应力和顶板厚度方向正应力的量值较大,三者的循环作用是引起U肋对接焊缝多轴疲劳开裂的重要原因。
②外荷载作用下,U肋空腹薄壁的结构形式导致截面弯曲应力占膜应力的比例很小,对接焊缝处的多轴疲劳开裂主要是由U肋面内变形引起的。
③结构非对称性和荷载偏心作用是影响U肋对接焊缝多轴疲劳的重要因素。多轴疲劳效应随荷载中心线偏离U肋对称轴越发显著。单轴疲劳仅为荷载中心线与U肋对称轴重合时,在U肋对称中心点产生的瞬时效应。
