圆钢管K型弯管节点轴向刚度曲线参数化分析

2019-09-23

广西大学学报（自然科学版） 2019年4期

(贵州大学空间结构研究中心，贵州贵阳550003)

0 引言

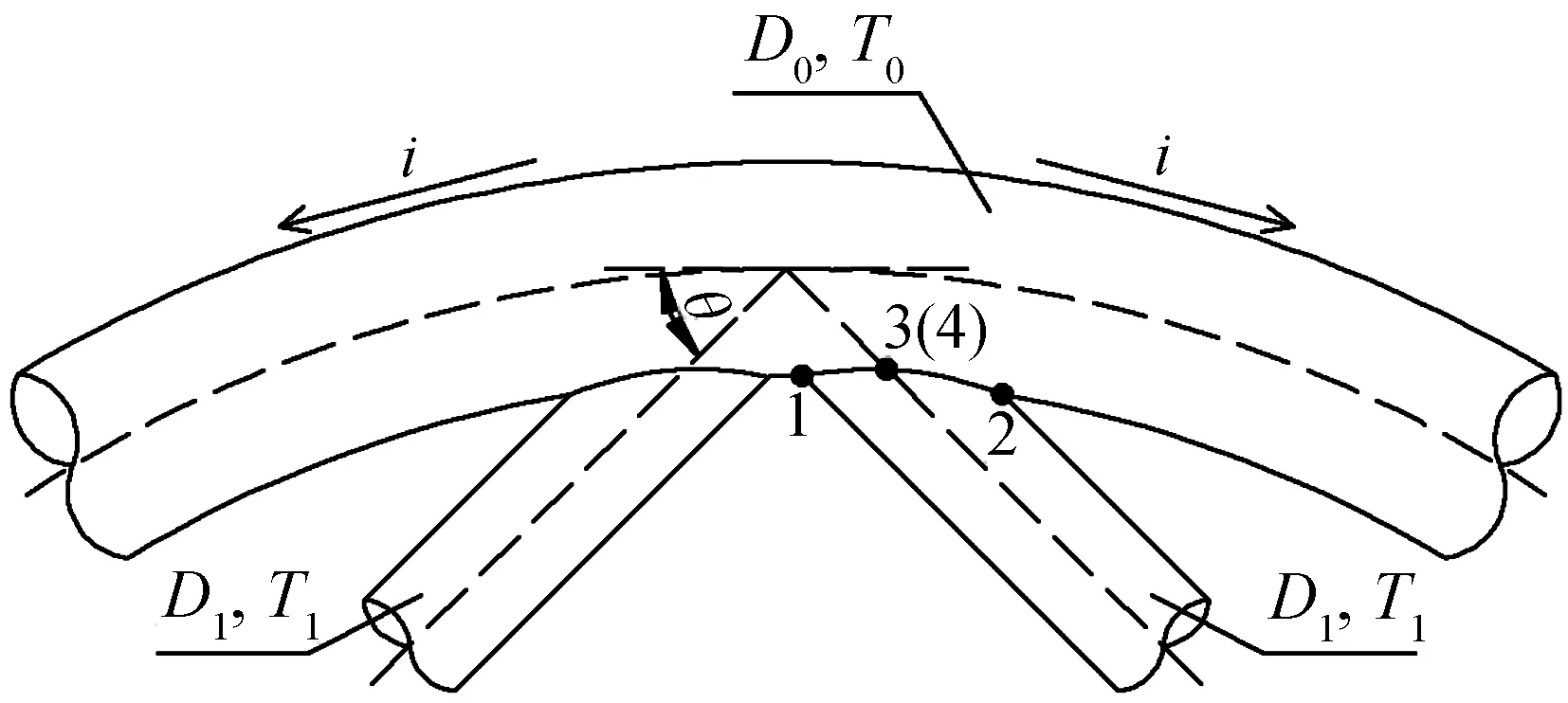
图1 K型弯管节点示意图Fig.1 Schematic of curve steel tube K-joint

钢管截面回转半径大，抗扭刚度好，极限承载力高，广泛应用于体育馆、展览馆等大跨度及超大跨度空间结构。随着计算机多维数控切割技术的成熟，加工相贯线变得非常简单，相贯节点被普遍使用[1]。相贯节点是钢管桁架结构主要的节点形式，具有构造简捷、受力合理、施工方便等优点[2-4]。文献[5-10]研究了钢管K型直管节点的承载力、刚度及冲击荷载作用下的受力性能，其弦杆为平直的。在大跨度、超大跨度屋盖结构中，鱼腹式钢管桁架结构也是一种重要的结构形式；根据结构的受力特点，其结构高度从跨中向支座处逐渐减小，杆件内力较均匀。鱼腹式钢管桁架结构的弦杆均为弯管；弯曲的上弦便于屋面排水，其结构刚度及整体性较好，这种结构找坡方式避免了小立柱找坡带来的不利抗震性能[11]。鱼腹式钢管桁架结构的节点为K型弯管节点，如图1所示。由于弦杆为弯管，在受弦杆轴力时，节点会承受弯矩作用；在受腹杆轴力时，弦杆具有拱的受力特点。这些造成了K型弯管节点与K型直管节点具有不同的刚度特点，需要对其深入研究。

文献[12-13]研究了节点轴向刚度对钢管桁架结构静动力性能的影响，发现节点轴向刚度对结构的变形、自振频率等有较大影响。可见，为了较准确把握钢管桁架结构的力学性能，需要研究相贯节点的轴向刚度。王伟等[8]研究了圆钢管K型直管节点的轴向刚度，其提出的刚度计算公式中，没有考虑弦杆、腹杆轴力的影响。武振宇、梁战场[9]假设腹杆轴力—轴向位移曲线为双折线，研究了各几何参数对矩形钢管K型直管节点初始和屈服轴向刚度的影响。胡涛[14]研究了圆钢管ZYY型节点的初始轴向刚度，并给出了其计算公式。邱国志[15]研究了圆钢管X型节点的轴向刚度—轴向荷载曲线，给出了该曲线的计算公式；发现轴向刚度随着荷载的增加，其逐渐减小。可知，轴向刚度—轴向荷载曲线能较真实地反映节点轴向刚度的变化过程，能为结构的模拟提供较准确的节点轴向刚度计算模型。圆钢管K型弯管节点(本文以下简称圆钢管K型弯管节点为K型弯管节点)主要适用于大跨度、超大跨度结构，需要给出其轴向刚度—轴向荷载曲线，以便进行较准确的结构分析。

本文应用有限元软件ANSYS对K型弯管节点进行了参数化的数值分析，得到了节点轴向刚度的主要影响参数。引入两个无量纲参数，节点轴向刚度因子η和节点轴力因子ω，并确定了这两个因子的关系曲线。通过多元线性回归拟合了节点轴向刚度的计算曲线，为结构分析提供较准确的节点刚度计算模型。

1 节点有限元模型的建立

1.1 相关参数

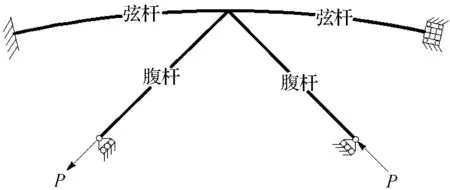
图2 K型弯管节点边界条件及加载方式(不考虑弦杆轴力)Fig.2 Boundary conditions and loading methods of the curve steel tube K-joint

采用有限元分析方法参数化研究K型弯管节点的轴向刚度曲线。如图1所示，节点的组成为弦杆、腹杆(2根腹杆为同种规格圆钢管)，相贯线上1、2两点为冠点，3、4两点为鞍点。弦杆的外径与壁厚分别为：D0、T0，腹杆的外径与壁厚分别为D1、T1；腹杆与弦杆的轴线夹角为θ，弯管坡度为i。本文K型弯管节点的几何参数设置如下：τ0=D0/T0(弦杆外径与其壁厚之比)，τ1=D1/T1(腹杆外径与其壁厚之比)，其中τ0≤100、τ1≤60；β1=D1/D0(腹杆与弦杆外径之比)，且0.2≤β1≤1.0；θ≥30°，i≥0.05[3,16-17]。

1.2 基本假定

节点的计算模型采取以下假定：①腹杆承受的拉力、压力大小相等；②忽略弦杆弯曲制作时产生的附加应力；③节点焊接产生的残余应力忽略不计；④材料本构模型采用双线性强化模型，服从von-Mises屈服准则和随动强化法则，切线模量ET取为0.01E。

1.3 边界条件及加载方式

弦杆、腹杆从它们交汇点伸出的长度分别为其外径的3倍、4倍，以消除加载条件对节点区域受力性能的影响。图2、3分别为不考虑和考虑弦杆轴力的K型弯管节点的边界条件、加载方式，P为沿着腹杆轴线作用的拉力或压力，F为沿着弦杆轴线作用的拉力或压力；图3采用两步加载的方式，以考虑弦杆轴力对节点域刚度的非线性影响。考虑实际的工程要求和节点的受力状态，结合有限元软件的功能，在图2、3中，弦杆的一端考虑为固定支座，其另一端仅允许有沿着弦杆轴线的位移，腹杆端部仅约束其径向位移和环向位移。

(a) 第一步加载

(b) 第二步加载

图3 K型弯管节点边界条件及加载方式(考虑弦杆轴力)
Fig.3 Boundary conditions and loading methods of the curve steel tube K-joint upon the chord bearing axial load

1.4 单元选取及单元划分

有限元分析采用ANSYS弹塑性SHELL181单元，圆钢管的材料采用Q345钢材，泊松比υ取为0.3，弹性模量E=2.06×105MPa。根据圣维南原理，分别采用如下的单元网格划分：弦杆和腹杆的相贯区域采用较密的自由网格划分，该相贯区域外的弦杆和腹杆采用尺寸较粗的映射网格，如图4所示。

图4 K型弯管节点有限元模型Fig.4 Finite element model of the curve steel tube K-joint

2 节点轴向刚度的参数化分析

2.1 节点轴向刚度定义

影响节点刚度的主要参数为：τ0、β1、τ1、θ、i、σz/fy(σz为弦杆横截面承受的平均正应力，fy为钢材的屈服应力)。考虑上述参数的变化，研究节点的轴向刚度。

K型弯管节点的腹杆在受拉或受压时，腹杆产生轴向变形；腹杆与弦杆连接区域的节点域会产生局部变形。节点轴向刚度的基本计算公式如下：

Ki-1=ΔPi-1/Δδi-1,

(1)

式中：Ki-1为第i-1荷载步的节点轴向刚度;ΔPi-1为第i-1荷载步腹杆承受的轴拉力或轴压力增量，ΔPi-1=Pi-Pi-1(Pi、Pi-1分别为第i、i-1荷载步的轴力)；Δδi-1为第i-1荷载步腹杆与弦杆相贯线上沿腹杆轴向的局部位移增量，其为：

Δδi-1=(Δδ1+Δδ2+Δδ3+Δδ4)/4,

(2)

式中：Δδ1、Δδ2、Δδ3、Δδ4分别为相贯线上1、2、3、4点第i-1荷载步沿腹杆轴向的局部位移增量，其为第i、i-1荷载步的局部位移之差。

2.2 节点轴向刚度的无量纲化

为方便计算分析，将节点承受的轴向荷载与其轴向刚度进行无量纲化处理，以获得无量纲的轴向刚度—轴向荷载曲线。节点轴力因子的定义如下：

ωi-1=Pi-1/Nc(腹杆受压)，

(3)

ωi-1=Pi-1/Nt(腹杆受拉)，

(4)

式中：Pi-1为第i-1荷载步腹杆承受的轴压力或轴拉力；Nc、Nt分别为腹杆承受压力和拉力时相应腹杆的承载力设计值，该承载力设计值按文献[16]的圆钢管K型相贯节点的公式进行计算。

节点轴向刚度因子的定义如下：

ηi-1=Ki-1/(EA/L100)，

(5)

式中：Ki-1为第i-1荷载步的节点轴向刚度；E为腹杆弹性模量；A为腹杆截面面积；L100为腹杆的长细比为100时的计算长度；EA/L100为腹杆的参考轴向刚度(本文以下简称腹杆的参考轴向刚度为腹杆的轴向刚度)；腹杆的长细比通常在50～150范围内，取长细比为100的腹杆的轴向刚度(EA/L100)为参考值。

节点轴向刚度因子η是节点抵抗局部变形的刚度与腹杆轴向刚度的比值。当η值很大时，节点抵抗局部变形的能力较强，节点轴向刚度与腹杆轴向刚度串联后的总刚度与腹杆的轴向刚度相差不大，这时节点的轴向刚度可忽略不计；当η值靠近1时，即节点抵抗局部变形的能力与腹杆抵抗轴向变形的能力接近，串联后的总刚度约为腹杆轴向刚度的一半，此时节点的轴向刚度不容忽视；当η值很小时，节点抵抗局部变形的能力较弱，串联后的总刚度比腹杆的轴向刚度小得多，节点轴向刚度对结构的受力影响显著。

2.3 节点的破坏应力云图

K型弯管节点的破坏形态如图5所示。由图5可知，K型弯管节点的破坏主要集中于弦杆与腹杆的相贯区域，此区域的受力较大，且连接部位易产生应力集中。当考虑弦杆轴力时，K型弯管节点的破坏更严重，相贯区域破坏的区域更大，且塑性发展更充分。

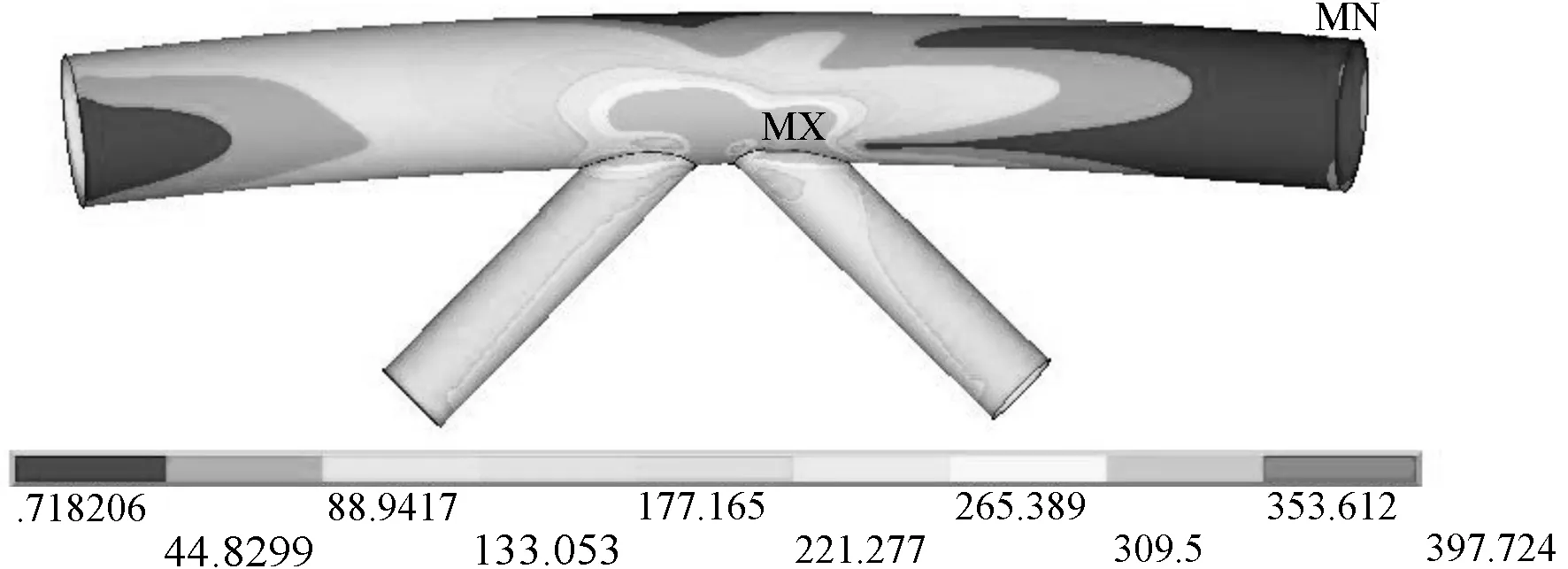
(a) 节点破坏的应力云图(不考虑弦杆轴力)

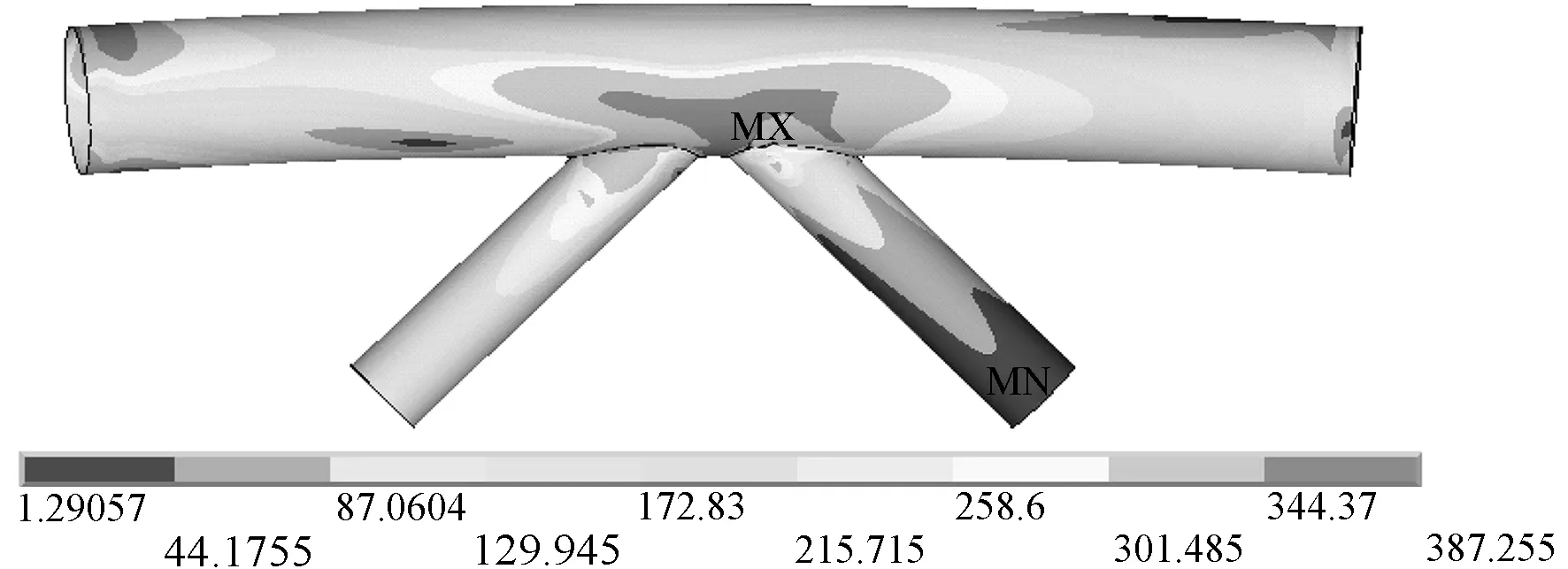
(b) 节点破坏的应力云图(考虑弦杆轴力)

图5 K型弯管节点破坏应力云图
Fig.5 Destructive stress cloud of the curve steel tube K-joint

2.4 τ0对节点轴向刚度的影响

节点在满足构造要求的基础上，腹杆、弦杆的截面几何尺寸如表1所示，其他参数设置为：σz/fy=0、i=0.05、θ=45o。建立了5个有限元模型，以分析弦杆外径与其壁厚之比τ0对节点轴向刚度的影响。

由图6可知，τ0对节点轴向刚度的影响显著，且腹杆受拉时的刚度要优于腹杆受压时。随着弦杆壁厚的增加，腹杆受压时的刚度因子η增加，腹杆受拉时的刚度因子η减小。腹杆受压时的刚度因子η皆小于1，其对结构的受力影响较大；在ω较大时，腹杆受拉时的刚度对结构的受力影响显著。

表1 不同τ0的节点模型参数

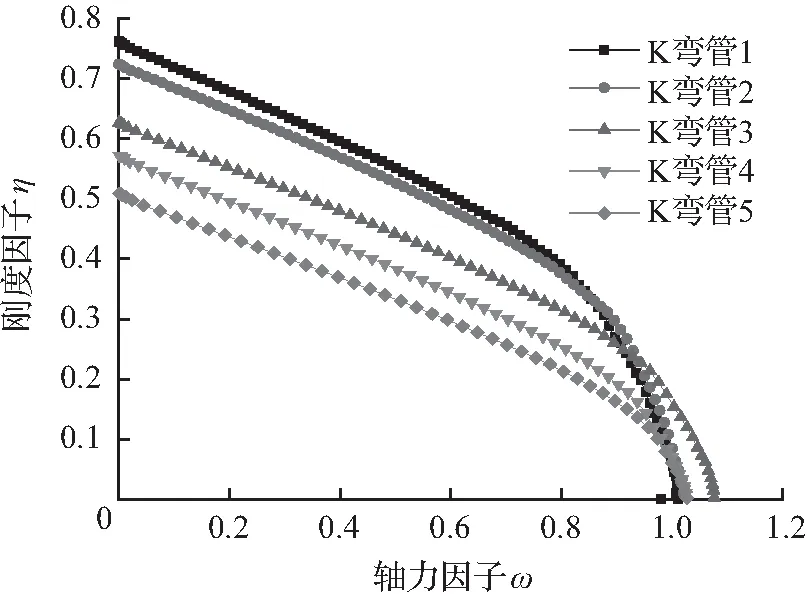
(a) 腹杆受压(τ0变化)

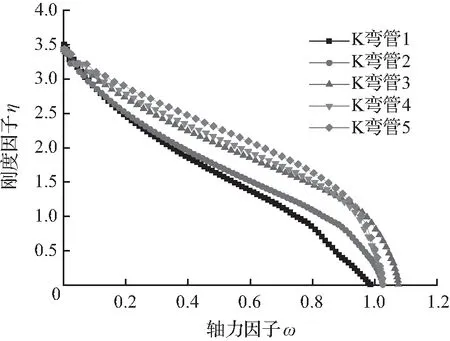
(b) 腹杆受拉(τ0变化)

图6τ0变化的η-ω关系曲线
Fig.6 Relation curve ofη-ωwith different value ofτ0

2.5 β1对节点轴向刚度的影响

节点在满足构造要求的基础上，腹杆、弦杆的截面几何尺寸如表2所示，其他参数设置为：σz/fy=0、i=0.05、θ=45o。建立了5个有限元模型，以分析腹杆与弦杆外径之比β1对节点轴向刚度的影响。

表2 不同β1的节点模型参数Tab.2 Joint model parameters of different β1

由图7可知，随着β1的变化，节点轴向刚度亦变化较大，该轴向刚度对结构的影响也较大。腹杆受拉时的刚度要优于腹杆受压时的刚度，腹杆受压的相贯区域会因刚度不足而率先破坏。

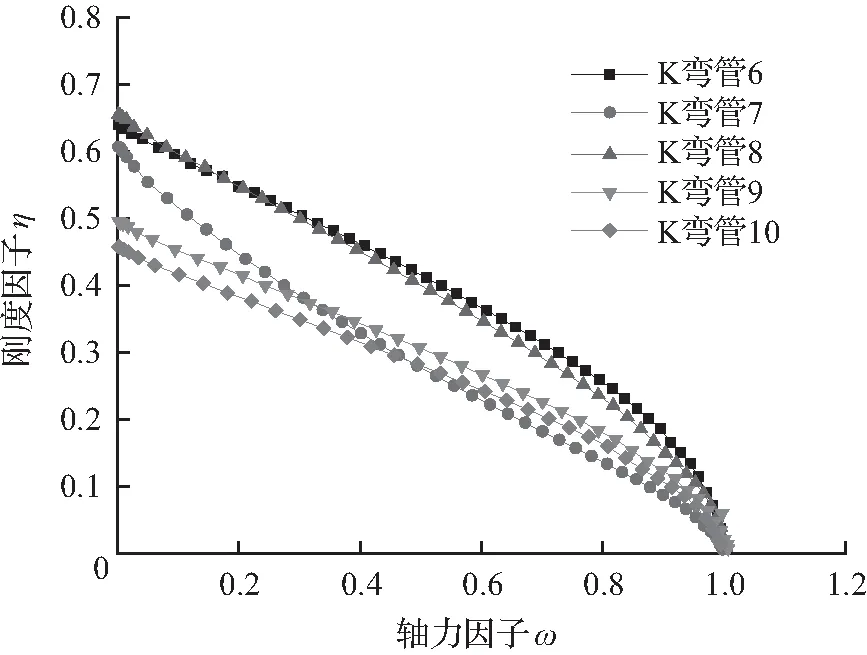
(a) 腹杆受压(β1变化)

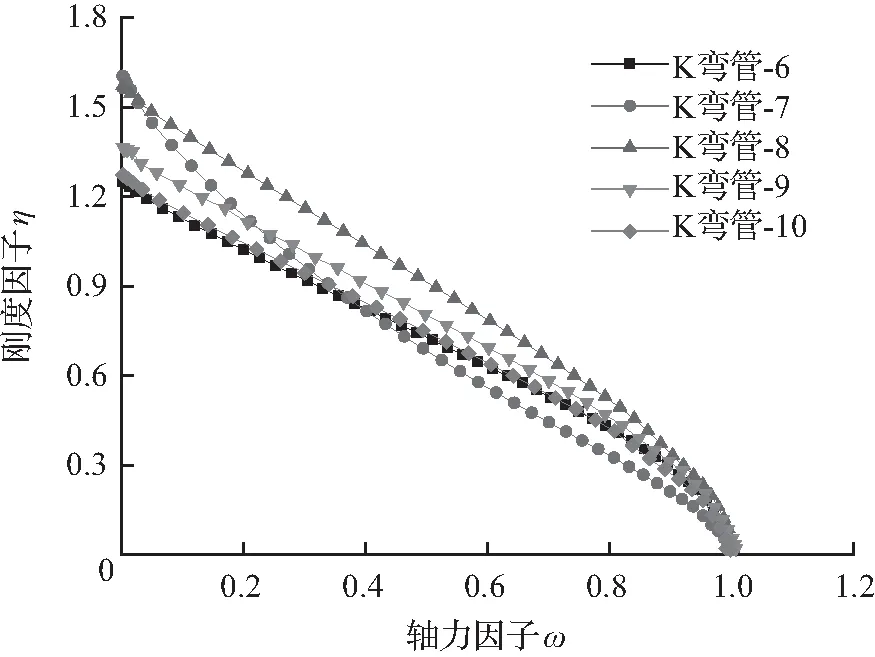
(b) 腹杆受拉(β1变化)

图7β1变化的η-ω关系曲线
Fig.7 Relation curve ofη-ωwith different value ofβ1

2.6 τ1对节点轴向刚度的影响

节点在满足构造要求的基础上，腹杆、弦杆的截面几何尺寸如表3所示，其他参数设置为：σz/fy=0、i=0.05、θ=45o。建立了5个有限元模型，以分析腹杆外径与其壁厚之比τ1对节点轴向刚度的影响。

表3 不同τ1的节点模型参数Tab.3 Joint model parameters of different τ1

由图8可知，随着τ1的变化，节点轴向刚度亦变化较大，该轴向刚度对结构的影响也较大。腹杆受拉时的刚度优于腹杆受压时的刚度。随着τ1的降低，节点轴向刚度皆呈下降趋势，可见应优先选用壁厚较薄的腹杆。

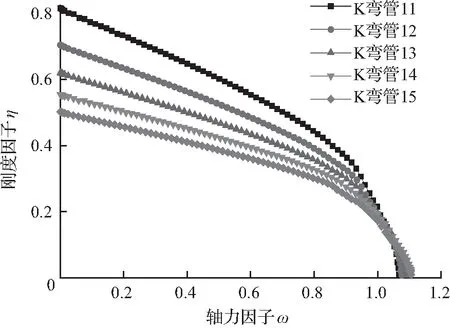
(a) 腹杆受压(τ1变化)

(b) 腹杆受拉(τ1变化)

图8τ1变化的η-ω关系曲线
Fig.8 Relation curve ofη-ωwith different value ofτ1

2.7 θ对节点轴向刚度的影响

节点在满足构造要求的基础上，腹杆、弦杆的相关几何尺寸如表4所示，其他参数设置为：σz/fy=0、i=0.05。建立了5个有限元模型，以分析腹杆与弦杆轴线夹角θ对节点轴向刚度的影响。

表4 不同θ的节点模型参数Tab.4 Joint model parameters of different θ

由图9可知，随着θ的增大，腹杆受压时的刚度逐渐增大，腹杆受拉时的刚度减小；θ变化对节点轴向刚度影响较大，该轴向刚度对结构的影响亦较大。腹杆受拉时的刚度优于腹杆受压时的刚度。

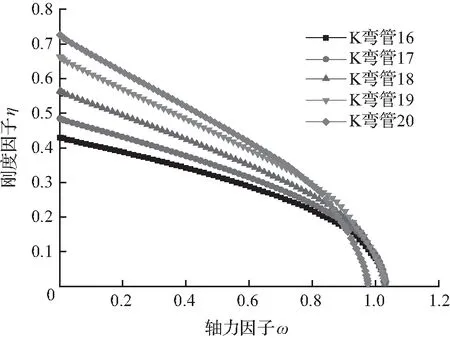
(a) 腹杆受压(θ变化)

(b) 腹杆受拉(θ变化)

图9θ变化的η-ω关系曲线
Fig.9 Relation curve ofη-ωwith different value ofθ

2.8 i对节点轴向刚度的影响

节点在满足构造要求的基础上，腹杆、弦杆的相关几何尺寸如表5所示，其他参数设置为：σz/fy=0、θ=45o。建立了5个有限元模型，以分析弯管坡度i对节点轴向刚度的影响。

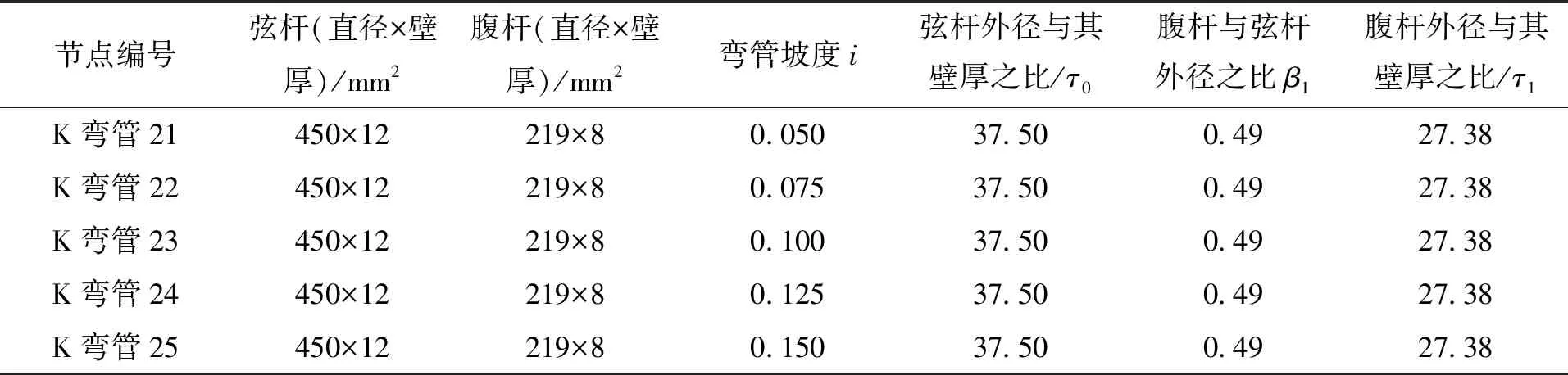
表5 不同i的节点模型参数Tab.5 Joint model parameters of different i

由图10可知，随着i的增大，节点轴向刚度亦有所增大；总的来看，弯管坡度i的变化对节点轴向刚度的影响较小，而该轴向刚度对结构的影响较大。腹杆受压时的刚度优于腹杆受拉时的刚度。

(a) 腹杆受压(i变化)

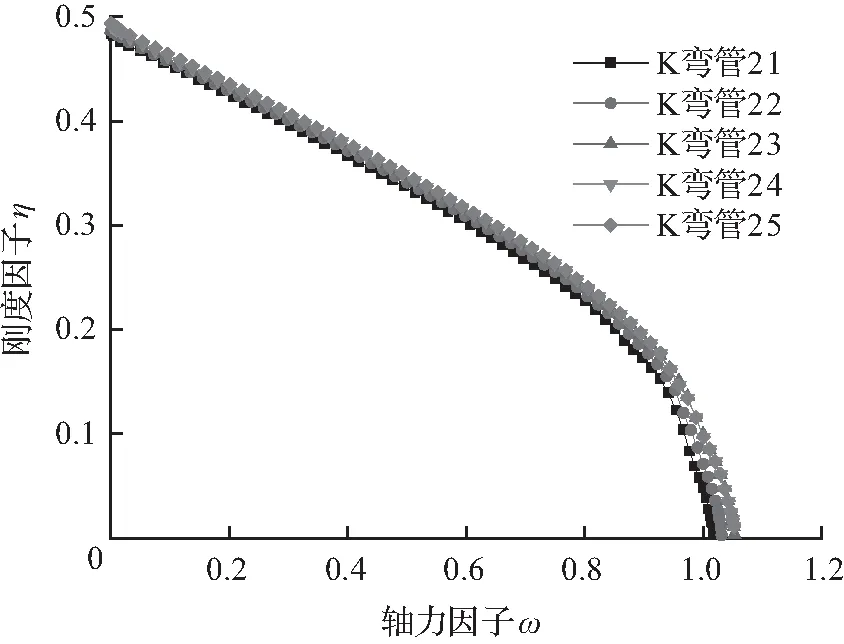
(b) 腹杆受拉(i变化)

图10i变化的η-ω关系曲线
Fig.10 Relation curve ofη-ωwith different value ofi

2.9 σz/fy对节点轴向刚度的影响

节点在满足构造要求的基础上，相关参数如表6所示，弦杆承受轴拉力时σz/fy为正，弦杆承受轴压力时σz/fy为负；其他参数设置为：i=0.05、θ=45°。将节点模型分为弦杆受轴拉力、轴压力两种情况，每种情况建立9个有限元模型，以分析σz/fy对节点轴向刚度的影响。

表6 不同σz/fy的节点模型参数Tab.6 Joint model parameters of different σz/fy

由图11可知，在弦杆承受轴拉力时，腹杆受拉时的刚度优于腹杆受压时的刚度，且两者η-ω关系曲线变化趋势十分相近。在弦杆轴力较小时，节点轴向刚度受其影响较小；随着弦杆轴力的增加，节点轴向刚度的衰减越快，节点的脆性增大。工程应用时，应优先选用截面尺寸大的弦杆，以降低弦杆的轴拉力。

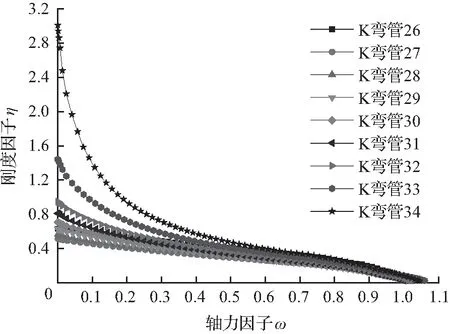
(a) 腹杆受压(σz/fy为正)

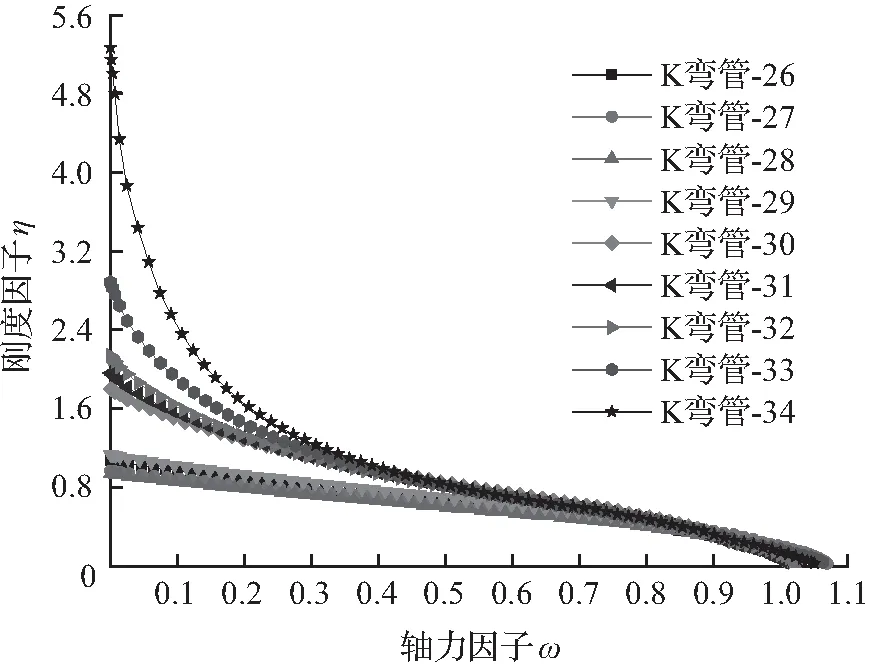
(b) 腹杆受拉(σz/fy为正)

图11σz/fy为正的η-ω关系曲线
Fig.11 Relation curve ofη-ωwithσz/fygreater than zero

由图12可知，在弦杆承受轴压力时，腹杆受拉时的刚度优于腹杆受压时的刚度；在ω较小时，η-ω关系曲线近似为直线。ω<0.79时，节点的轴向刚度随着轴压力的增加逐渐降低；ω>0.79时，节点的轴向刚度随着轴压力的增加逐渐增大。η都小于1，节点的轴向刚度影响是不容忽视的，其对结构的受力是不利的。

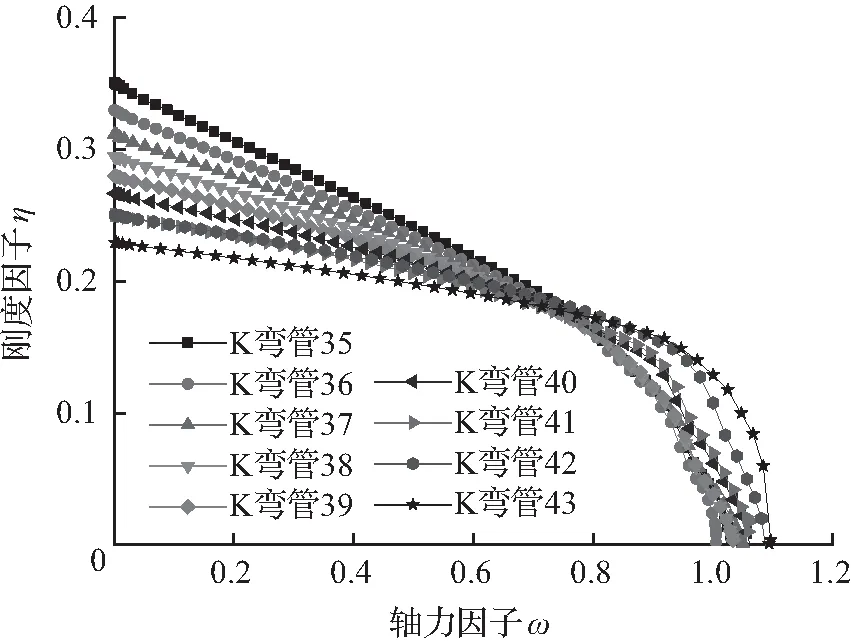
(a) 腹杆受压(σz/fy为负)

(b) 腹杆受拉(σz/fy为负)

图12σz/fy为负的η-ω关系曲线
Fig.12 Relation curve ofη-ωwithσz/fylesser than zero

3 节点轴向刚度曲线的回归计算公式

3.1 节点轴向刚度—轴向荷载的简化曲线

通过前述分析，可见相贯节点的几何参数和杆件的受力条件都会影响节点的轴向刚度，它们对刚度的影响规律各不相同，同时影响的程度也各不相同。节点的轴向刚度随着腹杆受力大小的改变而时刻发生变化，同时在不同参数及条件下η-ω关系曲线的变化趋势也是复杂多变的，并非单一的线性函数关系。本文采用多元线性回归的方法来拟合K型弯管节点的轴向刚度计算公式，即拟合η-ω关系曲线。

图13 η-ω的简化曲线Fig.13 Simplified curve of η-ω

根据前述的η-ω关系曲线的变化趋势，假设该曲线的简化曲线为图13，腹杆受压与腹杆受拉时均采用此简化曲线。在图13中，选取四个点并通过它们将曲线分为两个部分：AB段为直线，BCD段为二次函数曲线。这四点的坐标定义为：A点的坐标(0，η0)，η0为节点的初始轴向刚度；B点的坐标(ω1，αη0)，α为B点对应的η值与初始刚度η0的比值；C点的坐标(ω2，0.5αη0)；D点的坐标(ω3，0.1η0)。当节点的轴向刚度下降到0.1η0时，该刚度与腹杆轴向刚度串联后的总刚度极小，结构已基本失去了承受荷载的能力，因而本文只讨论ω≤ω3时的节点轴向刚度。综上所述，需要拟合的参数为：η0、α、ω1、ω2、ω3。

3.2 腹杆受压时参数的回归分析

从前述分析看出，在腹杆受压时，参数τ0、β1、τ1、θ、σz/fy的变化对节点轴向刚度的影响较大，而参数i的改变对节点轴向刚度的影响较小。本文忽略参数i的影响，构造η0的多元回归公式如下：

η0=c0τ0c1β1c2τ1c3(sinθ)c4ec5σz/fy。

(6)

将式(6)两边进行对数运算，回归公式变成如下形式：

ln(η0)=lnc0+c1lnτ0+c2lnβ1+c3lnτ1+c4ln(sinθ)+c5σz/fy。

(7)

ln(η0)采用多元线性回归的方法拟合，拟合的系数见表7。根据表8对回归方程显著性检验：检验统计量F～Fα(p，n-p-1)，F分布表中F0.05(5,17)=2.81小于回归方程中的统计值，在显著水平α=0.05下认为回归方程是显著的，Pr反映大于t绝对值的概率，表示错误拒绝原假设的概率；回归方程的调整系数R2=0.97，回归方程在统计数值上来看是显著的。由表7对各回归系数显著性检验：检验统计量t～tα/2(n-p-1)，查t分布表tα/2(n-p-1)=t0.025(17)=2.11，小于本次回归统计值，Pr反映大于t绝对值的概率，表示错误拒绝原假设的概率。在显著水平α=0.05下可认为多项式ln(η0)回归系数是高度显著的。整理后，得到可接受的拟合方程为：