先整体后局部的铝合金车库节点受力分析

2019-09-2323

广西大学学报（自然科学版） 2019年4期

(1.广西大学土木建筑工程学院，广西南宁530004；2.工程防灾与结构安全教育部重点实验室，广西南宁530004;3.广西防灾减灾与工程安全重点实验室，广西南宁530004)

0 引言

铝是使用比较早的元素之一。通过冷加工，可以把铝强度提高一倍以上，也可以通过添加Mg，Mn，Si，Cu，Zn，Li，Ti等元素，进一步热处理强化，形成的铝合金既有优良的物理力学性能，又具有重量轻等优点，弥补了纯铝强度和硬度都很低的不足。沈祖炎等[1]对铝合金结构的研究现状进行了总结，铝合金结构应用十分普遍。石永久等[2-3]介绍了铝合金结构在建筑结构当中的应用，同时说明了铝合金材料没有屈服台阶，延伸率较小的特点。杨联萍等[4]研究了铝合金的空间网格结构的一些关键问题。郭小农等[5-6]对FRP材料加强铝合金结构的技术进行了探讨并对铝合金结构的螺栓连接在高温状态下的受力情况进行分析。郭小农等[7]进行了14根国产6061-T6铝合金挤压型材的受弯构件试验，系统地搜集了24个已有同类试验数据。罗翠[8]分析了铝合金网壳铸铝节点的受力性能，发现节点属于脆性破坏，需要加强螺栓孔处等薄弱部位。钱鹏等[9]研究了FRP-铝合金组合材料在建筑结构当中的应用。石永久等[10-12]研究了铝合金板件螺栓连接的承压强度和抗剪强度，并且对铝合金构件螺栓抗拉弯承载力进行了分析。DEMATTEIS[13]研究了铝合金T型连接件在不同力学参数下的受力特点。李静斌等[14]通过试验研究、理论分析和数值模拟解决了铝合金栓接节点承载力的计算。程明等[15]提供了铝合金构件连接的建议并对常见的连接方式提供了设计方法。COUGHLIN等[16]研究了在役公路桥梁在正常荷载状态下的铝焊缝的疲劳特性。

近年来，铝合金结构发展迅速，更是应用到承重结构中，例如立体车库(图1)、人行天桥(图2)等。铝合金结构较钢结构具有一定的优点[17]，如其在空气中形成一层质密的氧化膜，能够有效的防止金属腐蚀现象发生，确保了结构的强度。另外，铝合金的装饰效果好，且比强度高，有效抵抗地震荷载带来的影响，同时耐低温，在低温状态下强度有所增加且延性不降低，铝合金绿色环保[17]，容易回收再利用。然而，铝材弹性模量较低，结构相对较柔，因此其结构强度、刚度、稳定性及节点连接等问题亟待解决。

图1 铝合金车库
Fig.1 Aluminum structural garage

图2 铝合金人行天桥
Fig.2 Aluminum structural pedestrian bridge

本文以某小区的铝合金车库为研究背景，通过有限元分析其结构强度、变形，并对节点连接进行设计及验算。首先将车库框架进行整体分析，考虑最不利荷载组合[18](自重+车重+人荷载)，验算结构最大变形和强度是否满足要求；若对整个结构建立实体单元进行分析则会存在计算效率低下，在局部节点区域不精确等问题，为避免上述问题，通过圣维南原理对节点建模分析。研究表明，铝合金结构可以作为承重结构，本文所设计的节点连接形式在不利工况下满足强度和局部稳定要求，该分析方法对铝合金结构施工和设计的工程以及科研人员具有重要的参考价值。此外，铝合金结构相对钢结构较柔，耗能效果好。

1 立体车库结构布置

某车库主要由主梁、次梁、柱和车载板[19]组成，严格按照特种设备的规范要求进行设计，结构布置如图3。主梁跨度为5.5 m，次梁跨度为2.4 m，采用H型截面形式，柱高为2.6 m，采用空心方形截面形式，截面尺寸如图4所示。所有构件均采用6082-T6型铝材，弹性模量为68 000 MPa，泊松比为0.33，密度为2 700 kg/m3，材料设计强度为260 MPa。在主梁上面施加间距为5 m的车辆荷载，按照车重要求，车重限制为1.8 t，考虑活载，即施加20 kN的荷载，分为4个5 kN的集中荷载施加在车库主梁上(图3)。构件之间的连接均通过螺栓进行连接，本文主要对此进行设计和验算。

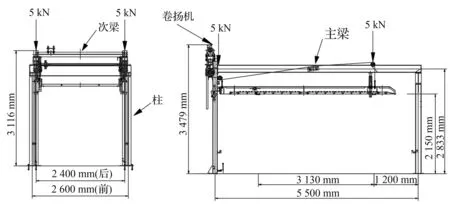
图3 铝合金车库设计图Fig.3 Aluminum garage design drawing

图4 截面形式Fig.4 Cross-section form

2 结构整体分析

2.1 基本理论

为了确保结构强度、稳定性和振动的安全性能，基于《铝合金结构设计规范》[20]对车库框架进行验算，其中包括变形、强度、抗剪强度、梁柱的整体稳定性计算。

①挠度验算，为结构和构件能正常使用，在设计时应对变形进行控制，对于主体结构的构件，受弯构件挠度的容许值为l/250，l为构件的计算长度。

②强度验算，强度验算主要分为受弯构件的强度验算和轴心受力的强度验算。对于受弯构件的强度，由于产生两个方向的弯矩，所以需要通过叠加判断是否超过材料强度的设计值：

(1)

其中，Mx和My分别为同一截面处绕x轴和y轴的弯矩值；Wenx和Weny分别为x轴和y轴的有效净截面模量；γx和γy均为截面的塑性发展系数；f为铝合金材料的抗弯强度设计值。对于受弯构件的抗剪强度有：

(2)

其中，Vmax为构件的最大剪力；S为毛截面对中和轴的面积矩；I为毛截面惯性矩；tw为腹板厚度；fv为材料抗剪强度设计值。对于轴心受力构件的强度有：

(3)

其中，σ为正应力；N轴心压力设计值；Aen有效净截面面积。

③稳定性验算，为了确保结构的稳定性，需要控制构件的长细比，对于受压构件需要满足的容许长细比为150；受弯构件的整体稳定可通过式(4)进行计算:

(4)

其中，Mx为最大弯矩；Wex为有效截面模量；φb为梁的整体稳定系数。

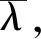
(5)

(6)

(7)

对柱的稳定性计算:

(8)

2.2 建模参数

将车库框架进行整体受力分析，利用ABAQUS建模得到524个梁单元，单元类型为B31空间梁单元并采用线弹性材料，分别在主梁的四个点施加大小为5 kN的集中荷载，并且考虑结构自重(见图5)。柱与地面为固支。构件之间均为绑定连接，计算结果见表1、表2和图6。其中，U1、U2、U3分别表示沿x、y、z轴的位移，UR1、UR2、UR3分别表示绕x轴、y轴和z轴的转角位移；S1、S2、S3分别表示沿x、y、z轴的内力，SF1、SF2、SF3分别表示绕x轴、y轴和z轴的弯矩。

图5 整体框架图
Fig.5 Overall framework

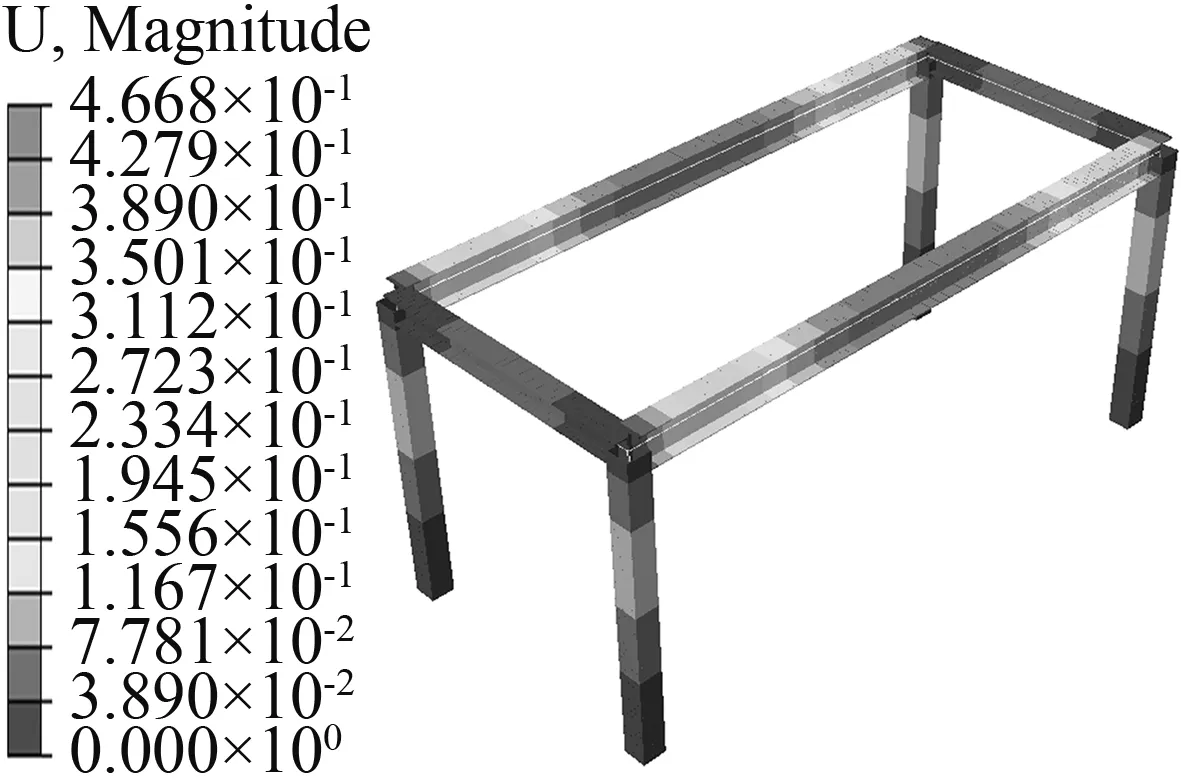
图6 框架变形图
Fig.6 Frame deformation diagram

表1 整体模型中X点、Y点和Z点的位移Tab.1 Displacement of X, Y, Z points inoverall model

表2 整体模型中X点、Y点和Z点的内力Tab.2 Section force of X, Y, Z points inoverall model

2.3 结果分析

2.4 车库振动分析

用ABAQUS软件建立B31梁单元模型，分析其自由振动行为，通过对振型图的分析，容易找出结构的薄弱点，通过结构动态分析优化结构设计。首先，计算车库在没有车辆荷载作用下的自由振动频率，计算结果如表3所示。

振型展示了结构的固有振动形态，提供了一种直观的分析结构振动状态的方法。通过自由振动振型图可以得出，是第一阶振型图(图7)和第三阶振型图(图9)显示了结构以该阶模态振动时，主梁跨中的侧向振幅最大，说明主梁横向刚度较弱，需要加强。第二阶振型图(图8)说明了次梁纵向振幅较大。第四阶振型图(图10)反映了主梁向内侧弯曲，依旧说明了主梁侧向刚度不足，可加厚翼缘和增加腹板。第五阶振型图(图11)体现了柱端整体侧移，主梁和次梁均发生刚体位移，而第六阶振型图(图12)显示柱端相互错动，使主梁发生扭转变形。由于对柱脚采用固支，所以柱脚部分均无变形。车辆荷载作用下，得到前六阶振动频率，结果如表4所示。

图7 自由振动第一阶振型图Fig.7 First-order vibration pattern of free vibration

图8 自由振动第二阶振型图
Fig.8 Second-order vibrationpattern of free vibration

图9 自由振动第三阶振型图
Fig.9 Third-order vibrationpattern of free vibration

图10 自由振动第四阶振型图Fig.10 Fourth-order vibration pattern of free vibration

图11 自由振动第五阶振型图
Fig.11 Fifth-order vibrationpattern of free vibration

图12 自由振动第六阶振型图
Fig.12 Sixth-order vibrationpattern of free vibration

表3 车库的自由振动频率Tab.3 Free vibration frequency of garage

表4 车库在车载作用下的振动频率Tab.4 Vibration frequency of garage under vehicle load

结果表明，在车辆荷载作用下的振动频率较低且相近，通过振型图(图13～图18)可以看出主要发生主梁的平面外失稳，所以需要增加主梁的侧向刚度。

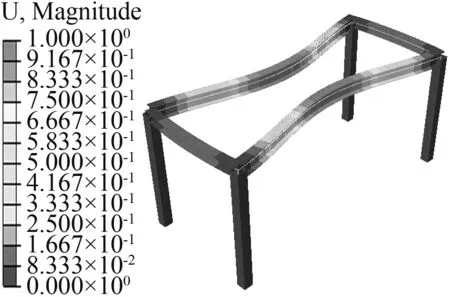
图13 荷载作用下的第一阶振型图Fig.13 First-order vibration pattern under the load

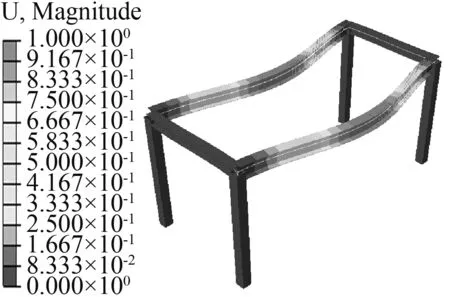
图14 荷载作用下的第二阶振型图
Fig.14 Second-order vibrationpattern under the load

图15 荷载作用下的第三阶振型图
Fig.15 Third-order vibrationpattern under the load

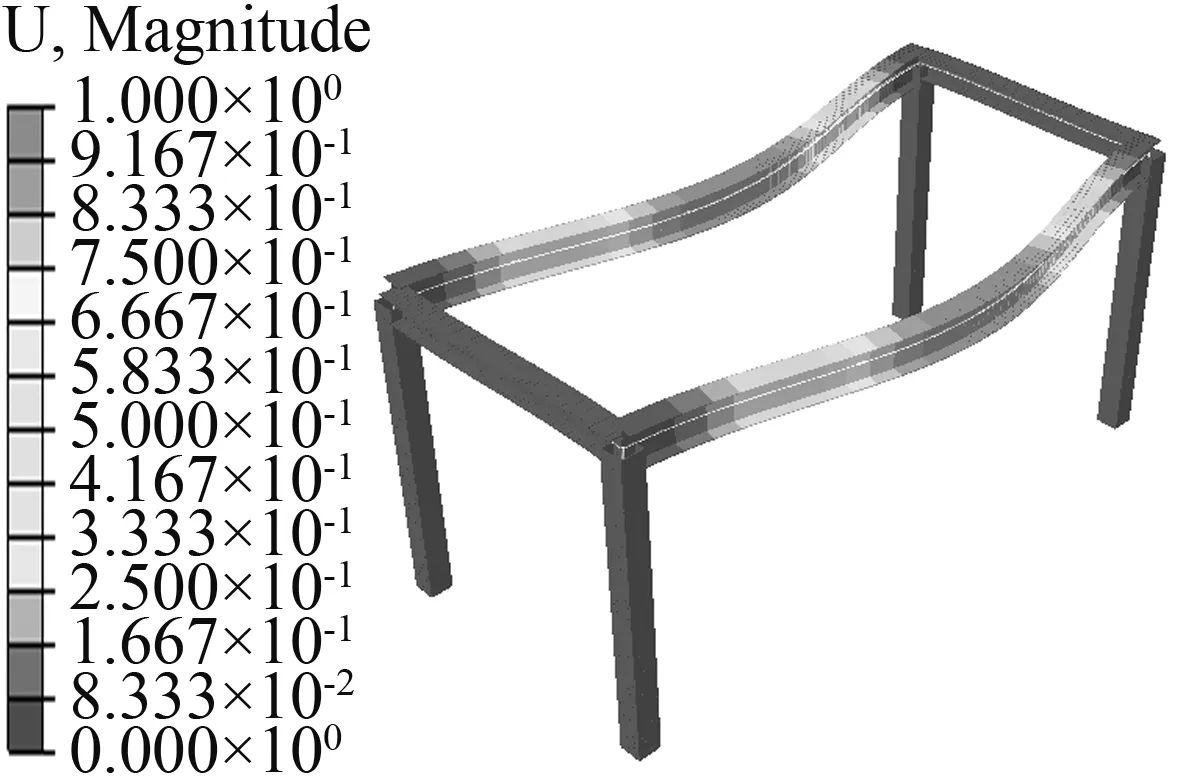
图16 荷载作用下的第四阶振型图Fig.16 Fourth-order vibration pattern under the load

图17 荷载作用下的第五阶振型图
Fig.17 Fifth-order vibrationpattern under the load

图18 荷载作用下的第六阶振型图
Fig.18 Sixth-order vibrationpattern under the load

3 节点有限元分析

3.1 局部分析方法

由于节点连接较为复杂性，采用圣维南原理进行局部分析，即将节点处沿x轴、y轴和z轴三个方向截取长度为L的截段并分别记三个方向的端点处为X点，Y点，Z点(图19)，在这三点施加力的边界条件或位移边界条件。

为了验证该方法的有效性，暂取L为1 m，进行建模计算。在整体模型中三点位移和内力如表1和表2。将整体模型中的三点位移和内力分别施加在局部模型当中，用B31空间梁单元建立节点处的模型,计算位移图见图20。

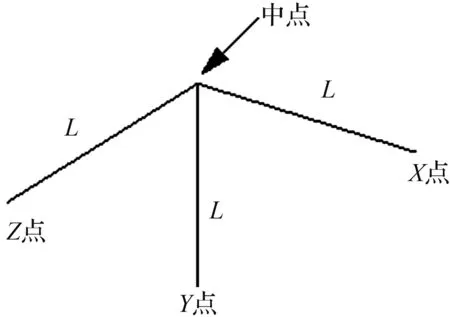
图19 节点局部
Fig.19 Node local

图20 节点分析
Fig.20 Node analysis

研究表明，先整体后局部的分析方法主要有以下两种：①以整体分析中的内力作为局部分析的外力，和结构相应位置的荷载共同作用。②以整体分析时得到的位移作为局部分析的位移边界条件，并把原来结构的荷载作用上去。上述两种方法得到的结果相同，本文采用第二种施加位移边界条件的方式分析节点处的应力情况。

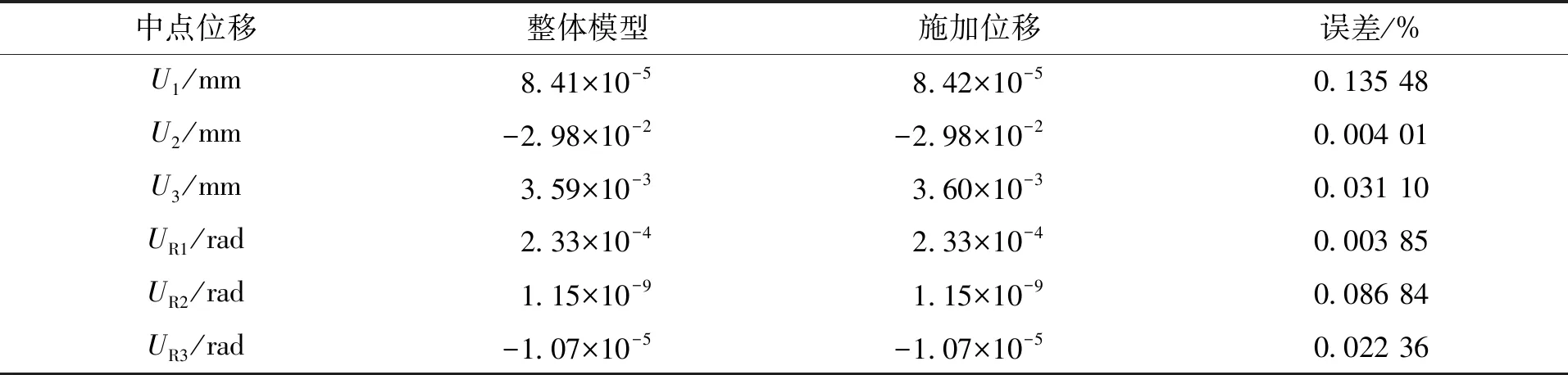
表5 施加位移边界条件和整体模型的中点处位移对比Tab.5 Compared between displacement boundary condition and overall model in joint’s displacement

表6 施加力边界条件和整体模型的中点处位移对比Tab.6 Compared betweenreaction force boundarycondition and overall model in joint’s displacement

3.2 节点设计和建模计算

节点连接形式主要以螺栓连接为主，由于铝合金材料的线膨胀系数为0.00002/°C，其对温度较为敏感，若采用焊接连接，焊接处的热影响区强度下降至设计强度值的1/3，故不宜采用焊接连接。其中与腹板连接的螺栓主要发生剪切变形，与柱连接的螺栓主要发生拉伸变形，所以为了使两者更好的协同作用，应按照规范[11]设计螺栓的位置和直径。为了满足强度要求及方便安装，梁柱节点连接尽可能简单且容易制作(图21)。某小区车库采用L连接件连接节点，L型连接件的厚度为10 mm，截面尺寸如图22所示。摩擦型高强螺栓连接，通过连接件和螺栓传递弯矩和剪力。

图21 L连接件连接节点
Fig.21 Connection of L connector

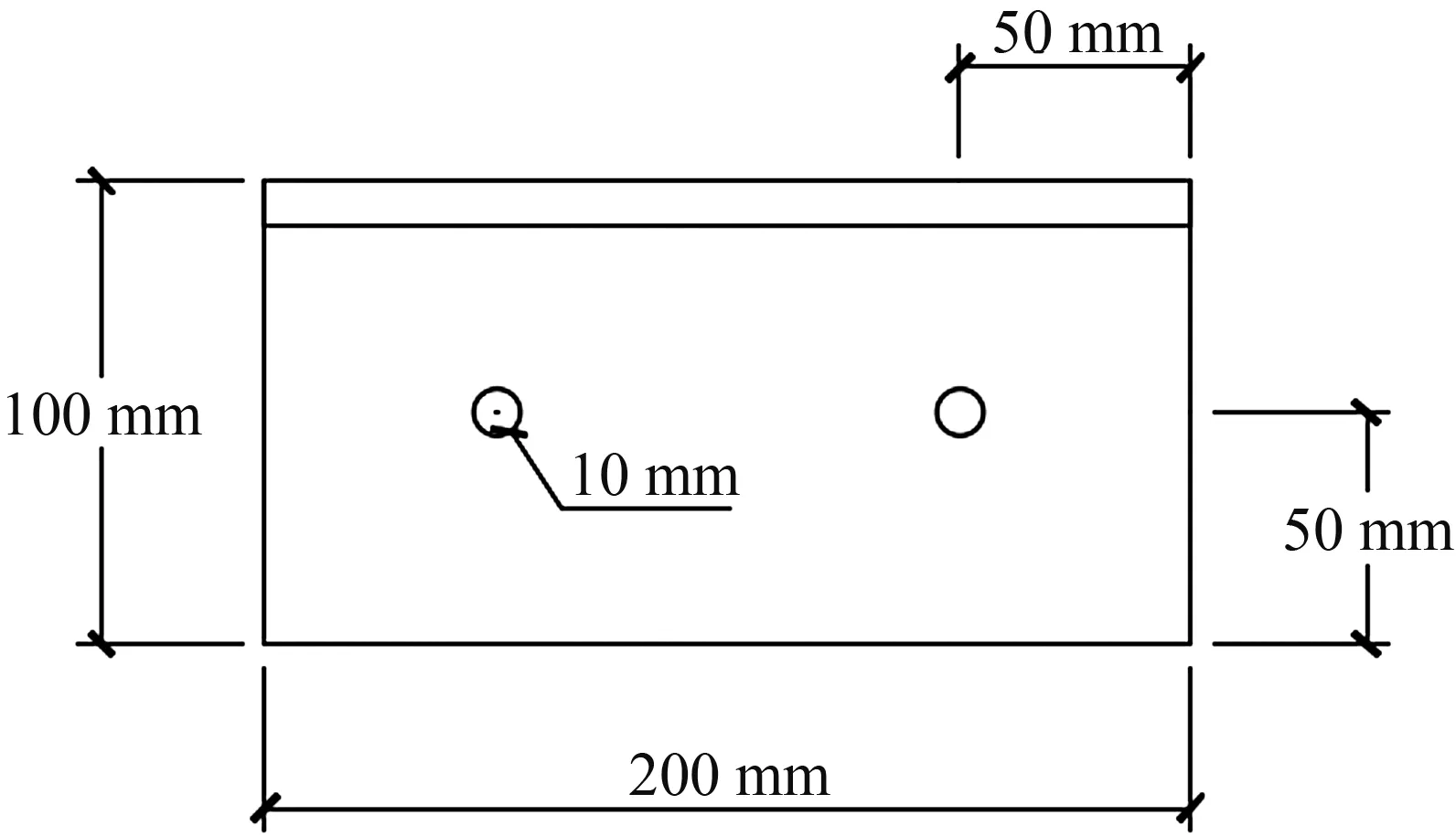
图22 L连接件
Fig.22 L connector

采用实体单元模拟节点处的局部应力状态。用C3D8R单元建立实体模型对节点区域进行局部分析(图23、24)，模型中实体包括主梁、次梁、柱、连接件和螺栓。将表1中的节点边界处的位移施加在梁端和柱端，另外施加原有位置的车辆荷载和自重。

其中，构件之间的接触设置为切向罚函数摩擦，摩擦系数为0.3，法向为硬接触，实体模型中共有63 188个实体单元，确保了有限元实体分析结果的准确性。

图23 有限元模型
Fig.23 Finite element model

图24 L型连接件
Fig.24 L-shaped connector

3.3 构件局部受力分析

计算云图为图25～28，其中图26、27、28即为沿x轴、y轴和z轴三个方向的主应力云图，从图中可以看出，构件沿x轴方向的主应力最大为27.62 MPa。出现在车辆荷载与构件接触处，并没有出现屈服现象，6082-T6型铝合金的屈服强度约为260 MPa。其他两个方向的最大主应力分别为：38.56 MPa和40.91 MPa。根据Mises屈服条件，可得σ=31 MPa<260 MPa。

图25 构件应力图
Fig.25 Component stress diagram

图26 构件x轴方向应力图
Fig.26x-direction stress diagram of component

图27 构件y轴方向应力图
Fig.27y-direction stress diagram of component

图28 构件z轴方向应力图
Fig.28z-direction stress diagram of component

对于局部应力超过设计强度的应予以加强，常用的加强方式有：加焊接肋板，增加构件截面的有效厚度，增设加劲肋，避免发生平面外屈曲现象。对于应力集中效应明显处改进局部构造，当结构局部应力较大时，可改变构件截面形式。

3.4 螺栓及连接件应力分析

螺栓初始时施加7 kN的预紧力，然后按照整体模型中的位移，设置边界条件，图29～32为螺栓群的应力图，其中图30、31、32为沿x轴、y轴和z轴三个方向的主应力图。其中x轴和y轴方向的主应力分别为：136.2 MPa和145.2 MPa，两者均小于高强螺栓的屈服应力。

沿z轴方向的主应力最大为163.5 MPa，出现在连接主梁和柱的螺栓群上，主要由结构受拉导致。说明此处结构受拉较大，可进行加强，增加螺栓数目，分担拉力。

图29 螺栓群应力图
Fig.29 Bolt group stress diagram

图30 螺栓的x轴方向应力图
Fig.30x-direction stress diagram of bolts

图31 螺栓的y轴方向应力图
Fig.31y-direction stress diagram of bolts

图32 螺栓的z轴方向应力图
Fig.32z-direction stress diagram of bolts

图33 连接件应力图
Fig.33 Joint group stress diagram

图34 连接件x轴方向应力图
Fig.34x-direction stress diagram of joints

图35 连接件y轴方向应力图
Fig.35y-direction stress diagram of joints

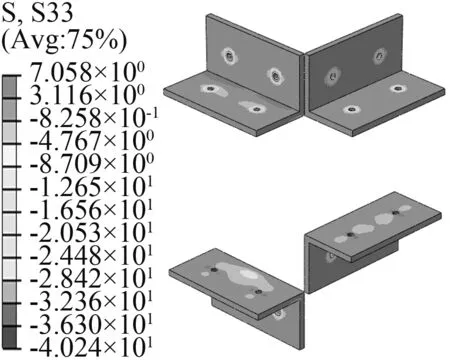
图36 连接件z轴方向应力图
Fig.36 z-direction stress diagram of joints

通过计算分析可知，图33～36为连接件应力图，连接件沿x轴、y轴和z轴三个方向的主应力大小分别为：6.82 MPa、7.26 MPa和7.06 MPa。其中，Mises应力为29.7 MPa，小于屈服强度，满足要求。螺孔和连接件拐角处应力偏大，可适当加厚或加肋，以减少应力在此处的集中现象。综上所述，建议修改构件尺寸如图37和图38所示。节点板厚度增加至20 mm，以便增加节点板的刚度；螺栓直径采用M16，且增加螺栓数目为8个，防止螺栓拉伸破坏；主梁截面翼缘增厚至16 mm，且增加至两个腹板，加强主梁刚度。