大跨正交正放钢空腹夹层板楼盖刚度分析

(贵州大学空间结构研究中心， 贵州贵阳550003)

0 引言

空腹夹层板楼盖是由上、下肋及剪力键节点域构成的新型楼盖，按空间布局可分为正交正放、正交斜放和蜂窝型等形式，该楼盖具有整体受力性能好、自重轻、节约层高等优点，可采用装配化施工从而节约工期，钢空腹夹层板和混凝土空腹夹层板在公共建筑和工业建筑中大面积被使用[1-2]，工程应用如图1所示。

(a) 钢结构标准厂房

(b) 贵州省老干活动中心

图1 空腹夹层板工程实践
Fig.1 Engineering practice of vierendeel sandwich slab

空腹夹层板楼盖被提出以来，相关正交斜放空腹夹层板的研究在不断的完善和发展。魏艳辉等[3-5]对实际工程中钢空腹夹层板拼装单元进行相关试验，论证了结构有较大的竖向刚度；姚玲等[6]研究了混凝土空腹夹层板性能，提出空腹夹层板常用高跨比为1/30～1/20,空腹夹层板表层板厚度取空腹夹层板高度的1/40～1/30等；孙涛等[7]研究了钢空腹夹层板等效剪切刚度分析，将连续化方法与有限元进行分析对比，得出采用连续化分析方法进行钢空腹夹层板结构的静力计算，具有很高的精度；姜岚等[8-9]考虑跨高比、空腹率、表层薄板厚度、边梁宽度等参数的影响，研究了大跨度空腹夹层板楼盖基于舒适度要求的动力特性分析。

在设计空腹夹层板楼盖时，多采用实用分析方法，即将空腹的上下肋等代为实腹的梁进行分析和计算，建立的模型称为等代模型。Abaqus、Ansys和Midas Gen等有限元软件对结构层的概念要求不高[10]，在分析空间结构模型时，不需要进行等代，可以按照实际情况建模并进行分析计算，建立的模型称为非等代模型。

目前，关于空腹夹层板楼盖等代模型与非等代模型差异的研究较少，本文针对大跨度正交正放钢空腹夹层板楼盖，建立大量等代模型与非等代模型，分析网格大小、空腹夹层板高度和刚度比对楼盖竖向刚度的影响，并将等代模型与非等代模型进行对比，旨在完善相关的理论以及为以后的工程实际提供指导。

1 钢空腹夹层板基本构造

钢空腹夹层板结构由车间焊接的T型钢为上、下弦的“双十字单元”，运往现场，在上、下弦弯矩最小处用高强螺栓连接形成楼盖整体，如图2所示，标注“o”号者为高强螺栓连接位置，钢管剪力键节点如图3所示。网格设计要求如下：①采用装配化施工，单元和杆件件进行焊接；②楼盖网格可以是方(矩)形且每边网格数n≥5；③材料为弹性材料，截面保持平面假定。

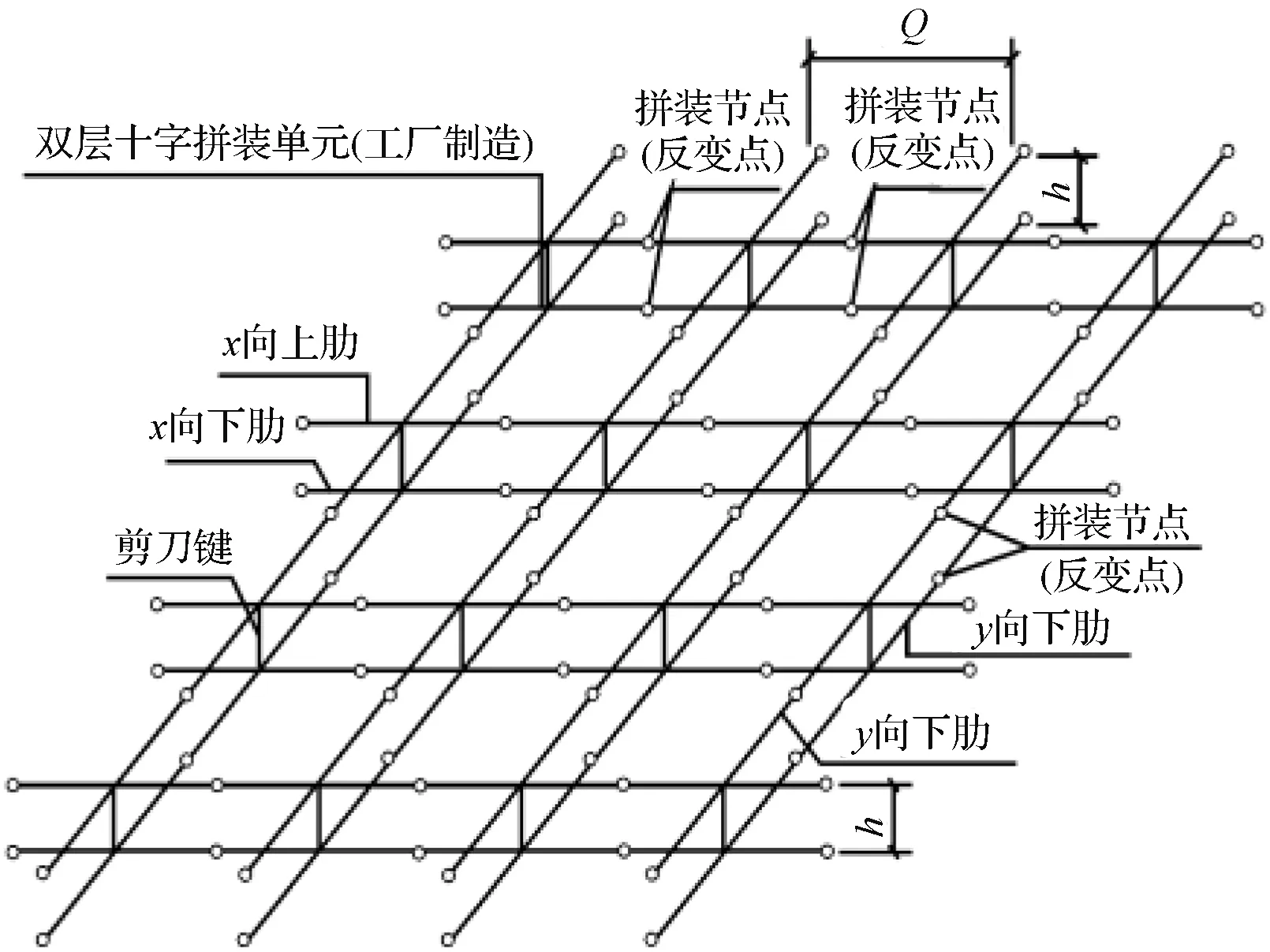
图2 钢空腹夹层板
Fig.2 Steel vierendeel sandwich slab

图3 钢管剪力键节点
Fig.3 Steel pipe shear key node

2 空腹夹层板楼盖的分析方法

2.1 实用分析方法——等效刚度法

等效刚度法将空腹夹层板看作空腹梁交叉组成，分析时考虑剪切变形的影响，基本假定如下[11]：①交叉的空腹梁上下肋变形后保持平面[12]；②正交网格短边数目大于5个，保证板网格的力学性能；③按照抗弯刚度等效原则。钢结构进行等效时，空腹夹层板对双T型截面形心轴的抗弯刚度E×I1等于H型钢对截面形心轴抗弯刚度E×I2，保持等效空腹夹层板总高度h，翼缘宽度b1，上下翼缘厚度tf、腹板壁厚tw不变，求等效刚度下H型钢的宽度b2，等刚度法示意图如图4所示，h1为上下肋高度。混凝土等效刚度法示意如图5所示，保持等效空腹夹层板总高度h，空腹梁与实腹梁高度h相等，求等代实腹梁的宽度bL为：

(1)

图4 钢结构等刚度法
Fig.4 Stiffness method of steel structure

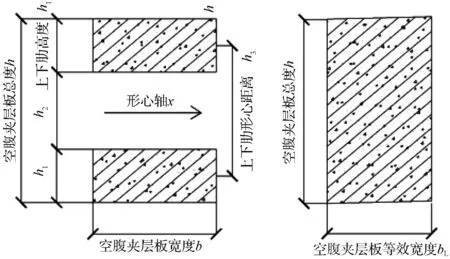
图5 混凝土等效刚度法
Fig.5 Concrete equivalent stiffness method

2.2 连续化分析方法

2.2.1 下表层等效板刚度

下表层无混凝土板，刚度为下肋的等代平面刚度。下肋由多组平面交叉杆系组成，则第i根杆的物理方程为：

(2)

式中：N为肋系轴力；E为肋系材料弹性模量；A为截面面积；u为位移；i为杆系序号。

假设投影与边跨角度为αi，则由弹性力学可得下肋轴向应变与平面应变的关系是:

εi=εxcos2αi+εysin2αi+εxysinαicosαi,

(3)

将式(3)代入(2)中得

(4)

式中：δi=Ai/li为杆系的折算厚度，li为杆系间距。

正交斜放网格，取αi=0°，则式(4)下表层板的刚度矩阵为：

(5)

其中：δx=Ax/Δx，δy=Ay/Δy；Ex和Ey是钢材弹性模量；Ax、Ay分别下肋x、y方向型钢截面面积；Δx、Δy分别为网格x、y方向肋的间距。

2.2.2 上表层板刚度

上表层板的刚度取上肋刚度与混凝土薄板的刚度的叠加，同时一般上肋与下肋的布置方式和采用的截面一致，因此上肋刚度可以取下肋刚度，故上表层板的刚度为：

Ba=Bb+Bc,

(6)

其中，混凝土板的平面刚度矩阵Bc为：

(7)

式中：μ为混凝土薄板材料的泊松比；Ec为混凝土材料的弹性模量；t为混凝土板的厚度。

2.2.3 基本方程建立

取拟夹层板的三个广义位移即挠度ω和转角ψx、ψy，为未知参量，依据弹性力学理论建立基本方程。

①几何方程。

(8)

其中：εa、εb表示为上、下表层的平面应变；χ、γ分别为拟夹层板的弯曲应变和横向剪切应变。

②物理方程。

(9)

其中：Na、Nb分别为上、下表层的内力；N、M、Q分别为拟夹层板整体的轴力、弯矩和横向剪力，具体可参见图6。

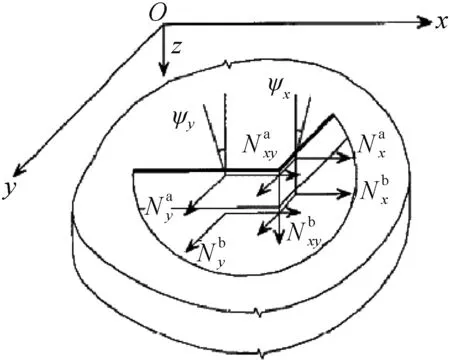
③平衡方程。

拟夹层板在竖向均布荷载作用下的平衡方程为：

(10)

方程的联立与求解请参看文献[11]的第2.5节。

3 结构建模与相关参数

本文建立大量非等代模型和等代模型，分别算出不同网格尺寸大小和不同空腹夹层板高度下，等代模型和等代模型的最大竖向挠度ω0和ω1，然后将等代模型中H型钢实腹梁的弹性模量乘以(1+β)进行调整，使ω1=ω0，定义β为刚度折减率，β为正时弹性模量增加，为负时减小。

3.1 构件尺寸

非等代模型构件截面尺寸：柱子为H 502×470×20×25，框架梁为H 900×300×16×28，层间梁为H 250×250×9×14，上、下肋为T 220×400×25×30，剪力键为圆形钢管400×20，截面尺寸单位为mm。与非等代模型相比，其他构件相同，等代模型没有剪力键，上、下肋按照等效刚度法等代为H型钢实腹梁，经计算，H型钢截面的宽度变化很小，取上、下肋宽度。非等代模型与等代模型分别如图7和图8所示。

图7 非等代结构模型示意图
Fig.7 Non-equal structure model diagram

图8 等代结构模型示意图
Fig.8 Equivalent structure model diagram

模型高度为4.2 m，平面尺寸为18 m×18 m，楼面均布恒荷载取3.5 kN/m2，均布活荷载取3 kN/m2。钢材的强度等级为Q345，弹性模量2.06×1011Pa。混凝土表层板的厚度为0.1m，混凝土强度等级为C30,弹性模量为2.98×1010Pa。在分析时，保持各构件截面尺寸不变。等代模型中，H型钢中间多出的自重，按均布线荷载反向施加H型钢梁上进行分析，空腹夹层板高度的不同，空腹夹层板高为0.6 m、0.7 m、0.8 m和0.9 m时，反向线荷载取值分别为q1=0.308 kN/m、q2=0.500 kN/m、q3=0.69 kN/m和q4=0.885 kN/m。

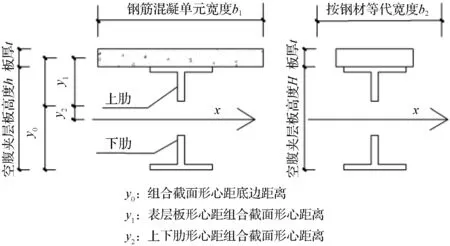
图9 刚度换算示意图Fig.9 Stiffness conversion diagram

3.2 刚度比

刚度比为混凝土板对组合截面形心[13]的刚度与上、下肋对组合截面形心刚度之比。计算时，保持楼板厚度不变，将混凝土弹性模量E1对应的单元宽度b1，按照钢材弹性模量E2进行等效得到等效宽度b2，等效板对组合截面形心y0的惯性矩Ix1，上、下肋对组合截面形心y0的惯性矩Ix2，此时定义刚度比[14-15]为C0=Ix1/Ix2，刚度换算示意图如图9所示。

3.3 夹芯层的等效剪切刚度

钢空腹夹层板楼盖等效的夹芯层等效剪切刚度需要先确定任一方向以及某一剪切单元的剪切刚度，然后根据各个方向的确定的剪切刚度确定夹芯层的剪切刚度。图10是取一方向以及一个剪切单元的原理示意图。采用拟交叉梁系法剪力剪切单元的剪切刚度，基本假定为：(1)只考虑钢梁翼缘6倍厚度范围内混凝土薄板的刚度作用；(2)剪力键截面相同；(3)上下肋的反弯点在节间的中点；不考虑扭转变形。

(a) 夹层板单元剪力图

(b) 夹层板单元弯矩图

(c) 等代梁单元剪力图

图10 等代梁元原理示意
Fig.10 Equivalent beam element method

由图10(a)，上下层肋的形心距离为h,网格长度为Δ，上肋组合截面刚度为E1×I1、下肋的截面刚度为E2×I2、剪力键的截面刚度为Ev×Iv；上肋的剪力为V1、下肋的剪力为V2，上下肋的轴力为H,等代梁元的总剪力为V，即V=V1+V2。由平衡条件得到:

(V1+V2)×Δ-H×h=0。

(10)

图10(b)为剪切单元弯矩图。由结构力学原理可以得到剪切变形γ0为：

(11)

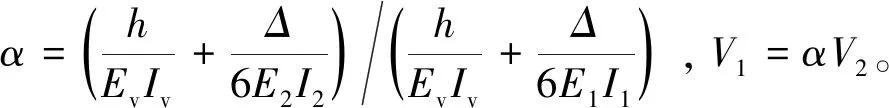
剪切单元的总剪切变形γ为：

(12)

因此，等代梁的剪切变形γ′为：

(13)

其中，C为剪切单元的等效剪切刚度，其表达式为:

(14)

对于双向的空腹夹层板，可以由拟夹层板法得到双向的正交斜放的夹芯层的等效剪切刚度为：

(15)

4 计算结果分析对比

4.1 组合截面形心与刚度分析

各个模型组合截面形心与刚度比的计算结果见表1。由表1可知，随着网格尺寸的增大，组合截面形心距底部的距离y0就越高，等效板对形心的惯性矩Ix1先增大后减小，上、下肋对形心的惯性矩Ix2逐渐增大，刚度比逐渐减小；随着空腹夹层板高度的增大，组合截面形心距底部的距离y0、等效板对组合截面形心的惯性矩Ix1和上、下肋对组合截面形心的惯性矩Ix2均增大，但刚度比逐渐减小。以上分析表明，混凝土板厚和构件尺寸截面一定时，随着网格尺寸和空腹夹层板高度的增加，上、下肋对组合截面的刚度贡献更大。

表1 形心位置与刚度比Tab.1 Centroid position and stiffness ratio

4.2 竖向最大挠度对比

不同网格尺寸下，非等代模型、等代模型以及H型钢弹性模量折减后的等代模型，跨中的竖向最大挠度[16]如图11所示。由图11可知，与非等代模型相比，网格尺寸为1.5 m时，空腹夹层板高度小于800 mm时，等代模型跨中的竖向最大挠度较大，大于800 mm时较小；网格尺寸为1.8 m时，空腹夹层板高度小于700 mm时，等代模型跨中的竖向最大挠度较大，大于700 mm时较小；网格尺寸为2.0 m和3.0 m时，等代模型跨中的竖向最大挠度均较小。网格尺寸小于2.0 m时，非等代模型的竖向刚度较强。

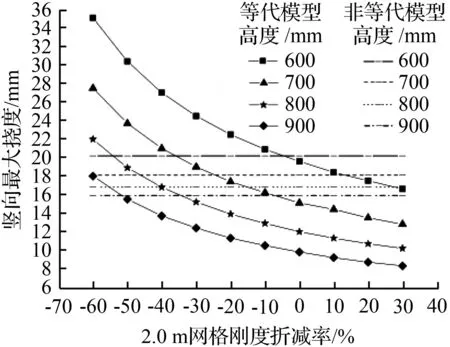
图11 竖向挠度
Fig.11 Vertical deflection

4.3 刚度折减率β分析

等代模型对H型钢实腹梁的弹性模量(1+β)进行调整，可以保证与非等代模型跨中的竖向最大挠度相等，折减率β与刚度比的关系曲线如图12所示，由图12可知，折减率β与刚度比呈正比，网格尺寸一定时，斜率为一个常数，网格尺寸越大，曲线的斜率就越小。折减率与网格尺寸的关系曲线如图13所示，由图13可知，折减率随着网格尺寸增大而减小，网格尺寸越大，H型钢弹性模量减少的就越多；空腹夹层板高度越大，H型钢弹性模量减少的就越多。

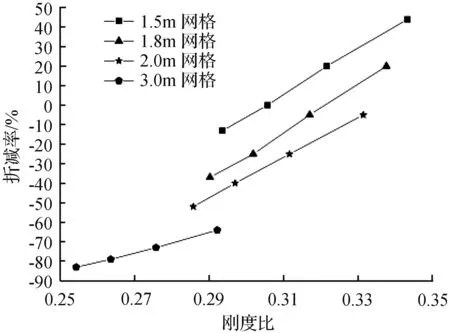
图12 折减率与刚度比关系曲线
Fig.12 Reduction rate and stiffness ratio curve

图13 折减率与网格长度曲线
Fig.13 Reduction rate and grid length curve

5 结论

①在截面一定的情况下，网格尺寸越大，混凝土板和空腹钢梁对组合截面的刚度贡献均增加，即E×Ix1和E×Ix2增大；在高度一定的情况下，随空腹夹层板的高度增加E×Ix1和E×Ix2也增大。但与空腹钢梁相比，混凝土刚度贡献的增大幅度较小，即刚度比减小。

②等代模型与非等代模型跨中最大竖向挠度值相差较大，产生的原因为等效刚度法可以保证抗弯刚度相同，但空腹夹层板网格上下肋的跨高比较小，抗剪刚度不能忽略，跨度越大，剪切刚度产生的挠度累计误差越来越大。

③网格尺寸小于2 m时，非等代模型的竖向刚度比等代模型要大；网格尺寸大于2m时，非等代模型的竖向刚度比等代模型要小；3 m时，等代模型的刚度折减率达到90 %，因此对于大跨度钢结构结构，建议网格尺寸不要大于3米。

④网格尺寸一定时，折减率β与刚度比C呈正比，斜率为一个常数，网格尺寸越大，斜率值越小；网格尺寸越大，H型钢梁的弹性模量折减的就越多。假定混凝土板厚度和截面保持不变，得到折减率β与刚度比C呈正比的定性关系，但之间的定量关系还需要理论和分析上的进一步研究并完善。