等螺距阶梯螺径螺旋宽幅摊铺布置研究
2019-09-23
(1.长安大学道路施工技术与装备教育部重点实验室, 陕西西安710064;2.陕西中大机械集团有限责任公司, 陕西西安710119)
0 引言
摊铺机螺旋输料器中的材料充满程度,对于摊铺均匀性有重要影响[1]。岳作强通过对螺旋输料器内混合料的充满程度稳定性分析,得出当料位系数为螺旋叶片直径的1/2时,混合料垂直输料方向的运动较强,离析趋势明显;当料位系数提高到螺旋叶片直径的2/3时,混合料开始形成不完整的半螺旋料流,离析趋势有所减弱;当料位系数提高到混合料完全埋过螺旋输料器时,离析现象得到显著的改善[2]。杨士敏等的研究表明,为了使螺旋输料器在布料过程中材料分布均匀、流动稳定,避免产生粗细材料颗粒分离现象,螺旋分料室中的料位系数应控制在螺旋叶片直径的4/5以上[3-4];还有一些研究资料认为,满埋螺旋输料更利于保证混合料的摊铺质量[5-6]。以上研究表明,螺旋中的料位系数大小对混合料离析有重要影响,随着料位系数取值增大,螺旋输料器内混合料的离析程度逐渐降低。摊铺作业时,螺旋输料器将混合料由中间输送到两边,材料流量由大到小逐渐变化。对于宽幅摊铺而言,螺旋输料距离长,流量变化大。若在全宽范围内采用同一直径的螺旋叶片,材料在宽度方向上不同位置,螺旋叶片的料位系数会有很大变化。料位系数越低,越容易产生材料离析现象[7]。
为了解决上述问题,李自光等提出了变螺径螺旋输料器满埋低速施工工艺,并进行了相关试验,证明变螺径螺旋输料器满埋低速施工是可行的[8];马登成等从螺旋输料器布料机理出发,进行了流体力学及运动学分析,认为采用变螺径变螺距螺旋进行摊铺作业可保证料流均匀性[9]。虽然使用变螺径变螺距螺旋可以改善摊铺质量,但是变螺径变螺距螺旋使用互换性差,加工生产也不方便,因此目前公路施工中均采用等螺距阶梯螺径螺旋叶片。为了提高摊铺质量,刘洪海建立了与螺旋结构参数、使用参数和材料参数相关的数学模型,通过分析各参数对螺旋布料器工作性能的影响,确定了料位处于不同高度的混合料状态[8]。在公路沥青路面施工技术规范(JTG F40—2004)中也对料位系数提出了建议,要求摊铺机螺旋输料器应保持有不少于2/3以上混合料,以减少摊铺过程中混合料的离析现象。
综上所述,螺旋输料器中的料位系数对输料过程中混合料的离析程度有显著影响,通常认为螺旋输料器中的料位系数越大,螺旋输料时混合料的离析程度越小。对于宽幅摊铺,由于材料流量沿宽度方向变化大,当不同直径的螺旋叶片配置方式不合理时,螺旋叶片的理论输料流量和该螺旋叶片位置处的实际输料流量不一致,就会导致输料过程出现缺料和堵料现象,使该螺旋中的料位系数过高或过低。当料位系数过低时,螺旋输料器中的混合料就容易离析,影响施工质量。故不同直径的螺旋叶片的配置方式对螺旋输料器的料位系数及施工质量有显著影响。本文通过对螺旋输料流量分析,建立输料流量公式,对阶梯螺径螺旋宽幅摊铺叶片配置进行研究;通过建立计算模型,导出在不同摊铺宽度条件下,满足流量系数要求的不同直径螺旋叶片的布置方案,为螺旋设计和工程应用提供参考。
1 建立螺旋输料流量公式
摊铺机稳定摊铺作业时,螺旋叶片在摊铺宽度上的输送流量应与对应位置的摊铺材料需要流量相等,该需要流量决定于摊铺速度、厚度、宽度与铺层材料密度。由于摊铺机在宽度方向左右对称,故只考虑摊铺宽度的一半进行研究。于是可得公式(1)[10]:
Q1=60(B-X)HcvγT,
(1)
式中,X为螺旋叶片到摊铺机中线的距离/m;Q1为位置X处螺旋叶片所需材料的理论流量/(t·h-1);B为摊铺宽度的一半/m;H为压实后的铺层厚度/m;c为松铺系数;v为摊铺速度/(m·min-1);γT为摊铺层材料虚铺密度/(t·m-3)。
定义材料在螺旋分料器直径方向所占比例为料位系数ξ,见式(2)所示,当ξ=1时为满埋螺旋状态,螺旋输料流量见式(3)[10]:
(2)
Q2=60FLJnLγLC1,
(3)
(4)
式中,h为实际料位高度/m;D为螺旋叶片直径/m;Q2为料位系数为1时螺旋叶片实际输料流量/(t·h-1);FL为料位系数为1时螺旋叶片输料面积/m2;J为螺旋螺距/m;nL为螺旋转速/(r·min-1);γL为螺旋输料器料槽中的材料密度/(t·m-3);C1为螺旋输料器流量修正系数(该系数与螺旋叶片直径有关);D0为螺旋轴径/m。

图1 物料速度分析图Fig.1 Analysisof material velocity
取螺旋面上任意点的物料为研究对象,对该点物料进行速度分析[11-16],见图1所示:
物料的轴向速度vz与径向速度vr之间的关系,见式(5)、(6)、(7)、(8):
(5)
(6)
(7)
μ=tanφ,
(8)
式中,r为物料与螺旋轴线之间的径向距离/m;β为位置r处的螺旋面升角/(°);φ为物料运动时与螺旋叶片的摩擦角/(°);μ为摩擦系数。
由式(5)、(6)、(7)、(8)得到式(9):
(9)
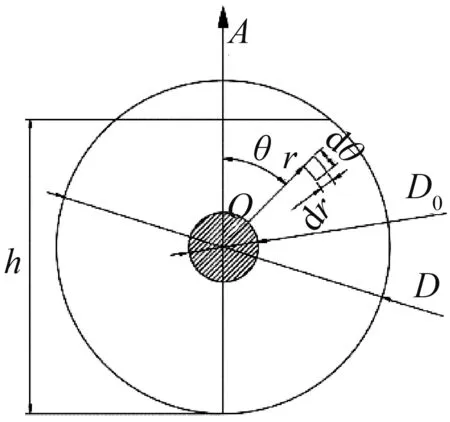
图2 螺旋输料流量计算示意图Fig.2 Diagramof spiral conveying flow calculation
为了建立螺旋叶片输料过程中的流量表达式,在叶片表面r、θ处取微元dr、dθ,见图2所示,可得料位系数与螺旋叶片的输料流量的关系,见式(10)、(11)、(12):
(10)
h=ξD,
(11)
Ω=f(h),
(12)
式中,Q2.0为料位系数为ξ时螺旋叶片的实际输料流量/(t·h-1),θ为微元dr、dθ与轴OA之间的夹角/°;Ω为实际料位高度为h时的输料区域面积/m2;f(h)为料位高度与输料区域面积之间的函数关系。
2 确定螺旋输料器流量修正系数
当料位系数为1时,由式(10)、(11)、(12)可得螺旋叶片的实际输料流量表达式,见式(13):
(13)
式中,Q2.1为料位系数为1时,考虑修正系数的螺旋叶片实际输料流量/(t·h-1)。将(13)与式(3)相比,可得修正系数C1,见式(14):
(14)
根据文献[8],通常μ取0.25,J取0.28 m,D0取0.1 m,于是C1与螺旋叶片直径D的关系,见图3所示:
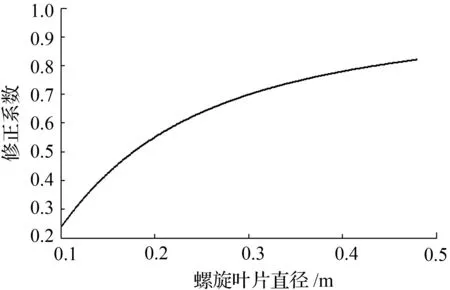
图3 输料器流量修正系数与螺旋叶片直径的关系Fig.3 Relation between the feeder flow correction coefficient and the diameter of the spiral blade
由图3可知,C1随D的增加而在增大,但增大的趋势在变缓,并存在极限值,该极限值可由洛必达法则求得,见式(15):
(15)
式(15)表明,当螺旋叶片的直径D足够大时,修正系数的极限值为1。
由图3可知,当0.1 m≤D≤0.3 m时,修正系数C1随螺旋叶片的直径D增加成非线性增大;而对于常用螺旋直径范围0.3 m≤D≤0.48 m,二者之间有近似线性关系,为了简化计算在该范围内对其进行线性拟合,得到式(16):
C1=0.52+0.65D。
(16)
采用拟合优度对拟合效果进行检验,计算公式见式(17):
(17)

由式(17)计算得相关系数R2=0.987,表明当300 mm≤D≤0.48 m时,C1与D有显著的线性相关关系。
将式(16)代入式(3),得到料位系数为1时,螺旋叶片实际输料流量公式,见式(18):
Q2=60FLJnLγL×(0.52+0.65D)。
(18)
3 不等直径螺旋叶片在摊铺机上的配置研究
为了便于分析计算,将料位系数换算为材料在螺旋输料器中的流量系数,两者之间的关系,见式(19):
(19)
式中,ω为材料在螺旋输料器中的流量系数。由式(19)可得流量系数ω与料位系数ξ的对应关系,料位系数ξ在积分区域Ω之中,见式(20):
(20)
式(20)表明,螺旋输料时流量系数ω与料位系数ξ之间的关系仅由螺旋的结构参数和摩擦系数决定,而与螺旋转速、料槽内的材料密度无关。当D分别取0.48 m、0.42 m、0.36 m、0.31 m;D0=0.1 m时,可得图4所示的曲线图:
图4中曲线表明,料位系数ξ随着流量系数ω的增大而增加。当料位系数取67 %,采用0.48 m,0.42 m,0.36 m,0.31 m的螺旋叶片输料时,对应的流量系数分别为69 %、67 %、65 %、64 %。当螺旋叶片的流量系数大于69 %时可以使各级螺旋叶片的料位系数大于66 %;为了便于计算,取各级螺旋叶片输料的流量系数均大于70 %。
对于采用0.48 m,0.42 m,0.36 m,0.31 m几种直径螺旋叶片的摊铺机,在满足材料流量系数大于70 %条件下,进行螺旋叶片的布置设计计算,螺旋在摊铺机上的安装位置如图5所示:
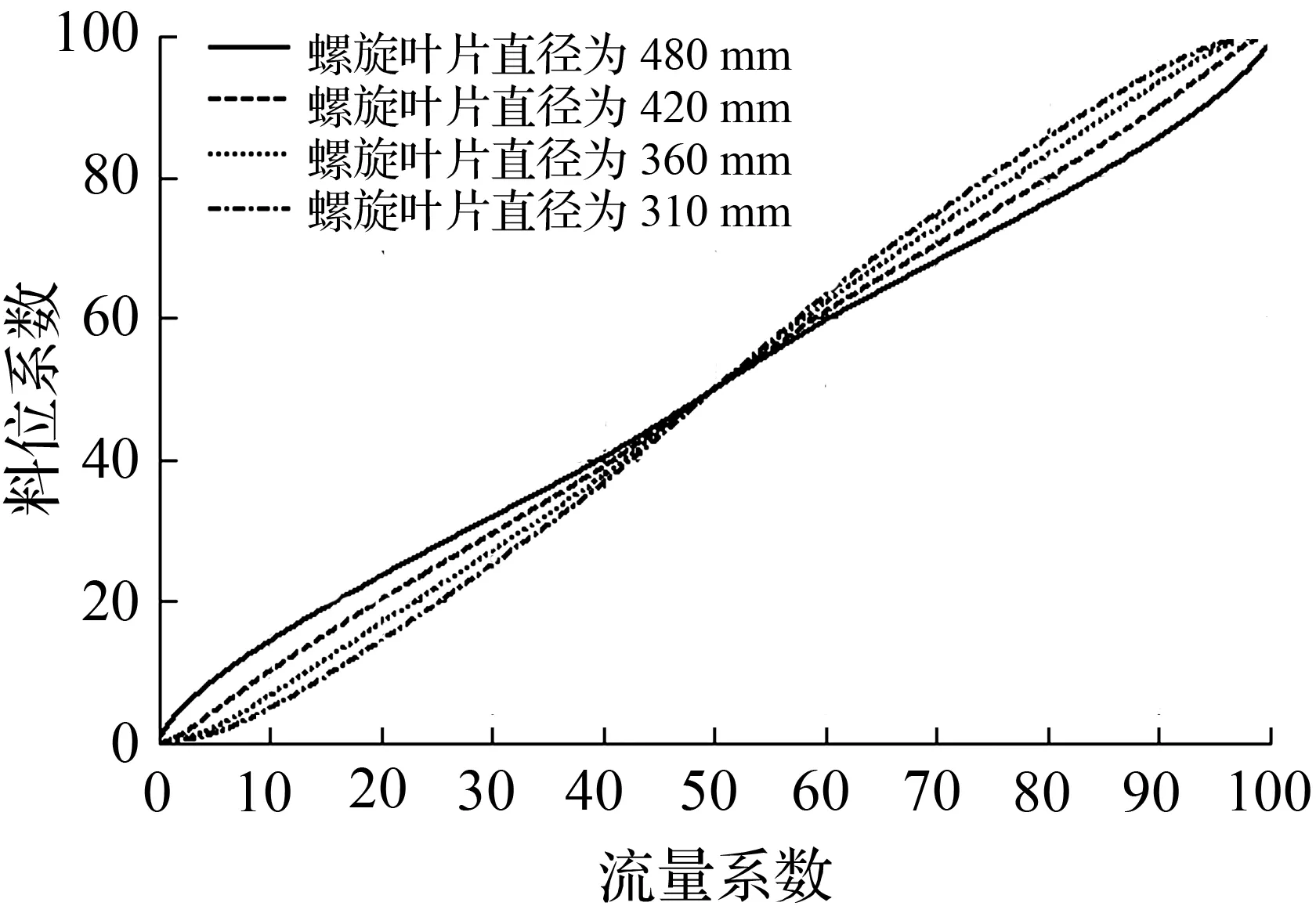
图4 流量系数与料位系数之间关系
Fig.4 Relation between the flowcoefficient and material level coefficient

图5 螺旋在摊铺机上的安装位置示意图
Fig.5 Schematic of screw installationlocation on the paver
图5中,直径为0.48 m,0.42 m,0.36 m,0.31 m的螺旋叶片采用阶梯布置,X1为流量系数为1时,0.48 m螺旋叶片离摊铺机中线的距离;X2为流量系数为1时,0.42 m螺旋叶片离摊铺机中线的距离,X3为流量系数为1时,0.36 m螺旋叶片离摊铺机中线的距离;X4为流量系数为1时,0.31 m螺旋叶片离摊铺机中线的距离。
对于阶梯直径螺旋叶片的布置问题,需要满足两个约束条件:(1)各级螺旋叶片输料的流量系数应大于70 %,即螺旋叶片流量系数的变化为满埋螺旋的±30 %;(2)由于螺旋端部到边板之间通常有0.5m到1m的预留宽度,因此螺旋端部叶片与摊铺机中线的距离介于(B-1)m~(B-0.5)m之间。以每级螺旋叶片流量系数变化量之和达到最小为目标函数,由式(1)知,位置X处螺旋叶片所需材料的理论流量与螺旋叶片的布置位置X为线性关系,故可建立整数线性规划模型,见式(21):
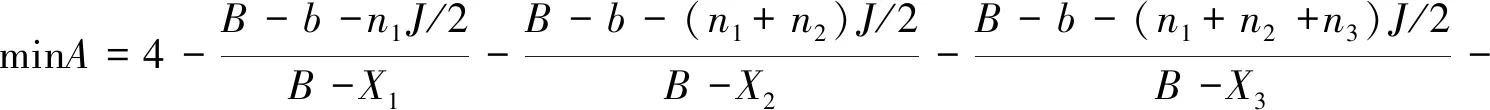
s.t.
(21)
上式中,A为螺旋叶片流量系数变化总和;D1,D2,D3,D4为螺旋叶片的直径(0.48 m,0.42 m,0.36 m,0.31 m);j为不同直径螺旋叶片的代号,取1,2,3,4;nj为直径Dj的螺旋叶片安装数量;k为螺旋吊臂个数,每个吊臂在螺旋轴向占用长度0.15 m。
根据条件(1),并由式(18)可得0.48 m螺旋叶片输料流量表达式,见式(22);此时由摊铺作业决定的实际需要流量,见式(23)。
Q11=60×1.3×FLnLJγL×(0.52+0.65D1),
(22)
Q21=60(B-b)HcvγT,
(23)
式中,Q11为0.48 m的螺旋叶片的实际料流量/(t·h-1);Q21为摊铺作业决定的实际需要流量/(t·h-1)。当摊铺机稳定工作时,螺旋叶片的布置位置处的理论料流量Q11应与实际料流量Q21相等,联立式(22)、(23),得摊铺速度、压实后的铺层厚度与螺旋输料器的转速之间的关系,见式(24):
(24)
以DT1800摊铺机宽幅(宽度12 m)摊铺为例,令B=6 m,D0=0.1 m,D1=0.48 m,b=0.68 m,γT=1.81 t·m-3,γL=1.56 t·m-3,J=0.28 m,c=1±0.3(取大值),得摊铺速度、压实后的铺层厚度与螺旋输料器的转速之间的关系,见式(25):
(25)
对于确定的铺层厚度H,v与nL有确定的对应关系。
将D1=0.48 m,D2=0.42 m,D3=0.36 m,D4=0.31 m分别代入式(18),并与式(1)、(25)联立,得X1=1.91 m,X2=3.06 m,X3=3.99 m,X4=4.61 m。
将X1、X2、X3、X4代入整数线性规划模型,k取2,通过LINGO软件进行求解,得到n1=11,n2=9,n3=6,n4=4。即0.48 m的叶片使用11片,0.42 m的叶片使用9片,0.36 m的叶片使用6片,0.31 m的叶片使用4片,按叶片直径由大到小阶梯布置。
由式(25)及X1,X2,X3,X4计算分析可知,摊铺厚度、螺旋转速和摊铺机速度的比值为一个定值,因此螺旋叶片的布置仅决定于摊铺宽度,即只有摊铺宽度改变时,才需要改变螺旋叶片的布置方案。
对于宽幅摊铺,当宽度从9 m变化到12 m时,取0.5 m为一个摊铺宽度步长,按式(21)所示的模型进行求解,得到的螺旋叶片布置结果,见表1:
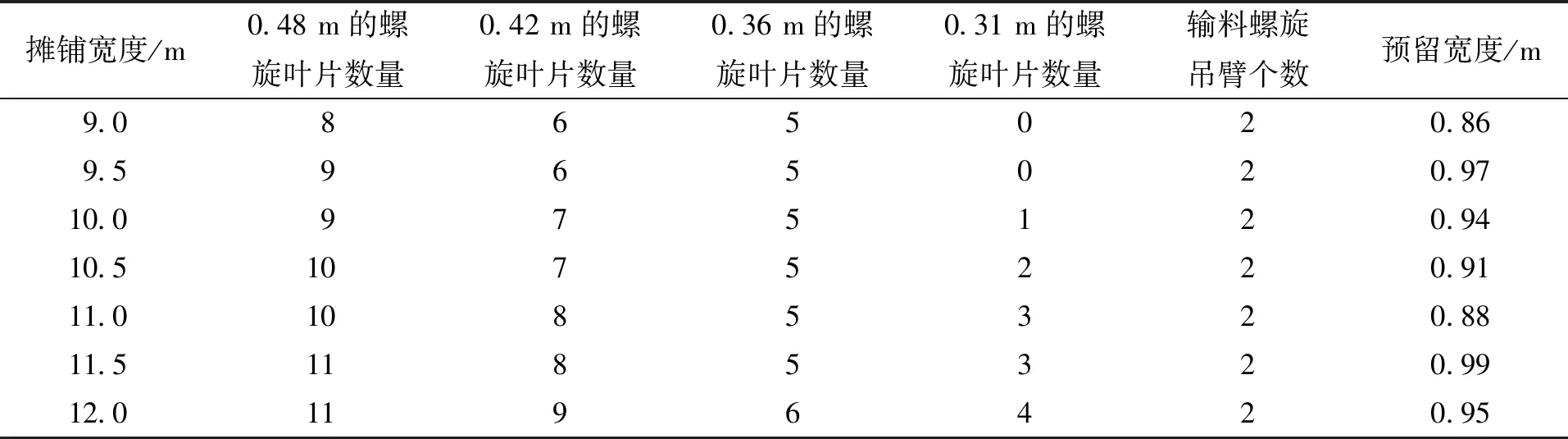
表1 不同摊铺宽度的螺旋叶片布置情况Tab.1 Spiral blade layout of the different paving width
从表1可知,当摊铺宽度发生改变时,螺旋叶片的布置方式要随之改变,每一级螺旋叶片的具体数量与摊铺宽度有密切的关系。
4 试验研究
4.1 试验材料
为了验证以上研究结论的合理性和有效性,在广西某高速公路采用DT1800型摊铺机进行AC25沥青混合料摊铺作业,混合料级配组成见图6。
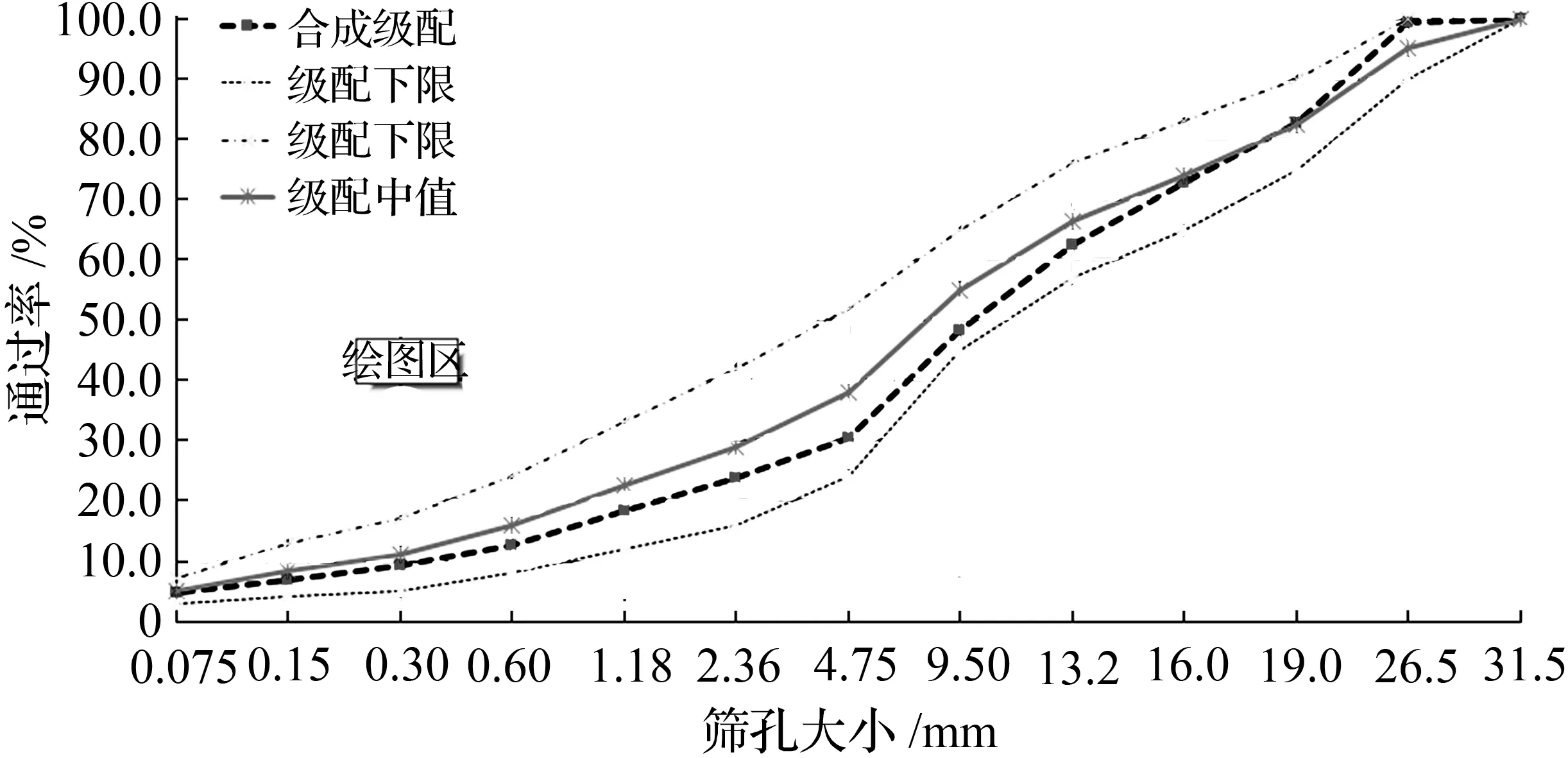
图6 混合料级配组成Fig.6 Composition of mixture gradation
4.2 试验装置
路面横断面宽11.75 m,摊铺厚度8 cm。摊铺机左侧螺旋布料器为等螺距等螺径螺旋,螺径为0.48 m,螺距为280 mm,螺旋轴直径100 mm;右侧螺旋布料器为阶梯螺径等螺距螺旋,螺径分别为0.48 m、0.42 m、0.36 m、0.31 m,螺距为280 mm。试验采用的等直径螺旋,见图7所示;阶梯直径螺旋,见图8所示。

图7 试验所用等直径螺旋
Fig.7 Test for the use of equal diameter spiral

图8 试验所用阶梯直径螺旋
Fig.8 Test with stepping diameter spiral

图9 检测现场Fig.9 Test site
4.3 试验方案
在摊铺过程中调节物料料位,当流量系数分别为1/2、2/3、1时进行试验。图9为利用无核密度仪检测路面密实度现场。数据采集时,沿摊铺方向,在所检测的路段上以1 m×1 m的方格网作为检测单元;纵向检测长度为40 m,横断面检测宽度11 m(路面两侧分别除去0.375 m)。考虑到试验路段摊铺机左右螺旋参数不同,会影响中间分界位置的材料状态,在检测结果中除去最中间1 m处的数据,得到400个检测值,见图10所示。

图10 检测区域示意图Fig.10 Diagram of detection area
4.4 试验结果
采用检测路段无离析区域的平均密度与离析处密度差的绝对值作为沥青面层集料离析的判定指标。经测定无离析区域的平均密度为2 318 kg/m3,参照离析判定标准(见表2所示)[17-18],判定检测点的离析程度,并进行统计分析,得出不同离析程度的点数及所占的比例,检测结果见表3和图11。

表2 离析评定指标Tab.2 Segregation Assessment Indicators
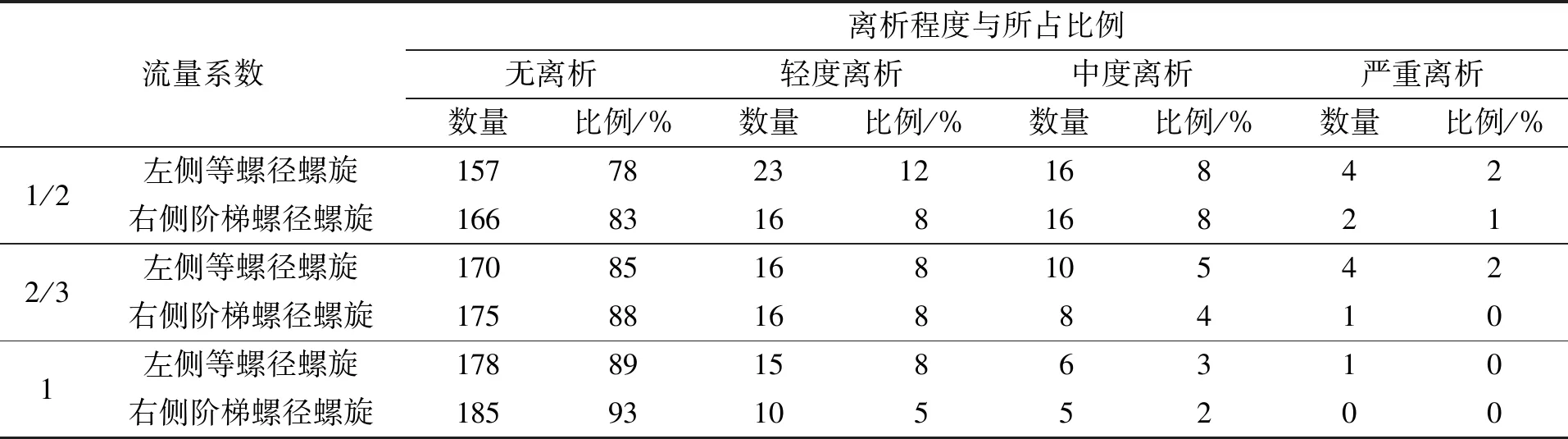
表3 离析检测结果Tab.3 Segregation test results
注:表中螺旋的螺距均为280 mm
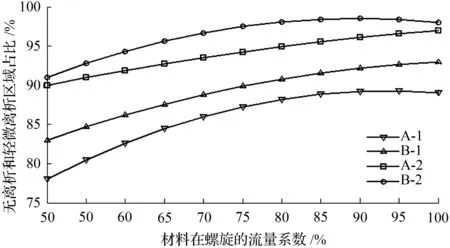
图11 螺径、材料流量系数与离析之间关系Fig.11 Relations between spiral diameter, flow coefficient and segregation
图中:A-1为等螺径螺旋与无离析区域关系曲线;A-2为等螺径螺旋与轻度加无离析区域关系曲线;B-1为阶梯螺径螺旋与无离析区域关系曲线;B-2为阶梯螺径螺旋与轻度加无离析区域关系曲线。
试验结果表明:①在各种材料流量系数下,阶梯螺径螺旋摊铺层的抗离析程度均高于等螺径螺旋。②随着材料流量系数增加,抗离析的能力均提高;在流量系数低于70 %时,提高的较快;在流量系数高于70 %时,提高的较慢。③无论是等螺径螺旋,还是阶梯螺径螺旋,均在流量系数为1时,抗离析的能力达到最佳值。
5 结论
为了解决等螺距阶梯螺径螺旋叶片的安装位置问题,建立了螺旋叶片输料能力模型、整数线性规划模型,确定了螺旋叶片的安装方案,并进行了试验验证,得出以下结论:
①摊铺机采用等螺径螺旋叶片进行大宽度输料时,材料的离析程度随着螺旋叶片流量系数的降低而增大;当流量系数小于70 %时,容易使旋输料器产生材料分布不均匀、流动不稳定、粗细材料颗粒分离现象。因此,需采用阶梯螺径螺旋,以满足摊铺过程对料位系数的要求。
②在摊铺机作业时,不同螺径螺旋叶片的布置位置与摊铺厚度、摊铺速度、螺旋转速无关,仅决定于摊铺宽度;通过建立整数线性规划模型,得到了摊铺宽度与等螺距阶梯螺径螺旋叶片布置关系,可为摊铺机螺旋输料器设计提供理论指导;基于该模型提出了与摊铺宽度相应的等螺距阶梯螺径螺旋叶片的安装布置方案,可为工程施工中螺旋叶片的合理布置提供依据。
③本研究中仅就工程中常用的四种螺径叶片,在宽幅摊铺中的布置情况进行了研究,未将螺径尺寸和叶片种类作为变量,在进一步的研究中应建立多因素模型,以期得到更全面的研究结论。
