基于黏着—犁沟摩擦理论的黏性土与混凝土界面受力试验与分析

2019-09-23

广西大学学报（自然科学版） 2019年4期

(青岛理工大学土木工程学院，山东青岛266033)

0 引言

研究黏性土与混凝土界面的受力特点有利于静压桩工程实际应用。目前国内外学者对黏性土桩界面的摩擦特性进行了相关试验研究，唯象的论述较多尚未形成系统的理论。

郭进军等[1]利用粗糙度测定仪，测定混凝土表面粗糙度，并利用曲面拟合法与测点数据平均法进行比较，为桩土界面粗糙度确定提供了可靠依据；张明义等[2]对原状土、重塑土与混凝土界面滑动摩擦进行比较，认为滑动摩擦力与土的类型、法向应力有关，可以将沉桩时的桩侧土当作原状土看待，用扰动土做滑动摩擦试验可以等同于原状土；石熊等[3]利用直剪仪进行不同粗糙度混凝土与红黏土界面试验，随着混凝土面粗糙度增加，黏聚力增大，破坏时的界面抗剪强度增大，界面残余强度也增大，但内摩擦角减小；BASU等[4-5]采用双表面塑性模型进行有限元模拟，分析了砂土及黏土中桩的侧阻力变化与相关文献中数据吻合良好；陈俊桦等[6]在不同粗糙度的混凝土与红黏土界面进行直剪试验，认为接触表面粗糙度存在阈值和粗糙度的影响范围有限值。

目前，桩—土摩阻力的研究仍以传统的库仑摩擦理论为基础。库仑摩擦理论无法对静压桩施工中的一些现象作出有说服力的解释，例如静压沉桩过程中出现的桩侧阻力退化效应以及沉桩力的时效性，但是从摩擦学理论出发，就可以得到比较合理的解释。

仅有少数学者根据摩擦学已有理论进行研究，汤连生等[7]在2004年引入摩擦学内、外摩擦的概念对土体间内摩擦及土体与混凝土界面的外摩擦分析界面摩擦机理。宋兵[8]在2010年引入现代摩擦学的观点将桩侧摩阻力分为黏着力和摩擦力二项；胡永强等[9]在2015年引入了目前趋于成熟的黏着摩擦机制和变形摩擦机理的宏观摩擦理论，为桩的侧摩阻力的研究提供了一条新途径。

笔者认为根据摩擦学黏着—犁沟摩擦理论能够很好的解释土体、混凝土—土直剪试验曲线成因，进一步阐明桩土界面细观受力问题，搭建宏观界面受力与细观颗粒受力之间的桥梁，对界面强度的解释明显优于库仑强度理论，有助于揭示静压桩的沉桩机理，具有重要意义。

1 黏着—犁沟摩擦理论

摩擦是两个相互接触的表面产生滑动或滚动时所遇到的阻力。摩擦现象并不是由单一因素控制，早期的机械互锁(啮合)理论、分子吸引理论[10-11]在特定的范围内能够较好的解释摩擦现象。但把摩擦解释为单一因素的影响是片面的并不能很好的适用于桩土界面。

鲍顿和泰伯(F P Bowden and D Tabor)在1950提出以黏着—犁沟理论[12]为现代固体摩擦奠定了理论基础。该理论以机械—分子联合作用为基础，能够很好的适用于桩土界面。

1.1 基本概念

在荷载作用下，两微凸体表面接触点因压力过大而发生塑性变形将接触点牢固黏着为一体，称为黏着。当发生黏着现象后，两微凸体表面产生相对滑动时，黏着点发生剪切破坏，剪切力就是摩擦阻力中的黏着阻力。

在两种软硬程度不一的微凸体表面接触后产生相对滑动时，硬微凸体峰点会在软微凸体表面产生犁沟，微凸峰点处犁沟的阻力就是摩阻力的另一组成部分即犁沟力。

黏着—犁沟摩擦理论将摩擦力的来源分为了两个部分，即黏着阻力与犁沟阻力，摩擦阻力可用下式表达：

F=T+Pe，

(1)

式中：F为摩擦阻力，T为摩擦阻力中的黏着阻力，Pe为摩擦阻力中的犁沟阻力。

1.2 表面间相互作用

1.2.1 黏着作用

两微凸体接触点的实际接触面积只是名义横截面积的很小一部分。这就造成接触点处的应力达到屈服强度σs而发生塑性变形，实际接触点在压应力的作用下牢固黏着。若荷载增大，因接触点的应力已经达到屈服强度，只能通过增加实际接触面积来承受荷载的增量(如图1中的A、C点)。

微凸体表面相对滑动的过程中，黏着点将会不断地剪断，新的黏着点也将会不断地形成，滑动过程中随着新旧黏着点的交替，黏着点的总黏着面积保持不变。

图1 黏着—犁沟摩擦示意图Fig.1 Adhesion and ploughing Sketch

1.2.2 犁沟作用

在两微凸体表面相对滑动时，犁沟微凸接触点可能会发生多种材料迁移现象，这跟软硬微凸体的材料特性有关。如图1中的犁沟微凸体B(或A)：

①微凸体B(或A)通过D时，微凸体D发生比较严重的塑性变形而黏着。若硬介质与软介质间黏着强度比软介质自身黏着强度大，则滑移剪断发生在软介质层内，从而造成软介质从下表面转移到上表面(D点被犁削后黏着于B点右侧，甚至填平微凸体B)。

②微凸体B(或A)通过D时，微凸体D虽然发生塑性变形，因硬介质与软介质间黏着强度比软介质自身黏着强度小，软硬介质间黏着并不牢固(D点被犁削后无法黏着于B点)。微凸体B(或A)沿D“犁削”而过，即沿两物体的界面剪断，这时下表面微凸体D发生材料迁移变形(犁沟)，但不发生转移情况。

③微凸体D只发生弹性变形，微凸体B(或A)比较容易地滑过D。

1.3 黏着—犁沟计算公式

摩擦力是黏着效应和犁沟效应产生阻力的总和。故摩擦力F的组成可表达为：

F=T+Pe=Ar·τb+S·pe,

(2)

其中，T为黏着力，T=Ar·τb，Ar为实际接触(黏着)面积总和；τb为黏着结点的剪切强度；Pe为犁沟力，Pe=S·pe；S为各犁沟点犁沟面积总和；pe为两界面间单位面积的犁沟力。

2 利用黏着—犁沟理论对黏性土—混凝土界面受力分析

根据黏着—犁沟理论黏性土—混凝土界面剪切力由黏着力及犁沟力提供。在相同条件下，黏着力的大小根据法向压力变化造成黏着面积的变化而随之变化；犁沟力的大小根据表面的粗糙程度不同而变化。根据黏着—犁沟理论，相同法向力作用下黏性土—混凝土界面的试验(反向剪切试验)可以保证黏着力不变而仅改变犁沟力；相同法向力作用下黏性土—混凝土界面的不同粗糙度试验[13]也可以达到相同的效果。根据这两种试验可以验证黏着—犁沟理论在黏性土—混凝土界面应用的正确性。

2.1 黏性土—混凝土界面切向力的组成

2.1.1 黏性土与混凝土反向剪切试验

文献[14]通过自制的单剪仪进行黏性土—混凝土界面反向剪切。其定义了“正向剪切比θ”为“先前施加的正向剪切应力与该法向应力下的接触面抗剪强度之比”。θ=1.0表示正向剪切已达破坏状态，θ=0表示没有经历正向剪切，当θ在0～1之间表示破坏的程度逐渐增强。先进行1组试样的正向剪切破坏，以确定特定法向力下的剪切强度。反向剪切的位移初始点为正向剪切时剪切力达到预设正向剪切比时的位置。

记录反向剪切力与位移值绘制曲线，从图2可以看出，对于θ=0的曲线在剪切初始阶段及后期均明显高于θ=1.0的曲线。根据黏着—犁沟理论公式(4)，在正向剪切时黏着力与犁沟力共同作用产生切向摩阻力；不改变混凝土板与黏性土的特性情况下，黏着结点的剪切强度τb和单位面积的犁沟力pe不改变；法向力不变，黏着面积Ar不会改变；这表明θ=0曲线高于θ=1.0曲线的部分为犁沟力Pe变化部分，即是犁沟面积的改变造成界面阻力的下降，如式(3)所示。正向剪切时硬微凸点在软介质上产生犁沟并使软介质微凸点发生迁移，反向剪切时硬微凸点沿已产生的犁沟反向移动不能发生接触，即无法产生犁沟力，这就是反向剪切摩阻力下降的原因。

F↓=T→+Pe↓=Ar→·τb→+S↓·pe→

(3)

需要注意的是，反向剪切摩阻力仍然包含犁沟力，因为反向剪切时仍然存在正向剪切时未发生迁移的犁沟微凸体接触点和软介质迁移后重新构成的微凸点，这两种微凸点均提供犁沟力。

库仑抗剪强度公式对反向剪切造成抗剪强度降低的解释只能是内摩擦角下降，无法利用其进一步分析颗粒级别的现象。

(a) 法向力应力22 kPa

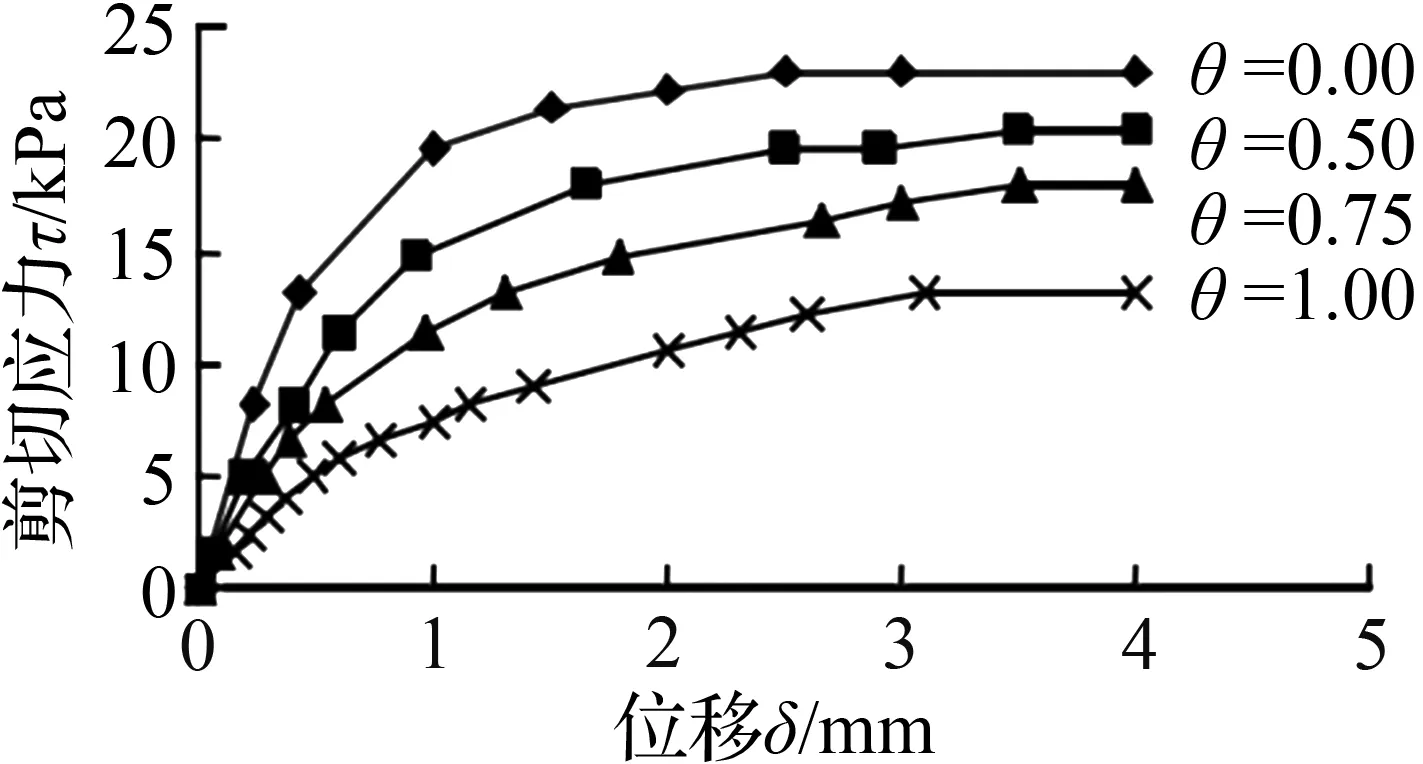
(b) 法向力应力42 kPa

图2 反向剪切应力—位移曲线
Fig.2 Stress-strain relationship in negative shear

2.1.2 黏性土与混凝土齿板剪切试验

根据黏着—犁沟摩擦理论所提出的摩擦力公式(2)，特定界面粗糙度变化的本质是黏着面积与犁沟面积的变化。两种材质相同而剪切面轮廓不同的界面相接触时，外轮廓的变化对单位面积上的犁沟力、黏着结点的剪切强度没有影响，但外轮廓的变化改变了剪切面的黏着面积及犁沟面积。

笔者通过混凝土齿板峰—谷距的变化改变黏土与混凝土界面的黏着面积及犁沟面积。设置4组混凝土齿板(图3)，其峰—谷距0 mm、2 mm、4 mm、6 mm分别编号Ⅰ、Ⅱ、Ⅲ、Ⅳ，峰—谷距2mm时如图4所示。

图3 混凝土板
Fig.3 Concrete plate

图4 混凝土齿板
Fig.4 Concrete toothed plate

通过直剪仪分别试验了有效法向应力23.6 kPa、43.2 kPa、88.7 kPa、142.8 kPa作用下黏性土与各混凝土齿板的剪切性能[15]。试验用土按照土工试验标准方法测定粉质黏土的物理力学指标，如表1所示。

表1 土的物理力学指标Tab.1 Physical and mechanical indexes of soil

根据图5相同粗糙度下法向力对剪切—位移曲线可知，相同表面特性的黏性土—混凝土界面在不同法向力作用下，界面摩阻力随法向力增加而增加。根据直剪试验回归得到的抗剪强度线图6可知，相同表面特性下黏性土—混凝土界面法向力与摩阻力线性增加。

(a) Ⅰ粗糙度板

(b) Ⅱ粗糙度板

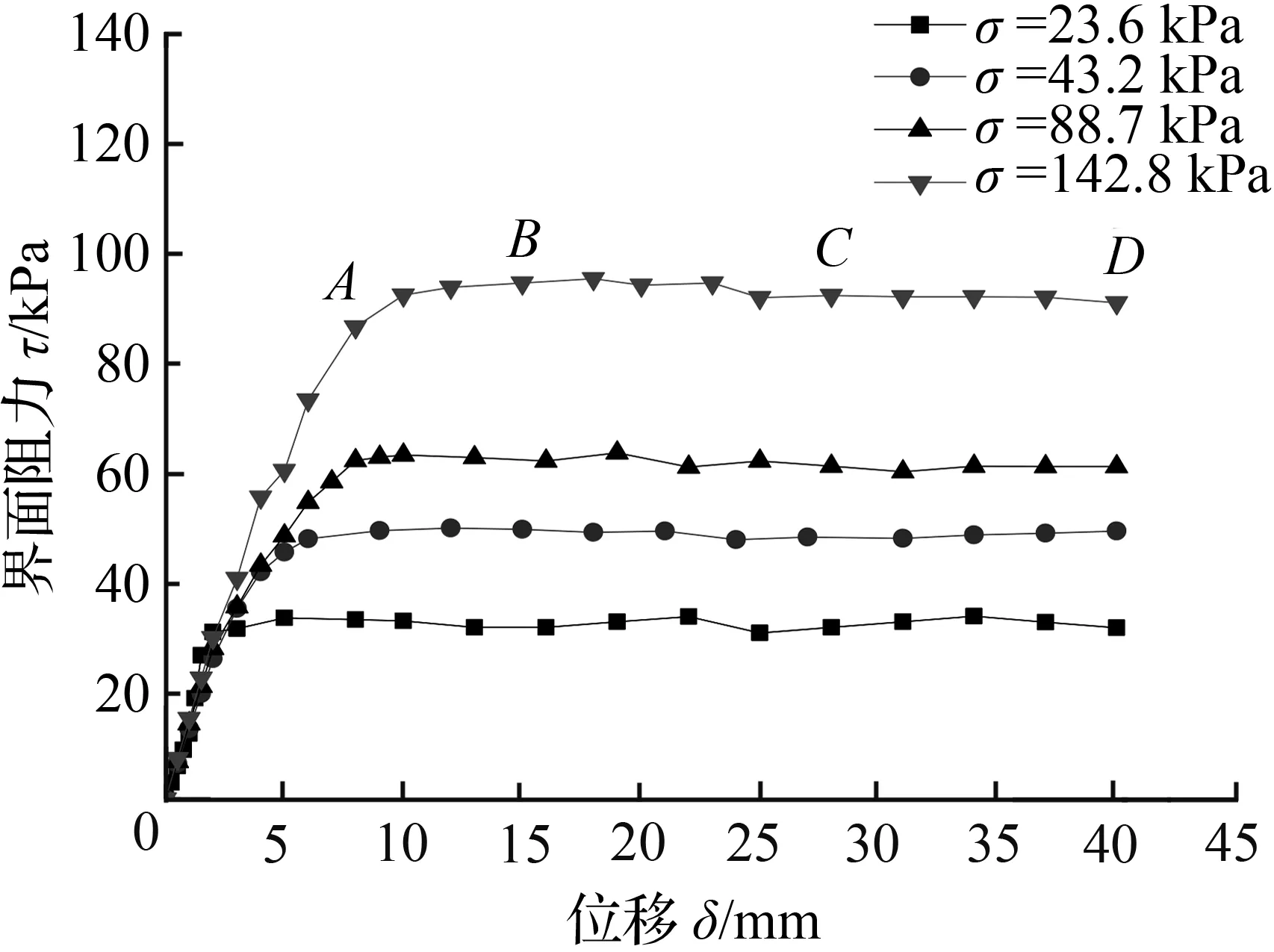
(d) Ⅳ粗糙度板

图5 相同粗糙度不同法向应力下剪切应力—剪切位移曲线
Fig.5 Stress-strain relationship under different normal stress

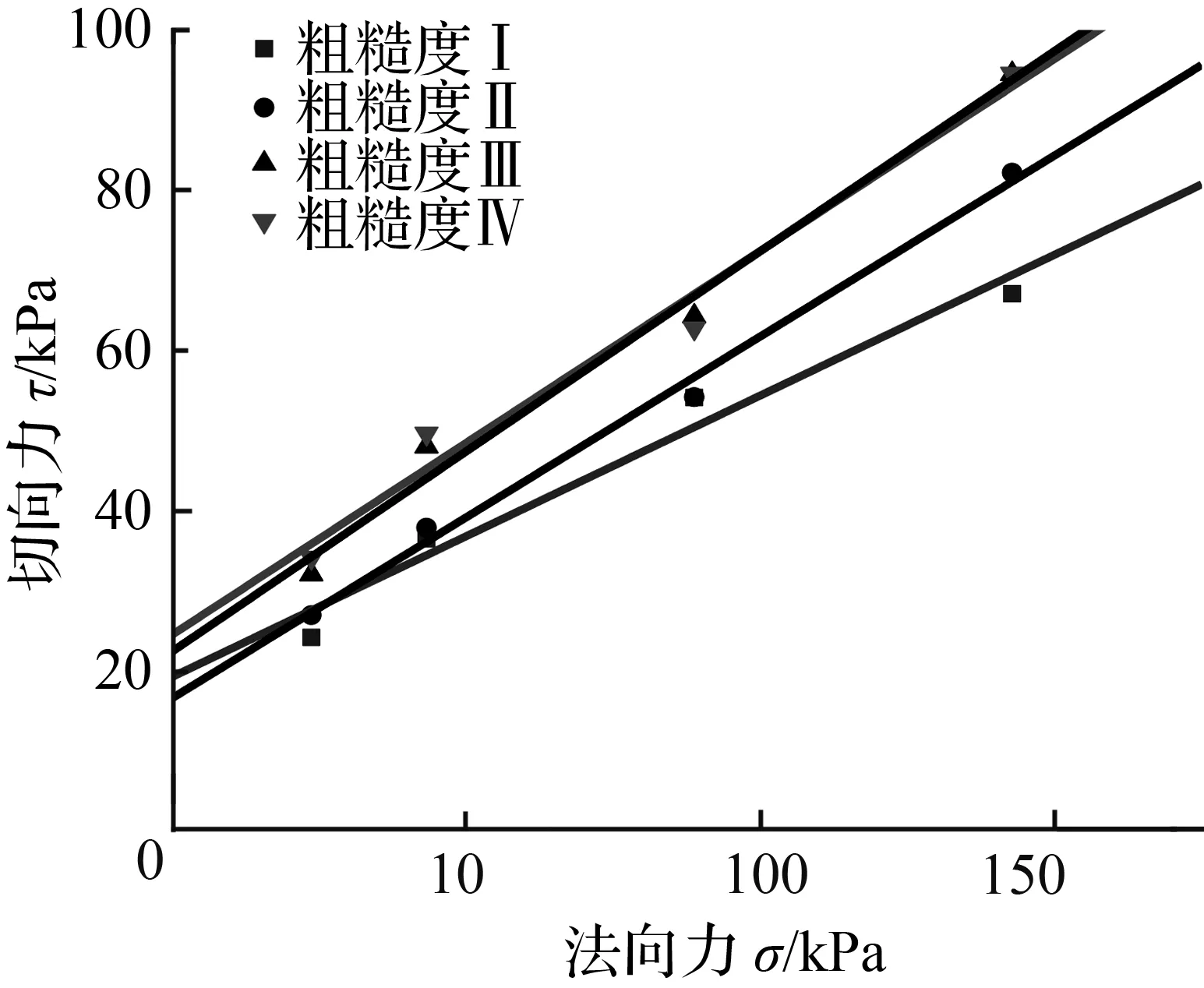
图6 不同粗糙度下抗剪强度线Fig.6 Line of shear strength under different roughness

根据黏着—犁沟摩擦理论，相同表面特性的黏性土—混凝土界面其单位面积上的犁沟力、黏着结点的剪切强度属于固定值，剪切范围内的微凸体的数量大致相同，即犁沟面积不变，而摩阻力产生变化应归因于法向力的增加造成黏着面积的变化。根据式(4)的变化可以认为，黏着面积与法向力成线性关系:

F↑=T↑+Pe→=Ar↑·τb→+S→·pe→。

(4)

需要指出的是，库仑强度理论认为剪切强度是由黏着力和内摩擦角产生的摩阻力共同提供，图6在法向力为0时不同混凝土齿板界面c值不同，其解释是因为土体黏聚力改变而引起切向力不同。而根据黏着—犁沟理论认为剪切强度由黏着力和犁沟力组成，法向力不变的情况下黏着力不改变，界面粗糙度的变化造成犁沟力改变，法向力为0时剪切力的变化是由于犁沟力变化而引起的。这说明法向力为0时，切向力并不是单纯的由土体黏聚力组成，而是黏着力与犁沟力共同组成。换言之，库仑强度理论的内聚力c的物理含义并不仅仅是由土体黏性造成的。

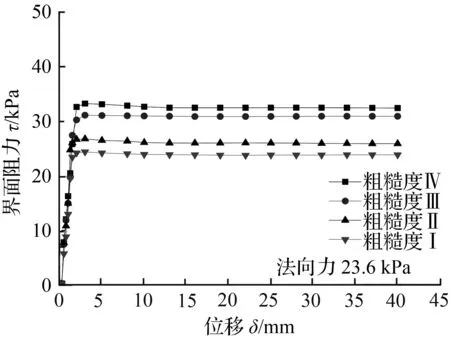
(a) 法向力23.6 kPa

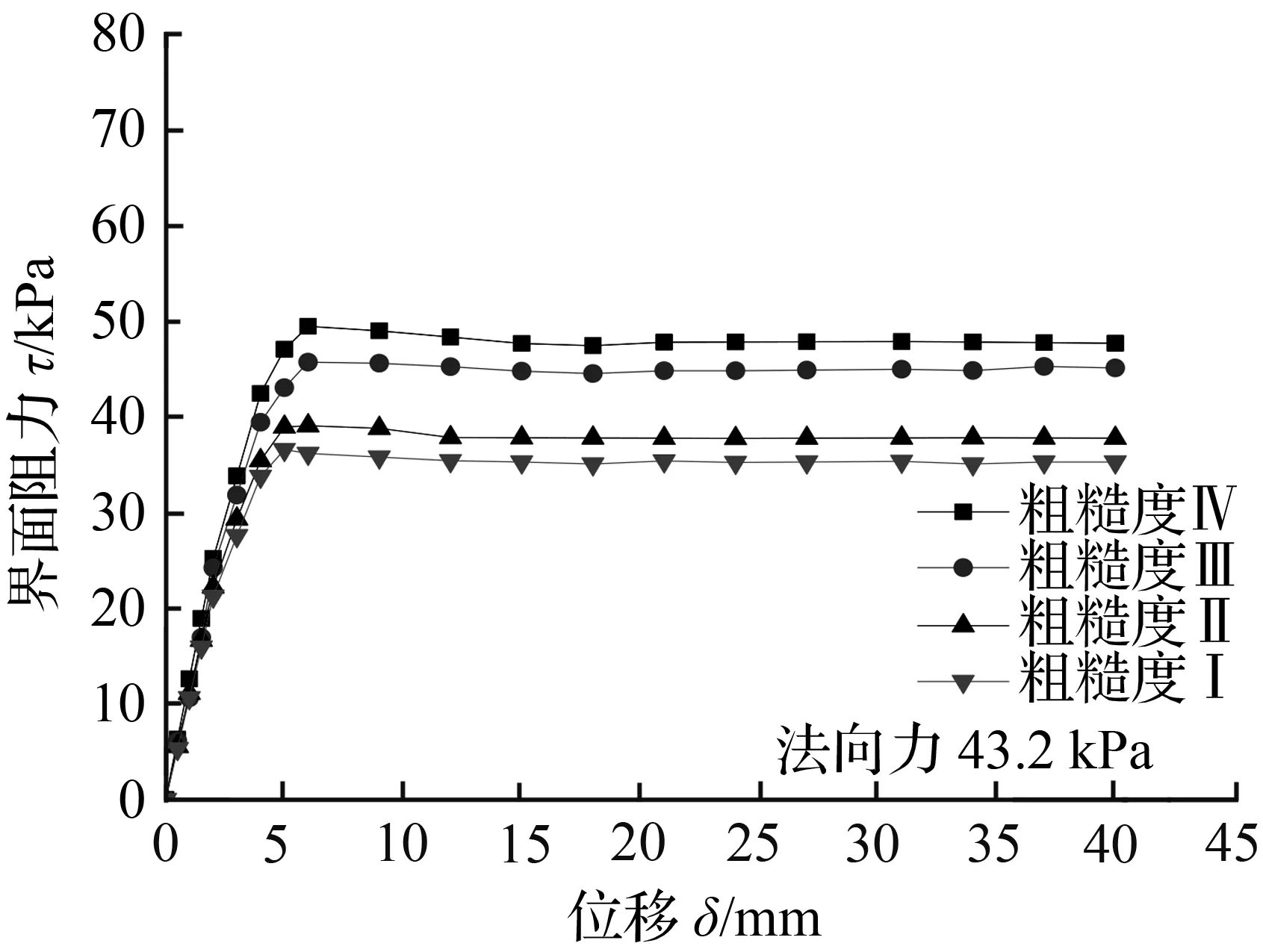
(b) 法向力43.2 kPa

(d) 法向力142.8 kPa

图7 相同法向力不同粗糙度下剪切应力—剪切位移曲线
Fig.7 Stress-strain relationship under the same normal force and different roughness

根据黏着—犁沟摩擦理论，相同表面特性的黏性土—混凝土界面其单位面积上的犁沟力、黏着结点的剪切强度属于固定值；在相同法向力作用下，黏着面积没有产生变化，混凝土齿形板外轮廓的变化直接改变了剪切面处微凸体的数量，即犁沟面积产生了变化，变化趋势如式(5)所示，印证了犁沟力是摩阻力的组成部分：

F↑=T→+Pe↑=Ar→·τb→+S↑·pe→。

(5)

从表2中可以看出，在相同法向力作用下，随着齿板峰谷距的增大，剪切力会相应增加，但最大剪切力均小于土体剪切强度。这是因为当黏性土—混凝土界面剪切强度大于黏性土体剪切强度时，剪切破坏将产生于土体内部而不发生在黏性土—混凝土界面，剪切力的最大值仅能达到土体剪切强度。与文献[16]结论类似。

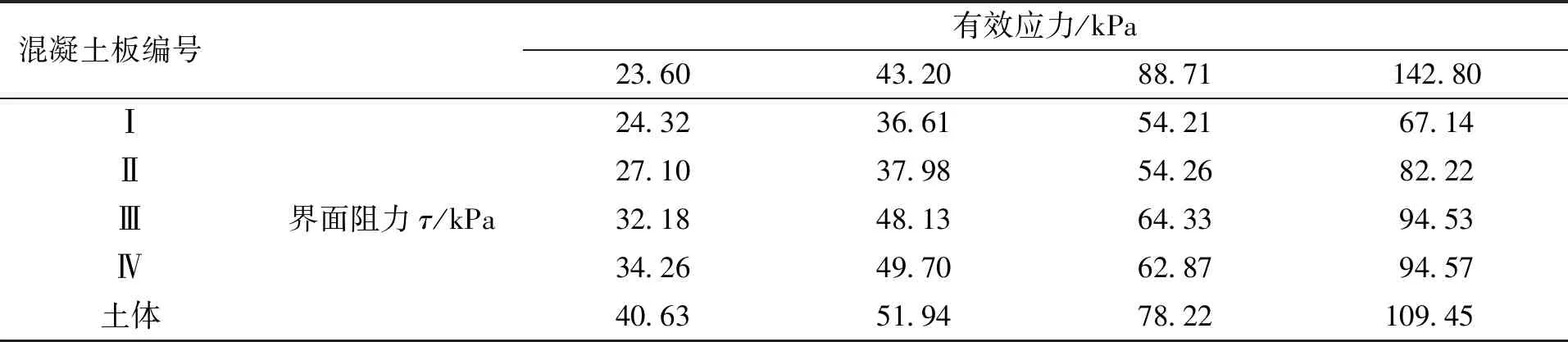
表2 黏性土—混凝土界面阻力Tab.2 Interface resistance between cohesive soil and concrete

2.2 黏性土—混凝土界面弹塑性

根据文献[14]反向剪切试验，界面发生正向剪切后(θ=0.5、0.75、1曲线)所得到的反向剪切力明显低于未剪切界面剪切力(θ=0曲线)，说明正向剪切后造成部分微凸点产生迁移无法在反向剪切时提供等量的剪切力。界面发生正向完全剪切破坏后的反向剪切力(θ=1.0曲线)由黏着力和弹性犁沟力及因正向剪切造成微凸体迁移而新形成的微凸体在反向剪切时所提供的犁沟力组成。

说明黏性土—混凝土界面剪切从初始阶段到破坏阶段均存在弹塑性变形，全阶段均为弹塑性共同作用的结果。

直剪试验得到的结果，如图6所示，界面粗糙度的变化造成犁沟力改变，法向力为0时初始剪切力的不同是由于犁沟力变化而引起的。这也印证了从初始阶段即存在弹塑性变形。

2.3 黏性土—混凝土界面受力综述

根据黏性土—混凝土直剪试验应力—位移曲线结合黏着—犁沟理论对其摩擦原理进行描述：试验准备阶段，放置混凝土块及黏性土后，在自重作用下两界面接触；当法向力作用后，黏性土及混凝土界面接触较自重作用下更加紧密，即是由于法向力增加后微凸体顶端相接触部分的应力达到受压屈服极限σs而产生塑形变形，土体微凸点达到受压屈服极限后，只能通过增加已有有效微凸体的接触面积或增加界面间有效接触微凸点的数量来增加承载法向力的受荷面积。此过程中犁沟接触点的数量并不因法向接触力的增大而增加。

剪切开始后，剪切力是由黏着力和犁沟力共同提供。由于法向力不发生变化，黏着力的大小即受荷面积不会发生变化，在切向力作用下黏结点被剪切产生滑动，需形成新的黏着点保证受荷面积不变，剪切过程中黏着面积的位置在不停地变化。

同样的，剪切开始后，随着剪切位移的逐步增大，犁沟点数量也在逐步增加，犁沟面积也在随之增大，剪切力上升并达到峰值。随着剪切的进一步发展，土体颗粒的迁移使混凝土表面的微凸体及土体表面的微凸体被逐渐填平或削平，剪切位移的增大无法形成更多的数量的犁沟点，犁沟面积也随之下降，剪切力下降，这一过程即是黏性土—混凝土剪切软化的过程，这一过程结束时对应的剪切位移既是残余强度开始位移。剪切位移继续扩大，塑性犁沟微凸点均已完成迁移，土体表面和混凝土表面基本被填平，微凸点的数量也因迁移而大大减少，这时残余强度由黏着力和弹性犁沟力构成，弹性犁沟点的数量并不因位移的增加而变化,基本保持稳定。

3 黏着—犁沟界面法向力、实际接触面积与颗粒之间的关系(微凸体与颗粒间的数学表达)

根据界面剪切试验得到的结果，相同表面特性的黏性土—混凝土界面法向力与黏着面积呈线性关系。若黏着面积可以用颗粒的面积表示，将建立起法向力与颗粒之间的关系。

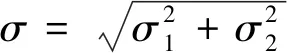
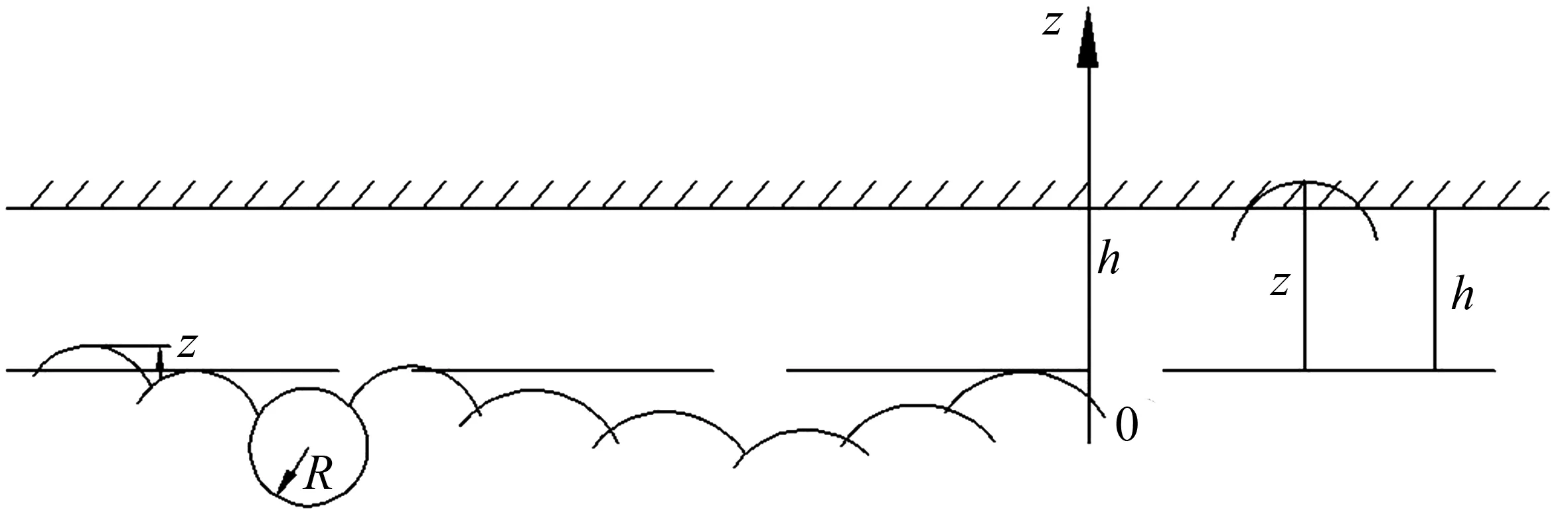
图9 Greenwood和Williamson的随机表面模型Fig.9 Greenwood and Williamson random surface model

只有当概率密度分布曲线中，微凸点高度z>h的部分发生黏着接触，即

(6)

如果粗糙表面微凸体总数量为n，则参与接触的微凸点数m为：

(7)

各个接触点的法向变形量为z-h，根据接触力学[18]求得单个微凸点的接触面积，再与参与接触的微凸点数m相乘，求得实际接触面积A为：

(8)

同样，根据微凸点法向荷载W为：

(9)

(10)

(11)

(12)

(13)

(14)

从式(13)、(14)可以看出法向力与实际接触面积、微凸体数量均呈线性关系，W/A或W/m的比值均与高度分布函数无关。理论的推导与试验得出同一结论，在一定情况下法向力与实际接触面积成正比。微凸体中的颗粒与法向力建立了联系，为颗粒级别的计算打下基础。

4 黏着—犁沟理论对桩土界面的应用

4.1 黏着—犁沟理论与库仑强度理论的区别

对于相同条件下的桩—土界面，库仑强度理论认为界面法向力的增减改变的是由内摩擦角产生的桩土界面摩擦力(σtanΦ)，界面间接触力的增减没有改变即黏聚力c。黏着—犁沟理论认为法向力的增减改变了黏着的实际接触面积，因而造成黏着力的变化；法向力的增减也改变了犁沟接触面积。所以说库仑强度理论中的黏聚力与黏着—犁沟理论中的黏着力并不等同。

对于直剪试验中的混凝土齿形板而言，其峰—谷距明显大于颗粒粒径，峰—谷距的变化对于混凝土表面平整度的性质没有改变，而是改变剪切面的黏着面积与犁沟面积来变化“传统意义上的粗糙度”(即库仑强度理论的Φ值)。

4.2 黏着—犁沟理论对桩土界面的实际应用

直剪试验所用的混凝土齿板Ⅰ可以代表大部分桩身表面，但黏性土的粗糙度变化较大无法用单一试验土样代表。库仑强度理论的内摩擦角、黏聚力等要素为宏观意义上的平均值，较难进一步解释细观问题；而黏性土—桩体界面剪切力应用黏着—犁沟摩擦理论中单位面积黏着力与实际黏着面积乘积、单位面积的犁沟力与犁沟面积乘积四要素表示，具有真实的物理意义，切向力的来源更为直观。黏着面积与法向力呈线性关系，犁沟面积与微凸体的分布有关，单位面积上的黏着力与单位面积上的犁沟力又与材料本身的性质有关。在不改变土体性质的前提下，黏性土—桩接触问题的细观实质是黏着颗粒的数量与犁沟颗粒数量的变化，这就将在颗粒级别的真实物理量与宏观的切向力之间搭建了桥梁。

4.3 黏着—犁沟理论存在不足

黏着—犁沟理论所提出的摩阻力是由黏着力和犁沟力两部分组成。桩土界面在实际应用中有水的存在，这将导致黏着结点的剪切强度变化，含水率与黏着结点的剪切强度之间的关系仍需进一步探究。桩土界面细观颗粒的分布直接影响实际接触面积，这将造成黏着点及犁沟点数量、黏着及犁沟面积、最大摩阻力、最大摩阻力位移等参数的变化，能够准确描述桩土界面颗粒分布函数仍然需要进行大量的研究。