削弱永磁直线电机法向力波动优化设计
2022-09-29王天鸿崔皆凡
王天鸿, 崔皆凡
(沈阳工业大学 电气工程学院,辽宁 沈阳 110000)
0 引 言
永磁直线电机(PMLM)的进给系统定位精度高、响应快、效率高且无行程限制,因此在高速进给系统的领域占据了主导地位。直线电机存在初级铁心断开、开齿槽等特殊结构,会导致齿槽效应和端部效应[1-2]。在PMLM运行过程中,动子与定子之间会产生法向力波动,其数值很大,工作台会因此振动,同时法向力波动过大还会引起摩擦摄动、推力波动,影响加工精度,国内外学者对此进行了广泛的研究。针对齿槽法向力,文献[3]通过计算动子最佳齿顶宽度削弱齿槽法向力波动。文献[4]采用在永磁体表面粘贴薄铜片削弱气隙磁场高次谐波,从而抑制齿槽法向力波动。文献[5]通过磁极偏移使永磁体产生的磁场相互抵消,消除谐波,削弱齿槽法向力波动,但其计算过程相对复杂,每一个磁极的偏移距离均需要单独计算,并且在一定程度上受到空间限制。文献[6]通过在动子上开辅助槽抑制齿槽法向力波动,但其应用范围窄,只适用于整数槽电机,分数槽电机开辅助槽反而会使法向力波动增大。针对端部法向力,文献[7]通过端齿倒角的方法抑制端部效应。文献[8]分析了阶梯状分布的端部辅助齿结构对端部效应的影响。文献[9]通过增加辅助极来减小法向力波动,取得了较好的效果。文献[10]将端部设计成V型结构。但这些方法均增加了电机结构的复杂性。除结构优化外,文献[11]通过使用电流补偿,有效抑制了端部法向力波动。
本文采用最优极弧系数和磁极倒角法削弱齿槽法向力波动,优化铁心长度及端齿形状削弱端部法向力波动,并通过有限元仿真分析电机整体的法向力波动,验证所提方法的有效性。
1 最优极弧系数削弱法向力
1.1 PMLM法向力分析
为了简化分析,作出以下假设[12]:
(1) 电枢铁心磁导率μFe为无穷大;
(2) 永磁体的磁导率与空气相同;
(3) 永磁体的磁力线是垂直进入动子铁心的,即只有法向磁场,而无切向磁场;
(4) 动子为无限长,即不考虑端部效应。
根据磁路基尔霍夫第二定律,永磁体产生的气隙磁场为
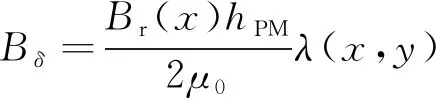
(1)
式中:Br(x)为永磁体的剩余磁感应强度;hPM为永磁体的磁化长度;μ0为真空磁导率;x为动子和定子之间的相对位置;y为电机某一点到原点的位置。
气隙比磁导为
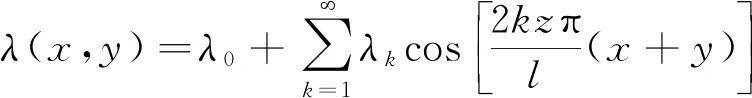
(2)
式中:λ0为气隙比磁导的不变部分;λk为气隙比磁导周期分量的幅值;z为电机槽数;l为铁心长度;k为谐波次数,k=1,2,3,…。
且有λ0、λk分别为
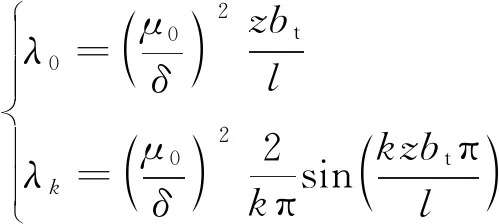
(3)
式中:δ为气隙长度;bt为齿宽。
永磁体剩余磁感应强度波Br(x)的傅里叶级数展开式为
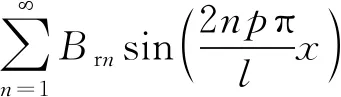
(4)
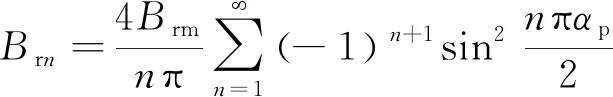
(5)
式中:p为极对数;αp为极弧系数;Brm为永磁体剩余磁感应强度最大值。
由麦克斯韦张力张量定理得,动子铁心单位面积法向力:
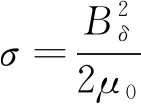
(6)
则PMLM动子法向力为
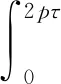
(7)
式中:lFe为铁心有效长度;τ为极距。
将式(1)、式(2)、式(4)、式(6)代入式(7)得PMLM动子法向力为
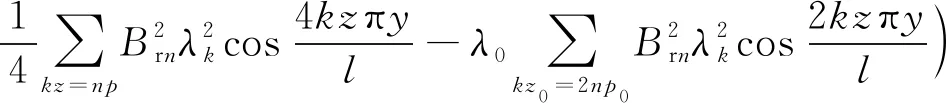
(8)
对Br(x)进行傅里叶分解之后,结合式(8)可以看出,对法向力波动产生作用的只有kz=np和kz=2np次傅里叶分解系数。
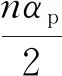
12槽11极PMLM,其极弧系数理论上选择3/4、5/6或2/3时,齿槽法向力波动最小。
1.2 PMLM推力分析
直线电机齿槽力的产生与旋转电机齿槽转矩原理相同,因此可通过旋转电机求出直线电机的齿槽推力。旋转电机齿槽转矩为
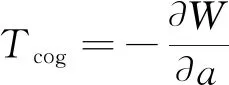
(9)
式中:W为电机磁场能量;a为位置角,即永磁体中心线与齿槽中心线的夹角。
电机磁场能量W为
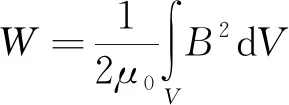
(10)
式中:B为气隙磁场强度;V为气隙体积。
忽略永磁体磁场储能变化,则:
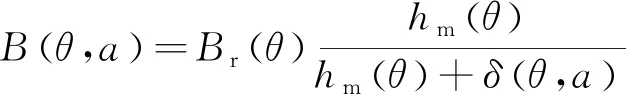
(11)
式中:B(θ,a)旋转永磁电机气隙磁密沿电枢表面的分布;Br(θ)为永磁体剩磁;δ(θ,a)为有效气隙长度;hm(θ)为充磁方向沿圆周的分布。
对Br(θ)进行傅里叶展开:
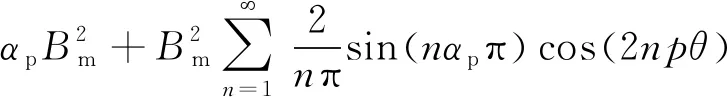
(12)
式中:Bm为永磁体剩磁密度。

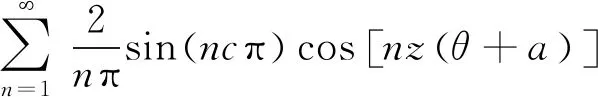
(13)
式中:c=bt/(bt+b0);b0为槽宽。
将式(12)和式(13)代入式(10),并进行简化得:
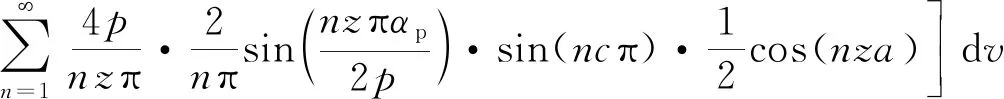
(14)
式中:n为使kz/np为整数的整数。
将PMLM动、定子间相对位移用x表示,则:
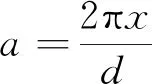
(15)
则PMLM齿槽力为

(16)
将式(14)和式(15)代入式(16)得:
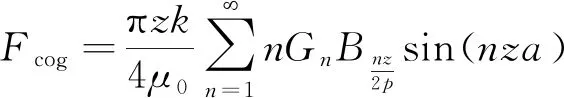
(17)
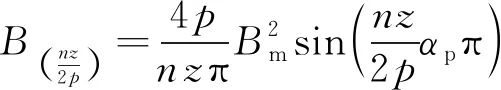
(18)
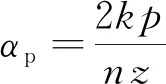
(19)
本文采用的是12槽11极直线电机,n=11的倍数。当n=55,k=48时,极弧系数为0.8;当n=11,k=5时,极弧系数为5/6。
1.3 有限元仿真分析
原始电机参数如表1所示。
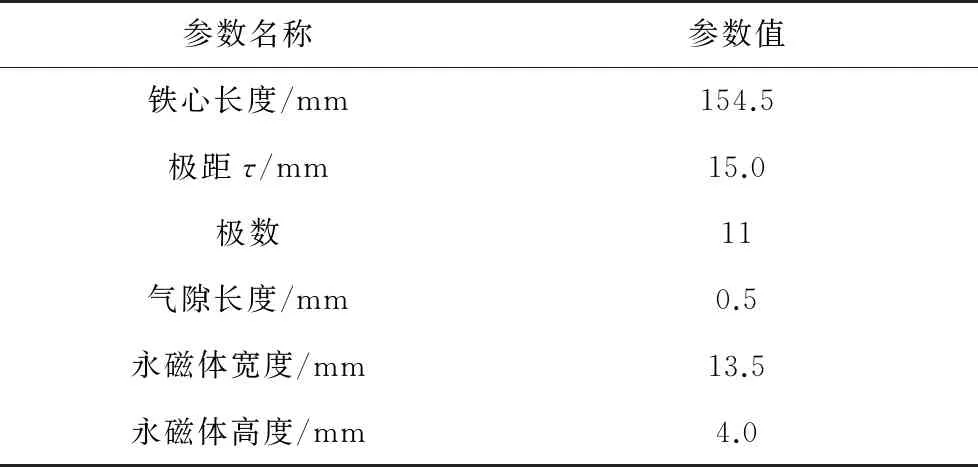
表1 电机参数
取不同极弧系数,法向力波动值、推力波动值及推力均值随极弧系数的变化如图1和图2所示。电机的法向力、推力波形如图3和图4所示。
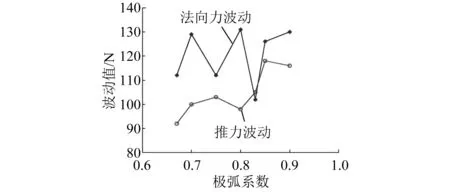
图1 波动值随极弧系数的变化曲线
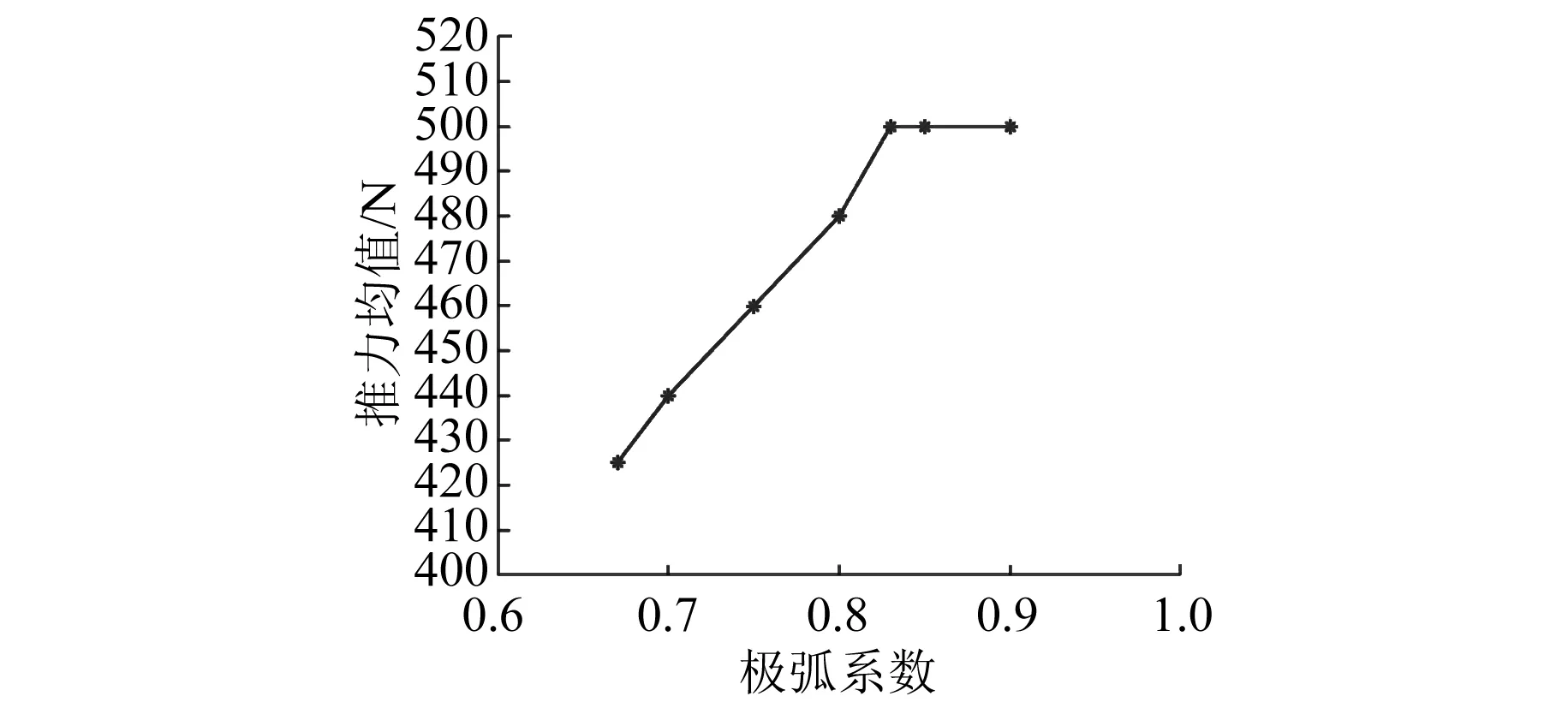
图2 推力均值随极弧系数的变化曲线
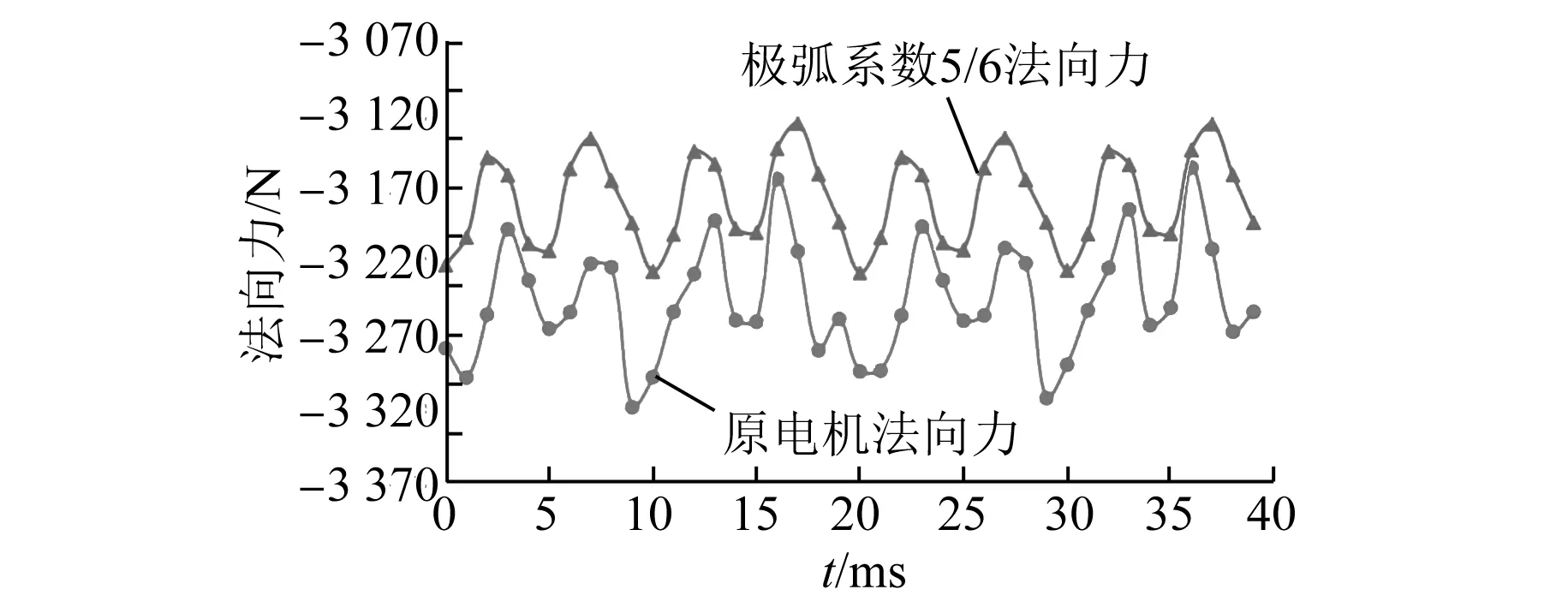
图3 电机法向力波形
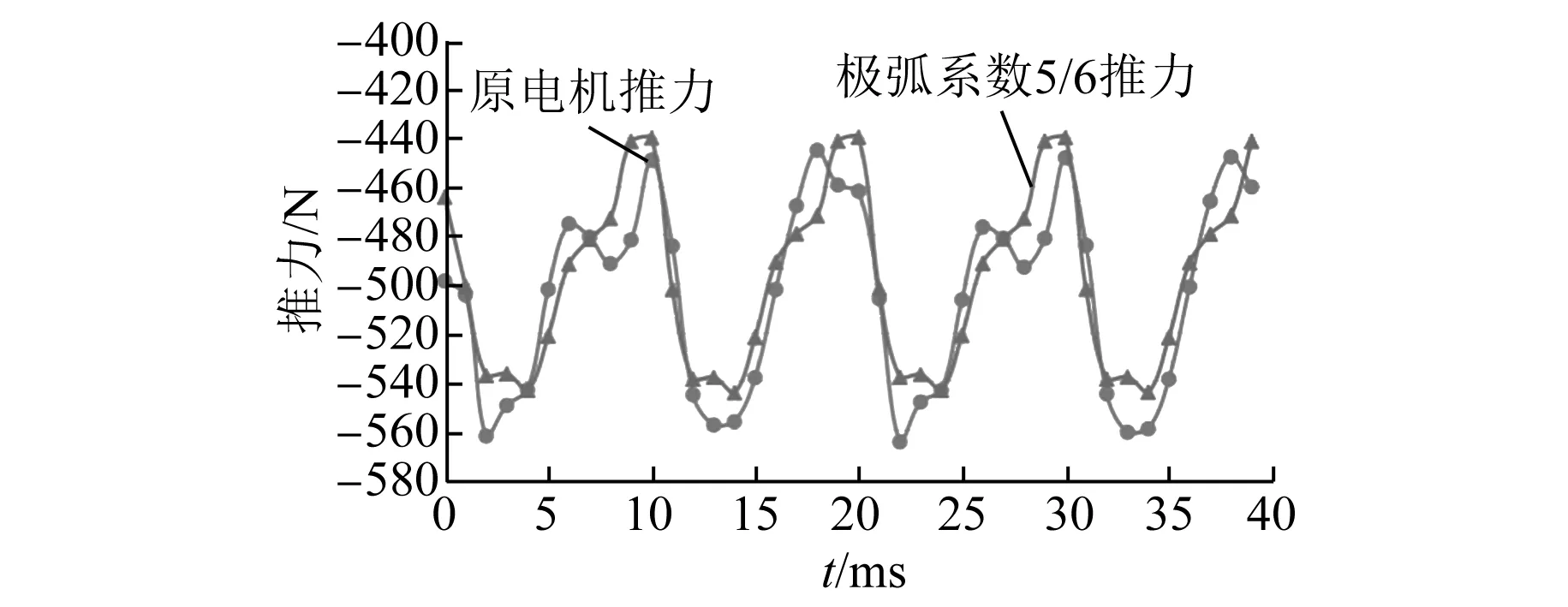
图4 电机推力波形
原电机最大法向力波动为130 N、最大推力波动为116 N,推力均值为500 N。由仿真结果可知,当极弧系数为5/6时,法向力波动最小,其最大法向力波动为102 N,比原电机降低了21.53%。
当极弧系数为0.8或5/6时,推力波动小,符合理论推导的结果。考虑推力均值及法向力波动的大小,选择极弧系数为5/6,最大推力波动降低为105 N,比原电机降低了9.48%;推力均值未改变。
2 磁极倒角削弱法向力
忽略铁心的磁阻及其饱和,PMLM的气隙磁密为
b(x,t)=f(x,t)λ(x,t)
(20)
式中:f(x,t)为永磁体磁动势;λ(x,t)为气隙比磁导。
永磁体磁动势中μ次谐波表达式为
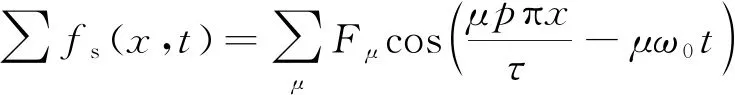
(21)
式中:ω0为基波角频率;Fμ为永磁体磁动势μ次谐波幅值。
气隙比磁导表示为
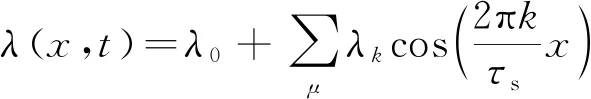
(22)
式中:τs为槽距。
则气隙磁密为
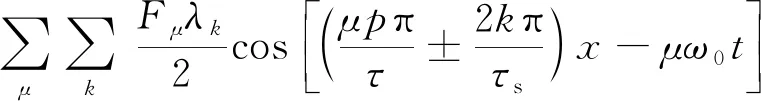
(23)
由麦克斯韦张力张量定理得,动子铁心单位面积法向力:
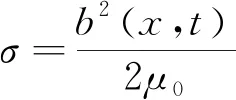
(24)
则法向力密度表达式为
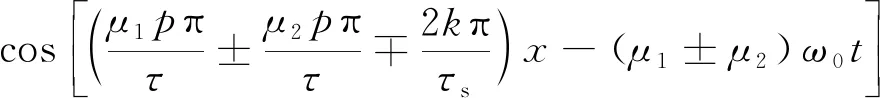
(25)
式中:μ1为气隙磁密谐波次数;Fμ1为气隙磁密μ1次谐波幅值;μ2为齿谐波次数;Fμ2为μ2次齿谐波幅值。
式(25)中第3项由气隙磁密与齿谐波相互作用产生,对法向力波动的影响最大,永磁体产生趋于正弦的气隙磁密时,产生的法向力波动最小,因此采用永磁体倒角改善永磁体磁密。同时,气隙磁密趋于正弦时,还会减小齿槽推力的波动。
一般磁极倒角有两种方法,即倒圆角和倒尖角两种,如图5所示。
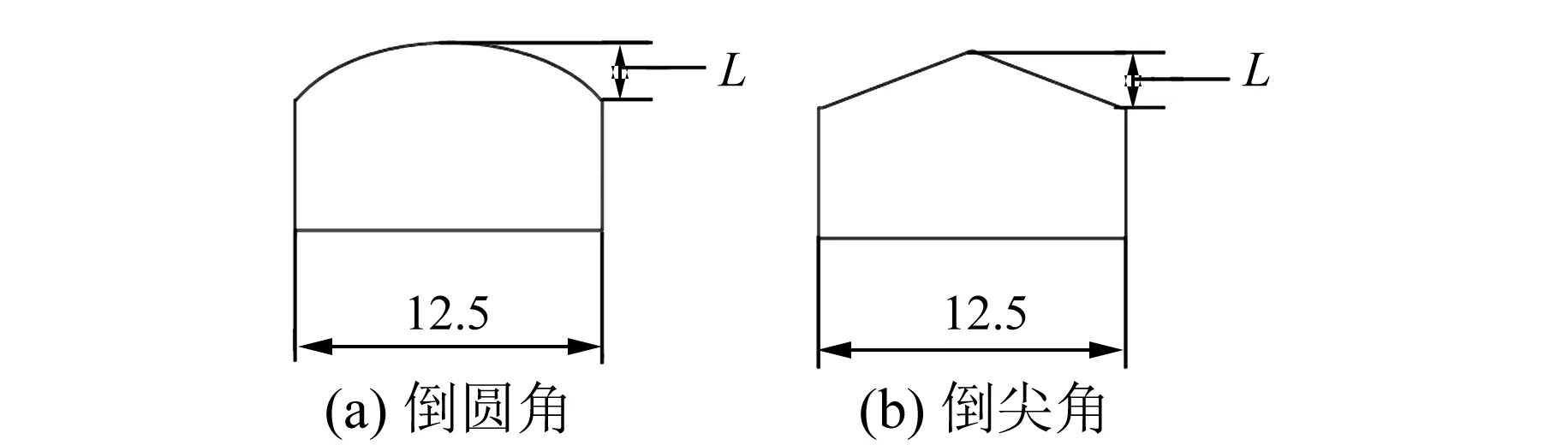
图5 磁极倒角方式
考虑加工难度等因素,本文选用倒尖角的方式,电机模型如图6所示。通过有限元仿真,原电机气隙磁密如图7所示;磁极倒角气隙磁密如图8所示;法向力、推力波动值和推力均值随倒角高度L的变化如图9和图10所示;电机的法向力和推力波形如图11和图12所示。

图6 磁极倒角电机模型

图7 原电机气隙磁密
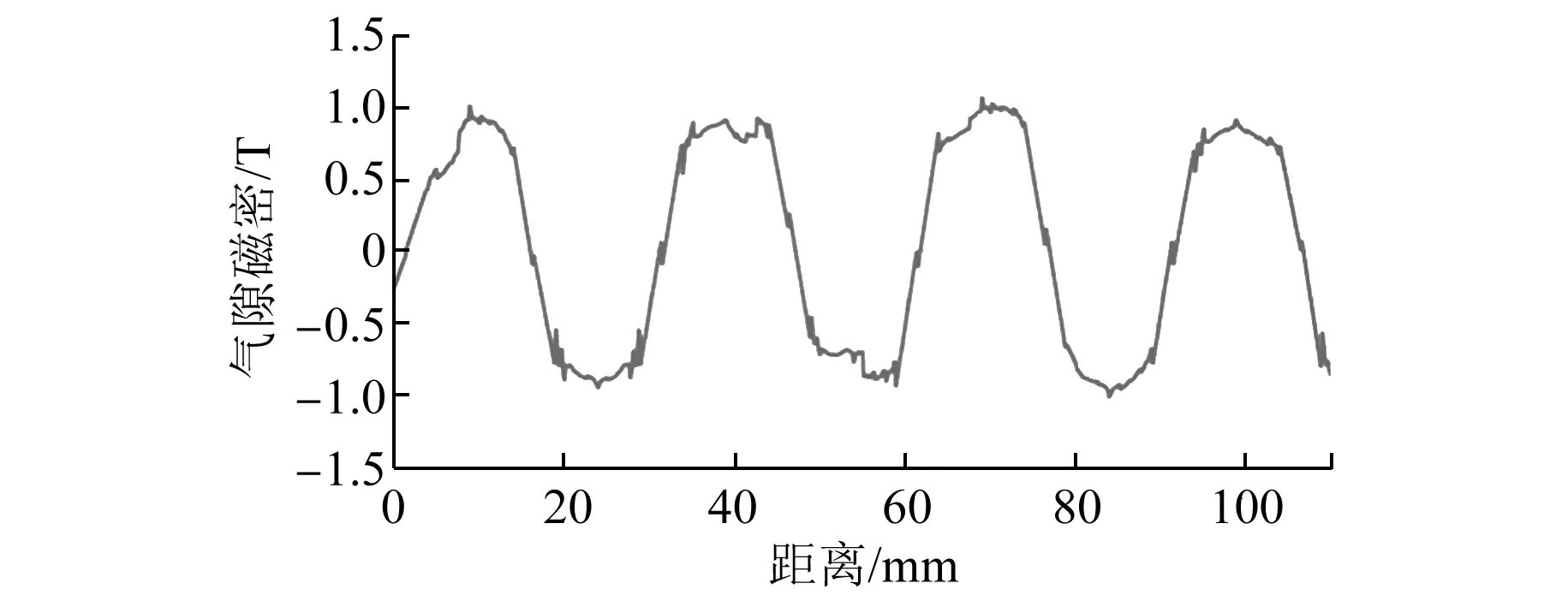
图8 磁极倒角气隙磁密
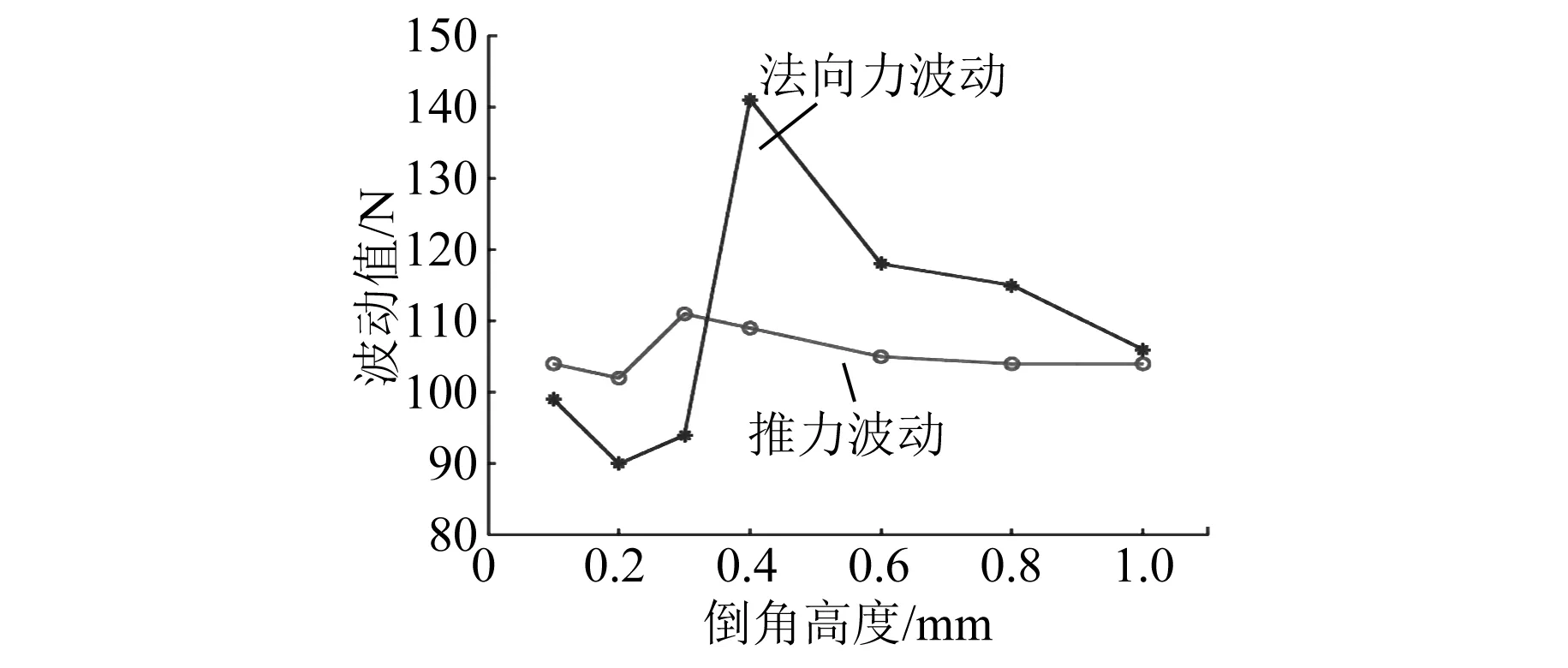
图9 波动值随倒角高度的变化曲线
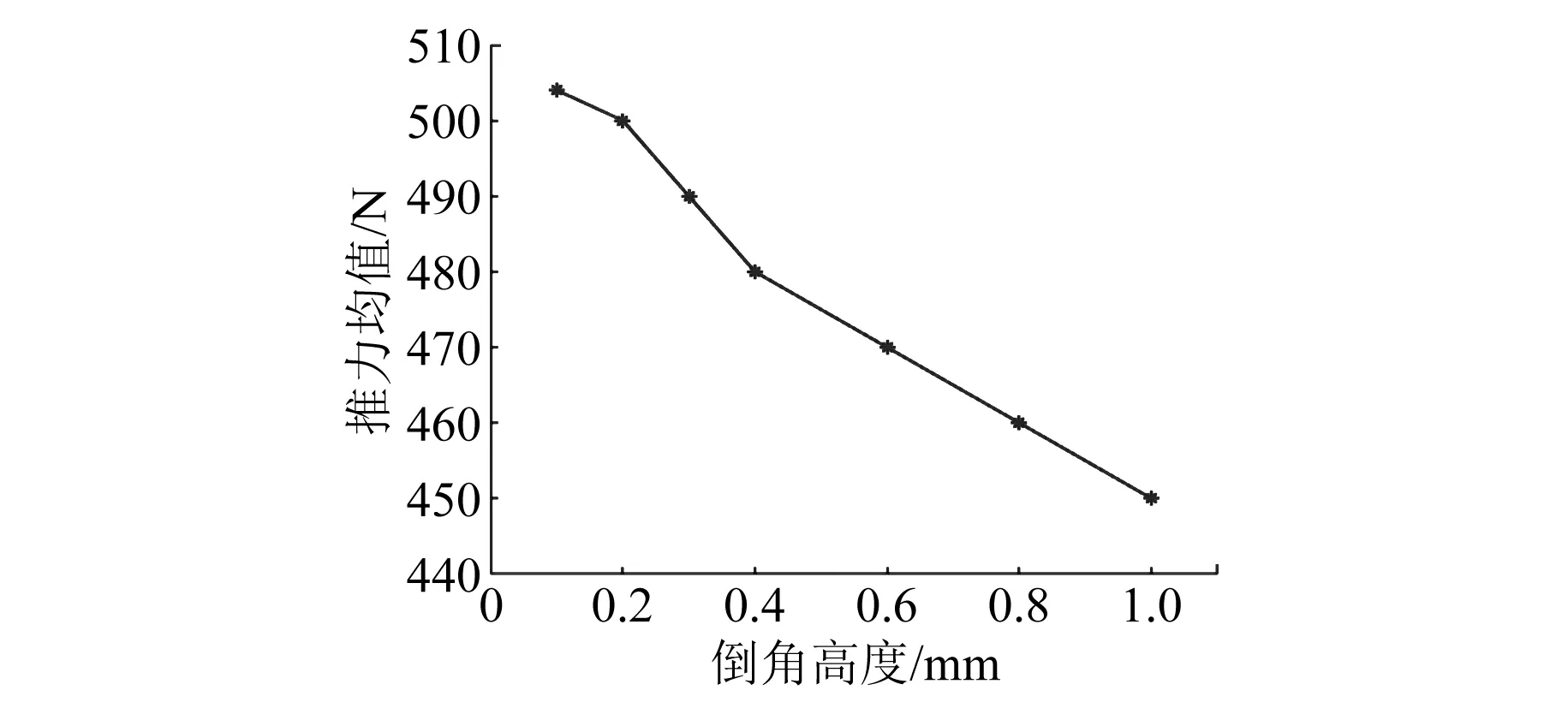
图10 推力均值随倒角高度的变化曲线
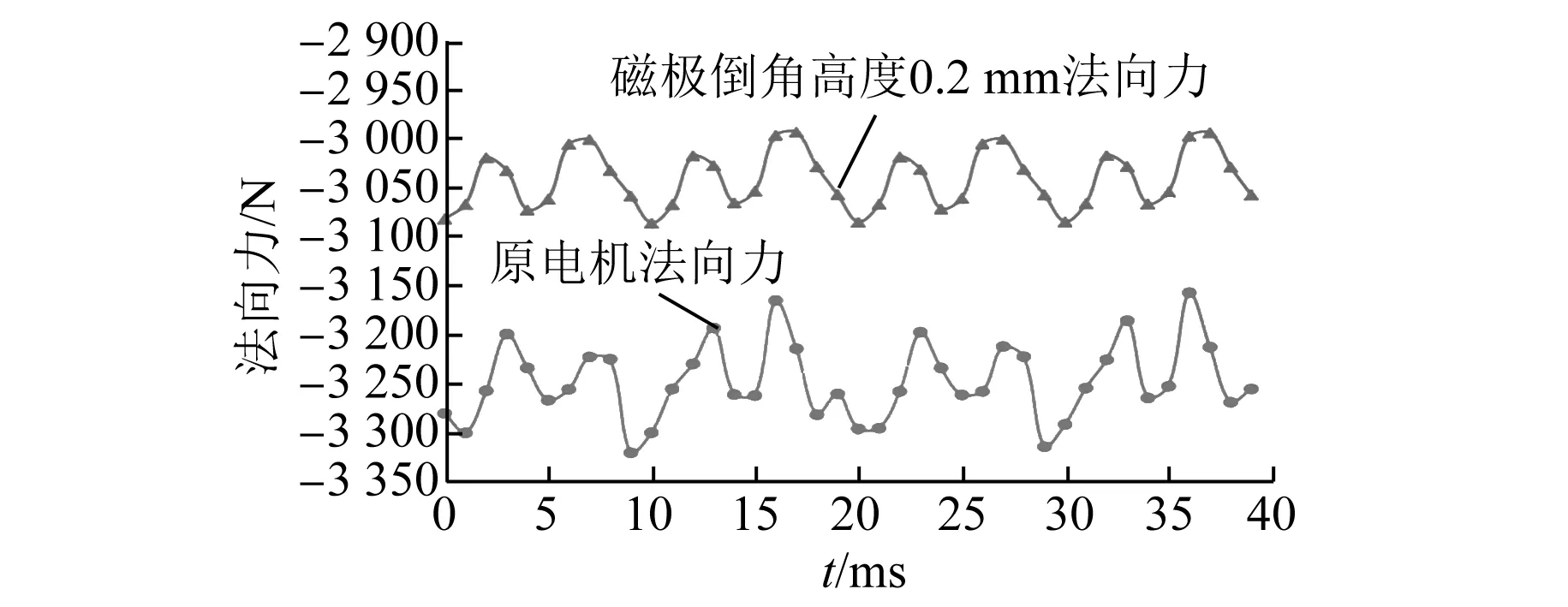
图11 电机法向力波形
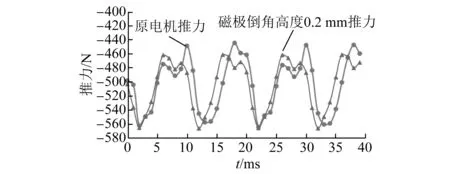
图12 电机推力波形
由图7和图8可知,经过磁极倒角后气隙磁密更加趋近于正弦。由图8~图12可知,当倒角高度L为0.2 mm时,削弱法向力波动的效果最佳,其最大法向力波动为90 N,比原电机降低了30.76%;最大推力波动降低为102 N,比原电机降低了12.07%;推力均值未改变,验证了理论的正确性。
3 优化铁心长度削弱法向力
3.1 直线电机法向力分析
动子铁心移动时,穿过法向端面的磁通傅里叶展开为
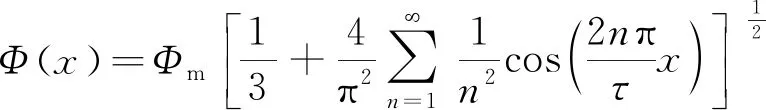
(26)
式中:Φm为经过动子铁心边缘磁通量最大值。
空间中单位体积的磁场能量为
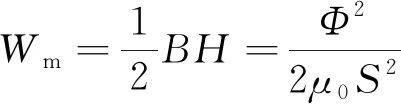
(27)
式中:Φ为经过动子铁心纵向边缘的磁通;S为磁感线在铁心纵向表面所围面积。
当动子铁心经过一个极距长度τ时,气隙磁场储能发生了变化,储能变化量为Wm:
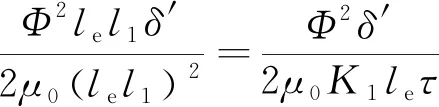
(28)
式中:le为动子铁心叠压厚度;δ′为气隙长度;V为气隙体积;l1为经过铁心纵向边缘又返回永磁体的这部分磁感线在永磁体横向所占的长度,l1=K1τ;K1为磁通压缩系数。
将式(26)代入式(28)得:
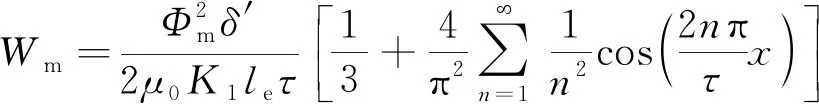
(29)
则沿着动子铁心运动的方向,动子铁心前端和后端所受端部法向力可表示为
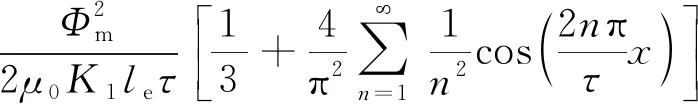
(30)
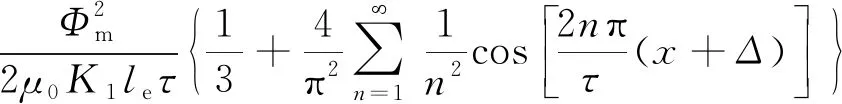
(31)
由式(30)和式(31)可以看出,PMLM端部法向力波动前后两端均以极距τ为周期,只有初相位不同。削弱端部法向力波动,只需使Δ=τ/2,则前后两端的法向力大小相等、方向相反,可在最大程度上相互抵消。
3.2 PMLM推力分析
当动子铁心长度超过3倍极距以上时,铁心两端所受的端部力相互独立,因此,电机推力等于两端端部力的合力。
F+为动子铁心前端端部力,F-为动子铁心后端端部力,则:
F+=-F-(-x-δ)
(32)
式中:δ=kτ-LFe,LFe为动子铁心长度。
将前后两端端部力傅里叶级数展开得:
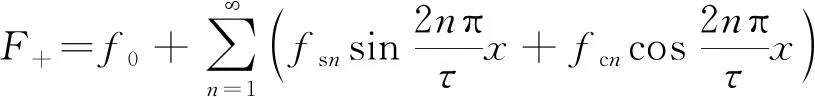
(33)
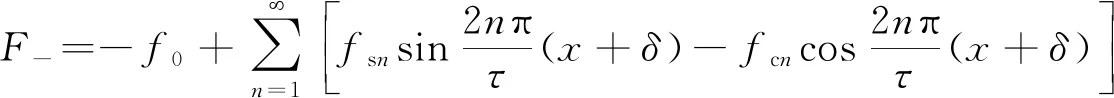
(34)
则推力为
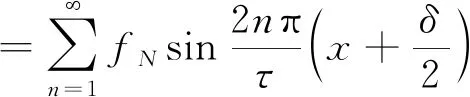
(35)
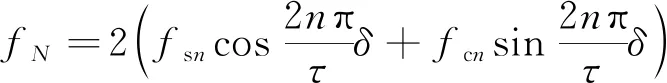
(36)
式中:fsn和fcn为傅里叶展开次的正弦、余弦系数;fN为振幅系数。
由式(35)可知,当LFe=kτ±π/2时,PMLM推力波动最小。
综合分析可知,当LFe=kτ±π/2时,PMLM推力波动及法向力波动均最小。
3.3 有限元仿真分析
法向力、推力波动值和推力均值随铁心长度的变化如图13和图14所示。电机的法向力和推力波形如图15和图16所示。
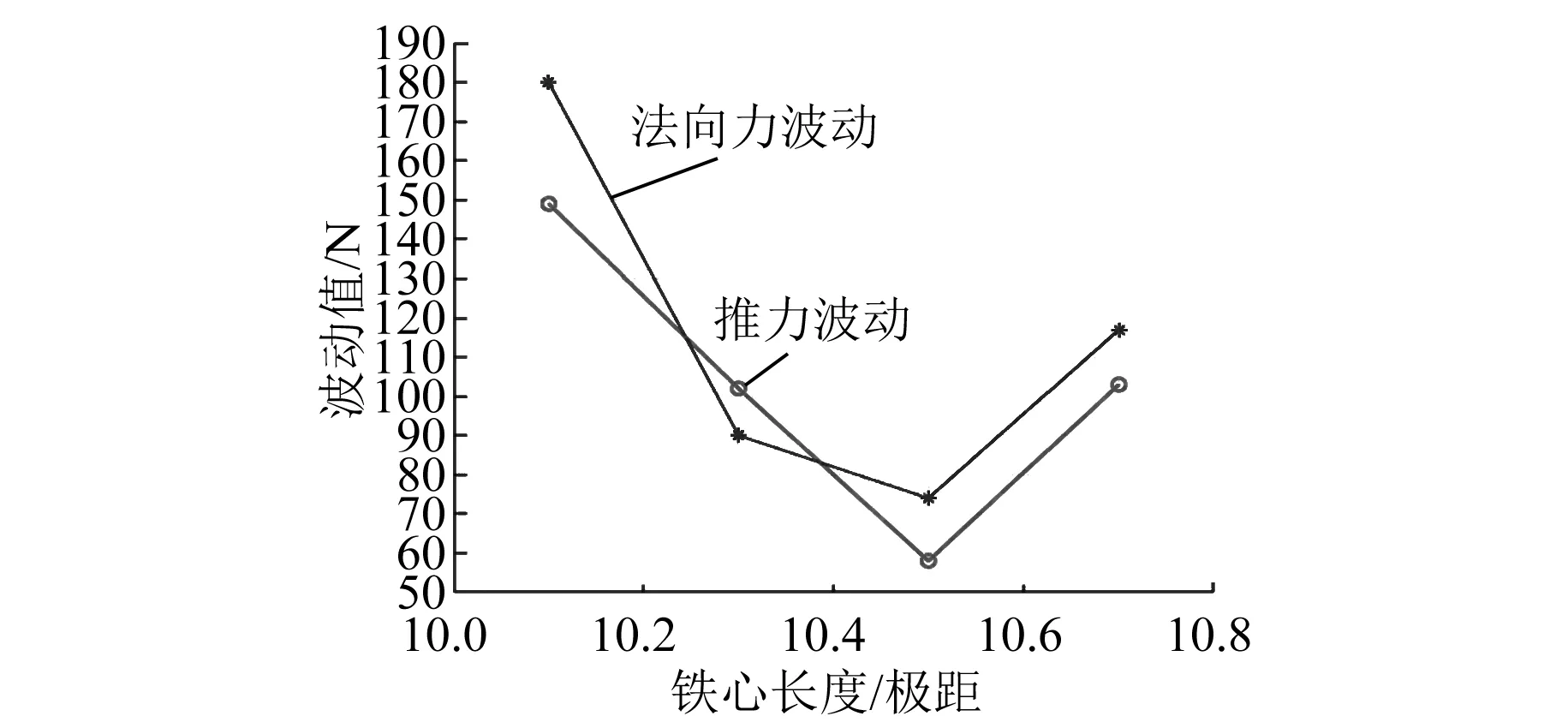
图13 波动值随铁心长度/极距的变化曲线
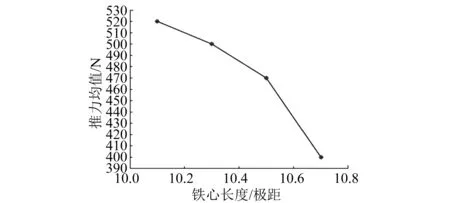
图14 推力均值随铁心长度/极距的变化曲线
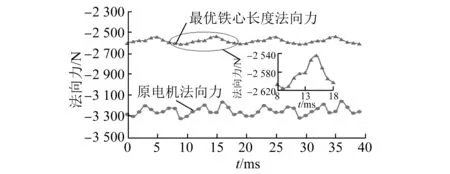
图15 电机法向力波形
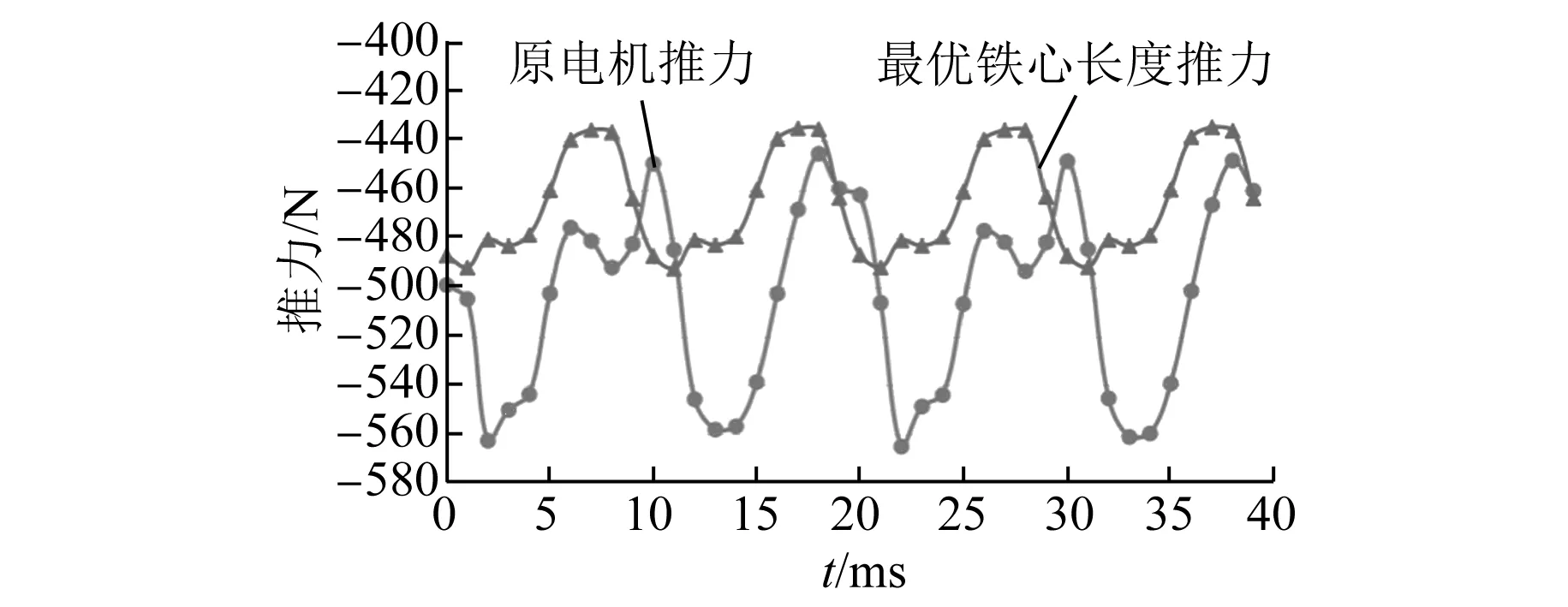
图16 电机推力波形
由仿真结果可知,铁心两端相差0.5倍极距时,法向力波动最小,其最大法向力波动为74 N,比原电机降低了43.07%;最大推力波动降低为58 N,比原电机降低了50%;推力均值略有降低,降低了6%。
4 优化端齿形状削弱法向力
PMLM动子铁心两端开断,端部气隙磁阻突变,产生端部法向力波动。优化端齿形状可以有效抑制端部法向力波动[14]。端齿形状有如图17所示的4种拓扑结构。
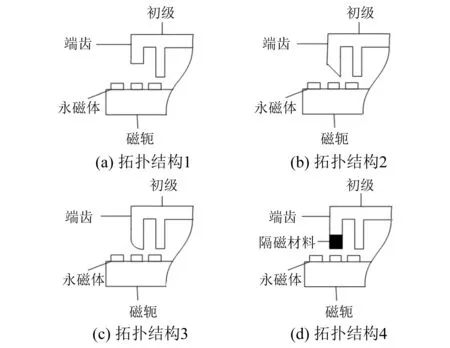
图17 4种常用的端齿拓扑结构
PMLM端部磁场十分复杂,建立精确的数学模型是十分困难的。图17中改变端齿的拓扑结构,其原理均为改变端部的气隙磁阻。
考虑实际加工难度,选择拓扑结构1对端齿进行优化,电机模型如图18所示。通过有限元仿真可得,原电机的端部气隙磁密和优化端齿的端部气隙磁密如图19和图20所示。波动值随端齿气隙的变化如图21所示。电机的法向力和推力波形如图22和图23所示。

图18 端齿优化电机模型
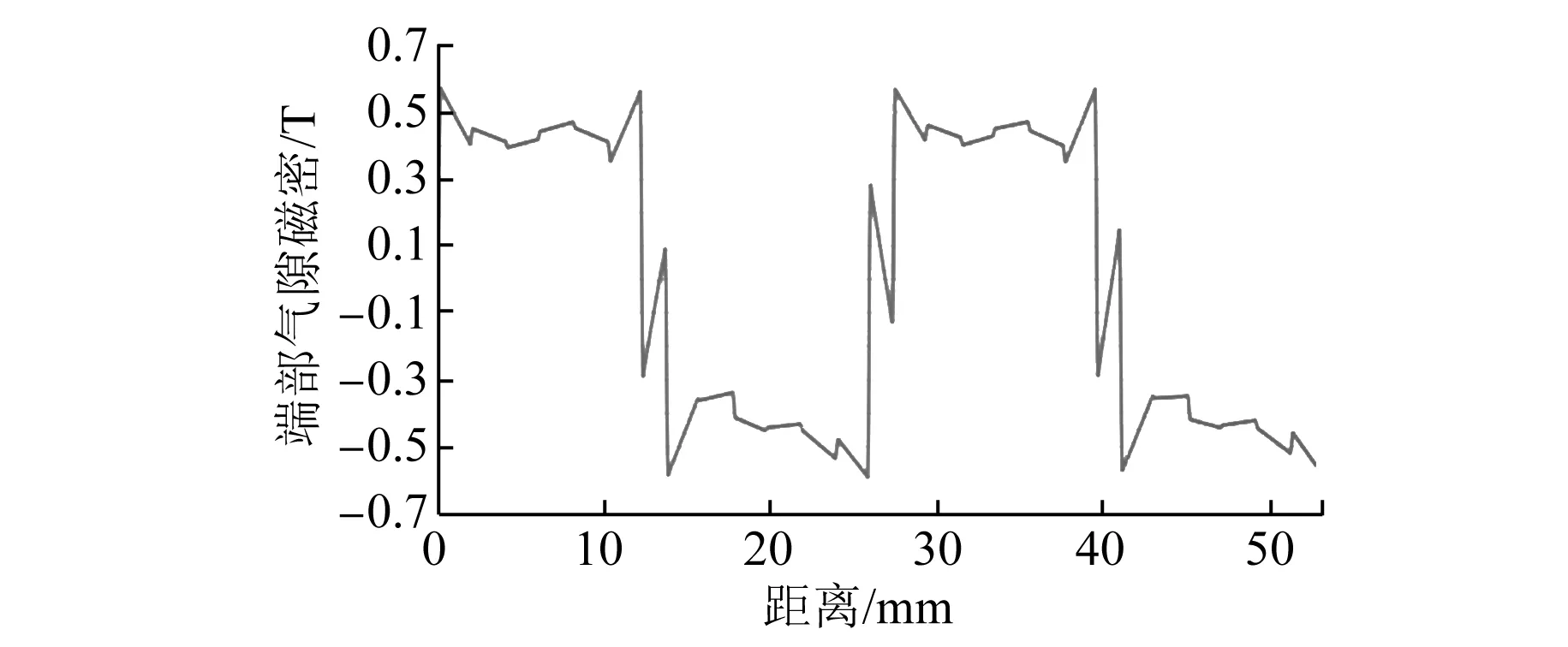
图19 原电机端部气隙磁密
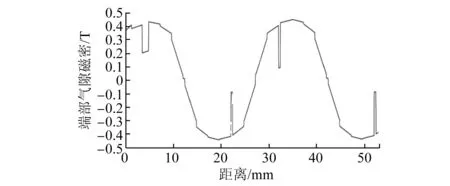
图20 端齿优化的端部气隙磁密
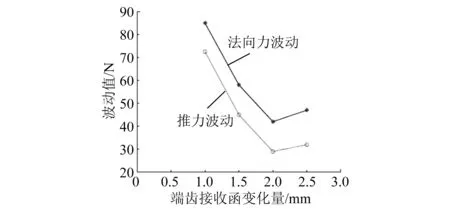
图21 波动值随端齿气隙的变化曲线

图22 电机法向力波形
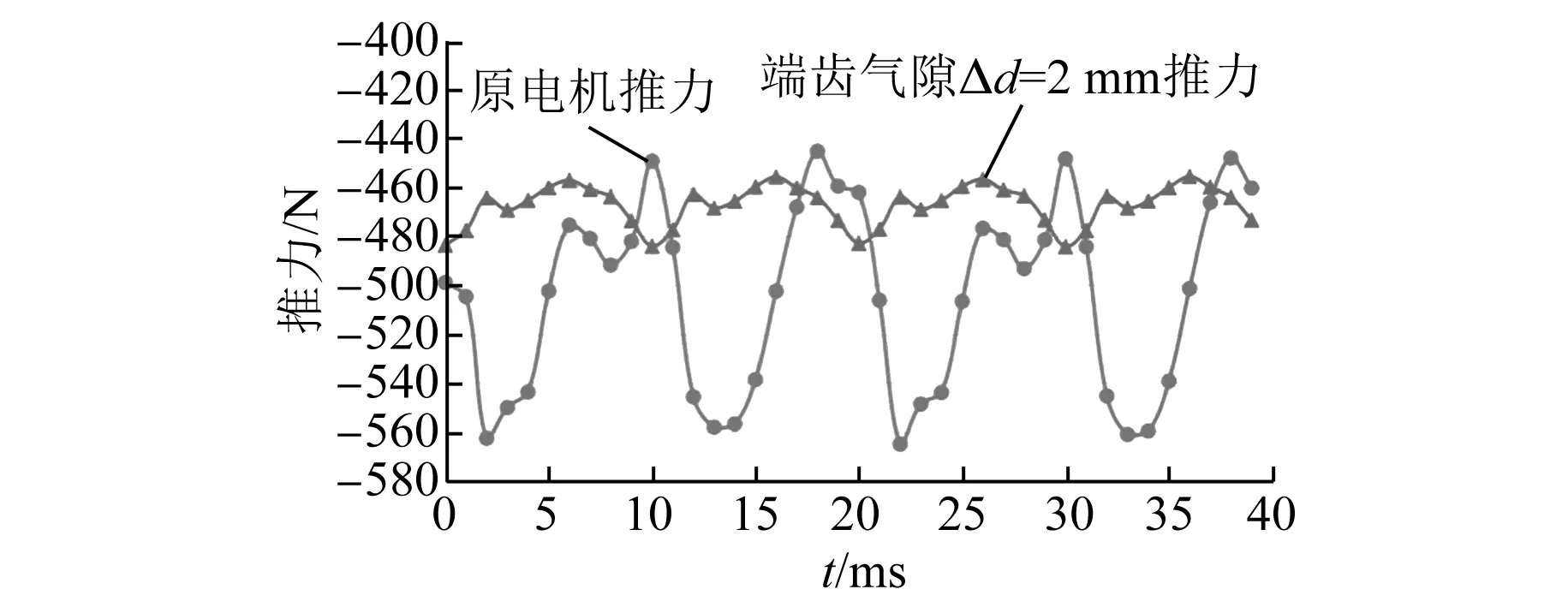
图23 电机推力波形
由图19和图20可知,改变端齿气隙可以优化端部气隙磁密,减小由端部效应造成的气隙磁密畸变。由图21~图23可知,当端齿气隙Δd=2 mm时,削弱法向力波动的效果最佳,其最大法向力波动为42 N,比原电机降低了67.69%;最推力波动降低为29 N,比原电机降低了75%;推力均值为470 N,略有降低,为6%。验证了理论的正确性。
5 结 语
本文综合考虑齿槽效应和端部效应的影响,采用最优极弧系数和磁极倒角法削弱齿槽法向力波动,分别降低了21.53%和30.76%。然后,基于该结构优化铁心长度,削弱法向力波动43.07%,最大推力波动降低50%。最后,通过有限元方法优化端齿形状,3种措施下综合最大法向力波动比原电机降低了67.69%,而最大推力波动降低了75%,与此同时,推力均值降低了6%。所得结论可为PMLM的理论分析和设计提供一定的指导。
