无人机SAR数据低比特量化及其复杂度分析

李正茂，陈大庆，刘马良

1)合肥学院计算机科学与技术系，安徽合肥 230601； 2)太原卫星发射中心技术部，山西太原 030027；3)西安电子科技大学微电子学院，陕西西安 710071

无人机(unmanned aerial vehicle, UAV)与常规的飞行器相比，具有成本低、灵活性高、隐蔽性强、适应性强和功能多样等优势．随着UAV技术的发展与成熟，其在战场侦察、公安反恐、航空摄影、地质测绘、农业植保等领域日渐被广泛应用[1-2]．合成孔径雷达(synthetic aperture radar, SAR)作为一种主动探测手段，能够全天时、全天候地对目标场景进行高分辨成像，弥补了传统光电遥感手段的不足，进一步提升了UAV平台的信息获取能力．同时，UAV平台灵活多样的飞行模式能够为SAR系统提供更加丰富的成像模式．两者结合能够令人们在更加复杂的探测场景中，获取更加精细的场景信息，这进一步促进了UAV SAR系统在军用及民用领域的推广与应用．

SAR系统通常采用大时宽带宽积信号实现高分辨探测，需要较为复杂的数据采集、存储、处理和传输系统作为支撑．然而，UAV平台常因体积受限，难以保障充分的数据处理能力．因此，如何利用有限的硬件资源实现最大程度地保障信号处理的质量，是基于UAV的SAR系统需要解决的关键问题之一．较为传统的方法是采用均匀阈值进行量化，这种方法通用性较好，但为了减少量化过程中带来的信号幅度损失，通常需要较高的量化位数来对采样数据点进行表征，这无疑增加了后续数据处理的复杂度与成本．为解决这一难题，有学者针对SAR数据的特性，在降低SAR数据量化精度方面展开了研究．通常SAR回波数据能够满足高斯分布特性，基于这一假设，潘志刚等[3-4]提出分块自适应量化(block adaptive quantization, BAQ)方法，将SAR数据分为能够满足高斯分布特性的数据块，并在数据块内采用最优阈值降低量化位数，同时通过保留数据块的方差信息来恢复一定的SAR数据幅度信息．但这种方法依赖于回波数据的高斯分布假设，当数据不能满足该假设时，SAR成像质量会下降．为弥补这一缺陷，喻言等[5]提出基于矢量量化(vector quantization, VQ)的SAR数据量化方法，然而该方法仍需预先针对数据的统计特性对其量化阈值进行训练，无法从本质上降低数据采样的复杂度．FRANCESCHETTI等[6-7]提出基于单比特采样的SAR回波数据采集模型，并证明通过合理的阈值和参数设计，单比特采样量化数据能获得与高精度SAR回波数据相近的成像结果．但是，单比特采样需要有较高的采样率，而他们并未对单比特数据处理的复杂度进行分析．

本研究针对UAV SAR的低比特量化应用需求，分别基于传统均匀量化(uniform quantization, UQ)、BAQ及单频阈值(single-frequency threshold, SFT)单比特量化方法，分析成像质量，并对成像处理中最关键的匹配滤波步骤的运算复杂度进行定量描述，以期为低比特量化在UAV SAR系统中的应用提供支撑．

1 SAR数据低比特量化模型

为获得SAR图像，雷达接收机需要将自由空间中连续的SAR回波信号，转化为便于存储与处理的数字信号，再利用数字信号处理的方法实现回波数据到SAR图像的转化．将连续信号转化为数字信号的过程，需要对连续信号进行离散采样，并将具有大量可能的离散取值近似为有限的确定取值，该过程称为量化．量化位数的提高能够有效降低量化过程中引入的误差，但对数字信号进行存储与处理的复杂度也随之提升；较低的量化位数可以简化后续的数字信号处理过程，但随之而来的量化误差会降低SAR成像的质量．如何在SAR成像质量与数据处理复杂度之间达到较好的平衡，量化方法的选择至关重要．

1.1 均匀量化

设tr为快时间，s(tr)为SAR回波数据，对其进行量化的过程可表述为

Q[s(tr)]=g{⎣f[s(tr)]」}

(1)

利用实值函数f(·)对s(tr)进行变换后，通过⎣·」运算对其进行向下取整，即可实现量化操作．函数g(·)为f(·)的逆操作，可对量化后的信号进行恢复，恢复后的信号为Q[s(tr)]．

均匀量化是较常用的量化方法．若f(·)是一个比例函数，均匀量化就是利用一个固定的比例因子对信号s(tr)进行缩放，使其达到所需量化位数所对应的动态范围．假设信号被均匀量化比特数为K， 且其在所有的量化区间上均服从均匀分布，由于量化引入的误差也服从均匀分布，则信号量化噪声比(quantified signal to noise ratio, SQNR)为

SQNR=20lg 2K≈6.02K

(2)

由式(2)可知，每增加1 bit量化位数，可提升约6.02 dB的量化信噪比．

1.2 自适应量化[3-5]

SAR原始数据通常能够满足高斯分布特性，利用该统计特性，在有限的量化位数约束下，最小化由量化带来的数据失真．为此，需将回波数据沿距离维和方位维分成若干小块，每小块数据能够近似地满足零均值高斯分布．计算每块数据的方差δ， 再对数据块进行归一化处理．BAQ利用Lloyd-max量化[8-9]对归一化数据块进行处理，而块自适应矢量量化(block adaptive vector quantization, BAVQ)则通过预先学习量化矢量集来降低量化位数．总之，自适应量化器是以最小化量化误差为准则，设计最优的量化与重构映射，即f(·)与g(·)． 该问题可描述为

(3)

自适应量化能够利用有限的比特数，在最大程度上保证SAR回波数据的恢复质量，但其数据分块及方差δ的计算过程，仍需对原始回波数据进行高精度采样，这势必会消耗UAV平台上较多的硬件计算资源．

1.3 基于单频阈值的单比特量化[7]

基于单频阈值的单比特量化充分利用了SAR信号的特性，将SAR回波数据的量化位数降低至单比特，并通过引入单频阈值量化(single-frequency threshold quantization, SFTQ)，解决了单比特量化中信号相对幅度失真的问题，又通过SFT的频移特性削弱了回波信号高次谐波的影响，从而实现了单比特回波数据的高质量SAR成像．该量化模型可描述为

s1(tr)=sgn[s(tr)+hs(tr)]=

sgn(σcosφ+Ascosψ)+

j sgn(σsinφ+Assinψ)

(4)

其中，s1(tr)为1 bit量化的回波信号； sgn()为符号函数，通过取信号符号的方式可实现对回波信号的单比特量化；σ为目标的散射系数；φ和ψ分别为回波信号与单频阈值的相位；hs(tr)为单频阈值，其表达式为

hs(tr)=Asexp(j2πf0tr+j2πφ)

(5)

其中，As为单频阈值的幅值；f0为阈值频率；φ为阈值的初相．

符号函数的积分形式可表示为

(6)

其中，ξ为积分变量．由于式(4)涉及到SAR回波与单频阈值两个频谱分量，因此，单比特量化将分别引入它们各自的高次谐波分量，以及它们之间的交调分量，即

(7)

其中，m与n分别表示回波信号与单频阈值谐波的阶次； Jm(σξ)为m阶贝塞尔函数， Jn(Asξ)为n阶贝塞尔函数； 当m=n=0时,εm=εn=1， 当m≠0, 且n≠0时,εm=εn=2；Amn为SAR信号第m次谐波与单频阈值的n次谐波交叉调制后，所得谐波分量的幅度，且当m+n为偶数时，Amn=0, 当m+n为奇数时，Amn≠0[10]． 因此，单比特量化的结果仅包含m+n为奇数的谐波交调分量，即

(8)

该模型可进一步推广到低比特量化的情况，交调谐波分量的幅度会随着量化位数的增加而衰减．在实际应用中，为在低比特量化下保证SAR成像质量，需通过对阈值频率及信号采样率进行设计，对交调分量的频谱进行搬移，从而减弱其对SAR成像质量的影响．对不同参数下的谐波分布进行分析，并据此对单频阈值的参数进行选择[7]，可以得到如表1的4组可供选择的参数组．

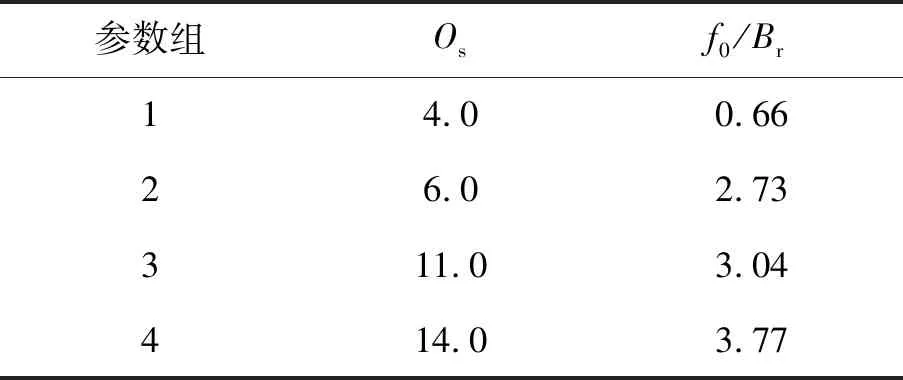
表1 低比特量化参数

其中，Os为过采样率；f0/Br为归一化阈值频率，f0为阈值频率；Br为SAR信号带宽．提高Os能够提供更大的频谱空间，以便容纳更多的交调分量，此时若能配合单频阈值频率的设置，可将危害较大的谐波分量搬移至SAR回波频谱之外的区域，从而达到改善单比特SAR回波数据成像质量的目的．虽然提升Os将导致数据量的增加，但也降低了低比特量化数据的处理复杂度．因此，本研究拟进一步分析低比特量化数据的处理复杂度，以便对系统的复杂度与成本进行定量描述．

2 低比特量化数据处理复杂度

在采集了回波数据后，SAR系统通常对数据进行脉冲压缩，以达到距离维高分辨的目的．脉冲压缩通常需要进行匹配滤波操作，该操作可通过将回波数据与匹配滤波器进行时域卷积实现，或将两者分别变换至频域进行频谱相乘实现．

频域相乘的方法需要在傅里叶变换前将SAR回波数据向量与匹配滤波器向量补零至相同的长度，补零的长度由两个向量中较长的序列决定，这无疑增加了数据处理的运算负担．此外，进行时域信号及其频谱转换的傅里叶变换和其逆运算，进一步提升了脉冲压缩的整体复杂度．然而，时域卷积的匹配滤波方法不需要进行补零操作，只需利用较短的序列对较长序列进行滑动卷积，因此，其数据处理复杂度由两个向量中较短的序列决定．同时，该方法不需进行频繁的时频转换操作，可有效降低脉冲压缩运算的复杂度．在此将基于时域卷积的方法对数据处理复杂度进行分析．

SAR系统发射具有大时宽带宽积的线性调频信号，相应的匹配滤波器则是具有相同时宽、相反调频率的宽带信号，其带宽与发射信号相同，也为Br． 因此，匹配滤波器的采样频率也应满足奈奎斯特采样定律．对复信号而言，则需Fs≥Br． 其中，Fs为采样频率．采样率过低将导致信号频谱混叠，从而难以有效地恢复SAR场景的真实信息；采样率过高则会导致回波数据量的剧增，为后续的数据处理带来困难．因此，在实际应用中，常定义过采样率Os来描述采样率与信号带宽的关系，即Fs=Os/Br． 通常选择Os=1.5， 即可满足应用需求．然而在针对单比特量化数据的处理中，则需采用更高的过采样率来保证最终SAR成像的质量，这会导致匹配滤波器长度的增加．但是，由于此时的回波是以低比特形式采集的，对其的处理也可大幅简化．

表2 乘法器所需晶体管数[11-14]

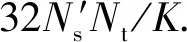
可见，匹配滤波卷积运算中取得晶体管总数为

(9)

在不同的量化比特数与采样率下，以晶体管数量表示的SAR回波数据匹配滤波运算复杂度如表3．在单比特SAR回波数据量化的方法中，提升采样率可使SAR成像结果达到与传统SAR成像相似的质量[7]，但同时也不可避免地增加了匹配滤波的计算复杂度．虽然成像质量的提升也可以通过提高量化精度的方式实现，但对高量化数据的处理复杂度要远远高于单比特数据处理的复杂度．如表3，即使是在较低的过采样率(Os=1.5，Os=4.0和Os=6.0)下，K=2 bit时的匹配滤波运算复杂度比已超过高采样率(Os=11.0和Os=14.0)下的单比特(K=1 bit)数据．随着K的进一步增加，对SAR回波数据进行匹配滤波处理的复杂度也显著增加．

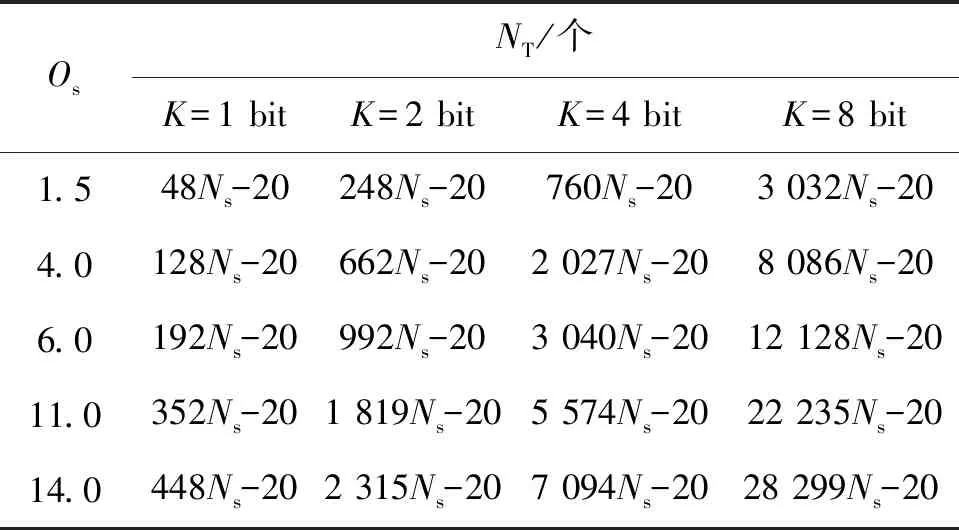
表3 匹配滤波运算复杂度

3 仿真实验及分析

利用美国桑迪亚国家实验室(Sandia National Laboratories)MiniSAR系统[15]获得的SAR成像结果，进行仿真对比实验．成像场景中包含建筑、树木和道路等丰富的目标．其中，建筑物是典型的人造目标，具有二面角、三面角等强散射结构，在成像结果中形成较强的散射点；树木的树冠部分也会形成类似结果，因此也有较强的散射特性；道路会对电磁波形成近似的镜面反射，因此在SAR图像中呈现为较暗的部分．场景中丰富的目标特性使得SAR成像结果具有较大的动态范围，从而可以对不同量化方法的性能进行有效的检验．

在常规的过采样率(Os=1.5)下，分别采用均匀量化、块自适应量化以及单频阈值量化的方法，将SAR回波数据量化为单比特，并分别对其进行成像处理，得到如图1结果(右下角为目标局部放大图)．由于单比特量化引入了SAR回波信号的高次谐波，谐波频谱在UQ、BAQ、BAVQ中与SAR原始信号的频谱重叠，从而在成像中形成散焦的虚像，造成SAR图像质量的下降(图1(a)、(b)和(c))．而单频阈值能够对高次谐波的频谱进行搬移，削弱其对SAR原始信号频谱的影响，改善单比特SAR回波数据的成像质量，从而在相同的参数下获得更为清晰的SAR成像结果(图1(d))．

当采用参数组4中较高的过采样率进行量化时，高采样率减少了高次谐波的混叠，因此能够在均匀量化与自适应量化中获得成像质量的提升(图2(a)、(b)和(c))．而单比特阈值则可将高次谐波分量移出成像频谱区域，令获得的SAR成像质量进一步提升，如图2(d)中目标局部放大图所示，单比特SAR回波数据在单频阈值的辅助下能够对目标的轮廓进行更清晰地呈现．

随着量化比特数的提升，均匀量化与块自适应量化能够保留更加丰富的信息，从而提升了成像性能．与此同时，由于量化引入的高次谐波逐渐减弱，单频阈值的优势也逐渐削弱．在不同量化比特数和不同参数下采用不同的量化方法进行实验，将所得成像结果与精确无误差的SAR成像结果比较，并计算两者之间的结构相似度(structural similarity, SSIM)，得到如图3的定量评估结果．

由图3可见，BAQ与BAVQ由于能够根据回波数据的统计特性调整量化阈值，因此能在低比特量化数据中获得优于UQ的SAR成像性能．而由于SAR场景中目标类型丰富，回波数据能够满足高斯分布，因此BAQ与BAVQ具有相似的成像性能．单频阈值能够在低比特量化中获得优于其他方法的性能，且通过提高采样率能够显著提升其性能，而其他方法并不能．随着量化比特数的增加，单比特阈值量化方法的优势将逐渐减弱乃至消失，而其他方法的性能均有所提升， 且BAQ与BAVQ能够在同样的量比特位数下获得优于UQ的性能．在较高的量化比特数下，不同量化方法的性能逐渐趋于精确的SAR成像结果，此时SSIM值将趋于1．因此，在无人机平台存储与数据处理资源有限的情况下，单频阈值低比特量化能够以较小的硬件开支获得较大程度的性能提升，有利于无人机SAR成像系统的低成本与小型化．当无人机平台具有较充足的资源可以利用时，则可通过提升量化比特数的方法来获得SAR成像性能的进一步提升．

图1 常规采样率下(Os=1.50)不同方法量化数据的单比特成像结果Fig.1 Single-bit imaging result obtained using different quantization with conventional sampling rate (Os=1.50)

图2 参数组4下不同方法量化数据的单比特成像结果Fig.2 Single-bit imaging result obtained using different quantization with parameter group 4

图3 不同量化精度与采样率下，采用不同量化方法成像结果的SSIM值对比Fig.3 (Color online) SSIM of SAR images with different quantization accuracies and sampling rates for different quantization approaches

结 语

针对UAV平台下SAR成像系统的微型化需求，对比分析了不同的低比特量化方法所需的硬件计算复杂度以及其能够达到的成像性能，定量的分析能够为UAV平台有限硬件资源的合理规划提供依据，从而能够根据UAV平台具备的数据处理能力选择合适的回波数据量化方法，充分利用有限的硬件资源获得尽可能高质量的SAR成像结果，为UAV平台下SAR系统设计提供参考．在未来的工作中我们将进一步针对UAV平台优化微型化SAR系统的实现方案，达到简化系统、提升性能的目的．