基于WPG的无人机一致性控制算法

彭 浩，毛祥荟，谷源涛，王永程，王 玉

1)清华大学电子工程系，北京 100084；2)盲信号处理国家级重点实验室，成都 610041

无人机(unmanned aerial vehicle, UAV)的一致性(consensus)控制是多智能体系统(multi-agent system, MAS)一致性控制研究中的一个重要问题．MAS指大量分散的自主或半自主的智能体通过网络互连所构成的复杂的大规模系统．每个智能体具有简单计算、信息处理与不完全通信的能力，在整个系统的交互式协调与配合下可实现一些复杂和智能的任务．多智能体的一致性控制是计算机科学与控制领域一直关注的热点，目前在飞行器的编队控制、传感器网络、数据融合、多机械臂协同装备与并行计算等领域被广泛应用[1]．MAS的一致性控制[2]指在没有中央控制及全局通信的条件下，系统内的多个智能体通过信息共享与交互，最终实现所有智能体的某种状态(如姿态、方向及高度等)趋同．

对MAS一致性的研究一般从系统动力学及网络拓扑结构两个角度进行．从动力学角度可将问题建模为线性系统或非线性系统进行研究．线性系统通常建模为一阶、二阶及高阶系统．通过分析特征值，已得到了一阶与二阶线性多智能体系统实现一致性的充分必要条件．对于一阶积分器，达到一致性的充分必要条件为当且仅当网络具有生成树[3]．而对于二阶系统，除了要求网络具有生成树外，拉普拉斯矩阵特征值和耦合增益必须满足其他条件[4]．REN等[5]得出了实现高阶线性积分模型一致性的充分必要条件, 为高阶线性系统一致性的研究奠定基础．从网络拓扑角度出发，通常考虑通信拓扑的不确定性对系统稳定性与动态性能的影响，包括通信时滞、随机网络及切换拓扑等因素．ZHANG等[6]分析了当网络是马尔科夫随机切换拓扑结构时, 系统达到均方一致的条件, 并给出基于线性矩阵不等式(linear matrix inequality, LMI)方法的随机系统的一致性算法．通过分析MAS通信拓扑，WIELAND等[7]分别研究了有领导者和无领导者情况下，线性MAS的一致性控制问题，并给出基于相对状态信息的一致性协议的设计方法．

2016年，明平松等[8]对随机时滞多智能体一致性研究进展进行了总结．DU等[9]将递归设计方法与加幂积分技术融合，使用递归方式构建李雅普诺夫函数，提出基于邻居的分布式高阶有限时间一致性协议，使领导-追随者系统不需领导者的速度信息就能实现有限时间一致．严志强等[10]针对多智能体一致性算法中的通信问题，提出一种近邻原则，利用部分二阶和部分三阶邻居信息，在固定无向连通拓扑图的基础上，应用于三阶MAS．朱美玲等[11]在固定与切换拓扑情况下分别给出了异构系统一致性的控制协议，得到了异构系统有限时间一致性的充分条件．

MAS的一致性问题在编队(vehicle formations)、高度对齐(altitude alignment)及集群(flocking)等场景被广泛研究[12]．近年来由于无人机技术的成熟与成本的降低，无人机在军事与民用领域的作用日益重要，无人机的一致性控制也成为研究热点．柳向阳等[13]提出基于多无人机目标估计的分布式无迹信息滤波，证明了基于有向图网络的加权平均一致性算法，构建了多无人机目标跟踪的模型．张佳龙等[14]基于人工势场方法，提出一种双向网络连接结构的多无人机一致性避障控制算法．张红梅等[15]针对无人机编队的通信拓扑切换，研究了一种基于联合误差的编队控制方法．

本研究提出基于WPG算法的一致性控制算法，利用高效率的分布式优化算法解决固定拓扑下的一致性问题，并通过在无人机的高度对齐场景下进行仿真，验证了算法的收敛性与低通信开销的特性．

1 WPG算法

游走近端梯度(walk proximal gradient, WPG)算法[16]是一种分布式一致性优化的一阶算法．多智能体系统可看作一个网络G=(V,E)， 其中，V={v1,v2, …,vn}是智能体集合，E为m条边的集合．WPG算法旨在解决如式(1)的一致性优化问题．

(1)

(2)

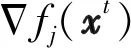
在无人机协同高度对齐这一场景下，为适应无人机集群中可能出现的无路由场景，本研究在WPG算法的启发下提出一种基于WPG算法的方法．在该方法中，当节点被激活时，采用后向梯度对局部变量进行更新，即

zt+1it=proxfi /α(xt)

(3)

对任意函数f及优化变量x，f的近邻算子为

(4)

调整后的方法是WPG算法在无人机高度对齐这一实例下的变种，标准WPG算法采用如式(2)的前向梯度更新，而这里采用如式(3)的后向梯度更新．调整后的方法只需在相邻节点间传递信息，可大幅节省通信开销．值得一提的是，虽然在此场景的目标函数f下，两种算法可以互推，但在一般情况的凸函数f下，两种算法并不等价，无法互推．

输入:令牌顺序I={i1, i2, …, in} 输出:共识量 x∗1 initialize x0 and z0 so that x0=12∑nj=1z0j2 repeat for t=0, 1, 2, … do3 agent it=modn(t)+1 do4 receive token xt5 update local variable zt+1it by (2)6 update token xt+1=xt+1n(zt+1it-ztit)7 send token xt+1 to agent it+18 agents j≠it do nothing; hence zt+1it=ztit9 end10output x∗=xt

图1 WPG算法(算法1)流程伪代码

Fig.1 Pseudocode of WPG algorithm (algorithm 1) flow

2 无人机协同高度对齐模型

高度对齐本质上是一致均值问题，在此特定场景下，式(1)所示的WPG算法的优化目标可写成：

(5)

其中，aj为各无人机所处高度；x是待优化的无人机的高度．

在此特定函数f下，当式(3)中α→0时，此变种算法可退化为标准WPG算法，即式(2)中α=1的情况．因此，算法在有路由及无路由情况下均可工作，下面分别介绍这两种情况．

2.1 有路由模型

定义场景中存在NC个无人机，每个无人机可看做网络G=(V,E)中的一个节点，V是无人机的集合．两个无人机之间能否直接进行通信决定了图中两个节点是否相连，E为两节点间通信链路的集合．在已知图中节点间路由的情况下，本研究可以设计对应的令牌顺序，按照算法1的流程进行分布式的一致性优化．

值得一提的是，WPG算法需要在网络G中遍历所有节点v∈V． 因此，需要先在网络G中确定一个汉密尔顿圈(存在的话)．假设网络G中存在一个汉密尔顿圈(1, 2, …,n)， 那么在WPG算法中便按照1→2→…→n→1→2→…的顺序进行信息传递与更新．若网络G中不存在汉密尔顿圈，则需确定一个至少遍历所有节点1次的圈(包含重复访问的节点)．在这种情况下，重复节点只在第1次被访问时激活，后续的重复访问将不再激活该节点．

2.2 无路由模型

考虑到实际情况中，路由的获得相对困难，一般需要付出高昂的通信代价，因此本研究对WPG算法进行推广，把原来信息传递与更新的单位由一个节点推广为一个簇(由若干节点组成的集合)．这是因为，一般来说簇头间的拓扑关系比整个网络要简单很多，簇头间的路由获取的代价相对较小．在此场景下簇头间的通信需要路由信息，而簇内的通信不需要路由．

模型目标是经过协同处理使所有无人机调整到同一高度x上，这可表示为一个优化问题，x为待优化的参量．首先，定义簇内目标函数为

(6)

其中，fl(x)为第l个簇的目标函数，表征当前待优化参量x与簇内nl个无人机高度的偏离程度，当x取最优解时，目标函数得到最小值．al, j为第(l,j)个节点的原始高度．每个无人机的簇之间只能通过簇头进行通信，不同簇中除簇头外的其他节点无法直接进行通信．因此，整个无人机群的目标函数可写作各个簇的目标函数累加的形式，即

(7)

将式(6)描述的目标函数代入式(3)，可得到其闭式解为

proxfl/α(xt)=

(8)

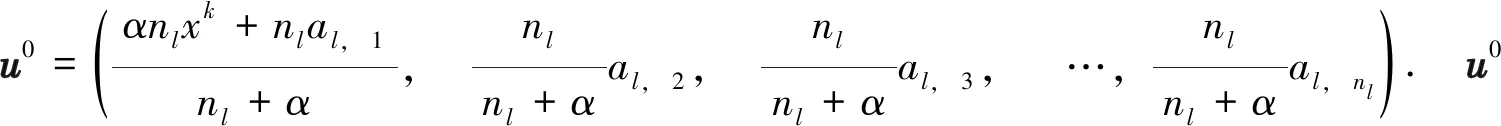
Gossip算法利用节点的本地信息处理能力，通过同步更新节点并与邻居节点进行数据交换的方式，使网络达到平均共识状态，从而避免了网络中路由的开销和瓶颈效应．

(9)

其中，i和j分别指第l个簇中节点的编号；di为节点i的度，k为与第i个节点邻接的节点编号．

在得到拓扑矩阵P后，每次迭代中以待优化向量u乘上P， 在经过足够的迭代后，u会收敛到初始值的均值．由P的约束关系可知，P中非邻接节点对应位置的值为0，这就保证了在每次迭代中实际上只需与邻接的节点间进行信息交换即可，故可减少通信开销．Gossip算法流程的伪代码如图2．

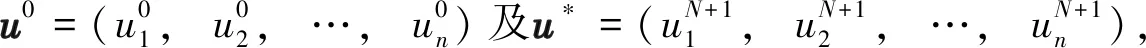
(10)

输入:拓扑矩阵 P输出:共识向量 u∗1 initialize u02 for t=0 to N do3 ut+1= ut·P4 end5 output u∗=uN+1

图2 Gossip算法流程伪代码

Fig.2 Pseudocode of Gossip algorithm flow

利用基于Gossip的方法，在每个簇进行更新时，簇内每个节点只需与其邻接的节点之间进行信息交换即可．在进行N次信息交换后，簇内所有节点均收敛到一致值，也就是均值．

簇头间路由的策略非本研究的重点，可采用已有算法．例如，若簇头组成了汉密尔顿网络，则可采取基于汉密尔顿圈的通信策略[17-18]．而对于强连接的网络，也有很多路由策略，如采取基于最短路径的策略[19-20]．

3 实验仿真与分析

通过仿真实验，对比本研究提出的基于WPG的无人机一致性控制算法和不使用WPG的算法，针对高度对齐场景的应用，验证本算法在通信效率方面的性能．

实验使用3个无人机群，每个机群分别包含4、5和6个无人机，共15个节点，每个簇之间通过簇头通信，其拓扑关系如图3．其中，相同灰度的节点属于同一个簇．无人机的初始高度满足[20, 120]内均匀分布．计算机仿真在Matlab R2017a环境下进行．

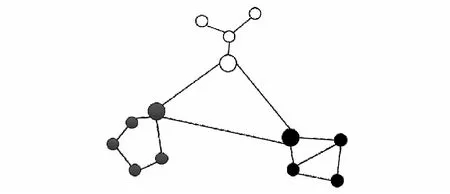
图3 无人机群拓扑Fig.3 Topology of UAV clusters

3.1 有路由情况

在使用一些路由算法及付出相应的通信开销后，可获得无人机群通信的路由．在有路由的情况下，可直接应用以单个节点为单位进行信息传递更新的方法，即信息按照路由每次在各个无人机间进行传递与更新．初始化设x0=z0=0， 最大迭代次数设为30．

在有路由的情况下，基于WPG的算法收敛速度如图4．由图4可见，信息令牌在15次更新后，亦即在所有无人机节点间传递一遍后收敛于所有无人机初始高度的均值．在已知路由的情况下，本算法在有限步内精确收敛到最优解．若无人机总数为NC， 则算法在NC次迭代后收敛，且相对误差在10-16以下，也就是说，完成信息令牌在所有无人机间的1次传递即可．

图4 有路由情况下WPG算法的收敛性曲线Fig.4 Convergence of WPG algorithm without routing

3.2 无路由情况

由于获取路由的开销往往较大，在缺少簇内路由，但可得到簇头间路由的情况下，应用上述以单个簇为单位进行信息传递更新的WPG算法．即信息每次在各个簇的簇头之间进行传递与更新，在簇内通过基于Gossip迭代方法收敛到簇内的一致值．初始化设x0=z0j=70,j=1, 2, …,n,α=90， Gossip算法的迭代次数N=45．

无路由情况下基于WPG的算法收敛速度如图5(a)．从图5(a)可见，本算法收敛性佳，信息令牌x在200次更新后就收敛到无人机群的一致值，且相对误差在10-3以下，远低于无人机厘米级的控制误差．

由于在通常情况下，相对于簇间的通信开销，簇内的通信开销可以忽略，因此，以簇间的通信次数作为衡量通信开销的指标．从图5(b)可见，在引入WPG算法后，通信效率得到大幅提升，在同样的误差下，引入WPG算法的通信开销要远小于改进前的算法．原因是改进前的算法在每次迭代时需更新所有的簇头信息，而改进后的算法在每次迭代时只需更新一个簇头信息．同时观察到，当基于WPG的算法收敛时，在同样的通信开销下，基于WPG算法的均方误差要比改进前减小23 dB．

图5 无路由情况收敛性及通信开销Fig.5 Convergence and communication overhead without routing

结 语

本研究将分布式优化算法WPG引入到无人机的一致性控制问题中，并在高度对齐场景中进行建模仿真．在有路由的情况下，算法可在有限步内很快收敛，且收敛的精度很高；在无路由的情况下，将WPG算法进行推广并与Gossip方法结合．推广后的算法仍然具有很好的收敛性，并具有很高的通信效率，可大幅节约通信开销．