运载火箭整流罩脉动压力环境的数值模拟研究

李凰立，苏 虹，沈 丹

（北京宇航系统工程研究所，北京，100076）

0 引 言

脉动压力是一种随时间变化的压力，所以当其作用于火箭上时，脉动压力是不均匀的，很可能对某个部位产生较集中或较大的压力。同时，非定常流体因脉动也会产生气动噪声，在航空航天工程中，大量试验研究表明：脉动压力激起的气动噪声的幅值一般在130～170 dB，频率覆盖了低、中、高频。通常将5～100 Hz的振动视为低频段，将20～2000 Hz的振动称为高频段（高、低频不只是以频率大小分类，还与振动机理有关）。火箭壳体的频率一般较低，低频段的脉动压力往往会激起结构的强烈振动，造成设备破坏。非定常脉动引起的噪声在向外传播的同时，也会传入飞行器内部，以宽带噪声的形式影响舱内仪器或者工作人员。如果噪声频率与箭体特定模态的频率范围接近时，就有可能导致箭体结构的疲劳甚至破坏，因此火箭结构强度设计必须考虑脉动压力的影响。

飞行试验经验表明，脉动压力在火箭跨声速段至最大动压时间段较大，随着火箭高度增加（空气密度减小）逐渐减小。因此，脉动压力研究的重点在跨声速时段。但是，无论是开展风洞试验模拟还是工程预示、数值模拟，跨声速脉动压力的研究难度都很大，尤其是数值模拟，对分析方法和数值算法都提出了较高的要求。跨声速脉动压力主要因强激波/边界层相互干扰而产生，体现在激波位置的前后移动和强激波后的非定常流动分离等多方面。当前学术界对脉动压力的非定常数值模拟大多为直接数值模拟（Direct Numerical Simulation，DNS），但是DNS在现有计算条件下只能分析小雷诺数情况下的流动，对于高雷诺数DNS计算量计算时间过多；大涡模拟法（Large Eddy Simulation，LES）也是非定常模拟方法，它可精确计算大尺度非定常运动及分离流动，然而模拟边界层流动时，LES所需计算资源也很大，且近壁模式不成熟，还需发展和完善；雷诺平均法（Reynolds Average Navier-Stokes，RANS）求解Reynolds平均的Navier-Stokes方程组，可以较好地模拟附体流动，且对计算资源需求相对较低，但缺点是依赖于经验参数，湍流信息少，高频小尺度运动模拟不准，即便获得部分非定常效应，其可信度也不高。

鉴于LES和RANS都存在各自的优势和局限性，因此若能有机结合两种或多种方法的优点并利用自身的优点克服对方的不足，就有可能实现计算精度和效率的统一。RANS/LES的混合方法即具备上述特征。本文主要采用了RANS/LES方法分析脉动压力，实践证明算法有效、数据可信、规律合理。

1 计算方法

为了准确并且比较快速地预测跨声速飞行器的压力脉动，如下的关键技术需要首先解决：预测非定常特性的时间推进方法，预测非定常湍流方法。

1.1 预测非定常流动的高精度非定常时间推进方法

首先采用有限体积方法，按照某种空间格式离散Navier-Stokes方程组，将其转化成为每个网格单元上关于时间的一阶常微分方程组。对常微分方程组进行时间推进求解时，一般采用显式格式或隐式格式。

显式时间推进简单，易于实现，占用内存较少，工程中较为实用且应用广泛。但是显式推进格式有其自身固有的缺陷：受稳定性限制，CFL数不可取得太大，时间步长较小。在模拟非定常流动时，往往关心流动随时间的变化过程，如果使用显式方法，时间步长可能取得很小，导致计算效率降低。

相比之下隐式方法可取较大的全流场统一时间步长，计算效率较高，常用的隐式方法有LU-SGS分解方法，基本思想是将块对角矩阵分解为上、下两个三角矩阵，避免了繁杂的矩阵运算，节约了计算时间，可用于定常或非定常流动计算。但是 LU-SGS分解方法是一阶时间精度，为了充分发挥LU-SGS隐式方法的优势，提高模拟非定常流动隐式推进过程的时间精度，现采用伪时间子迭代技术（Pseudo Time Sub-iteration，τTS），也常被称作双时间推进技术。通过在原控制方程中引入伪时间导数项，即采用双时间方法，借助伪时间方向的“子迭代”技术，对LU-SGS隐式方法进行改进，使其达到二阶时间精度（本文简称为 LU-SGS-τTS）。

有限体积法离散后的N-S方程式为

式中 Q为守恒变量向量；S为源项，如无源项则S=0；I·n为净通量，且，

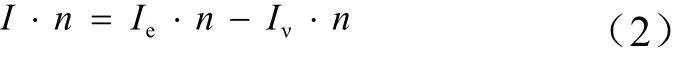
式中e·In为无粘通量；ν·In为粘性通量。

其半离散格式为

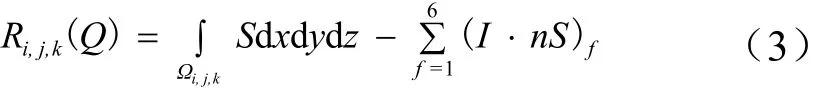
时间方向采用向后差分离散，得到：

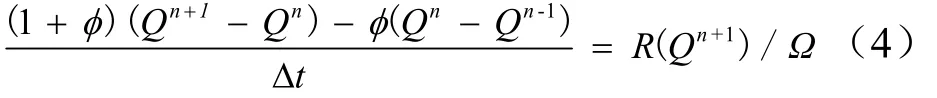
当φ=0.5时，时间方向上可以实现二阶精度。

引入了虚拟时间项之后可以计算非定常流场。下文即采用二阶精度 LU-SGS-τTS方法，根据经验、计算精度和计算效率，子迭代步数选取为3步。

1.2 预测非定常流动的湍流模拟方法

RANS在时间域上对流场物理量进行雷诺平均化处理，然后求解所得到的时均化控制方程。比较常用的模型包括S-A模型、k-ω模型、k-ε模型。雷诺时均模拟方法可以较好地模拟附体流动，精度基本可以满足工程需要，且计算效率高，对计算资源的需求相对较低；但RANS的缺点是只能提供湍流的平均信息，对于火箭关键部位的非定常脉动压力预测，给出的结果不够准确，不能很好地捕捉跨声速激波/边界层相互干扰的非定常特性。

LES属于湍流计算方法中的尺度解析模拟方法，主要是对流场中一部分湍流进行直接求解，其余部分通过数学模型来计算。LES方法在求解瞬态性和分离性比较强的流动中，相对RANS具有优势，LES可以准确地模拟分离流动；但LES方法对流场计算网格要求较高，特别是近壁面区域网格密度要求大于 RANS方法，在计算边界层流动时却需要耗费极大的计算资源。

RANS/LES混合方法结合RANS、LES两种或多种方法的优点并利用自身的优点克服对方的不足，可有效实现计算精度和效率的统一，即RANS用湍流模式高效且比较可靠地模拟高频小尺度运动占主导地位的近壁区域，LES方法可比较准确地计算低频大尺度运动占优的非定常分离流动区域。采用RANS/LES混合方法是当前计算资源有限情况下的合理选择，从工程应用角度分析，它也被认为是结合LES方法处理高雷诺时数下非定常流动的一种切实可行方法。

此外，在湍流模型上，本文采用了SST k-ω模型。SST k-ω模型混合了k-ω模型和k-ε模型的优势，在近壁面处使用k-ω模型，而在边界层外采用k-ε模型。SST k-ω模型包含了修正的湍流粘性公式，考虑了湍流剪切应力的效应，一般能更精确地模拟逆压梯度引起的分离点和分离区大小。

本文研究的主要途径就是采用基于 SST k-ω模式的RANS/LES方法，数值分析了跨声速飞行器头部区域流动中产生的非定常激波/边界层相互干扰，包括流动分离、激波位置振动等问题。

2 计算模型

以图 1所示的火箭头部为例，该外形头部采用结构化网格，网格形式见图2，采用的是O - C型结构网格。该网格的优点在于此种拓扑结构既保证了物面附近较高的网格密度，又可以使整个流场空间内保持合理而又均匀的网格分布。该网格体流向布置 330～350网格点，在外形变化剧烈的位置加密网格点；法向布置90～120网格点，贴近壁面处加密到10-3m量级；周向120～150网格点，背风面较密。据此计算，总网格点数目大约在520万左右。

图1 火箭头部外形示意Fig.1 Launch Vehicle Fairing Contour

图2 计算网格示意Fig.2 Grid Topology On Fairing

另外，为了便于下文将计算数据和试验数据对比，此处附上风洞试验的外形设计，见图3。模型设计中，在火箭头部柱段和倒锥段各选取一个测量截面。

图3 风洞模型测点和截面位置示意Fig.3 Wind-tunnel Model and the Station of the Fairing

3 计算状态和计算结果

以工程经验判断，火箭在飞行过程中强烈的脉动压力环境出现在跨声速阶段。对图1所示火箭头部外形，开展了若干跨声速状态下的脉动压力预示。表 1列出几个典型的马赫数和攻角组合状态。表1中同时还说明了对应状态下的流动特征。

表1 典型计算状态Tab.1 Typical States of Computation

下文分析各状态计算结果，其中脉动压力结果均已经过特定参考值无量纲化处理，包括后文试验数据。

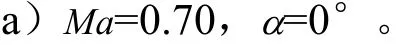
本状态计算所得最大均方根脉动压力系数大致在1.5%左右，且其位置在流向截面Ⅰ附近，与真实流动物理特性相符。脉动压力系数反映了脉动压力的强弱。图 4给出瞬时流场图，分别是表面流线、物面压力分布、速度梯度二阶不变量Q等值面，可见流动具有强非定常特性，尤其是通过湍动能变化，可看出最大脉动压力区域明显在截面Ⅰ之后。

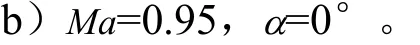
该状态攻角同样是 0°，但相比状态Ma=0.70，α=0°，马赫数为0.95更接近1，此时发生大振幅脉动压力的位置在倒锥段即流向截面Ⅱ之后，见图5。

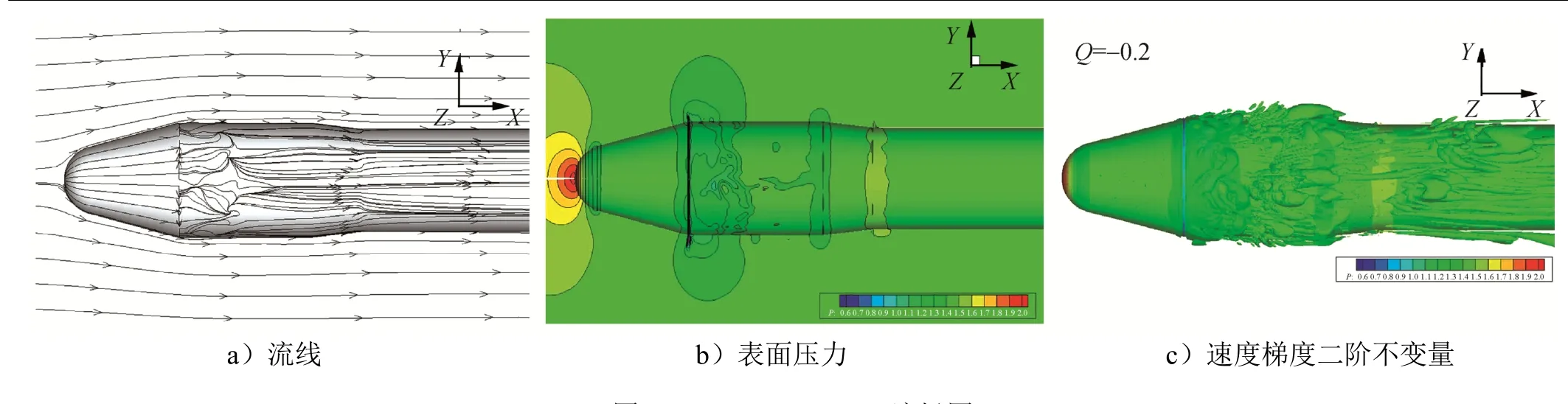
图4 Ma=0.70，α=0°流场图Fig.4 Flow Field of Ma=0.70，α=0°

图5 Ma=0.95，α=0°流场图Fig.5 Flow Field of Ma=0.95，α=0°

通过压力等值线图可以看出，头部前锥-柱段的激波位置往复移动，因此作用在火箭头部的力也来回变化，它与火箭结构相互作用会产生结构噪声；同时会形成非定常的俯仰力矩，导致火箭压心位置变化，影响火箭的稳定性和操纵性。

另外，图5显示前锥-柱段流动变化不大，存在很多类似小波纹的涡流结构，但是在倒锥段的湍动能则变化剧烈。在倒锥段，由于收缩外形导致流动扩张产生更强的激波/边界层干扰，强激波导致流动大范围分离，所以该部位的压力脉动最大。经统计了解到，截面Ⅰ均方根脉动压力系数大致为0.3%～0.5%，截面Ⅱ部分测点均方根脉动压力系数达到1.6%以上，这说明在接近跨声速Ma=1时，脉动压力较高能量已经后移至箭体柱段-倒锥段（截面Ⅱ之后）。

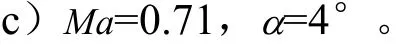
相比状态 Ma=0.70，α=0°，此状态有4°攻角，火箭整流罩头部的流动会出现上下不对称现象，即上下对称面的激波/边界层干扰会不同，见图6。

通过压力脉动幅值可见，背风面的漩涡比较集中，背风面分离区域较大，湍动能占优；但是激波强度并不大；因为攻角造成了流动在背风面分离，所以从截面Ⅰ开始，脉动压力就明显增大，经统计，截面Ⅰ最大均方根脉动压力系数约为1.3%；但是到截面Ⅱ之后，脉动压力的能量已经大幅减弱，均方根脉动压力系数逐渐变小，截面Ⅱ之后均方根脉动压力系数大致只能达到0.2%。

图6 Ma=0.71，α=4°流场图Fig.6 Flow Field of Ma=0.71，α=4°

该状态Ma=0.96，和状态Ma=0.95接近，因此流场特性差异主要由攻角大小差异决定。该状态流场如图7所示。

对比图 5（Ma=0.95，α=0°）、图 7（Ma=0.96，α=4°）流线特征，可知有攻角时，流动分离会发生在火箭整流罩头部较前区域；而对比之前计算状态，0°攻角时流动分离会发生在倒锥段之后。

图7 Ma=0.96，α=4°流场图Fig.7 Flow Field of Ma=0.96，α=4°

状态 Ma=0.96，α=4°的最大均方根脉动压力系数出现在截面Ⅰ附近；对比之前状态 Ma=0.95，α=0°最大均方根脉动压力系数出现在截面Ⅱ附近。

另外，由于存在攻角，所以状态Ma=0.96，α=4°在整个背风面的区域内，脉动压力的作用都比较明显。

图8 Ma=0.72，α=6°流场图Fig.8 Flow Field of Ma=0.72，α=6°

本状态攻角已经达到 6°，相对 0°攻角、4°攻角，本状态的迎风面激波更强、背风面出现漩涡。当攻角为 6°时，漩涡已经清晰可辨，从图 8的流线分布中可以观察到一个漩涡中心。另外，攻角6°时，湍动能在漩涡区域内的形态也更加丰富，和流动速度相关的Q值也充分反映了流动中漩涡的发展和演化。

该状态脉动压力较大区域产生在流向截面Ⅰ处，此时最大均方根脉动压力系数约为1.3%，基本在迎风面和背风面交界处。对称背风面上压力样本点的均方根脉动压力系数值大约为0.5%，由此体现攻角对压力的影响，反映了激波/边界层/漩涡的相互作用。

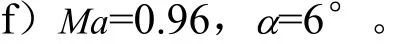
该状态可以和状态Ma=0.72，α=6°进行不同马赫数、相同攻角的对比；可以和状态Ma=0.95，α=0°、状态Ma=0.96，α=4°进行相同（相近）马赫数、不同攻角的对比。流场图参考图9。

相对状态Ma=0.72，α=6°，本状态均方根脉动压力最大的截面是截面Ⅱ，尤其是在背风面，部分点均方根脉动压力系数达到0.7%，较大的压力脉动来源于激波边界层相互作用；相对状态Ma=0.95，α=0°、状态 Ma=0.96，α=4°，本状态攻角6°背风面的旋涡比、4°情况更加集中，背风面分离区域范围更远，影响面积也更大；同时背风面湍动能占优。在压力场的图中可以看到，截面Ⅱ之后，伴随着较大的攻角，在背风面扩张角较大的地方容易产生空化、涡脱落现象，最终导致了背风面压力场的不稳定，并且使这一区域保持了较大的压力脉动。

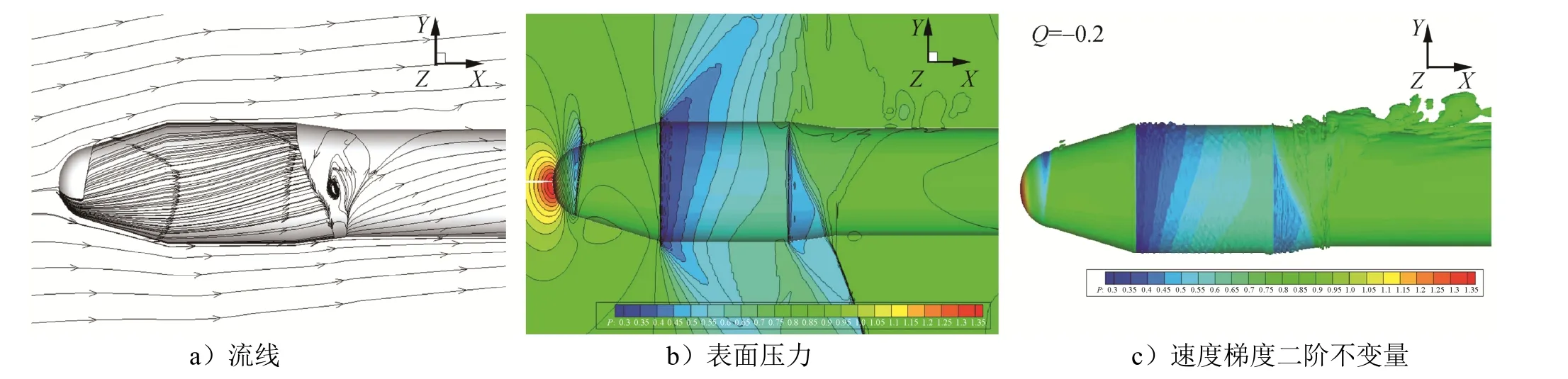
图9 Ma=0.96，α=6°流场图Fig.9 Flow Field of Ma=0.96，α=6°

4 数值预示果和风洞试验的对比

风洞试验和数值计算相辅相成，同时也是验证计算方法可靠性的重要手段。针对上述计算外形开展风洞实验，下文将数值计算统计的均方根脉动压力系数峰值结果和试验结果进行了比较，见表2。经比较可知：0°攻角时计算结果和试验结果符合较好，有攻角时的计算结果与试验结果差异比较明显；这说明流动分离过程复杂，模拟比较困难，目前建议分离区的计算需要在背风面加密网格，改进背风面近壁网格质量，提高数值算法的精度，以辨识较大脉动压力信号。

表2 数值计算结果与风洞试验数据对比Tab.2 Computation Results vs Wind-tunnel Data

5 结束语

针对跨声速脉动压力提出了一种非定常计算方法，含双时间推进技术和RANS/LES混合湍流模拟方法。通过几种典型状态的数值模拟，了解到：外形变化剧烈的表面更容易引起较大的脉动压力；这些变形剧烈的区域或位置在火箭高速上升的同时，将引起强烈的流动分离，在一定的马赫数和攻角的状态下，部分扩张段在下游流场将产生或强或弱的激波，且随着时间的推移前后振动，从而产生或大或小的脉动压力。

通过上述计算结论可知，当火箭以跨声速飞行时，流动是极不稳定的；尤其是在火箭头部外形变化的部段，例如锥-柱、柱-倒锥等外形变化部段，流场在强激波/边界层相互作用下，流动极易分离，分离流再引发激波前后不规则移动，由此将形成非定常的激振力，严重时诱发箭体的非定常结构响应即抖振效应。在马赫数从亚跨声速增加至跨声速的过程中，抖振会越加明显，当攻角不为0°时，抖振的影响还将更加复杂。抖振存在诸多负面影响，如影响火箭的气动、稳定和操纵性能、加速火箭结构疲劳，严重时会引起全箭结构振动，还有前文提及的气动噪声等不利影响，这些都应该引起火箭设计者的重视，在研制阶段需要落实相应的解决方案。

最后需要说明的是，本文对跨声速脉动压力的数值研究方法，还有一些待改进的空间：a）当开展有攻角计算时，背风面的旋涡比较集中，背风面的分离区域更大，因此背风面需要加密背风面的网格数量、改进近壁面网格质量；b）需要从湍流数值算法、网格设计方法等方面进行改进；c）结合相关外形的跨声速脉动压力风洞试验、或者飞行试验数据做出进一步的修订。