基于Duhem前馈逆补偿的压电陶瓷迟滞非线性自适应滑模控制*

徐子睿,许素安,富雅琼,洪凯星,徐红伟

(中国计量大学机电工程学院,杭州 310018)

压电陶瓷由于其体积小,响应快,定位精度高等优点,是目前微定位系统比较理想的驱动元件[1-2]。但是其自身具有的迟滞特性,对定位精度影响较大。为了降低迟滞特性对定位系统的定位精度的影响,国内外学者提出了许多迟滞模型和控制方案。比较常用的迟滞模型有Preisach模型[3-5],PI(Prandtl-Ishlinskii)模型[6-7],Bouc-wen模型[8-9],Duhem模型[10-11]等。Preisach模型是广受关注的模型,但是二次积分项的存在使其计算过程十分复杂,求逆繁琐.PI模型由Preisach模型简化而来,但不易根据实测数据来调整模型.Bouc-wen模型可以用来描述大多数的迟滞现象,设计控制器方便,但输入形态有限制对结果影响较大。Duhem模型的描述比较符合压电陶瓷非线性的动态性能,函数表达式明确,包含迟滞输入与输出的导数项,是一个动态模型,且仅当迟滞输入方向发生 改变时,其输出特性才会改变,方便建立逆模型.控制策略一般有:滑模控制,自适应控制,滑模自适应控制等。SU等学者将迟滞看做扰动,设计了一种鲁棒自适应控制器对其进行补偿[12]。但是直接控制方法增加了闭环对扰动进行抑制的负担,且非线性方法设计也较为复杂。而将逆模型作为前馈控制器可以一定程度上减弱压电陶瓷的非线性,也便于在此基础上设计控制器。滑模控制具有快速响应,对参数变化和扰动不灵敏,无须系统在线辨识,实现简单等优点,可以避免实际系统中许多不确定因素的影响。自适应控制是一种能修正自己特性以适应对象和扰动动态变化的一种控制方法,压电陶瓷的迟滞非线性与输入信号的频率有关,且本身对扰动十分敏感,所以将滑模控制与自适应控制相结合,理论上可以达到很好的控制系统性能。

本文选用Duhem逆模型作为前馈控制器,与自适应滑模控制相结合对压电陶瓷进行迟滞补偿控制。首先,根据实验所得的输入输出数据,应用递推最小二乘法对Duhem模型中的未知参数进行辨识,然后,根据辨识结果建立Duhem逆模型。由于压电陶瓷的迟滞非线性与输入信号的频率有关,且本身对扰动十分敏感,故设计自适应滑模控制器构成闭环控制,最后,将Duhem逆模型作为前馈控制器,与自适应滑模控制相结合,进一步提高系统的跟踪精度和鲁棒性。

1 迟滞位移的测量

利用实验室设备(详见5),对压电陶瓷的迟滞位移进行测量。每10 s改变5 V输入电压,电压变化范围为0～30 V;每15 s改变5 V输入电压,电压变化范围为0～50 V;每10 s改变1 V输入电压,电压变化范围为0～60 V。每500 ms采集一次数据,并对同一电压下的位移值取平均值减小测量误差。根据上述实验得到的迟滞位移与相应的电压值,通过MATLAB绘制压电陶瓷的电压-位移曲线,如图1所示。

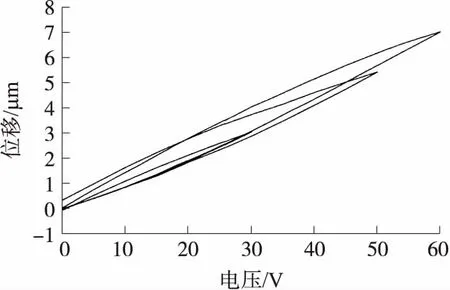
图1 压电陶瓷的电压-位移曲线

从图1中我们可以看出压电陶瓷具有明显的迟滞非线性,通过建立其迟滞逆模型作为前馈控制器,可以一定程度上减弱迟滞非线性。

2 迟滞模型及其逆模型的建立

2.1 Duhem迟滞模型的建立

Duhem模型的函数表达式比较清晰简明,模型中参数的不同变化可以反映不同的迟滞特性,准确辨识出模型中的各个参数,即可得到Duhem模型。Duhem模型可以写成如下微分方程表达式[13]:

(1)

式中:ɑ是常数,v是迟滞输入,w是迟滞输出,f,g定义为分段连续函数。

(2)

式中:

(3)

(4)

令Fi=αfi,(i=0……4),则式(2)可以写为:

(5)

为了便于辨识,将式(5)离散化,dw=w(k)-w(k-1),dv=v(k)-v(k-1),式中w(k)是系统k时刻的输出,v(k)是系统k时刻的输入。

令V1=|v(k)-v(k-1)|,V2=v(k)-v(k-1),Y(k)=w(k)-w(k-1),则式(5)可以写为如下形式:

(6)

系统的输入v、输出w及其导数是可测的,式中α,Fi=αfi,(i=0,…,4),gj(j=0,…,3)为系统参数;只要准确辨识出α,Fi,gj就可以得到Duhem模型。利用递推最小二乘法[14-15]可以很容易得到上述参数,辨识结过程如图1所示,横坐标为递推辨识的次数,纵坐标为参数的值。可以看出,模型中各参数在第221次估计后趋于稳定。取ɑ=0.017 200;f0=-1 201.765 556;f1=125.796 568;f2=3.119 384;f3=-0.080 180;f4=0.000 692;g0=107.390 783;g1=-1.417 493;g2=0.071 795;g3=-0.000 881。

根据实验测量的数据得到测量位移曲线,对取上述参数的Duhem模型输入与实验时相同的电压值得到拟合位移曲线,如图2所示。其中,实线为测量曲线,虚线为拟合曲线。

图2 Duhem模型参数辨识过程图

图3为拟合误差,表明绝对误差不超过0.12 μm。

图3 系统迟滞曲线与拟合曲线

2.2 Duhem迟滞模型逆模型的建立

建立逆模型的目的,是使用其作为前馈控制器,若用M[v(t)]表示正模型,M-1[w(t)]表示逆模型,则期望信号先后经过前馈控制器和被控对象可以用式(7)表示:

w=M{M-1[w(t)]}(t)=1

(7)

即理想状态下的传递函数为1,输出信号完全复现输入信号。因此,建立较为准确的逆模型有利于对迟滞系统进行有效补偿。

基于逆函数定理,Duhem模型的逆模型可以表示为如下形式:

(8)

(9)

式中:v为逆模型的输入,w为逆模型的输出,式(8)和式(9)中的参数与式(2)中的参数相同,只需将2.1中的得到的辨识结果代入式(8)和式(9)即可得到Duhem模型的逆模型。

3 自适应滑模控制器设计

滑模变结构控制具有算法简单,可靠性高等优点,自适应控制可以适应控制对象的动态变化,两者结合并与逆模型前馈控制器一同组成如图4所示的控制系统。其中,补偿电压uoff由前馈逆模型得到,系统误差e由实际输出wr与期望输出wd做差得到,并作为滑模控制器的输入。前馈控制器输出的补偿电压uoff与自适应滑模控制器输出的电压usmc共同组成广义被控对象的控制电压u。

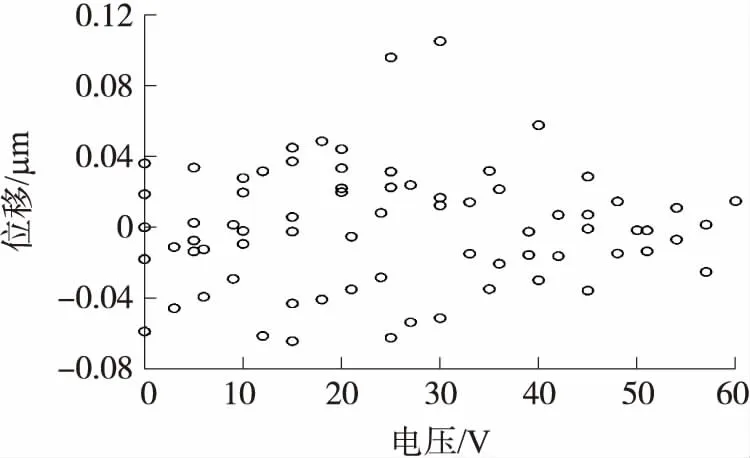
图4 拟合误差

图5 前馈结合自适应滑模控制系统框图

3.1 自适应滑模控制律及Lyapunov稳定性分析

根据文献[16],在低频工作区间内可以将压电陶瓷的传递函数简化为一阶惯性系统:

(10)

式中:T为时间常数,Δ为扰动,假设Δ有界,|Δ|≤D,D>0为扰动上界。

用θ代替T,则式(9)可以写为

(11)

定义系统误差为

e=wr-wd

(12)

定义滑模函数

s=Ce

(13)

令C=1>0,满足Hurwitz条件。则有

(14)

将式(10)代入式(13)可得

(15)

设计滑模控制律为:

usmc=ua+us1+us2

(16)

控制律usmc各项表示为:

(17)

us1=-kss

(18)

us2=-ηsgn(s)

(19)

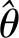
定义Lyapunov函数为

(20)

(21)

取自适应律为

(22)

则有

-kss2-ηsgn(s)s+Ds<-kss2≤0

(23)

为了减小抖振带来的影响,使用饱和函数sat(s)来代替符号函数sgn(s)。

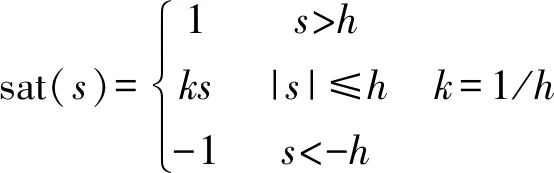
(24)

式中:h称为边界层,饱和函数的本质为:在边界层外,采用切换控制,在边界层内,采用线性化反馈控制。

4 仿真分析

根据实验输入输出数据,选择T=8,ks=400,γ=30,θ=0.11。利用Simulink对上述系统进行仿真,结果如图6所示。

图6 自适应滑模控制仿真结果

图6中,虚线为理想曲线,实线为跟踪曲线。从图6可以看出两条曲线几乎重合,选取3 s附近的曲线细节如图7所示,可以看出跟踪曲线实际上是在理想曲线的上下波动,误差小于1‰,说明了该控制算法的有效性。

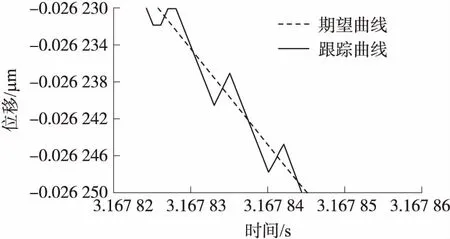
图7 自适应滑模控制仿真结果细节

5 实验分析

压电陶瓷位移测量采用双频激光外差干涉法,具有抗干扰能力强、可溯源性等优点。该系统由激光管、干涉仪光学组件、测量机箱、上位机、压电控制器、压电陶瓷等组成[17]。

实验所需设备如图8所示。激光管的型号为ZYGO ZMI7702,可以输出两束偏振光,它们的偏振方向互相垂直,频差为20 MHz,用于位移测量;双程干涉仪的型号为7006A。测量机箱的型号为ZMI2000,为激光管和数据采集卡提供电源,并提供与外部设备的通讯接口;上位机使用Labview编写,获取压电陶瓷的位移数据以及控制压电控制器产生驱动电压;压电控制器的型号为THORLABS BPC301,可提供0～150 V的驱动电压;压电陶瓷的型号为THORLABS AE0505D16F,其理论分辨率为100 nm/V,输出位移为0～17.4 μm,最大驱动电压是150 V。此外,为了减小环境对实验的影响,该测量系统还采用了气浮隔震台,型号为SPFO-I-B,其固有频率在垂直方向小于1.5 Hz,水平方向小于2 Hz。

图8 实验设备实物图

5.1 迟滞补偿实验

采用前馈与自适应滑模控制结合按照电压与位移1∶100的关系进行迟滞补偿实验,每隔15 s,改变10 V电压,每500 ms采集一次数据,得到图9。图中虚线为控制前的时间-位移曲线,实线为控制后的时间-位移曲线。图9表明,控制前迟滞特性明显,控制后同一电压下的位移量基本一致。迟滞得到了抑制。为了减小测量误差,将同一电压下的所有位移测量值取平均并绘制电压-位移曲线,得到图10和图11。图10为控制前的电压-位移曲线,图11为控制后的电压-位移曲线。控制前的最大迟滞量为1.281 7 μm,控制后最大迟滞量为0.049 4 μm,减小了96.1%,迟滞得到了有效的抑制。

图11 控制后时间-位移曲

图9 控制前与控制后的时间-位移曲线

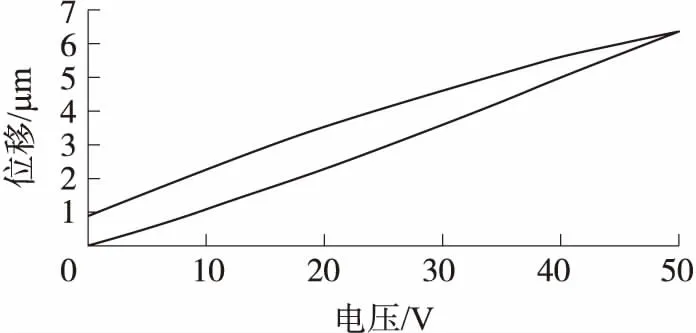
图10 控制前电压-位移曲线

5.2 位移跟踪控制实验

采用前馈逆补偿控制与自适应滑模直接控制分别对同一组频率不同的正弦信号进行跟踪,将得到的实验数据进行采集和处理,得到图12。图中上方的点画线为复合控制下的跟踪曲线,实线为直接控制下的跟踪曲线,离散点为期望位移点。图12下方曲线为两种控制下的误差对比,其中实线为直接控制下的跟踪误差,点画线为前馈逆补偿控制下的跟踪误差。

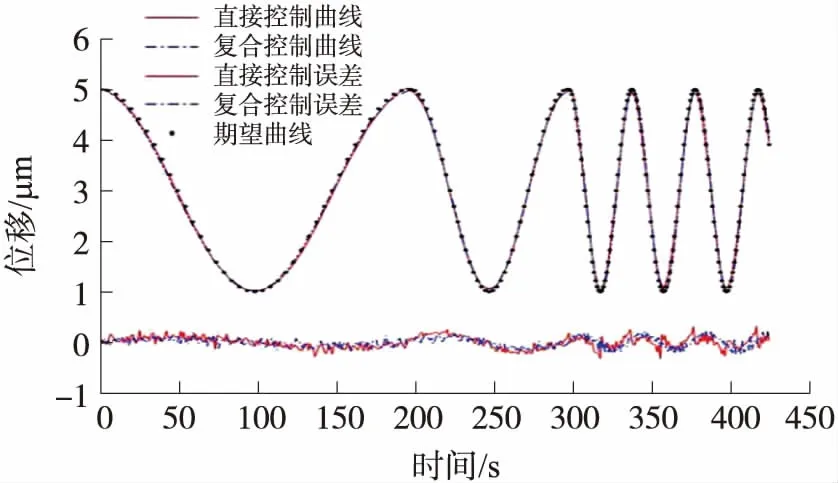
图12 两种控制的时间-位移曲线及其误差

与直接控制相比,前馈逆补偿控制下位移跟踪的输出绝对误差由0.37 μm下降为0.27 μm,下降了27%,平均绝对误差由0.095 μm下降为0.078 μm,下降了17.9%,由此表明逆补偿控制比直接控制更加平稳。

6 结论

本文利用多项式逼近Duhem模型中的未知分段函数f(·)和g(·),利用递推最小二乘法对Duhem模型中的未知参数进行辨识,并根据辨识结果求取逆模型。并采用前馈逆补偿控制进行压电陶瓷的迟滞补偿实验。实验结果表明,前馈逆补偿控制下压电陶瓷的位移迟滞量减小了96.1%,有效的减弱了迟滞,与直接控制相比,前馈逆补偿控制下位移跟踪的输出最大绝对误差由0.37 μm下降为0.27 μm,下降了27.0%,平均绝对误差由0.095 μm下降为0.078 μm,下降了17.9%。前馈逆补偿控制下误差更为平稳,具有更好的鲁棒性和跟踪精度。