外电场作用下MoS2的分子结构和电子光谱*

2019-09-21杜建宾冯志芳张倩韩丽君唐延林李奇峰

物理学报 2019年17期

关键词：基态分子结构电荷

杜建宾冯志芳张倩韩丽君唐延林李奇峰

1) (天津大学精密仪器与光电子工程学院, 天津 300072)

2) (廊坊师范学院理学院, 廊坊 065000)

3) (贵州大学物理学院, 贵阳 550025)

1 引言

近年来, 新型二维纳米材料以其独特的物理化学性质而成为研究的热点.MoS2作为典型过渡金属硫化物[1], 有着与石墨烯类似的二维层状结构,是一种天然的半导体材料, 具有良好的物理化学稳定性, 因此被广泛用于场效应晶体管[2]、光电探测器[3]、电化学储锂[4]和固体润滑剂[5]等领域.另外,由于MoS2具有特殊的二维纳米结构, 它也成为海水脱盐[6,7]、重金属离子液相分离[8,9]和气体小分子过滤[10,11]等的优良材料, 因此在水净化和环保等领域也有着广泛的应用前景.

把分子置于强外电场中, 会出现一些新的物理化学现象, 例如化学键碎裂、新激发态产生、新自由基出现[12,13]以及分子振动斯塔克效应等[12,14-18].李世雄等[19]研究了ZnSe分子的外场效应, 结果显示外场对分子结构有明显的影响; 谢安东等[18,20]对自辐射场下UO3分子的光谱进行了讨论, 证明自辐射场对分子能级有强烈影响; 王藩侯等[13]发现了SnSe的能级和光谱等对外电场有强依赖性;Liu等[21]对5种不同形式的双层MoS2的带隙受外加电场的影响进行了仿真研究.目前, MoS2分子结构和光谱的外场效应研究还未见报道.本文采用密度泛函理论 (density functional theory, DFT)的B3LYP泛函[22-25], 在Def2-TZVP[26,27]基组水平上对MoS2分子的基态几何结构进行了优化, 然后在同样基组水平上采用含时密度泛函(timedependent density functional theory, TD-DFT)[19]方法对MoS2分子的紫外-可见(UV-Vis)光谱在外电场中的变化进行了研究.

2 理论和计算方法

当分子置于外电场中时, 体系的哈密顿量H[28]为

其中,H0为无电场时体系的哈密顿量,Hint是外电场F对分子体系产生微扰的哈密顿量.Hint在偶极近似时表示为

其中µ为分子体系的电偶极矩.

忽略极化率在强场中的非线性效应, 由Grozema等提出的模型[29]可得

其中 Δα为极化率的变化量, Δµ为电偶极矩变化量;Eexc,Eexc(0) 分别为有无电场时的激发能.振子强度f1u为[28,30]

其中,gl等于1, 为加权因子;σ表示能量, 单位为cm-1; 线强度S为原子单位 (e2a02).本文是在Grimme的半经验方法基础上, 把微扰项Hint加入到体系的哈密顿量H0中[20], 并采用TD-DFT[19]来精确计算激发能.

图1为MoS2分子的结构, 本文是在x轴方向上添加上一系列0-0.1 a.u.(0-5.1423 × 1010V/m)的外电场, 也就是把微扰项Hint添加到Gaussian程序的哈密顿量中, 然后采用B3LYP/Def2-TZVP方法, 优化了MoS2分子基态几何结构, 得到了分子密立根电荷分布、总能量和偶极矩, 最后采用TD-DFT方法研究了分子前10个激发态的波长和摩尔吸收系数在外电场中的变化.全部计算由Gaussian09软件包完成.

3 不同外电场下MoS2的分子结构

优化无外电场作用时MoS2分子基态几何结构, 得其电子态为3B1, 分子点群为C2v, Mo-S键长为0.212 nm, S-Mo-S的键角为114°, 红外最强吸收峰出现在546.5 cm-1, 由Mo-S键的伸缩振动产生, 这与实验值535.7 cm-1非常接近[24], 也与其他的计算结果相一致[24,26,31,32], 这说明本文的理论模型和方法是可靠的.

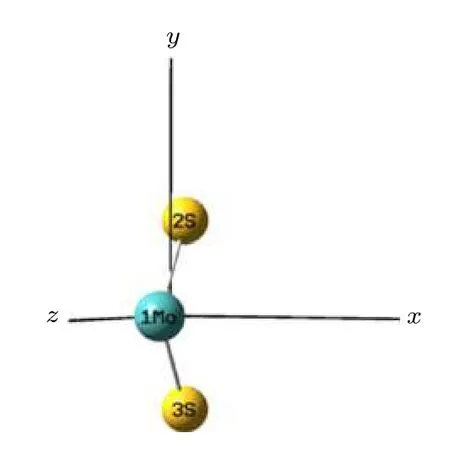
图1 MoS2的分子结构Fig.1.Structure of the MoS2 molecule.

优化不同外电场作用下MoS2分子的基态几何结构, 得到密立根电荷如表1所列.MoS2中S的电负性较强, 无外电场时, Mo的电荷为0.782 a.u.,S的电荷为-0.391 a.u., Mo和S之间的电子云偏向S, 如图2所示; 但随着外电场的增强, 电荷受到的外电场作用越明显, 因此电荷进行了重新分配,即电子发生了整体转移: Mo和S之间的电子云从无外电场时偏向S逐渐向Mo偏移, 伴随原子间着电子云的偏移, 各原子带电量也随之改变, 当外电场增大到0.1 a.u.时, Mo和S的电性也发生了改变, Mo带电荷为-0.069 a.u., S带电荷为0.034 a.u..从图2中可以清晰地看到从无外电场时, 分子的电子云明显偏向S原子; 外电场增大到0.1 a.u., 电子云则主要分布在Mo原子周围, 整个过程中MoS2带电总量始终为0.

表1 不同电场下原子Mo和S的电荷Q/a.u.Table 1.The charges of Mo and S (unit: a.u.) of the MoS2 molecule under different external electric fields.

MoS2的电偶极矩随着外电场的增强而增大,如图3所示, 这是由于外电场诱导出分子的感生偶极矩[15], 同时伴随着电子云相对分子骨架的移动和分子骨架的变形, 即分子的极化, 两者的叠加导致了分子偶极矩的变化.

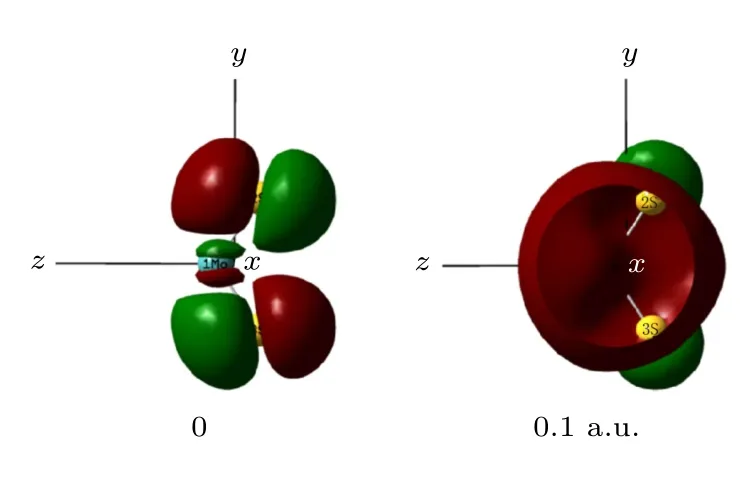
图2 MoS2分子占据轨道侧视图Fig.2.The side view of MoS2 occupied molecular orbital.

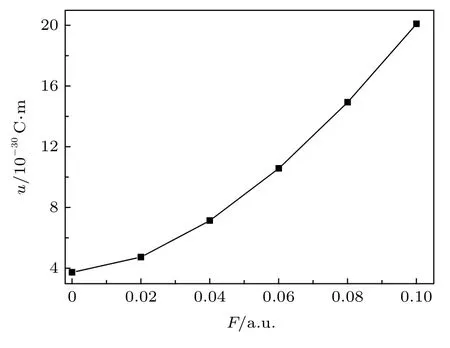
图3 分子电偶极矩u随外电场的变化Fig.3.The relation of dipole moment and electric field intensity of MoS2.

MoS2分子的基态总能量与外电场的关系见图4,F=0 a.u.时, 基态总能量E=-864.7004 a.u.,但当F增大到0.10 a.u.时, 基态总能量E减小为-865.0555 a.u., 且减小的趋势加剧.这是由于内外电场的叠加使得分子几何结构发生了变化: 无外电场时, 分子结构松弛, 分子总能量较大; 但伴随着外电场的增强, 分子结构变得更加紧致、稳固, 分子总能量也随之降低, 计算结果与(1), (2)式也是相符的.

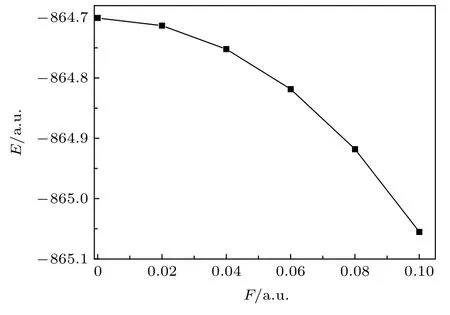
图4 外电场下分子总能量E的变化Fig.4.The relationship between total energy of MoS2 molecule and electric field intensity.

4 不同电场下MoS2分子的紫外-可见吸收光谱

4.1 无外场时MoS2的激发态波长

在优化分子基态几何结构的基础上, 采用TDDFT计算了MoS2分子的前10个激发态, 得到了分子 UV-Vis光谱, 如图5 所示.Jelena Pešić等[33]利用Perkin-Elmer Lambda 4B UV-Vis光谱仪,测量了以N-Methyl-2-pyrrolidone为溶剂的MoS2在350-750 nm波长范围的紫外-可见光谱, 结果显示最强吸收出现在451 nm处.对比文献中的实验数据, 我们的计算与之符合较好, 这也说明了我们的方法是可信的, 并且我们的工作也是对文献很好的补充.

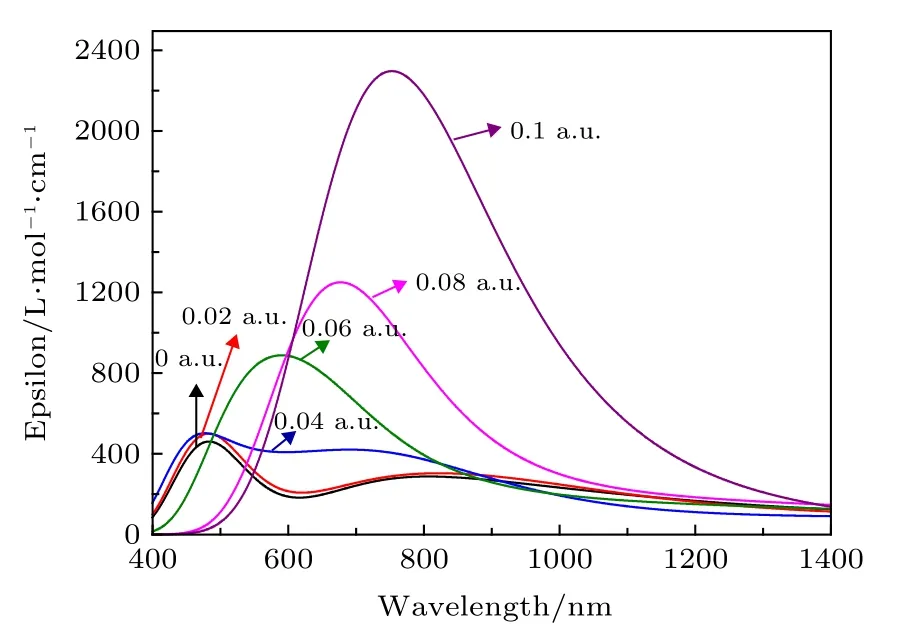
图5 不同外电场下的MoS2分子UV-Vis吸收光谱(Epsilon: 摩尔吸收系数)Fig.5.UV-Vis absorption spectra of MoS2 molecule under different external electric fields (Epsilon: molar absorption coefficient).

4.2 外电场对激发态波长和摩尔吸收系数的影响

在优化的MoS2分子基态几何结构的基础上,采用TD-DFT方法计算了了0-0.10 a.u.的外电场对分子前10个激发态的UV-Vis光谱产生的影响, 如图5所示.可以看出, 当外电场较弱时, 谱峰的波长变化并不明显, 但随着外电场的增强, 吸收峰显著红移, 当外电场增大到0.1 a.u.时, 最强吸收峰波长红移到753 nm, 相比无电场时的吸收峰向长波方向移动了270 nm, 红移非常明显, 这是由于当外电场较弱时, 分子中的电子云主要集中在Mo和S的周围, 如图6占据轨道所示; 但随着外电场的增强, Mo和S周围的电子云沿电场方向发生了整体转移, 这使得Mo和S之间的电子云密度变小, Mo和S之间的相互作用随之变弱, 外层电子更易跃迁到高能级, 也就是跃迁时所需的能量减小, 吸收峰波长变长, 即吸收峰红移.当外电场增大到0.1 a.u., 分子占据轨道的电子云整体转移非常显著, 因此, 此时的红移也就相当明显了.

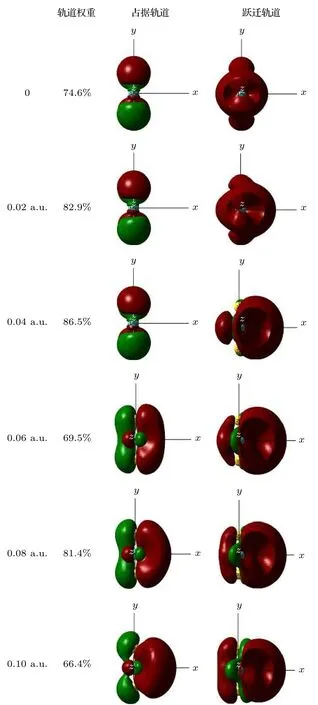
图6 不同外电场下MoS2激发态的分子轨道(占据轨道,填充了电子的分子轨道; 跃迁轨道, 分子被激发时, 电子从占据轨道跃迁到的空轨道; 轨道权重, 分子某一激发态, 构成轨道的各个组成部分的贡献, 图中给出的是所占比例最大的部分)Fig.6.Excited state orbital diagram of MoS2 molecule under different external electric fields (occupied orbitals, molecular orbitals filled with electrons; a transition orbital is a vacant orbital that an electron jumps from an occupied orbital to when a molecule is excited; orbital weight, the contribution of each component of an excited state of a molecule to the composition of the orbital, shown in the figure is the one with the largest proportion).

随着外电场的增强和吸收峰的红移, 摩尔吸收系数开始增大, 尤其是当外电场增强到0.1 a.u.时,摩尔吸收系数已经增大到无外电场时的将近5倍,如图5所示.这是由于外电场对分子内电子的整体转移, 使得Mo和S之间的电子云密度变小(如图6占据轨道所示), Mo和S之间的相互作用随之变弱, 外层电子更容易被激发到到高能级, 这也使得跃迁的电子个数增多; 另一方面, 从图6的跃迁轨道变化也可以看出, 随着外电场的增强, MoS2分子跃迁轨道的电子云密度逐渐增加, 也就是跃迁的电子数增多.本文从占据轨道和跃迁轨道两个角度都证明了外电场的增强导致了跃迁的电子个数增多, 因此摩尔吸收系数也随之增大了.

MoS2分子在外电场中, 吸收峰红移、展宽增加, 摩尔系数增大, 尤其外电场为0.08 a.u.时, 其吸收峰基本覆盖了整个可见光波长范围, 这些都可以提高MoS2对可见光的量子吸收效率, 使其更好地利用太阳能.