基于双波长时域合成技术的微波光子波形产生*

麻艳娜 王文睿 宋开臣 于晋龙 马闯 张华芳

1) (浙江大学生物医学工程与仪器科学学院, 杭州 310027)

2) (浙江大学航空航天学院, 杭州 310027)

3) (天津大学电气自动化与信息工程学院, 天津 300072)

1 引 言

近年来, 多种微波波形, 比如正弦波、方波、三角波和锯齿波, 被广泛应用于医学成像、超宽带有线和无线通信、光学雷达和光学传感等系统中[1-4],其波形质量很大程度上决定了系统的性能.由于采样率的限制, 采用电学方式生成的微波信号具有频率低和带宽窄的缺点.对于要求高频率大带宽的应用场合, 则需要借助光学器件高速、大带宽和抗电磁干扰的优势.

目前, 利用微波光子技术产生高速微波波形是各国人员的研究热点[5-9].其中, 傅里叶光脉冲整形技术[10-13]是常用的方案, 它通过频谱整形技术与频率-时间映射技术的结合来实现, 因此也被称为谱线逐行脉冲整形.而利用Sagnac环的偏振调制也可以产生任意波形微波信号.Liu和Yao[14]利用Sagnac环路内的偏振调制器结构生成三角波、锯齿波和方波波形.Gao等[15]通过环路相位调制器控制信号的强度和相位, 并引入色散补偿, 实现重复频率可调谐的三角波和方波信号.

此外, 通过控制光电调制的调制参数, 也可以实现正弦微波信号到方波和三角波等信号的转变[16-18].张华芳等[19]利用偏振延时干涉技术, 通过调节调制器调制参数和和差分延时线的延时量,得到了5 GHz的方波和三角波输出.Jiang等[20,21]采用时域叠加的方式, 通过调节微波波形谱线间相位关系, 实现了方波、三角波和锯齿波信号输出.Chen等[22]通过集成的偏振复用双驱动马赫-曾德尔调制方案, 避免了大调制系数和光滤波结构, 实现了5 GHz重复频率的全占空比的三角波输出.Li等[23]采用正弦信号驱动的双平行马赫-曾德尔调制器(MZM)和带阻滤波器, 不需要特定的调制系数, 即可实现全占空比的倍频三角波输出.Li等[24]通过双偏振正交相移键控调制器方案, 通过改变X轴相移键控的偏置和调节偏振控制器, 产生了3和6 GHz的三角波和方波波形.

本文提出了一种可调谐的微波多波形产生方法, 通过双波长时域合成技术, 得到与调制正弦波信号同频的方波、三角波和锯齿波信号.本文在理论分析微波多波形产生原理的基础上, 实验生成了2.5和5.0 GHz重复频率的方波、锯齿波和三角波波形.在调制器工作带宽内, 可以方便地实现输出波形重复频率的可调谐, 为任意波形的微波信号产生提供了一种有效的解决方案.因此, 该方案具有良好的应用前景.

2 理论分析

微波波形发生器的原理图如图1.两个单驱动MZM分别偏置在线性工作点和最低功率点位置,当不同波长的两束光波在时域叠加合成时, 可以产生不同的微波波形输出.因此通过调节调制器的偏置电压以及调制深度, 可以实现调制光信号相位和幅度的控制, 最终实现光子微波波形产生.

图1 基于双波长时域合成技术的微波波形发生器原理图, 图中LD为激光器, WDM为波分复用器, PC为偏振控制器, OC为3 dB光耦合器, MZM为马赫-曾德尔调制器,ODL为光延时线, AMP为微波放大器Fig.1.Schematic diagram of the proposed microwave waveform generator based on dual-wavelength time domain synthesis technology.LD, laser diode; WDM, wavelength division multiplexer; PC, polarization controller; OC, 3 dB optical coupler; MZM, Mach-Zehnder modulator; ODL, optical delay line; AMP, amplifier.

假设MZM的微波调制输入为[17-19]

其中Vm为调制幅度,ωm为微波信号的角频率.若光载波的角频率为ω0, 则MZM的输出光场可被近似描述为

其中E0为输出光场幅度,φ=πVbias/Vπ为直流偏置电压Vbias决定的相位偏移,Vπ为调制器半波电压.

将(2)式进行Jacobi Anger扩展, 可得到,

其中Jn为第一类n阶的贝塞尔函数;β为MZM的调制系数, 定义式为β=πVm/Vπ.根据贝塞尔函数的特点, 高阶分量可以忽略不计, (3)式可以只用前三阶频率分量近似表述为

当MZM的电压偏置固定于线性工作点, 即φ=π/2时, MZM的输出光场可被简化为

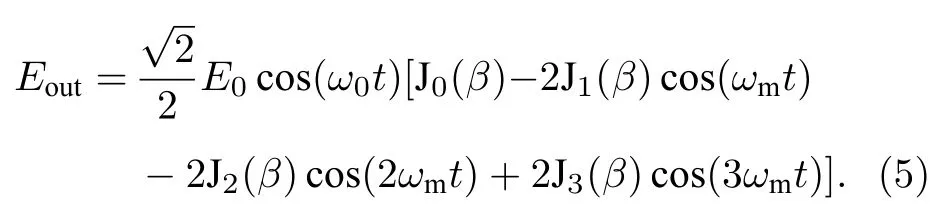
该调制光信号输入到光电探测器后, 由(2)式可得,检测到的微波信号为

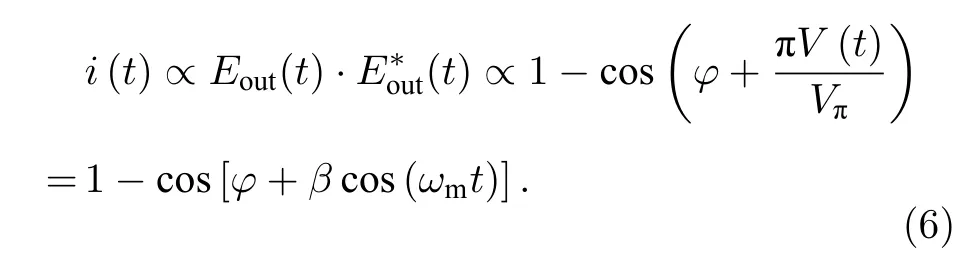
通过Jacobi Anger扩展, 可将MZM的输出经过PD进行光电转换后的微波信号表述为

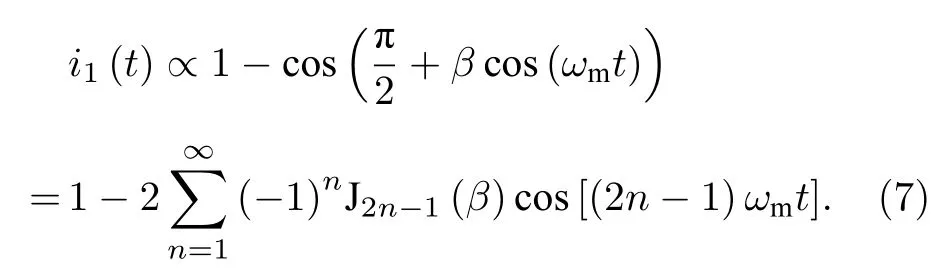
而当MZM的电压偏置为最低功率点时, 将φ=0代入(4)式, 同样可以得到MZM的输出经过PD进行光电转换后的微波信号:

因此, 当MZM工作在线性工作点时, 产生的微波波形只具有奇数阶频率, 而工作在最低功率点时,则只具有偶数阶频率.

2.1 方波波形产生

通常情况下, 归一化方波的傅里叶级数展开可表示为

对比(9)式和(7)式的前三阶频率分量, 得出实现方波输出需要满足以下条件:

因此调制系数β被设定为2.30, 此时产生的微波信号的前三阶分量可被描述为

根据(9)式和(11)式, 可以得到图2所示的仿真结果, 其中虚线表示DC=0时理想的方波波形输出, 实线表示β=2.30 时仅包含前三阶分量的方波波形, 较好地近似了方波波形输出.

图2 β=2.30 时生成的三阶方波(实线)与理想方波(虚线)的波形图Fig.2.Comparison of ideal square waveform (dotted line)and three-order square waveform with β of 2.3 (solid line).

2.2 锯齿波产生

对于锯齿波形, 其傅里叶级数展开可表示为

因此, 锯齿波波形的一阶和三阶频率分量与上述方波波形相同, 可以通过同样的方式获取.而波形的二阶频率分量则通过偏置在最低功率点的MZM2产生.因此, 结合两束光信号即可获得需要的锯齿波波形.MZM1的调制深度仍然设置为2.30, 假设MZM2的调制深度为β2, 忽略3阶以上的频率分量, 则产生的微波信号的交流分量可被描述为

其中θ为两束光信号之间的相对传输延时导致的相位误差, 通过光可调延时线进行调节.为了获取锯齿波波形的三阶近似描述, 要求θ为 π /2 , 且其中θ可通过光可调延时线进行调节, 二阶分量的幅值可通过两束光载波之间的光功率比或者MZM2的调制深度进行调节.而反向对称的锯齿波波形产生则通过调节θ至 3 π/2 , 或者设置MZM2的偏置点至最大值来实现.

根据(12)式和(13)式, 可以得到图3所示的仿真结果, 其中虚线表示DC=0时理想的锯齿波波形输出, 实线表示包含仅前三阶分量的锯齿波波形, 较好地近似了锯齿波波形输出.

2.3 三角波波形产生

归一化三角波的傅里叶级数展开可被表示为

同样将(14)式和(7)式的前三阶频率分量进行对比, 为了满足谐波幅值之间的关系, 要求:

图3 三阶锯齿波(实线)与理想锯齿波(虚线)的波形图Fig.3.Comparison of ideal sawtooth waveform (dotted line and three-order sawtooth waveform (solid line).

因此调制系数β被设置为1.51, 则(7)式中的交流分量可以被改写为

然而一阶和三阶分量之间还存在附加的π相移.为了满足该相位关系, 三角波的产生需要将双波长的光载波与1/4周期时间延迟相结合.假设两个信号具有同样的调制深度和相同的光场幅度, 则结合的信号可被描述为

根据(14)式和(17)式, 可以得到图4所示的仿真结果, 其中虚线表示DC=0时理想的三角波波形输出, 实线为β=1.51 时仅包含前三阶分量的三角波波形, 较好地近似了三角波波形输出.

图1所示的基于双波长时域合成技术的微波光子波形产生方案中生成的方波、锯齿波和三角波波形与理想波形的前三阶分量一致, 仅在高阶分量的系数上存在差异.若仅考虑波形前三阶, 如图2-图4所示, 可实现波形的近似输出.而该方案产生的波形除了含有前三阶分量, 还存在高阶分量, 因此生成的波形相比于上述仿真更接近理想值.波形的各阶分量与理想值的误差通过后续的实验测量进行分析和讨论.

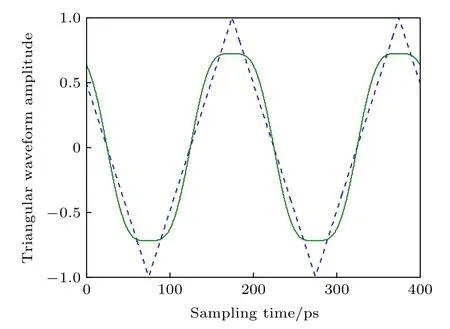
图4 β=1.51 时生成的三角波(实线)与理想三角波(虚线)的波形图Fig.4.Comparison of ideal triangle waveform (dotted line)and three-order triangle waveform with β of 1.511 (solid line).

3 实验与结果分析

图1为基于双波长时域合成技术的微波波形发生器实验装置图.两个分布反馈激光器(LD1和LD2)分别产生中心波长为 1551.2 nm (λ1)和1549.6 nm (λ2)的直流光信号.两路光信号的频率间隔约为200 GHz, 远高于产生的微波波形的频率和光电探测器的带宽, 从而保证激光器的拍噪声不会对最终的波形造成影响.其中, LD2的输出被3 dB光耦合器2均分为2路, 一路与LD1的输出经由3 dB光耦合器1合路后进入马赫-曾德尔型的 LiNbO3光强度调制器 MZM1(Optilab, IM-1550-12), 另一路则进入另一个马赫-曾德尔型的LiNbO3光强度调制器MZM2(Optilab, IM-1550-12).其中, MZM1的偏压固定在线性工作点上, 而MZM2的偏压固定在最低功率点上.两个强度调制器由同一个微波信号源产生的正弦信号驱动, 驱动功率通过调节可调微波放大器(JDSU, H301)的增益进行调节.偏振控制器PC1, PC2, PC3通过调节MZM输入光信号的偏振态, 调节调制器对相应波长信号的插损, 最终实现调整各路调制光信号之间的相对强度的作用.在MZM1的输出端, 通过波分复用器将λ1和λ2两个波长的光分开, 可调光延时线ODL (OZ, ODL-100)则用于调节二者的相对时延.

通过调节调制器的驱动电压, 可以得到需要的方波输出.而通过将两个波长的光通过3 dB光耦合器耦合, 并调节ODL引入的相对延时量, 则可以得到三角波输出.而将λ1波长的光与MZM2输出的λ2波长的光经过光耦合器4耦合, 并调节驱动电压和相对延时量, 则可以得到锯齿波输出.系统的输出端由光电示波器(Agilent, 86100A)观测输出波形.同时由一个3 dB带宽为20 GHz的光电探测器(Optilab, PD-20)将该光信号转换至电域, 由电谱仪(Agilent, 8564E)观测产生的微波信号频谱.

在实验过程中, 首先将微波源输出频率设置为2.5 GHz.调节MZM1的驱动功率, 当驱动功率为19 dBm时, 在示波器可以观测到如图5(a)和图5(b)所示的方波波形.图5(c)为该方波对应的电谱图, 可以看出电谱中1阶分量(2.5 GHz)与3阶分量之间的功率差为9.7 dB, 与理想方波波形的频谱特性基本符合, 5阶分量与理想值相差12.7 dB.此外, 电谱中2阶分量比1阶分量低36.8 dB, 4阶分量接近电谱底噪, 偶数阶分量得到了很好的抑制.

而后保持MZM1的参数不变, 将MZM2的驱动电压功率设置为16.8 dBm, 此时MZM2的输出端可以得到如图6(a)所示的倍频信号, 该倍频信号的电谱图如图6(b)所示.由于MZM2工作在调制曲线的最低点, 奇数阶频率分量被有效抑制, 偶数阶分量, 尤其是5 GHz倍频分量得到增强.

进一步将MZM1的λ1波长信号和MZM2的λ2信号耦合, 并调节MZM2调制深度以调整两路信号的相对强度关系, 可以得到如图7所示的锯齿波波形, 图7(b)为对应的锯齿波电谱图.电谱中1阶分量与2阶分量之间的功率差为6.0 dB, 与3阶分量之间的功率差为9.7 dB, 与理想锯齿波波形的频谱特性基本符合.此外, 4阶分量与理想值相差3.8 dB, 5阶段分量与理想值相差8.4 dB.因此生成的锯齿波信号与理想值符合较好.

此时, 进一步调节光延时线, 经过大约200 ps(π相位)后可以得到如图8所示的反向对称锯齿波波形, 各阶电谱分量与图7基本一致.

然后降低MZM1的驱动功率至15.5 dBm, 此时调节延时线的延时量, 并将两路波长强度调整到近似一致.在耦合器3输出得到如图9所示的三角波波形图.图9(b)为该三角波对应的电谱图, 可以看出电谱中1阶分量与3阶分量之间的功率差为19.3 dB, 与理想三角波波形的频率特性基本符合,而5阶分量比理想值相差5.0 dB.此外, 电谱中2阶分量比1阶分量低35.7 dB, 4阶分量接近电谱底噪, 偶数阶分量得到了很好的抑制.

图5 2.5 GHz重复频率的方波信号 (a), (b)时域波形图; (c)频谱图Fig.5.(a), (b) Generated square waveform with a repetition rate of 2.5 GHz, and (c) its spectrum.

图6 MZM2的输出端的倍频信号 (a) 时域波形图; (b) 频谱图Fig.6.(a) Generated double-frequency waveform and (b) its spectrum in output port of MZM2.

图7 2.5 GHz重复频率的锯齿波信号 (a) 时域波形图; (b) 频谱图Fig.7.(a) Generated sawtooth waveform with a repetition rate of 2.5 GHz, and (b) its spectrum.

图8 2.5 GHz重复频率的反向对称锯齿波信号 (a)时域波形图; (b)频谱图Fig.8.(a) Generated reverse sawtooth waveform with a repetition rate of 2.5 GHz, and (b) its spectrum.

图9 2.5 GHz重复频率的三角波信号 (a)时域波形图; (b)频谱图Fig.9.(a) Generated triangular waveform with a repetition rate of 2.5 GHz, and (b) its spectrum.

图10 5 GHz重复频率的(a)方波信号, (b)三角波信号, (c)三角波信号时域波形图Fig.10.Generated (a) square waveform, (b) sawtooth waveform, (c) triangular waveform with a repetition rate of 5 GHz.

此外, 该微波光子波形产生方案还具有可调谐性, 即可以通过改变微波源的频率灵活地控制产生微波波形的频率.在实验中, 将微波源的频率设置为5 GHz, 采用上述方式, 通过调节调制器的驱动电压、两路信号的相对强度关系和延时线的相对延时量, 得到重复频率为5 GHz的方波、锯齿波和三角波波形 (见图10).

上述实验中波形的产生主要通过信号的时域叠加, 不需要复杂的倍频或滤波技术, 即可直观且方便地实现高频方波、锯齿波和三角波输出, 具有良好的实用性和重要性.通过改变微波源的调制频率即可以实现上述微波波形的重复频率可调谐.在实际测试中, 该方案的操作带宽仅由所使用的MZM调制器和光电探测器的带宽决定.

4 结 论

本文提出了一种基于双波长时域合成技术的微波光子波形产生方案, 首先分析了该方案的理论模型, 而后搭建实验, 通过对系统中MZM调制参数和延时线相对延时量的调节, 实现了2.5 GHz和5 GHz的方波、锯齿波和三角波波形输出.方案中波形的产生均通过信号的时域合成直接完成, 不需要考虑谐波分量之间的相位和幅度关系, 也不需要复杂的倍频过程, 因此可以更直观、更方便地生成所需的微波波形.而产生的微波波形的重复频率主要受到调制器和光电探测器带宽的限制, 因此采用更高带宽的器件可以产生更高重复频率的多波形信号.基于双波长时域合成技术的微波光子波形产生方案具有结构简单、成本较低、操作带宽大和频率可调谐的优点.