读懂教材本旨，巧用数形结合，拓展数学应用

张新民

摘 要 數学教材是教师进行教学活动的主要依据，也是学生进行学习活动的主要基础，它是师生完成教与学双边活动必不可少的媒介。教学中，教师根据教材所提供的信息资源和蕴含的数学思想引导学生探索数学规律，掌握数学技能，培养数学素养。读懂教材就是把教材转化为学生有效的学习过程。

关键词 读懂教材;数形结合;数学应用

中图分类号：G622         文献标识码：A       文章编号：1002-7661（2019）10-0189-01

本文试图通过列举北师大三年级数学教材上册中的典型案例，探索教师在具体的教学组织中如何读懂教材本旨，巧用数形结合，拓展数学应用。

一、说一说，再列式算一算

这是教材中最常见的一种呈现方式，也是数形结合最常见的一种表现形式。如第一单元《混合运算》“小熊购物”中出现的场景在教材中就频繁出现。

就教材的本意而言，其所谓的“说一说”，说的就是“形”所寓含的数学信息;其所谓的“再列式算一算”，算的就是数学信息中所寓含的算理。对于第一类型的题，我在教学中常用给图形分类的方法，及将整齐排列而有规则的部分归为一类，再将零乱的不规则的部分归为一类。这样在已有的图示基础上，在辅之以新的“形”，是原来的图示更加富有条理，其算理也愈加清晰。不用老师繁琐的讲解，学生一眼就能够看出将两类相加求和的算理。在教学中，教师就要吃透教材的这个编排意图。首先让学生观察，说一说图中的内容，做到不重复，不遗漏，有条理。然后根据教材的特定问题，引导学生找到解决问题的方法。最后，也是最重要的一点，就是把图示和问题结合起来，不断去创造数形结合的新架构。

二、分类讨论问题

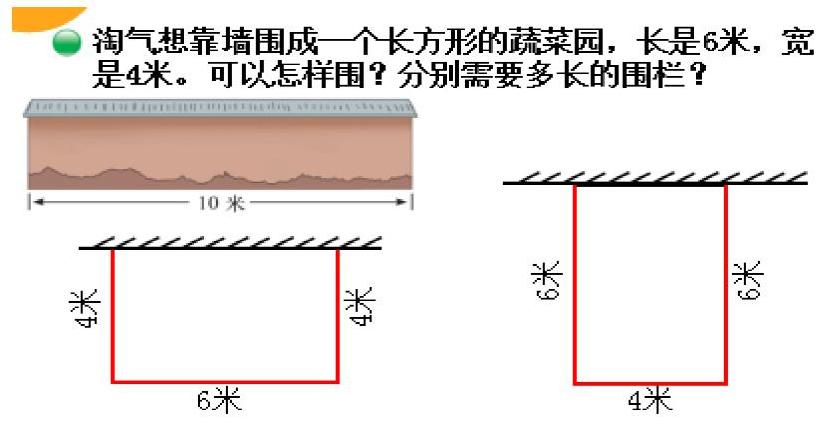
课程标准在总目标中要求学生能够有条理地思考，这种有条理性的思考就是一种有顺序的、有层次的、全面的、有逻辑性的思考，分类讨论就是具有这些特性的思考方法。比如在《长方形的周长》单元中教材出现了这样的练习题型：

很显然，教材的本旨不仅在于长方形周长计算方法的熟练掌握，而是更加注重结合生活实际的应用，以及根据特定的情景能够分类解决问题。在实际教学中，我是逐步来实现教材意图的。首先允许学生犯错，在错误中恰恰能暴露出学习当中被掩盖的失误和忽视的要点。有一部分学生往往不加深究，直接套用长方形的计算公式进行计算。当这样的结果出来后，老师并不急于作出判断，而是不失时机地教给学生分组讨论。有些学生就会发现靠墙的一边不需要用围栏。这个发现一经揭出，然后老师鼓励学生用画图的方法帮助学生理解和计算。很快学生得出了两种不同的结果，那么到底是哪一种准确呢？老师把问题梳理出来后又一次抛给了学生。然后公说公有理，婆说婆有理，争得不亦乐乎！最后分类讨论的方法水到渠成一般就形成了。在解决这样较复杂的问题过程中，我始终紧紧抓住数形结合不放松。先是依赖纯粹的“数”套公式解决;此路不通，再联系“形”;偏而不全，再将“数”、“形”分类结合。在教学中教师引导学生尝试画一画，表示出题目的意思。两种图示、两种计算，这样就进一步加深了学生对长方形周长计算方法的理解。可见数形结合有效地防止了学生的生搬硬套，打开了学生的解题思路，由不会解答到用多种方法解答，学生的知识更加丰富了，兴趣也变得更加浓厚了。

三、画线段图帮助分析数量关系

在第三单元“加与减”有关里程表一部分的内容，教材不仅形象地展示了实况比例图，还列出表格给出了相关里程的具体数量。可见教材无处不将数形结合展示得极其充分。但在教学中，如果只是看到这一点，没有真正明白教材的更深的意图，教学的效果将大打折扣。

我在教学中，不仅充分利用了教材的这一编排意图，采用交互式电子白板，在比例图中直观地标示出数量之间的关系，然后让学生直接按照数形结合的思想，将图表结合，求出答案。教学至此，似乎完成了教学目的。但是为了今后的学习深度的拓展，以及灵活应变各种数学生活场景，我在此基础了，进一步引入线段图的形式，引导学生适度抽象地表达数量关系。教师引导学生用线段图的形式表示题目中的数量关系，更直观，形象，具体。在整个小学数学学习阶段，可以说，借助线段图准确找出数量间的对应关系，是数形结合思想最常用，最有效的的体现。比如在后面学习难度较大的“求比一个数的几倍还多几（少几）”的应用题，线段图更是如鱼得水。

在教学中渗透数形结合的思想，可把抽象的数学概念直观化，帮助学生形成概念;可使计算中的算式形象化，帮助学生在理解算理的基础上把握算法;可将复杂问题简单化，在解决问题的过程中，提高学生的思维能力和数学素养。总之，适时地将教材中所渗透的数形结合的思想挖掘出来，并进一步运用数形结合的教学方法，确实可以达到事半功倍的效果。

参考文献：

[1]刘昆杰.渗透数形结合思想无痕拓展数学思维[J].内蒙古教育，2018（08）：70-71.