亲近数据感悟随机
——《可能性》教学实践与思考(一)
2019-09-20鲍善军
鲍善军
【教学内容】
人教版五年级上册第四单元。
【课前慎思】
21世纪以来,“统计与概率”单独作为一个学习领域进入小学数学课堂,这是一次具有深远意义的里程碑式改革。尤其是新课标的重新修订,新教材对“可能性”教学进行了大幅度的调整。如何重新认识小学阶段“可能性”教学的意义和价值?又如何在具体的教学活动中加以体现?有必要作一些思考与实践。
“通过实例感受简单的随机现象,能列出简单随机现象中所有可能发生的结果;通过试验、游戏等活动感受随机现象结果发生的可能性是有大小的,能对一些简单随机现象发生的可能性大小作出定性描述。”从以上表述中,我们至少可以这样理解:一是明确所涉及的随机事件仅限于简单随机事件,即所有可能发生的结果是有限的,且每个结果发生的可能性是相同的;二是只要求对可能性的大小作出定性描述,而不是进行定量表达。
如何通过“试验、游戏等活动”感受可能性的大小?虽然随机事件的发生不可预知,但存有一定的规律性,通过大量的重复试验收集到足够的数据信息后,可以借助数据分析可能性的大小,而不是急于从定义和假设出发进行概率的计算。就数学思维而言,“可能性”关注的是现实世界中的随机事件,随机思维与确定性思维迥然有异。统计的核心是数据分析。因而,小学阶段“可能性”的价值就在于通过感受随机现象培养学生的数据分析观念。这与“统计与概率”领域的总体课程目标是完全一致的。
美国华盛顿儿童博物馆的墙上有这样一句格言:我听见了就忘记了,我看见了就记住了,我做过了就理解了。体验了,方才知其所以然。可能性这部分内容看似简单,却是学生第一次接触简单的随机现象。为此,教学中应引导学生在丰富的活动体验中感受随机性,在数据思辨中感悟“可能性”,学会从数据的角度看待可能性大小,知道有些事情需要通过调查去估计或推断,养成用数据分析问题的习惯,从而体会相应的思维方式,积累学习经验。
【课中深思】
一、创设情境,实施任务驱动
师:(出示黑色布袋)袋子里装有若干个红、黄两种颜色的球(除颜色外其他都相同),你有什么办法知道两种颜色的球各有多少个?
生:把袋子里的球全部倒出来数一数就知道了。
师:这个办法很好,不过技术含量太低了。现在规定不能倒出来看,也不能直接打开袋子数。
生:我想知道袋子里红、黄球一共有多少个?
师:一共有5 个。
生:可能是5 个红球,或者5个黄球,也可能是4 红1 黄、3 红2 黄、2 红3 黄、1 红4 黄。
师:你列举了所有可能的情况。那么,袋子里的球会是其中的哪一种呢?生:3 红2 黄。师:确定吗?生:不确定。师:为什么?
生:因为我是乱猜的。
师:如果不乱猜,你们有什么好办法吗?
生:摸一次放回去,再摸一次又放回去,这样可以吗?
师:这个办法可行,每摸完一次放回去,摇一摇后再摸。那么,你准备摸几次?
生:摸5 次。
生:5 次肯定不行。没那么巧每次摸到都是不同的球。
师:你们的意思是摸5 次太少了?那如果多摸几次呢?
生:(不确定)多摸几次,应该可以吧。
师:多摸几次,说不定真可行,那我们试试?
二、动手操作,经历统计过程
师:以小组为单位,进行实验操作。每组一个黑色袋子,里面装有5 个球,球的数量结构包括5红、3 红2 黄、2 红3 黄和1 红4黄四种情况。
出示操作要求:
1.闭着眼睛,每次任意摸出一个球。
2.用打“√”的方法把每次摸到球的颜色记录在表格中,最后统计结果。
3.记录之后,把摸出的球放回袋中,摇一摇后再摸。
4.10 次10 次地摸(最多30次),摸到可以得出结论为止。
(学生操作后,小组反馈形成下表)
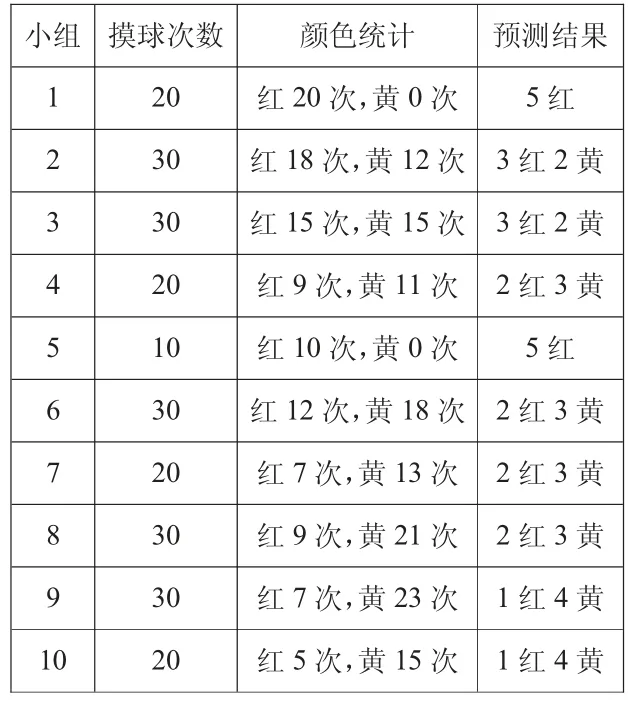
images/BZ_20_265_2210_340_2270.png小组 摸球次数 颜色统计 预测结果1 20 红20 次,黄0 次 5 红2 30 红18 次,黄12 次 3 红2 黄3 30 红15 次,黄15 次 3 红2 黄4 20 红9 次,黄11 次 2 红3 黄5 10 红10 次,黄0 次 5 红6 30 红12 次,黄18 次 2 红3 黄7 20 红7 次,黄13 次 2 红3 黄8 30 红9 次,黄21 次 2 红3 黄9 30 红7 次,黄23 次 1 红4 黄10 20 红5 次,黄15 次 1 红4 黄
三、展开思辨,感悟数据价值
1.同样的数据为什么推测出不同的结论?
师:同学们通过小组操作,预测了袋子里的装球情况。请问,你们是怎样得到结论的?大家是乱猜的吗?
生:我们根据摸球之后记录的数据来猜测结果,但不是乱猜。
师:你说的数据是指什么?
生:就是摸到两种颜色球的次数。
师:也就是说,你们的结论是根据两种颜色的球被摸到的次数推测出来的,对吗?
生:(齐)对。
师:我发现第3 组的数据比较特殊,说说你们是怎样分析的。
生:(3 组)我们组摸到30 次时,红、黄球次数一样,说明袋子里红球和黄球数量相差不大,所以可能是3 红2 黄,也可能是2红3 黄。
师:你的意思是根据摸球得到的同样的数据,推测出了两种不同的结论?还有其他小组也有这样的想法吗?
生:(8 组)我们组摸到红球9次,黄球21 次,黄球明显多于红球,可能是1 红4 黄,也有可能2红3 黄。
师:同学们能根据数据来推测结果,非常好!虽然同样的数据可能推测出不同的结论,但总比乱猜的结论更可靠一些,同意吗?
2. 不同的数据为什么推测出同样的结论?
师:观察统计表,有哪些小组的预测结果是相同的?
生:第1 组和第5 组预测结果都是5 红,第9 组和第10 组都是1 红4 黄,还有第2、3 组是3 红2黄,第4、6、7、8 组是2 红3 黄。
师:我们再来观察,预测结果相同的小组得到的数据相同吗?
生:不同。
师:那么,不同的数据为什么推测出同样的结论?举例说一说。
生:(6 组)我们摸到红球12次,黄球18 次。红球比黄球少,但相差不大,所以推测是2 红3 黄。
生:(8 组)我们摸到红球9次,黄球21 次。红球比黄球少,虽然相差较大,但我们觉得有可能是2 红3 黄。
师:越来越棒了!先根据谁被摸到的次数多,就判断哪种颜色的球多;再看次数相差得大不大,从而推测出红球和黄球各有几个。是这样吗?
生:是的。
师:老师发现,各小组摸的总次数有10 次、20 次,也有30 次。相对而言,摸30 次的小组多一些,你们怎么看?
生:摸30 次,更能确定袋子里的红、黄球数量。
生:摸得次数越多,预测结果的准确性越高。
师:你们的意思是数据越多,结论越准确,是吗?那摸10 次、20次得出的结论就一定不准确吗?
生:那也不一定,得看运气。
生:我认为摸30 次的准确性高于20 次的,摸20 次的准确性高于10 次的。
生:(5 组)我们摸完10 次都是红球,就觉得袋子里可能全是红球。
生:(1 组)我们组也是这么想的,但摸完10 次后感觉不放心,万一有黄球没摸到呢?于是,又摸了10 次,结果还是红球。心想运气不会这么差吧,就不摸了。
师:如果继续摸,摸50 次、100 次,甚至是更多次呢?
生:也不一定,如果运气特别差,还是不能确定的。
师:要完全确定袋子里的装球情况,怎么办?
生:打开看一看。
3.同样的数量结构为什么摸到的结果不一样?
(经统计,第4 组猜错,其他小组正确)
师:这么多小组的预测结果正确,说明了什么?
生:说明我们摸了这么多次还是很有用的。
生:说明不能乱猜,要根据数据来猜。
生:根据数据来推测结果,更准确一些。
师:为你们点赞!我们通过摸球得到的数据非常有价值,它与袋子里红球、黄球的个数确实存在着一定关系。或者说,这些数据是有规律性的。
师:既然数据有规律性,为什么第4 小组预测结果错了?
生:(4 组)我们摸了20 次,红球9 次,黄球11 次,红球少于黄球,我们就猜了2 红3 黄。
师:红球9 次,黄球11 次,你们会怎么猜?
生:我也会猜2 红3 黄。
师:可实际结果是3 红2 黄,这是为什么?
生:因为我们是随意摸的,有可能运气不太好,得到的数据就不准确。
生:说明还是有点不确定。
师:不确定、运气,在数学上叫随机性。第4 组的情况说明数据具有随机性,还有哪里也可以读出数据的随机性?
生:第2 组和第3 组的结果都是3 红2 黄,可他们摸出红球和黄球的次数不一样。
师:是的。像这样,同样3 红2 黄的数量结构摸到的结果却不一样,体现了数据的随机性。如果让你在这些小组的袋子里再摸一次,你可以确定摸到什么颜色的球吗?
生:第1 组和第5 组的袋子确定,其他组不行。
师:在第1 组或第5 组的袋中再摸一次,一定是?不可能是?
生:一定是红球,不可能是黄球。
师:第1 组和第5 组袋中的结果能确定,叫确定事件。确定事件包括一定发生和不可能发生。其他组都无法确定,摸到的可能是红球,也可能是黄球,叫不确定事件。如果老师和你玩一个猜摸球颜色的游戏,你有优先权,你会选哪个小组的袋子?
生:我选只装有5 个红球的袋子,猜红球肯定赢。
师:如果是3 红2 黄的袋子,你会猜什么颜色?为什么?
生:红色。因为红球多,摸到的可能性大。
师:你一定会赢吗?
生:不一定。因为摸到的球具有随机性。
4.不同的数量结构有可能摸到同样的结果吗?
师:如果在3 红2 黄和2 红3 黄的袋中分别摸10 次,你觉得有可能摸到同样的结果吗?
生:有可能。因为两个袋子中红球和黄球数量相差不大,而数据又有随机性。
师:那如果在3 红2 黄和1红4 黄的袋中分别摸10 次呢?
生:看运气,也有可能,但可能性很小。
师:确实是这样。数据既有规律性,也有随机性。我们要相信数据,又不能全信。没有数据,很多事情会变得盲目;但过分依赖数据,有时也会让我们的判断产生偏差。是这样吧?
生:是的。
四、联系生活,提升可能性认识
1. 出示教材第49 页主题图“生活中的数学”,你能用今天学习的知识解释图中的现象吗?
2.日常生活中经常会用到可能性的大小,你能举例说明吗?
五、课堂小结,回顾学习过程
师:通过这节课的学习,你对可能性有了什么新的认识?有什么收获与体会?
【课后研思】
小学生大多是确定性思维,这与我们长期的数学教学有一定的关系。为什么要学习可能性呢?主要是为了培养学生的随机思维,让其学会用概率的眼光去观察丰富多彩的大千世界。
史宁中教授指出:“统计教学很重要的是培养孩子们对于数据的感情。”小学阶段可能性教学更多偏向统计,用数据来推断可能性的大小,核心思想是对不确定事件的关注,让学生体验事件发生的随机性。课堂中设计“暗袋”,学生没法看,只能先估,最后才打开看袋子加以印证。为什么要先估呢?在估的过程中更有利于学生亲近数据,感悟随机,体现数据的价值,培养数据分析观念。
“暗袋”的特点是引导学生用实验所得数据进行分析,进而推测袋中球的数量结构。整堂课围绕“数据”展开思辨:同样的数据为什么推测出不同的结论?不同的数据为什么推测出同样的结论?同样的数量结构为什么摸到的结果不一样?不同的数量结构有可能摸到同样的结果吗?这样的设计实际上是基于新时期学生经验概率的高认知起点,直接跳过了教材的例1 和例2,从例3开始教学,目标定位不是仅停留在概率教学本身,而是引导学生去关注数据,培养数据意识。从课堂效果来看,这样的教学实践是适切而科学的。
所谓“观念”,并不是一种简单的技能,而是需要在亲身经历的过程中培养出来的感觉,它反映的是由一组数据所引发的想法,所推测到的可能结果,自觉地想到运用统计的方法解决有关的问题等等。当然,如果我们在课堂教学价值追求上再高一点,甚至上升到哲学层面。我们怎样用数学的眼光观察这个充满不确定性的客观世界,用数学的思维辩证地看待和思考现实问题。相信,对学生的长远发展是有所帮助的。
当然,本课的设计与实践一定还存在许多不足之处,恳请各位方家批评指正!
