用于绕线机的全数字张力控制系统研究

宋辰亮，余振平，高景衡，曾 胜

(浙江大学化工机械研究所 浙大-集智研发中心，杭州 310027)

0 引言

张力控制技术广泛应用于各种长尺寸材料的收卷、放卷和加工等工艺过程，在这些过程中，材料的张力大小及稳定性是重要的工艺参数。例如在精轧工艺中，精轧张力的精确控制可以降低带钢宽度拉窄所带来的剪切损耗，提高带钢成材率[1]。在纤维复合材料缠绕时，稳定的张力可提高纤维的增强特性[2]。在纺织过程中，纱线张力的大小直接影响织物的质量、性能和加工效率[3]。在卷筒纸印刷工艺中，纸路横向或纵向折皱、套印不准等现象，与张力的控制有关[4]。

绕线机是用于绕制电磁线圈、电动机线圈和精密电阻器等各类线圈产品的专用设备，其张力控制系统是决定产品质量的重要因素。在高品质超细漆包线圈的绕制过程中，绕线速度高，许用张力小，绝缘层不允许出现拉伤、破损等缺陷，且线圈品种繁多结构不一致，这些都对张力控制系统的性能提出了很高的要求[5]。薛秉仁[6]设计的绕线机控制系统中，使用力传感器测量漆包线的张力。温何等[5]给出了一种使用电容式角位移传感器的张力检测方案，经过频率调制和频压转换后输出电压信号。Pan Jun等[7]研究了一种用于漆包线高速绕制的电子张力控制器，使用非接触式光学角度电位器测量张力。王显峰等[8]和徐礼平等[9]都进行了金属丝缠绕实验，张力波动都约为±5%。韩帅[3]进行的纱线绕制实验显示张力最大波动约±1%。这些研究中的张力控制系统都使用模拟信号传感器，本文使用增量式光电编码器作为传感器，研究一种全数字的张力控制系统方案，并进行实验验证。

1 张力控制机械结构及其工作原理

漆包线受张力作用会产生拉伸变形，但其形变太小无法直接测量，因此用摆杆弹簧机构来放大形变。图1是简化的张力控制机械结构：端部带瓷环的直摆杆，可绕O点摆动；弹簧的一端固定，另一端连接到摆杆上；漆包线从线源出发，分别绕过导轮1、放线轮(安装在放线电机的伸出轴上)、导轮2、瓷环和导轮3，最后进入绕线机(绕线电机和绕线骨架等)。其中放线轮外缘开有V型槽，内嵌O型圈，以增大摩擦力。可以看出张力控制机械结构中，张力T、摆杆的摆角θ(摆杆与竖直方向的夹角)、绕线线速度V1(t)和放线线速度V2(t)之间的关系为：

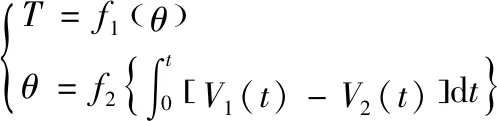
(1)

当放线线速度V2(t)大于绕线线速度时V1(t)时，摆杆顺时针摆动，摆杆的摆角θ变小，张力T变小；反之，摆杆逆时针摆动，摆角θ变大，张力T变大。当放线线速度V2(t)与绕线线速度时V1(t)保持一致时，摆杆就稳定在某一位置，此时的张力T的大小由弹簧拉力唯一决定，而弹簧拉力又由摆角θ决定，因此张力T和摆角θ有一一对应关系。将摆角θ作为控制系统的被控变量，将放线线速度V2(t)作为控制系统的控制量，跟踪绕线线速度V1(t)，就能够实现张力T的控制。

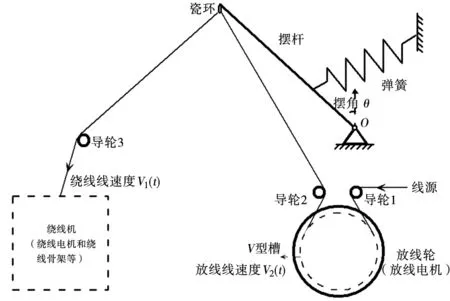
图1 漆包线张力控制机械结构简图

图1所示的张力控制机械结构，是一个质量-弹簧-阻尼机械系统，由于存在多个储能元件但没有特殊的阻尼元件，所以机械结构会呈现出振荡特性。

2 控制系统结构

用增量式光电编码器测量摆杆的摆角，这是一种输出电平脉冲信号的纯数字传感器，信号分辨率和精度较高，更新周期短。

常用的控制电机中，交流伺服电机的响应时间短、加减速快、转速稳定性好，能够较好地保证放线线速度快速、精确、稳定地跟踪绕线线速度。

选用PIC16F1778单片机作为控制器。用输入捕捉模块接收编码器信号，通过计数和相位比较[10]得到摆角θ。用脉宽调制(PWM)模块输出频率可调的脉冲信号驱动交流伺服电机。最高频率可达32MHz的系统时钟保证单片机能够快速实现数字控制规律。将通用收发器模块配置为半(全)双工异步通信系统基于RS485或RS232总线进行通信，通信编程遵循西门子PPI通讯协议，能与S7-200等PPI主机进行通讯。

图2为控制系统方框图，将执行器与张力控制机械结构合称为被控对象。单片机接收编码器输出的摆角测量值信号，将其与设定值比较后得到偏差，经过软件控制规律处理得到转速控制信号并作用于被控对象，实现完整的闭环反馈控制。

综上所述，传感器输出的是代表摆角信息的电平脉冲信号，控制器输出的是代表转速信息的数字脉冲信号，所以系统控制回路中的关键信号都是数字信号。这是一个全数字的控制系统，但是仍旧能用传统的传递函数方法来分析。

图2 控制系统方框图

3 张力控制系统分析

3.1 被控对象特性

为了得到被控对象的传递函数，可在稳态静止条件下，控制器输出一个100r/min的转速阶跃信号，驱动放线电机。测试得到的转速阶跃输入摆角响应曲线如图3所示。图中的曲线在0～3ms内，摆角θ没有改变，这是被控对象的纯滞后。在3～100ms时间范围内，响应曲线为直线与正弦衰减曲线的叠加。根据式(1)，其中直线段应为收放线线速度差随时间累积的体现，正弦衰减曲线应是机械振荡特性的体现。将控制器输出的转速阶跃信号改变为角位移阶跃信号，再次测试得到角位移阶跃摆角响应曲线如图4所示，这是一个典型的二阶欠阻尼系统衰减振荡曲线，且同样存在3ms的纯滞后。

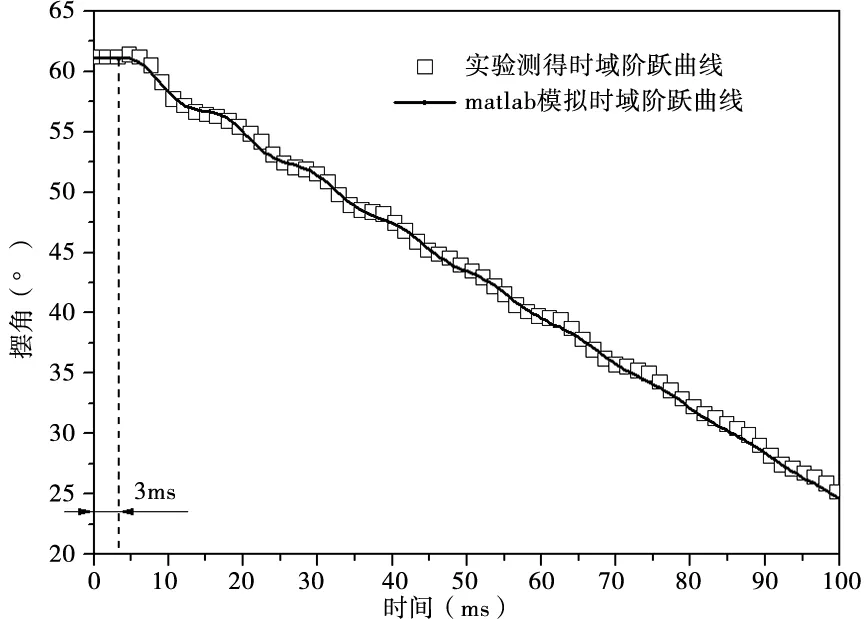
图3 被控对象时域转速阶跃输入摆角响应曲线

图4 被控对象时域角位移阶跃输入摆角响应曲线

根据上述测试结果，可将被控对象特性简化为积分环节、二阶振荡环节和纯滞后环节的叠加。建立式(2)所示的被控对象传递函数，其中XO(s)为输出角度象函数，Vi(s)为输入转速象函数，传递函数的量纲为(°·min)/r。

(2)

式中，K为增益，ω为阻尼自振角频率，a为常数(与阻尼比和ω有关)，τ为纯滞后时间。

式(2)的单位阶跃响应为：

XO(t)=

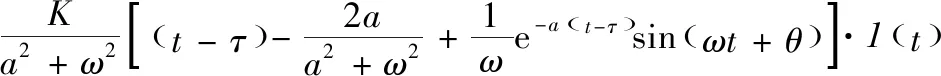
(3)

二阶振荡环节传递函数G(s)及其单位阶跃输入响应曲线的包络线解析式[11]见式(4)。其中ζ为阻尼比，ωn为无阻尼自振角频率。

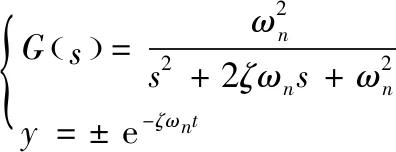
(4)

用式(3)和式(4)对图3和图4进行拟合，得到各参数值，其中τ=0.003s，ɑ=24.2rad/s，ω=534rad/s，K=-1.08e8°/s3。这些参数是以100r/min转速为单位阶跃条件下测得的，而控制器的实际输出单位转速信号为1r/min，因此增益K应该缩小100倍，即为-1.08e6°/s3。由此得到式(5)表示的被控对象传递函数，量纲为(°·min)/r。

(5)

依照式(5)，将其在100倍单位阶跃输入作用下的时域响应曲线绘制在图3中。可以看出，模拟得到曲线与测试得到的曲线趋势一致，振荡波形同步，所以式(5)作为被控对象的传递函数是比较精确的。

3.2 控制参数整定

将数字控制器看成是带有0.5ms纯延时的模拟控制器，控制算法以位置式PID控制规律为核心，如式(6)所示。式(6)中有3个控制参数需要整定，分别是KP，TI和TD。在SIMULINK中建立如图5所示的控制系统模型。模型中的测量反馈是单位反馈，其单位为度(°)；控制器的输出控制信号是转速，转速范围限制在±3000r/min以内；另外，模型中还包含被控对象的传递函数、3.5ms纯延时(被控对象的3ms纯延时加上控制器的0.5ms纯延时)和设定值小幅阶跃等模块。

(6)

参考临界比例度法进行控制参数整定。该方法首先求取在纯比例作用下的闭环系统为等幅振荡过程时的比例系数和振荡周期，然后根据经验公式计算出相应的PID参数[12]。根据以上步骤进行仿真计算，在纯比例控制条件下，当比例系数为48.72时得到了如图6所示的等幅振荡过渡过程曲线，振荡周期为0.0156s。因此控制系统临界比例系数为48.72，临界周期为0.0156s。根据经验公式，当使用PID控制规律时，比例系数KP为临界比例系数的0.6倍，积分时间TI为临界周期的0.5倍，微分时间TD为临界周期的0.125倍，即KP=29.2，TI=0.00778，TD=0.00195。将这组PID参数输入到模型中，同时微分滤波系数N取为10，得到设定值小幅阶跃响应曲线如图7所示，其衰减比近似为4：1，表明参数整定得到的这组PID参数可以作为初始PID参数使用。

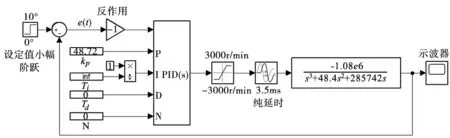
图5 控制系统SIMULINK模型

图7 初始PID参数下设定值小幅阶跃响应曲线

3.3 张力与摆角关系

摆杆的摆角θ是控制系统的被控变量，但是实际上要控制的是漆包线的张力T。由图1张力控制机械结构的工作原理可知，在稳态情况下摆杆的摆角θ与漆包线的张力T有一一对应的关系，具体的数量关系需要在放线电机不转动的情况下使用拉力计进行标定。有两种方案。一种是当弹簧确定时，用拉力计缓慢牵引从导轮3离开的漆包线，同时记录拉力计的示数和控制器测得的摆角θ，建立张力T与摆角θ的对应表格，存储在控制器中，设定张力T时，通过插值查表法得到对应摆角θ；系统运行时，由实时摆角θ查表得到对应张力T。此方案得到的张力T与摆角θ关系见图8。如果实际使用时需要频繁更换弹簧，或者弹簧力会缓慢时变，则有另一种方案。拉力计牵引漆包线至张力设定值位置，然后控制器记录此时的摆杆摆角θ作为当前摆角设定值。实验时采用前一种方案，张力T与摆角θ的转换工作由控制器完成。

4 实验

参照图5中SIMULINK的PID算法，以采样周期0.5ms离散化，编写单片机程序。使用整定得到的初始PID参数KP=29.2，TI=0.00778，TD=0.00195，在实验装置上进行绕线的张力控制实验，测试张力控制系统性能。漆包线线径0.08mm，绕线电机角加速度3000r/(min·s)，圆形绕线骨架的初始直径62mm，张力设定值为54g，对应摆角设定值约为41°。

4.1 瞬态性能测试

当绕线电机突然运转时，图1中的绕线线速度V1(t)开始建立，在控制系统作用下放线线速度V2(t)跟踪绕线线速度V1(t)，使摆杆稳定在摆角设定值位置，同时张力稳定在设定张力值。

初始绕线直径约为62mm，实验得到绕线电机突然启动条件下的瞬态响应曲线如图9所示，可以看出，绕线电机启动0.14s以后，在控制系统的作用下，摆杆摆角θ到达设定值附近，至0.83s时刻绕线电机达到目标绕线转速2800r/min，此时绕线线速度约9m/s；在0.14～0.83s时间段内，响应曲线存在较小的超调和振荡，最大偏差为3.2°，对应张力超调约2.8%；绕线电机转速稳定后约30ms，摆角θ就迅速稳定到摆角设定值。整个瞬态过程超调小、调整时间短、动态性能较好。

4.2 稳态性能测试

使绕线电机以固定转速2500r/min稳定运行，初始绕线直径约为75mm，绕线过程中，绕线直径会缓慢增大，平均绕线线速度大于10m/s。得到如图10所示的张力随时间变化曲线。图中，平均张力为54.04g，最大张力54.37g，最小张力53.70g，即最大张力偏差为0.34g，张力波动(最大偏差除以平均值)为±0.63%，优于文献[3,8-9]中给出的稳态张力波动值±1%，±5%，±5%。

4.3扰动条件下性能测试

设定绕线电机基准转速为2500r/min，并给予绕线电机幅值250r/min，频率1Hz的转速扰动，初始绕线直径约为78mm，最大绕线线速度达到11.5m/s。得到如图11所示的张力随时间变化曲线。图中，平均张力为54.05g，最大张力54.54g，最小张力53.53g，即最大张力偏差为0.52g，张力波动为±0.96%，与文献[3]给出的稳态波动值相当。

图8 张力T与摆角θ对应关系

图9 绕线电机突然启动条件下摆角时间曲线

图10 转速固定条件下张力时间曲线

图11 转速扰动条件下张力时间曲线

4.4 关于控制参数

上述实验是在整定参数KP=29.2，TI=0.00778，TD=0.00195时进行的，取得了较好的运行效果。实验发现，在这组参数附近，改变参数值也能得到类似的控制效果，这个范围是KP=20～45，TI=0.006～0.016，TD=0.001～0.004。需要指出的是，3个参数的取值，不能同时取范围的极值。

5 结论

本文研究了一种全数字的张力控制系统，控制回路中的关键信号都是数字信号，由于不需要对数字信号进行滤波和模数、数模转换等处理，因此控制系统十分精简，容易进行批量化生产并且可靠性较高。在实验装置上进行了线径0.08mm漆包线的绕线张力控制实验，最高绕线线速度达到11.5m/s，可以通过增大放线轮直径进一步提高绕线线速度。瞬态性能测试结果表明张力控制系统响应快速且稳定性好。稳态和扰动条件下的测试结果表明张力控制系统控制精度较高且抗干扰能力强。