Mode decomposition methods and their application inground penetrating radar data processing

ZHOU Weifan, ZENG Zhaofa* and LI Jing

1.College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026, China;2.Ministry of Land and Resources Key Laboratory of Applied Geophysics, Changchun 130026, China

Abstract: Ground Penetrating Radar (GPR) method is a widely used method in engineering geophysical exploration at home and abroad. Compared with other geological exploration methods, the GPR method has the advantages of faster detection, higher resolution, convenient operation and relatively low detection cost. With the wide application and continuous development of GPR methods, the processing and interpretation of GPR data is increasingly important. The authors introduce the development process and current situation of the modal decomposition method in processing GPR data, summarize the principles of four modal decomposition methods, and compare their advantages and disadvantages in ground penetrating radar data processing. The results show that when the quality of GPR data is good and the noise is small, Empirical Mode Decomposition (EMD) and Ensemble Empirical Mode Decomposition (EEMD) methods can be used for processing, whereas when the noise interference is large or the underground medium is complex, Complete Ensemble Empirical Mode Decomposition (CEEMD) and Variational Mode Decomposition (VMD) methods can be used for processing. The four modal decomposition methods have their own advantages and disadvantages in GPR data processing. At present, the processing of GPR data by CEEMD and VMD methods is the focus of research and discussion at home and abroad.

Keywords: Ground Penetrating Radar; mode decomposition; IMF; mode-mixing

0 Introduction

The detection method of GPR mainly uses high frequency electromagnetic waves for detection. On the ground, the electromagnetic wave is emitted by the transmitting antenna, and its dominant frequency is several tens of MHz to one thousand MHz. The electromagnetic wave is transmitted to the detection target and received by the receiving antenna to obtain an image of the subsurface target. Ground penetrating radar method is commonly used in engineering geological exploration. During the detection process of ground penetrating radar, the transmitted signal is nonlinear and non-stationary. Moreover, the received signal usually contain a lot of clutter and noise due to a variety of factors, such as the structure of the underground medium, different physical parameters and the system error of the instrument. In order to obtain high quality radar signals, noise and clutter need to be removed. Therefore, it is of great significance to study the signal processing method of ground penetrating radar to get good quality data.

In the traditional Fourier transform, the method of processing the signal is to convert it from time domain to frequency domain, but some minor variations in time domain are unclear. Therefore, Huangetal. (1998) developed EMD method. EMD method is an adaptive signal processing technique for nonlinear and non-stationary signals. This method proposes a new Hilbert-Huang transform based on the Hilbert transform. Compared with the traditional signal analysis method based on Fourier transform, EMD method’s high resolution and adaptability allow the signal to be directly decomposed according to its characteristics. At the same time, after decomposing the signal by EMD method, the purpose of separating the noise and the effective signal can be achieved by selecting different Intrinsic Mode Function (IMF) components, and the noise can be suppressed. However, there are many problems in EMD method, such as lacking of theoretical mathematical models, sensitivity to noise, occurrence of false IMF components, severe mode-mixing effect and so on. Wu and Huang (2009) proposed EEMD method to solve the problems in EMD method. EEMD method is based on EMD method, and the same order of Gaussian white noise is added before EMD method decomposes the signal, and the obtained same-order components are averaged. The purpose of the averaging is to reduce or eliminate the effect of intermittent signals on the overall signal, thereby solving the mode-mixing effect. EEMD method solves some problems of EMD method, but at the same time, new problems have emerged. For example, the newly added Gaussian white noise is not cleaned, the number of IMF components varies from signal to signal, and the original signal cannot be completely reconstructed. Based on the problems of EEMD method, Torresetal. (2011) proposed a new improved algorithm-CEEMD. The CEEMD method also aims at removing clutter and noise. Unlike EMD method, CEEMD method adds Gaussian white noise in each phase of the decomposition process, and finally obtains different IMF components by the uniqueness of the residual. This ensures that CEEMD method can reconstruct the original signal and can reduce the number of calculations and better solving the mode-mixing effect. However, CEEMD method also has some problems, such as the IMF component is not strictly defined by mathematical theory, sensitive to noise, and so on. Dragomiretskiy and Zosso (2014) proposed VMD method. The important thing in VMD method is to solve the problem that there lacks mathematical model and the algorithmic theoretical basis is not strong in EMD, EEMD and CEEMD methods. EMD method is recursive decomposition in the time domain, and VMD method is non-recursive variational mode decomposition in the frequency domain, so its theoretical basis is stronger. VMD method uses iteration to find the optimal solution, and then determines the center frequency and bandwidth of the IMF component. Finally, the separation of the IMF component is completed, and the mode-mixing effect is also greatly solved. VMD method also has some problems, such as poor processing of low-noise background data, no large-scale research applications etc.

After EMD method was proposed, Huangetal. (1998) applied it to the processing of seismic data. Yang (2009) applied EMD method to the data processing of GPR for the first time. The results show that the instantaneous frequency profile obtained by the IMF component decomposed by EMD method is significantly clearer than the original signal profile, and has a higher resolution for the subsurface target. Fengetal. (2012) and Wangetal. (2015) respectively used EMD method to denoise GPR data, which further improved the resolution of data interpretation. Wangetal. (2010) used EEMD method for radar wall penetration experiments, which partly corrected the problem of mode-mixing effect. Xuetal. (2015) used EEMD method in GPR data processing to remove noise. Li (2014) used CEEMD method to process GPR data, further corrected the mode-fixing effect, and improved the interpretation accuracy of GPR data. Chenetal. (2016) added the Hilbert-Huang transform to process GPR data on the basis of CEEMD method, obtained the instantaneous frequency spectrum of Hilbert transform, determined the physical meaning of the instantaneous parameters, and verified that the instantaneous feature profile has higher resolution. Since VMD method was proposed, it has not been widely used in geophysical data processing. Xue (2017) applied it to seismic data processing, which verified that VMD method has better signal decomposition ability and better resolution, and can better determine the position of underground targets. Zhangetal. (2018) used VMD method to process GPR data, which verified the rationality and effectiveness of VMD method in GPR data denoising. Because VMD method is relatively new, it is not used in the field of engineering geophysical yet.

This paper introduces the principles of several modal decomposition methods for processing ground penetrating radar data, explains the advantages and disadvantages of various methods, and then summarizes and analyzes the process history and current situation of modal decomposition at home and abroad and proposes the future trend.

1 Methods

The main role of modal decomposition method in ground penetrating radar data processing is to deal with non-stationary and nonlinear signals. After decomposing to obtain differentIMFcomponents, the effect of suppressing noise on ground penetrating radar data can be achieved by flexibly selecting the IMF component of the effective frequency range.

1.1 EMD

EMD method is to decompose the signal into multiple IMF. Different IMF components contain signals of different frequencies and are then selected and processed.

During the use of EMD method, some conditions must be noted to ensure the normal operation of the method, such as the signal must be a non-monotonic function, setting the characteristic time scale, and when the signal only has an inflection point, it must first be deducted and then integrated. It can be summarized as the following steps:

(1)Initializing, calculating theIMFcomponent.

IMFi=ci(t)

(1)

First find the maximum and minimum in the signal, After interpolation, the upper envelope curvem(t) and the lower envelope curven(t) are defined and averaged.

(2)

Subtracting the mean signal from the original signal.

(3)

(2) Subtractingc1(t) from the original signal, repeat the above process to getIMF2,IMF3and other components, i.e.c2(t),c3(t)…cn(t).

(3) By decomposing multiple times, the original signal can be decomposed into multipleIMFcomponents and a small fraction of acceptable residual component.

(4)

In the processing, it is also necessary to make some provisions on the judgment of theIMFcomponent, including setting the difference between the extreme value point number and the null number as 0 or 1, and the difference of the upper envelope and the lower envelope is 0 and so on.

The mathematical theory of EMD method is relatively simple. Although the signal can be decomposed, the mode-mixing effect is more serious.

1.2 EEMD

EEMD method is a new method based on EMD method. Its basic principle is consistent with EMD method, the only difference is that a fixed ratio and a fixed number of Gaussian white noises are added before EMD method decomposes the signal, taking the original signal and noise as a whole and then decomposing it with EMD method. The significance of adding Gaussian white noise is: Gaussian white noise is uniformly present in the entire space, and the natural frequency of the signal can be added to the uniform Gaussian white noise frequency; the entire process requires multiple random Gaussian white noises to be added multiple times, and they are uncorrelated and have a mean of zero. Therefore, the result of EEMD method can be obtained by taking the mean of all IMF components of EMD method. The mode-mixing effect occurs in EMD method when dealing with intermittent signals or signals with similar frequencies. After adding Gaussian white noise, the extreme points will be redistributed, and the IMF component can be extracted from it, thus solving the mode-mixing effect.

It should be noted that the above process needs to be performed multiple times. That is, adding I times of noise and finally taking the average of the obtained I IMF components, and ensuring that the Gaussian white noise added for I times is different.

(5)

Wheremis the number of noise additions.

EEMD method partially improves the severe mode-mixing effect of EMD method by adding Gaussian white noise, but it cannot reconstruct the original signal perfectly, and some signals have mode-mixing effect.

1.3 CEEMD

CEEMD method is a further improved method based on EMD method and EEMD method. The main difference between CEEMD method and EEMD method is CEEMD method adds different Gaussian white noise multiple times when EMD method generatesIMF1. Averagex(t)+εωi, then getIMF1and generate first order residuals.

(6)

Then continue to decomposer1+εE1[ωi] and produce i-order residuals. When entering the next step to calculate theIMFi+1component, Gaussian white noise is added until the decomposition ends. Moreover, when calculating each order ofIMFcomponents, different Gaussian white noises are added and decomposed multiple times and averaged. Finally, it can be verified that the original signal can be completely reconstructed.

(7)

CEEMD method solves the problem that EEMD method cannot reconstruct the original signal, and it improves a lot on the mode-mixing effect, but its operation time is longer.

1.4 VMD

VMD method is inconsistent with the theoretical basis of the first three methods.VMD method mainly determines theIMFcomponent parameters by determining the optimal solution of the variational model. The definition and meaning of theIMFcomponent is different from the previous methods. In VMD method, theIMFcomponent is an AM-FM signal, i.e.uk(t)=Ak(t)cos(φk(t)). So the most important issue is to solve a equality constraint, that is, how to select multipleIMFcomponents (uk(t)) so that the sum of their bandwidths is the smallest.

(8)

The specific method is as follows:

Introducing the penalty factor and the Lagrangian factor to obtain a Lagrangian expansion expression.

L({uk},{ωk},λ)=

(9)

Converting theIMFcomponent (uk(t)) to the frequency domain.

(10)

Determining the criteria for terminating the iteration.

(11)

The original signal is decomposed into multiple IMF components and residuals.

(12)

VMD method is different from the EMD, EEMD, and CEEMD methods in principle, and solves the problem that the first three methods are not rigorous in mathematical theory, but there is no clear algorithm flow proof when selecting the penalty parameters.

EEMD method and CEEMD method are algorithms for further processing nonlinear and non-stationary signals derived from EMD method, however, the principle of VMD method is different from the other three methods. However, the four modal decomposition methods decompose the GPR signal into multipleIMFcomponents, and then denoise the GPR data and determine the target band signal by flexibly selecting theIMFcomponent.

2 Application

In order to compare the application effects of the four methods, the synthetic benchmark signal and the GPR data are processed by the four methods. Through the different signal data processing results, the advantages and disadvantages of the four methods of EMD,EEMD,CEEMD and VMD in processing GPR data are summarized.

Firstly, EMD method is used to process a radar signal simulated by a sinusoidal signal(Fig.1). The signal consists of 2 Hz, 20 Hz and 100 Hz. It can be seen from the decomposed IMF1-IMF3 that EMD method can effectively separate the signal frequencies.

EMD method is used to process the GPR data of an underground pipeline in the Chaoyang Campus of Jilin University and compare it with the original profile (Figs.2,3)，which proves that EMD method can make the profile more accurate and with higher resolution under certain geological conditions.

The mathematical theory model and algorithm of EMD method are relatively simple, and the corresponding calculation amount is small, which is suitable for processing ground penetrating radar data with uncomplicated underground media. The disadvantages are as follows:

(1) The mode-mixing effect is serious.

(2) When the background noise is obvious, the IMF component of EMD decomposition cannot distinguish the effective information.

(3) Decomposing components with similar frequencies is very difficult.

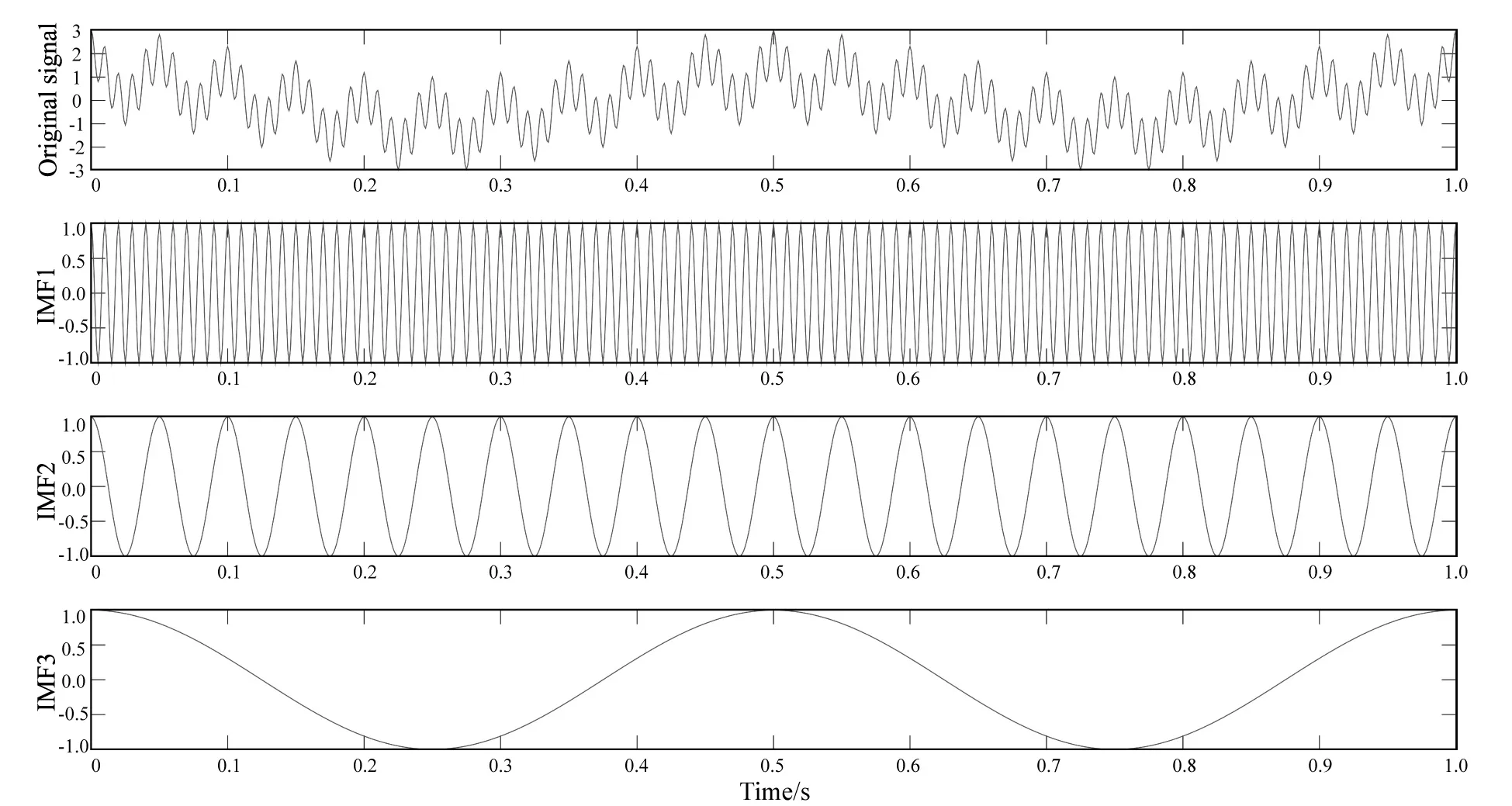
Fig.1 Decomposition of sinusoidal signal with EMD method

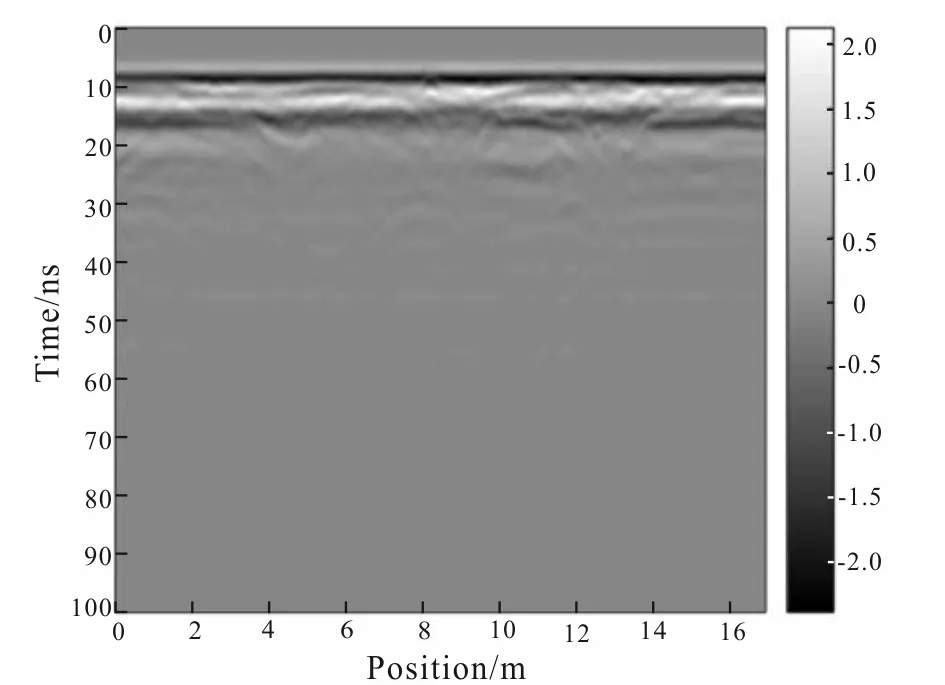
Fig.2 Original section of GPR data

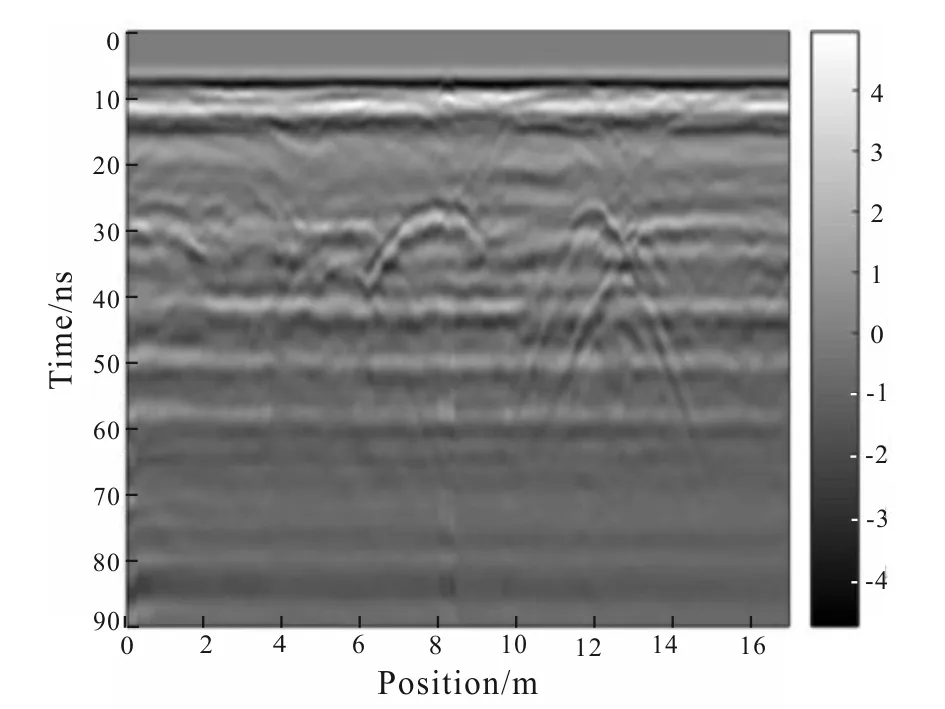
Fig.3 Reconstructed section after EMD method

Subsequently, another complex sinusoidal signal is used to simulate the GPR signal and decompose it with EMD and EEMD methods.

Finally, the results are compared and analyzed (Fig.4a, b). The sinusoidal signal consists of 2 Hz,20 Hz,100 Hz,150 Hz and 200 Hz. It is obvious that the IMF2-IMF6 in EMD method has different degrees of the mode-mixing and the mode-mixing effect is very serious as a whole. EEMD method partially solves the mode-mixing effect of EMD method in this signal.

EEMD method is an improvement based on the principle of EMD method, and solves the mode-mixing effect of EMD method to a certain extent. The accuracy of the analysis of the ground penetrating radar data resolution is increased by adding Gaussian white noise. However, EEMD method also has some short comings, as follows:

(1) The number of times that Gaussian white noise is added cannot be fixed. It should be selected many times as possible, but it requires a lot of calculation. If the ratio is too small, white noise does not work, conversely, if the ratio is too large, white noise covers the active components in the GPR data.

(2) The IMF component cannot reconstruct the original signal, and mode-mixing effect still exists. Meanwhile, it can be seen that CEEMD method completely eliminates the mode-mixing effect and effectively separates the five frequencies in the sinusoidal signal (Fig.4c).

CEEMD method first solves the problem that the signal in EEMD cannot be completely decomposed, and the mode-mixing effect is also greatly improved. For ordinary GPR data, CEEMD method can have better response and interpretation results. However, CEEMD method also has the following problems: ①It takes a lot of computing time; ②the IMF component needs to be manually selected; ③some noise still exists in the IMF component.

The composite signal consists of a 50 Hz sine wave, 0.1-0.2 s, 0.4-0.5 s, 0.7-0.8 s, 0.0-0.5 s cosine wave and Gaussian white noise (Fig.5). EMD, EEMD, CEEMD, and VMD methods are used to decompose and compare the simulated GPR signal with Gaussian white noise as noise (Fig.6). It is verified that when the mode-mixing effect occurs in EMD, EEMD and CEEMD methods, VMD method does not exhibit mode-mixing effect, and has the effect of extracting effective frequency bands.

VMD method differs greatly from the first three methods. In the process of decomposing the IMF component, VMD method solves the problem that the first three methods lack strict mathematical theory. And the denoising effect of VMD is better than the other three methods, which has a better effect of suppressing noise. At the same time, VMD method can more clearly and accurately separate the GPR signal in the frequency domain. However, there are some problems with VMD method, such as: ①The choice of penalty parameters and IMF components is too dependent on experience, and there is no strict calculation process; ②it cannot effectively decompose low frequency noise of GPR data.

(a) EMD decomposition; (b) EEMD decomposition; (c) CEEMD method.Fig.4 Sinusoidal signal decomposition with different methods

Fig.5 Simulated GPR signal and its component signals

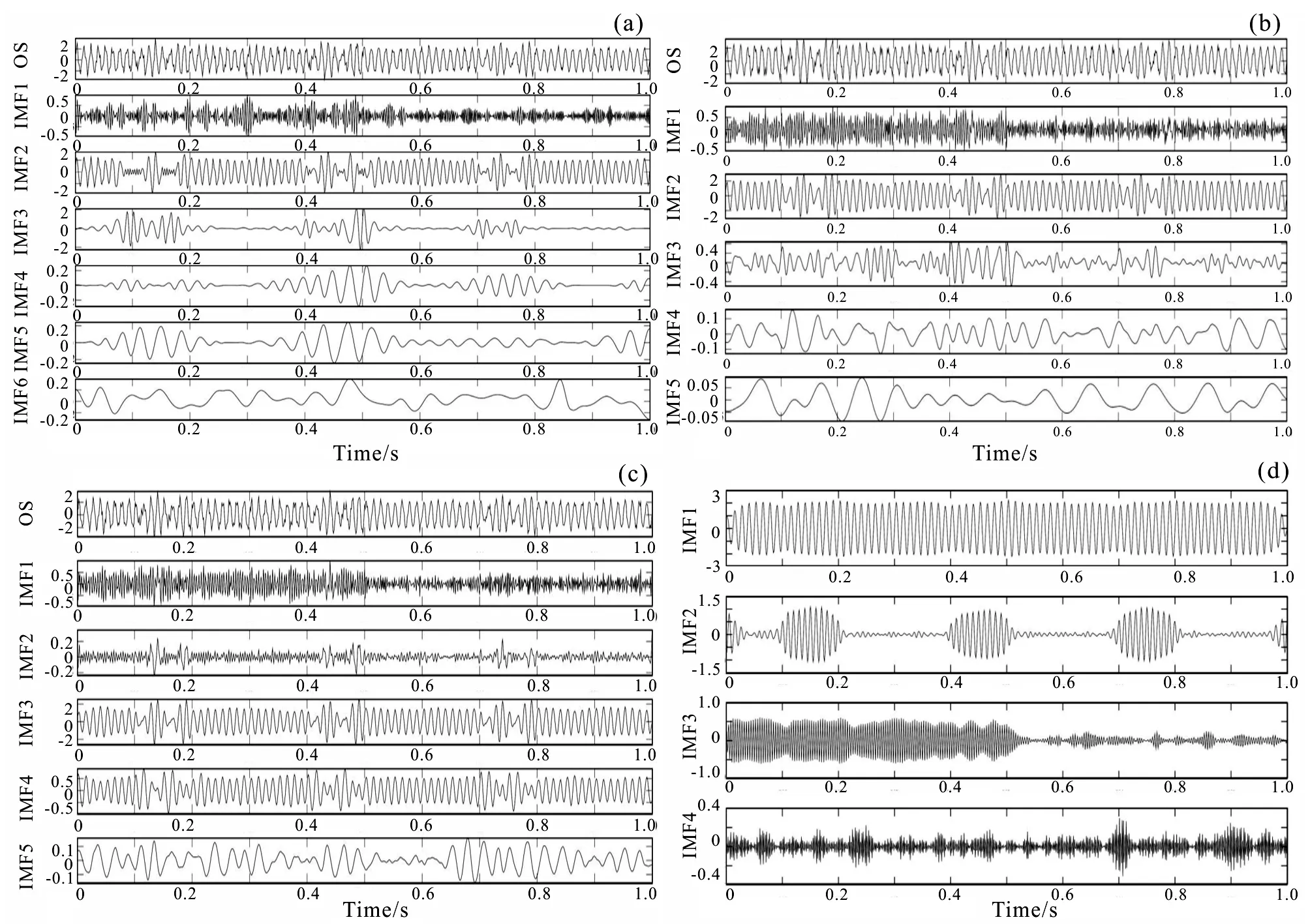
(a)EMD method; (b) EEMD method; (c)CEEMD method; (d) VMD method.Fig.6 IMF components of simulated GPR signals with different methods

3 Conclusions

This paper summarizes the application principles of four modal decomposition methods (EMD, EEMD, CEEMD, VMD) in ground penetrating radar data and summarizes and analyzes their advantages and disadvantages.

(1) Through the comparative analysis of the model, the superiority of the modal decomposition method in dealing with GPR data denoising is verified, which can play the role of signal denoising and determining the target frequency band.

(2) Through the processing and analysis of the simulated GPR signal, it is verified that EMD and EEMD methods are suitable for GPR data processing with simple terrain, uniform underground media around the target, and low interference noise, because EMD method is simple and have a short running time. However, in processing GPR data of complex geological structure, the mode-mixing effect is too serious.

(3) By comparing the simulated GPR signal, it is verified that the CEEMD method has a good suppression of the mode-mixing effect. For most GPR data, the effective frequency separation of the signal can be performed by decomposing the IMF component. However, in the specific calculation process, it takes long time, and it needs to perform multiple measurements in the calculation time and the denoising result in order to continuously obtain better denoising effect. Moreover, for complex terrain or data with strong noise, it is still difficult to remove noise in the IMF component decomposed by CEEMD method.

(4) By simulating the GPR signal and comparing the processing results of the four modal decomposition methods, the validity and correctness of VMD method for GPR data processing denoising are verified. VMD method has a strict proof process in mathematical theory. However, since this a relatively new method, there is no large-scale application in GPR data processing and research yet, and the method itself needs to manually select the IMF component, so it is necessary to continue with in depth study.

(5) Comparing the advantages and disadvantages of the four modal decomposition methods in GPR data processing results, it is speculated that CEEMD and VMD methods are the future research focuses and hotspots.