Slope reliability analysis based onMonte Carlo simulation and sparse grid method

WU Guoxue, PENG Yijin, LIU Xuesong, HU Tao and WU Hao*

1．College of Earth Sciences, Jilin University, Changchun 130026, China;2．School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China

Abstract: In order to solve the problem of the reliability of slope engineering due to complex uncertainties, the Monte Carlo simulation method is adopted. Based on the characteristics of sparse grid, an interpolation algorithm, which can be applied to high dimensional problems, is introduced. A surrogate model of high dimensional implicit function is established, which makes Monte Carlo method more adaptable. Finally, a reliability analysis method is proposed to evaluate the reliability of the slope engineering, and is applied in the Sau Mau Ping slope project in Hong Kong. The reliability analysis method has great theoretical and practical significance for engineering quality evaluation and natural disaster assessment.

Keywords: slope reliability analysis; high-dimension; sparse grid; Monte Carlo simulation

0 Introduction

Slope is usually formed naturally or by construction process. The instability of natural slope can cause landslides, debris flow and other disasters, while the instability of artificial slope will lead to collapse or poor quality construction project. Therefore, the reliability analysis of slope stability is of great importance to engineering quality evaluation and natural disaster prevention. There are many traditional slope reliability analysis methods such as limit equilibrium method, limit state method, numerical analysis method etc. However, these deterministic methods do not take into account the uncertainties of a series of basic design parameters of slope engineering, and the results of the analysis cannot accurately reflect the stability of the actual slope. In recent years, the randomness of the slope system have been fully realized, and reliability analysis method is introduced by researchers as an effective scheme to evaluate the safety of the slope system, such as Monte Carlo simulation (MCS) (Sekhavatian & Choobbasti1, 2018), first order reliability method (FORM) (Vanem, 2018), response surface method (RSM) (Yangetal., 2014). Because of the high complexity of engineering problems, only a complex high-dimensional reliability analysis model can be established in most instances. Among the existing reliability analysis methods, FORM is of high efficiency, but the accuracy of dealing with complex high-dimensional model is too low because its established model is too ideal. MCS is easy to operate, but it often requires a lot of sampling in order to obtain stable results, especially for those slopes with small failure probability, the efficiency is very low, which is not practical.

With the development of numerical discrete technology, researchers have proposed a sparse grid sample space (Gerstner & Griebel, 1998), which is more advantageous than the full grid sample space. In sparse grid sampling, the number of sampling points is greatly reduced in the meantime of ensuring the accuracy of sampling. When the dimension of sample space is increased, the number of sample points does not increase geometrically with the dimension, thus the computational efficiency is improved. Based on this, the authors study the sparse grid and the reliability analysis method based on the approximate model, and combine the sparse grid method and the approximate simulation method to maintain the high precision and solve the curse of dimension (Barthelmannetal., 2000) problems encountered in high dimensional reliability analysis, so that the computational cost is no longer dependent on the dimension index. The Monte Carlo simulation method based on sparse grid method is developed to improve the efficiency and precision, and it is more suitable for slope reliability analysis.

1 Reliability analysis and sparse grid method

1.1 Reliability overview

1.1.1 Engineering system limit state

When the whole or part of the engineering system exceeds a certain state, which cannot meet one of the designed functional requirements, the specific state of the engineering system is to become the limit state (Zhang, 2009). The limit state is the critical state between reliable and unreliable states of the engineering system. So, a performance function of structure can be set up according to the functional requirements and the limit state of the engineering system.

Z=g(X)=g(x1,x2,x3,…,xn)

(1)

whereX=(x1,x2,…,x3) indicates random variable,xi(i=1,2,…,n) indicates parameter that determines the design performance of the engineering system,Z>0 indicates that the engineering system is in a reliable state,Z<0 indicates that the engineering system is in an unreliable (failure) state, andZ=0 indicates that the engineering system is in the limit state. Correspondingly, the limit state function of engineering system is expressed as

Z=g(X)=g(x1,x2,…,xn)=0

(2)

It is also called limit state face. Apparently, the limit state face divides the definition domain into two regions: reliable domainΩsand failure domainΩf. In reliable domain,Z=g(X)>0,∀X∈Ωs, on the contrary, in failure domain,Z=g(X)≤0,∀X∈Ωf.

1.1.2 Engineering system failure probability

The ability of the engineering system to perform a predetermined function within a specified time and under defined conditions is called engineering system reliability. Safe probabilitypsis used to indicate the probability that the structure can complete an intended function, while failure probabilitypfis used to indicate the probability that the structure cannot complete the intended function。

Considering the functionZof engineering system is a continuous random variable, the probability density function ofZisfZ(z), we can see from the knowledge of probability theory that

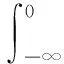
(3)

The joint probability density function of random variablesX=(x1,x2, …,xn) isfx(x), so the failure probability of the engineering system is expressed as

(4)

1.2 Monte Carlo simulation

One of the main tasks of Monte Carlo simulation is to generate the corresponding random number from a given probability distribution (Dubourgetal., 2011). Given a set of generated random numbers, the simulation process is deterministic. The reliability analysis based on Monte Carlo simulation is to simulate the reliability directly by random sampling.

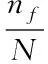
(5)

According to formula (4), the failure probability can be expressed as

(6)

In the above formula,I(Z) is the indicator function of Z. WhenZ≤0,I(Z)=1, whenZ>0,I(Z)=0. So the integral region extends from the non-regular failure domain A to the infinite rule domain, and the integrand is zero in the entireZ>0 region.

According to formula (6), if the joint probability density function of function and random variableare known, we can sample using Monte Carlo simulation directly. According to formula (5), the estimation of failure probability can be obtained.

Although the Monte Carlo simulation is simple in principle, and is widely used, easy to calculate and stable, it still involves large calculation, especially when focusing on the small failure probability problem in practical engineering. If we want to obtain accurate convergence result, it is always not efficient because of the function computational complexity.

1.3 Sparse grid theory

Smolyak theory is the improvement of the direct tensor product method, and it puts forward some constraints on the sample points generated by the direct tensor product method and removes some unnecessary grid points to reduce the computational complexity. This theory approximates the complex model as a set of linear combinations of hierarchical functions based on simultaneous technology. The following is a numerical integration as an example to illustrate its construction process.

First, we consider quadrature formula of one - dimensional functionf(x) of weightedρ(x) when x∈[-1,1]

(7)

l(l∈N) represents the “level” of the polynomial.mlis the total number of integral points of a single variable formula at levell. The coefficientwkis equal to the weight of pointxkat all points. The weight is related to the integral interval, the weight function and the integration point, but it does not depend onf(x).

As for d dimensional problem, the direct tensor product method directly uses the tensor product of the fundamental function of each dimension, and will make the final solution approximately as a linear combination of a set of univariate basis functions (Zabaras & Klimke, 2007; Wohlmuth, 2005).

(8)

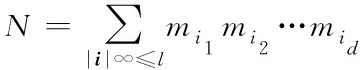
(9)

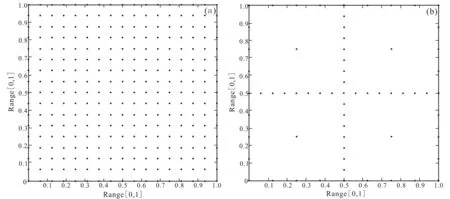
(a) N=17×17=289; (b) N=65.Fig.1 Sample sets of direct tensor method and sparse grid method for two-dimensional problem

Smolyak quadrature formula is

(10)

And the tensor product is defined as

wi1k1wi2k2,…,widkd

(11)

It is worth noting that the multidimensional polynomial leveliand inequalityl≤|i|1≤l+d-1 determine the number of sampling points on each dimension. This inequality about leveliensured that if leveli(n1,n2,…,nN) is a valid indicator, then leveli(n2,n1,…,nN) must also be a valid indicator, which means,i1=n1,n2,i2=n1,n2, and so on. This shows that the sparse grid method evenly treats each dimension, and the levelijobtained on a dimension can be obtained in another dimension, so the sampling points of the sparse grid method are the same in every dimension.

2 Reliability analysis based on Monte Carlo simulation and sparse grid method

2.1 Sparse grid based surrogate model construction

Firstly, the sparse grid method can be used to construct the interpolation approximation model of one - dimensional problem,

(12)

(13)

Among them |i|1=i1+…+id. It can be found that the new interpolation approximation model introduces a limit on the levelij,j=1, …,dof each dimension, limiting the number of sampling pointsmijon each dimension. The Clenshaw-curtis isometric node type is selected for sample points, where the corresponding piecewise linear basis function is

(14)

This is the general sparse grid interpolation method of the construction process (Ma & Zabaras, 2009; Xiongetal., 2010) and does not reflect the choice of nested nature of the role of the set of sample points. But the hierarchical sparse grid interpolation method based on piecewise linear basis function makes good use of this property (Klimke & Wohlmuth, 2005; Ma & Zabaras, 2009). First, we can express the Smolyak formula as (q=l+d-1,q≥d)

(15)

(16)

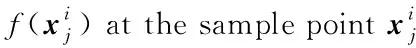
(17)

(18)

Because of the existence of hierarchical surpluses, the hierarchical sparse grid interpolation method of piecewise linear basis function shows the priori precision of the fitting. After the interpolation of each layer is finished, through the hierarchical approximation model, the current fit accuracy can be obtained. When the precision meets the requirements, the refinement of the sample space and the construction of the surrogate model are automatically stopped.

2.2 Reliability analysis method based on surrogate model

This paper presents a reliability analysis method based on high efficiency dimension reduction, by using Monte Carlo Simulation, and constructing surrogate model of performance function via sparse grid method (generalized sparse grid method), so as to use an explicit simple surrogate model to replace the complex, implicit function, and to improve the efficiency (Xiongetal., 2010; Hu & Youn, 2011).

Fig.2 uses the direct Monte Carlo simulation as an example to compare the differences between the two algorithms. Although both methods use the original function, as for the reliability analysis method based on the direct Monte Carlo simulation, all the sampling results have called a function. In practical application, the number of random variables obtained by Monte Carlo random sampling is often greater than or equal to 105, which is huge. And the reliability analysis method based on the efficient dimensionality reduction only calls the function when constructing the surrogate model. Generalized sparse grid method is an efficient numerical discrete technology, and the number of sample points needed is much smaller than the former. The result of random sampling only calls the surrogate model of the original function, which is simple and easy to calculate, so the number of calls to the original function of the whole algorithm will be greatly reduced. Therefore, when the function is quite complex, even implicit, the reliability analysis method based on high efficiency dimension reduction will be very substantial for the improvement of computational efficiency.

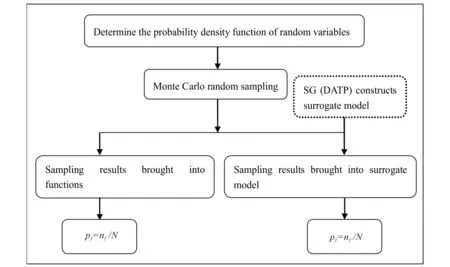
Fig.2 Reliability analysis of direct Monte Carlo simulation and reliability analysis based on surrogate model

3 Reliability Analysis of Sau Mau Ping slope

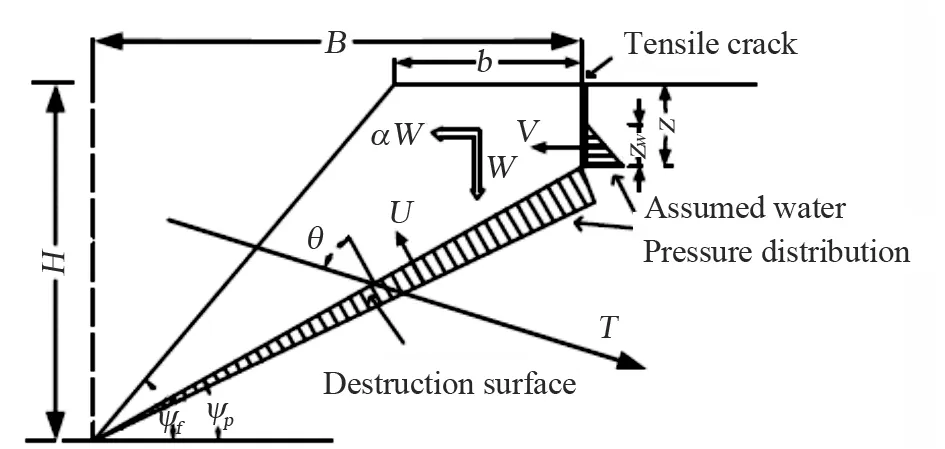
Fig.3 Sau Mau Ping slope diagram

Many scholars at home and abroad have studied Hong Kong Sau Mau Ping slope (Low, 2007, 2012; Lietal., 2011). The rock slope has a plane slip failure mode, as shown in Fig.3. In this paper, we use Monte Carlo simulation based on high efficiency dimension reduction to calculate its reliability. The safety factor (Low, 2012) can be expressed as:

(19)

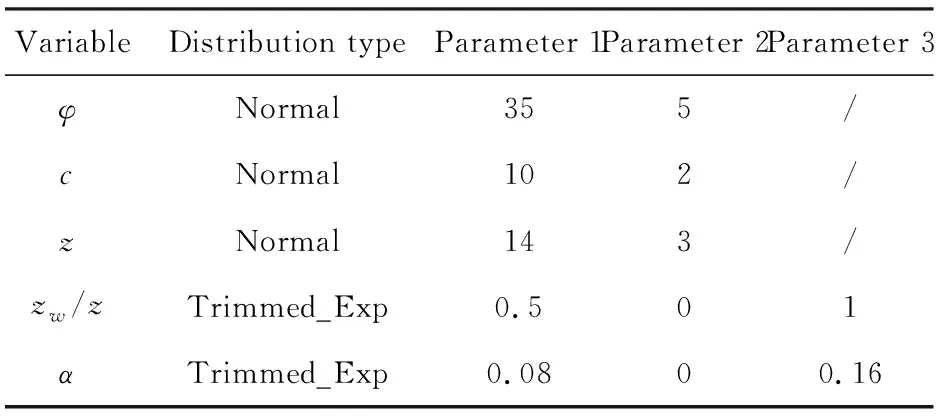
Table 1 Distribution parameters of random variables

In reliability analysis, the DTAP algorithm is used to construct the surrogate model of the performance function. In this paper, a total of 186 sample points are used to build the surrogate model. The Monte Carlo simulation method calls the surrogate model to calculate 1 million times to obtain the failure probability of 2.27%. The failure probability is basically the same as the result of the original function calling 1 million times. When the original function is implicit function which is difficult to calculate, this kind of surrogate model based on efficient sparse grid methods becomes very important. As for the calculation cost of surrogate model, which is constructed by certain high confidence sample points, is very low. The Monte Carlo simulation method based on this surrogate model can not only guarantee the accuracy of calculation, but also ensure the efficiency of calculation.

4 Conclusion

This paper is devoted to the study of the reliability analysis method for high dimension problem, and solves the problem of low efficiency of general method. The contents of this paper are mainly divided into numerical discrete techniques represented by sparse grid and reliability analysis method based on Monte Carlo simulation. First, a numerical discrete technique-sparse grid is studied, and then an interpolation method which can adapt to the high dimension problem is proposed. Subsequently we introduce the method into the reliability analysis based on Monte Carlo simulation to replace the original function with a surrogate model, to make the new reliability analysis method more efficient. The method proposed in this paper is applied to the reliability analysis of the Sau Mau Ping slope in Hong Kong. While ensuring the accuracy of Monte Carlo simulation, the method greatly improves the efficiency of the method, which makes the Monte Carlo simulation method applicable to the reliability analysis of slope engineering. In summary, it effectively improves the calculation efficiency of the slope reliability analysis process.