Regularized focusing inversion for large-scalegravity data based on GPU parallel computing

WANG Haoran, DING Yidan, LI Feida and LI Jing

1.College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026, China;2.Jilin Geophysics Prospecting Institude, Changchun 130062, China

Abstract: Processing large-scale 3-D gravity data is an important topic in geophysics field. Many existing inversion methods lack the competence of processing massive data and practical application capacity. This study proposes the application of GPU parallel processing technology to the focusing inversion method, aiming at improving the inversion accuracy while speeding up calculation and reducing the memory consumption, thus obtaining the fast and reliable inversion results for large complex model. In this paper, equivalent storage of geometric trellis is used to calculate the sensitivity matrix, and the inversion is based on GPU parallel computing technology. The parallel computing program that is optimized by reducing data transfer, access restrictions and instruction restrictions as well as latency hiding greatly reduces the memory usage, speeds up the calculation, and makes the fast inversion of large models possible. By comparing and analyzing the computing speed of traditional single thread CPU method and CUDA-based GPU parallel technology, the excellent acceleration performance of GPU parallel computing is verified, which provides ideas for practical application of some theoretical inversion methods restricted by computing speed and computer memory. The model test verifies that the focusing inversion method can overcome the problem of severe skin effect and ambiguity of geological body boundary. Moreover, the increase of the model cells and inversion data can more clearly depict the boundary position of the abnormal body and delineate its specific shape.

Keywords: large-scale gravity data; GPU parallel computing; CUDA; equivalent geometric trellis; focusing inversion

0 Introduction

With the continuous development of geophysical exploration equipment and technology, the need to process large volume geophysical data quickly and accurately has also increased, and a lot of researches have been done on how to improve the accuracy and speed of inversion. However, most methods to improve the accuracy of inversion cannot handle the whole 3D inversion of large area in actual data processing, due to the limitation of computer memory and CPU computing efficiency. Therefore, reducing memory usage and improving computing efficiency have become urgent issues to be solved.

A current procedure in 3D inversion is dividing the underground source region into a set of regular juxtaposed cuboids. For the calculation of sensitivity matrix, the memory required to store and computation time will increase with the number of juxtaposed cuboids. Li & Oldenburg (2003) performed wavelet transform on the sensitivity matrix and reset threshold and assign those below threshold as 0 to form a sparse matrix. The sensitivity matrix still needs to be calculated and there exists a certain loss of information, although this method reduces computation and memory footprint to some extent. Yaoetal. (2003) proposed an equivalent geometric trellis concept based on the equivalence of shift and the symmetry reciprocation, and thus the huge storage needed for large models is reduced tremendously.

Compared with CPU computing technology, GPU has obvious advantages in processing capacity and memory bandwidth. With the characteristics of low cost, high performance and fast speed, GPU has certain applications in large-scale potential field inversion where the modeling domain is discretized into billions of cells. Moorkampetal. (2010) used GPU parallel technology to implement gravity and gravity gradient forward modelling. Chenetal. (2012) proposed the optimized parallel reduction strategy for forward calculation based on CUDA, meanwhile, the strategy of GPU parallel computing in two inversion methods is also discussed. Cuma & Zhdanov (2014) utilized combined MPI and OpenMP coding and a mixed single-double precision approach to realize magnetic data inversion. Lietal. (2016) introduced multiple thread invocations and sensitivity range searches to improve the GPU parallel programming. Zeng (2016) used the separate framework technology to further optimize the GPU forward calculation; Hou (2016) used OpenMP-CUDA hybrid programming to implement the correlation imaging algorithm. Yuetal. (2017) applied GPU parallel processing to 3-D genetic gravity inversion in Xisha Basin.

To improve the accuracy and efficiency of inversion, this paper proposed a regularized focusing inversion method utilizing GPU parallel architecture on the basis of previous researches, which overcomes the huge memory footprint, low efficiency and time consuming issues in the inversion for massive data, and lays the foundation to invert regional to continental size data with up to billion cells for interpretation of large airborne gradiometry surveys. The equivalent geometric trellis is adopted to compute the sensitivity matrix, and the parallel forward modeling and inversion are on multi-GPU control with Openmpi.

The paper briefly describes the theory behind the 3-D potential field inversion, and present our approaches in forward modeling and inversion in details and show the performance of our method through several scenarios. The acceleration effect and inversion results are then analyzed and discussed.

1 Theory

1.1 Forward modeling and equivalent geometric trellis

The purpose of gravity forward modeling is to calculate the effect of subsurface density distribution on the observation surface. Firstly, the modeling domain is discretized into several cells of constant density (Fig.1).

The discrete forward modeling can be expressed in general matrix notations as:

d=Am

(1)

wheredis a vector of the observed data of the ordern,mis a vector of the model parameters of the orderm, andAis called the sensitivity matrix that is a matrix of a sizen×m, formed by the corresponding gravity field kernels. If the subsurface modeling region is divided intonx×ny×nzgeometric cuboids, thenn=nx×ny，m=nx×ny×nz.

The gravity anomaly generated by any geometric cuboidMat the observation pointDcan be expressed as:

ΔgDM=ρMSDM

(2)

where

(3)

whereGis the gravitational constant and is the density of the geometric cuboid,

SDMis called geometric trellis and it is the element that makes up the sensitivity matrixA. It can be seen that it has nothing to do with the density of each geometric cuboid of the model, but only with the position of the observation point relative to the geometric cuboid.

(a) A layer of rectilinear cuboids; (b) a single cuboid. Position of the observation is described by the coordinate triple (x,y,z). Coordinates of corners of the cuboid can be completely described by two triples (x1,y1,z1) and (x2,y2,z2).Fig.1 Interpretation models

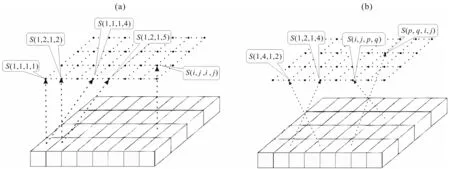
(a) The equivalence of shift; (b) the symmetry reciprocation.Fig.2 Properties of geometric trellis

For the sensitivity matrix, the memory required to store and the time to calculate will increase with the growing of the scale of juxtaposed cuboids. In this paper, the sensitivity matrix is calculated by a very skill of equivalent storing proposed by Yao (2003). To make it easy to explain, we introduce the concept of geometric position. For the geometric cuboid located in therth along theXaxis, thesth along theYaxis and thetth along theZaxis, its geometric position is defined as (r,s,t), wherer=1，2，…；s=1，2，…；t=1，2，…，nz. According to this definition, the geometric position of any observation point can be given as:

(4)

And the geometric position of any geometric cuboid can be given as:

(5)

Where [...] means integral function. According to equations (4) and (5), the elements of the sensitivity matrix can be converted into the expressions of the geometric trellis.

Take a layer of juxtaposed cuboids according to the equivalence of shift and the symmetry reciprocation(Fig.2), a geometric cuboidMjof this layer relative to the observation pointDican be written as:

(6)

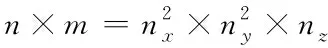
Table 1 shows the memory footprint with different model scales for the traditional method and the equivalent storage of geometric trellis method (both use double precision storage). It shows that the equivalent storage method occupies significantly less memory than the traditional method. When the model cells are too large, the traditional method cannot perform the actual operation because of the limitation of the computer memory. Therefore, the equivalent storage of geometric trellis method provides a possibility for the inversion of large model bodies in aspect of memory.

Table 1 Comparison of memory for sensitivity matrix storage in different methods

1.2 Regularized focusing inversion

The solution of the linear inverse problem is substituted by the minimization of the Tikhonov parametric functional (Tikhonov & Arsenin, 1977):

Pα(m,d)=φ(m)+αS(m)

(7)

Where the misfit functionalφ(m) is specified as:

φ(m)=‖Am-d‖

(8)

And the stabilizerS(m) that can make the inversion result contain a priori information of the model parameters is selected as minimum support functional (Portniaguine & Zhdanov, 2012). Then the corresponding parametric functional can be expressed as:

Pα(m,d)=‖WdAm-Wdd‖-α‖WeWmm-WeWmmapr‖2

(9)

Wheremapris a prior model,Wd,Wm,Weare weighting matrix of data, model parameters and focusing respectively.

The equation (9) is minimized based on the reweighted conjugate gradient method. The reweighted parametric functional can be rewritten as:

(10)

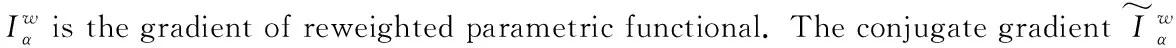
For the first iteration the conjugate gradient direction is defined as the gradient direction:

(11)

For thenth iteration (n=1,2,3...), the conjugate gradient direction is defined as the linear combination of the gradient on this step and the conjugate gradient direction on the previous step:

(12)

The successive line search in the conjugate gradient direction can be written as:

(13)

The actual model parameters can be converted as:

(14)

After reweightingmn+1, the stabilizer is updated as:

(15)

To ensure that the misfit functional is focused to the smallest, the following procedures are adopted to reduce the regularization factor. First let

(16)

and then update the regularization factor as follows:

(17)

If the misfit functional is not shrinking fast enough:

(18)

Then, the value ofαn+1calculated by the equation (17) should be reduced toqtimes of the original value and we selectedq=0.6 according to experience.

When the misfit reaches a given range:

Iteration process terminates and outputmN.

1.3 GPU parallel computing technology

GPU has a highly parallel architecture and powerful computing ability. After several years of development, GPU parallel technology is widely used in scientific computing in various fields. Hardware companies have introduced the GPGPU (General Purpose Computing on GPU) specifically for computation. This paper uses NVidia-CUDA to program and Openmpi for multi-GPUs control. By this means, we have achieved parallel gravity forward modelling and inversion of massive data.

The time-consuming calculation of each part of the gravity inversion on the single-core CPU is first analyzed, and the time-consuming hotspot of the program is found. For models with a scale of 30×30×20 cells, the time consumption of each part is shown in Table 2.

GPU parallel computing technology is used for the relatively time-consuming parts of the program, and the parallel computing program is optimized as follows: reducing data transfer, reducing access restrictions, hiding latency, and reducing restrictions.

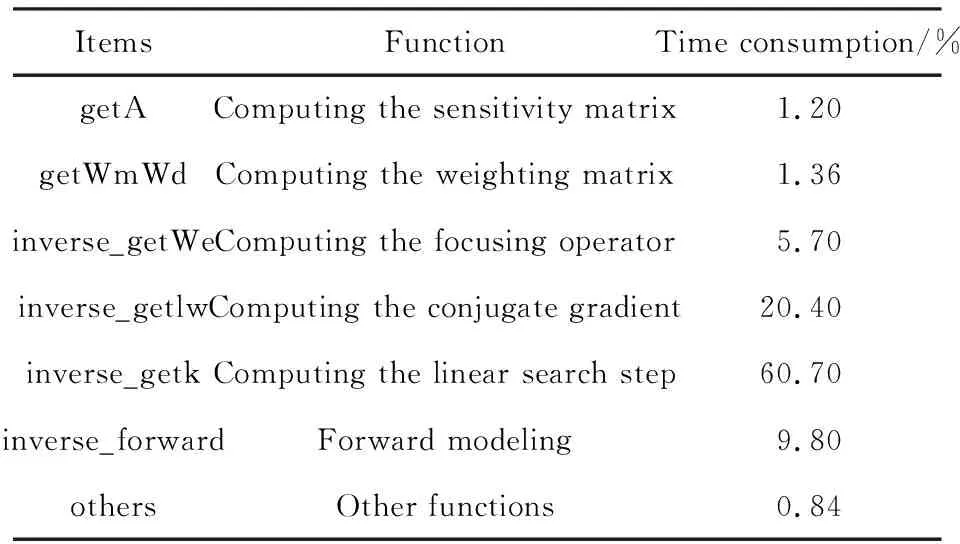
Table 2 Running time of each part of program

1.3.1 Reducing data transfer

GPU has a powerful computing capability. Taking the TESLA P100 as an example, it has 3584 CUDA cores with a counting performance of 4.7 TFLOPS for double-precision and 9.3 TFLOPS for single-precision. However, the communication bandwidth between CPU and GPU is only 32 GB/s, making large-scale data transfer between CPU and GPU time-consuming. It is a waste of immense computing power for the GPU. Table 3 shows the time it takes to transfer data from CPU memory to GPU memory for models of different scales.

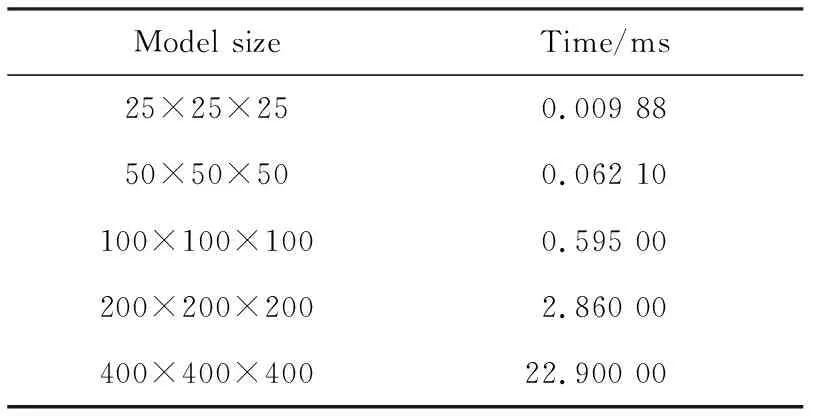
Table 3 Transfer time for different scale models

Table 3 shows that the data transfer time is proportional to the amount of data. So when designing GPU parallel program, we should try to keep the data in GPU to reduce the large-scale data communication between GPU and CPU. CPU is used as the host that is responsible for logical judgment and serial computing while GPU acts as a device for performing highly parallel threading tasks.

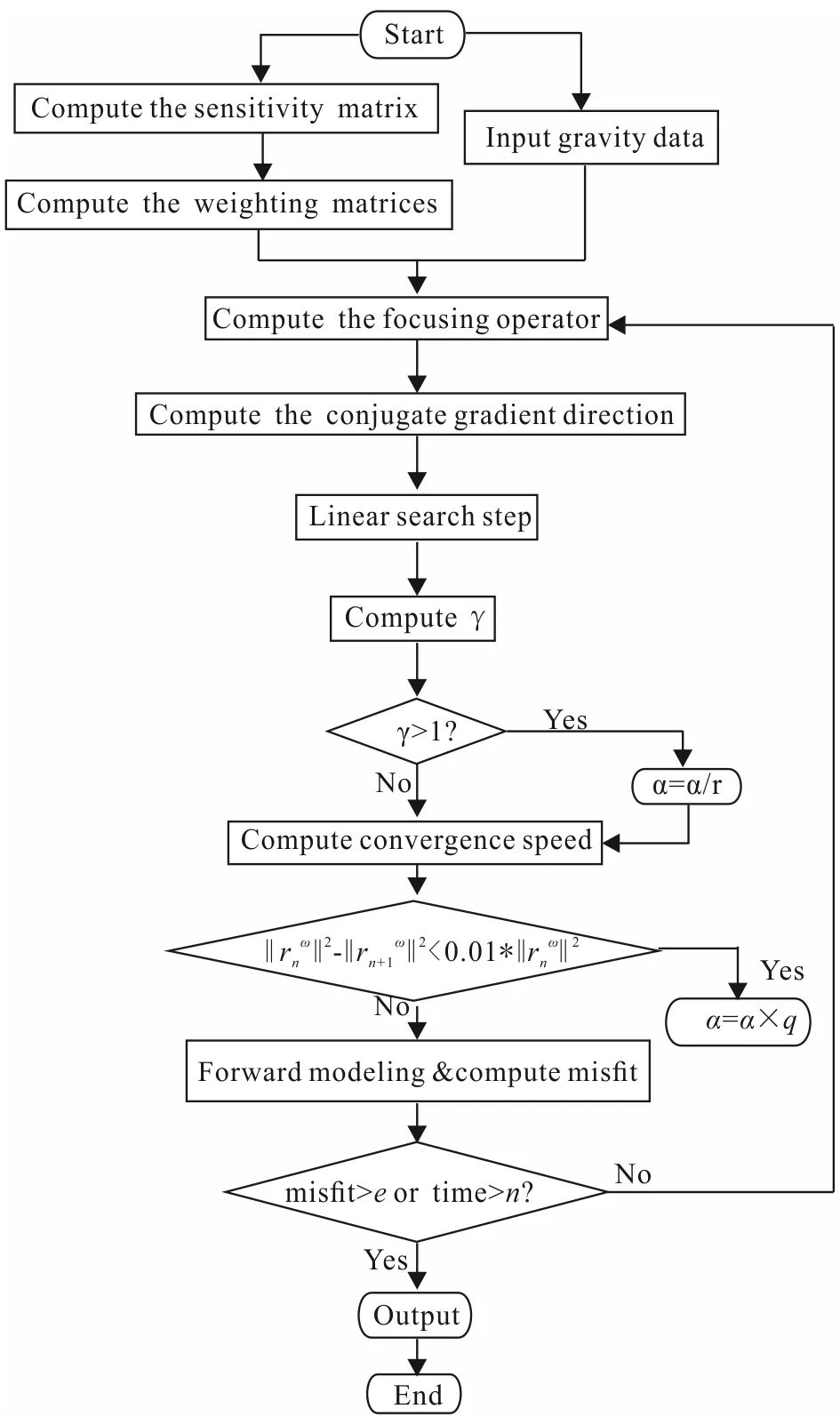
Fig.3 Parallel inversion flowchart

1.3.2 Reducing access restrictions

Again, taking TESLA P100 as an example, its memory bandwidth is 720GB/s but its counting performance is of TFPLOS level. GPU memory access speed is too slow compared to its high-performance computing capacity, which greatly affects the computation efficiency of GPU. For this case of access restrictions, GPU's shared memory, read-only cache and constant cache are used which can greatly improve the efficiency of the program.

1.3.3 Latency hiding

Compared to CPU, most of the chip area in GPU is occupied by the SM computation units. The latency of the computing unit is approximately 20 clock cycles while the latency of accessing GPU memory is 400 to 800 clock cycles. GPU needs to switch between a large number of active threads to hide the latency of computation and memory access. There are three main causes of limiting the hidden delay: ①The active threads are insufficient, so the GPU computing cores cannot be fully utilized. ②The registers are insufficient to start more threads at the same time. ③The amount of shared memory is not enough to call more computing units.

Aiming at above problems, relevant approaches are adopted respectively. We use reasonable blockdim and griddim to increase the number of active threads, expand the complex calculation process into several simple steps to reduce the use of registers and use shared memory reasonably to avoid excessive use affecting the latency hiding which means finding an optimal balance between reducing access restrictions and increasing latency hiding.

1.3.4 Reducing instruction restrictions

Instruction restrictions means that GPU instruction units are dispatched too frequently and GPU seems to be busy but actually inefficient. Therefore, high-throughput instructions, instead of low-throughput ones, should be used. This paper replaces double precision (double) with single precision (float) and use the built-in mathematical functions provided by CUDA to replace traditional ones (such as_sinf instead of sin), at the same time reducing the if-else branch.

2 Model study

In this section the acceleration performance of our parallel programming is tested first. Fig.4a shows the computation time of forward modeling for varying model scales between 1×1×1 cells and 512×512×512 cells on the CPU and GPUs. It is indicated that the CPU-based computation time increases at a near-linear trend with model scale. For the GPU-based computations, the consuming time is higher than that of the CPU with models under 32×32×32 cells, resulted from the initialization work on the GPU and extra cost of data transfer between the CPU and the GPU. For models less than 8×8×8 cells, the GPU-based computation time almost keeps the same because the model is relatively small that does not utilize much parallelism of the GPU as finer model discretization does. For models exceeding 64×64×64 cells there is a linear dependency of computation time on the model scale. Within the linear domain, 40×speedup for the GTX 1060 and 70× speedup for the Tesla P100 are achieved respectively compared to a single thread CPU.

Fig.4b shows the inversion computation time for varying model scales between 1×1×1 cells and 256×256×256 cells on the CPU and GPUs. We ran 50 inversion iterations. It can be seen that the curves in Fig.4b have basically the same shape as those in Fig.4a but a little different. For models less than 4×4×4 cells, the GPU-based computation is more time-consuming due to the domination by initialization work and memory transfers. For small-scale models the GPU-based computation time is constant due to the calculation amount is relatively small and as such does not utilize all available computing units on the GPU. The transition from constant computation time to linear increase for the GPUs again occurs at a model scale of 16×16×16 cells，after which the computing performance has reached a plateau. The 50 inversion iterations for a model with 100×100×100 cells using 4 Tesla P100 takes only 2 350 s which reduces the runtime by a further 97% compared to the CPU.

We design an inversion region which is 10×10 km in theXandYdirections and 2.4 km inZdirection, with a Y-shaped body with residual density of 1 g/cm3, buried in depths ranging from 750 to 1 200 m. Fig.5 shows the 3D model and the synthetic observed gravity anomaly on the ground.

To demonstrate the effectiveness of inversion with the large-scale model, three different model scales of 100×100×80 cells, 50×50×40 cells and 25×25×20 cells are implemented respectively. The misfit reached a 3% data error level.

As indicated from Fig.6, the inversion results of the model scale with 25×25×20 cells show poor recovery of the original model while for the model scale with 100×100×80 cells, the horizontal position and the depth are the closest to the actual geological body. As the model is scaled up finer, the spatial resolution is improved significantly, and the inversion results are close to the real model in the aspect of the shape and peak of the abnormal body.

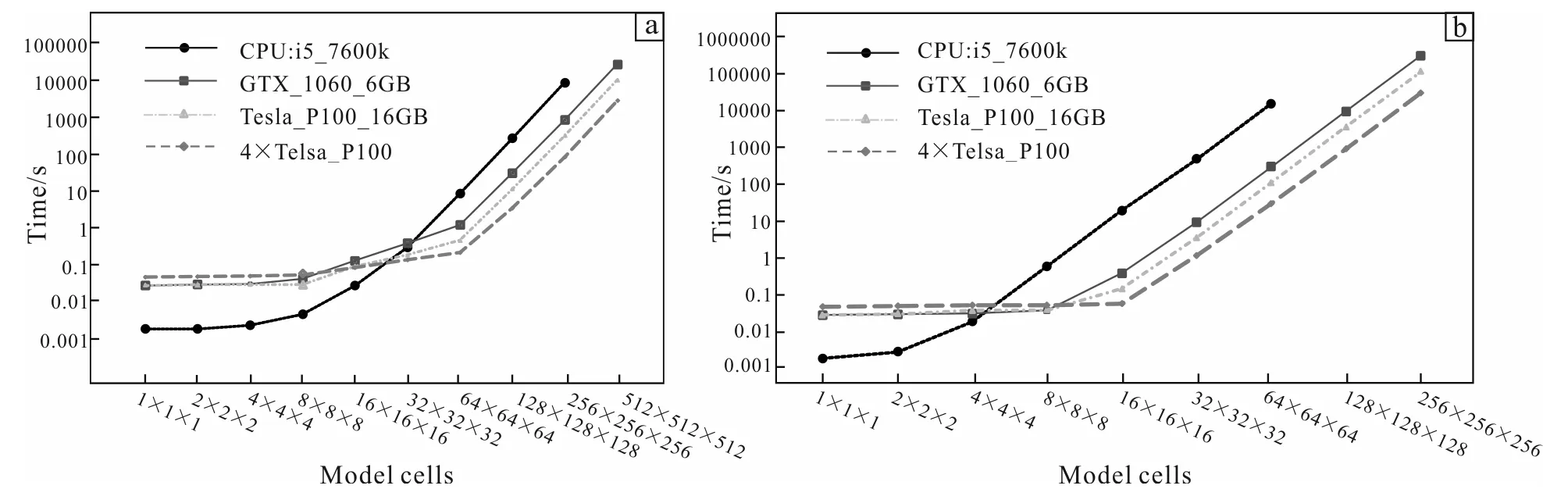
Fig.4 Computation time of forward modeling (a) and inversion (b) for models with different cells

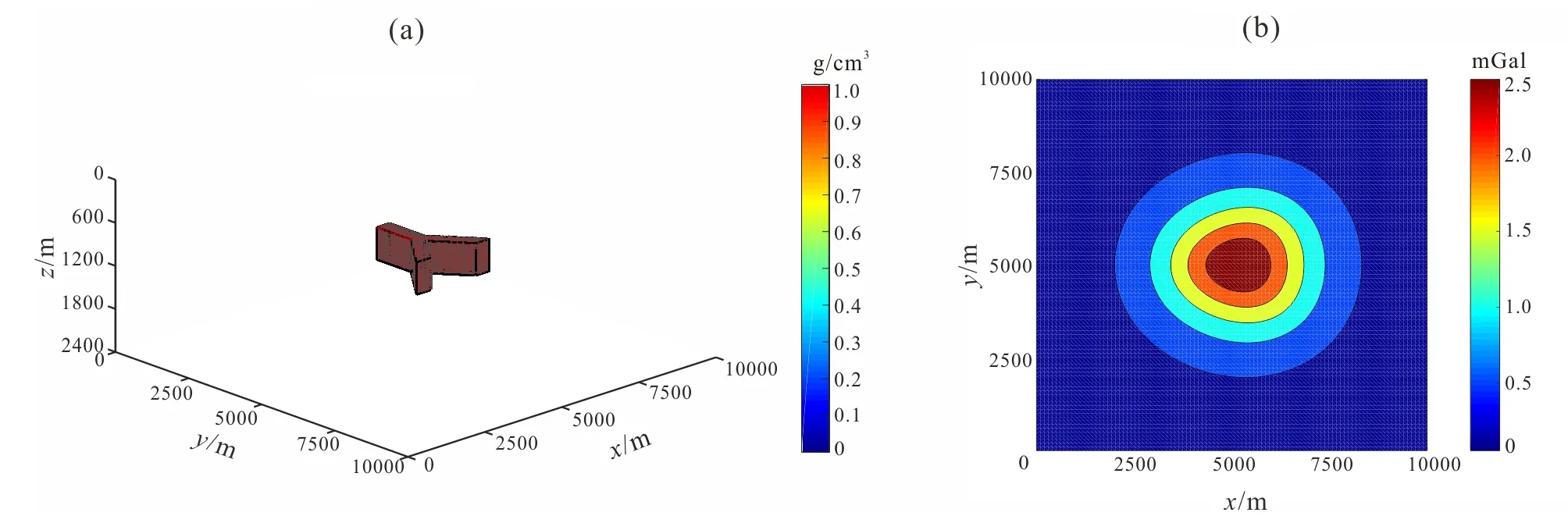
(a) 3-D model; (b) gravity anomalies observed on the ground.Fig.5 3-D model and its gravity anomaly

(a), (d) and (g) show the cross sections of z=900 m for models with 100×100×80 cells, 50×50×40 cells and 25×25×20 cells, respectively; (b), (e) and (h) show the cross sections of y=5000 m for models with 100×100×80 cells, 50×50×40 cells and 25×25×20 cells, respectively; (c), (f) and (i) show the cross sections of x=5000 m for models with 100×100×80 cells, 50×50×40 cells and 25×25×20 cells, respectively.Fig.6 Profiles of inversion results of different model scales

3 Conclusions

The equivalent storage of geometric trellis can significantly reduce memory footprint of the sensitivity matrix and increase the calculation speed, providing the capability to invert large-scale geological models. With the optimized GPU parallel computing program, the model can reach a maximum size of 800×800×800 cells for forward calculation and 300×300×300 cells for inversion. Our focusing inversion based on GPU parallel computing technology can solve the problem of large memory usage and time-consuming calculation when processing and interpreting massive data covering very large area. The horizontal and vertical resolution of the inversion results are greatly improved as the scale of the model increases, which enable us to better distinguish the specific shape of the geological body and clearly outline the boundary. The inversion results reflect more details of complicated geological structures, showing advantage in accurately inverting complex models.