从一位教师的课堂点评反思教师的教学站位

周迎春

[摘  要] 高效课堂是教师精讲点拨，学生静心学习、独立思考，学生间合作探究的有机结合. 新课程理念倡导教师更好地组织学生自主学习、合作探究，学生的学习方式、过程、结果更加自主和开放. 越是学习方式自主、结果开放，教师的指导和点评就更为重要和关键. 教师的课堂指导站位更高，才能实现学生更深层次的学习认知，才能更好地激发学生的学习兴趣，才能更好地浸透学科核心素养.

[关键词] 课堂点评;学习认知;学科核心素养

参加我校青年教师赛课评课，有如下课例：

课题：抛物线中三角形的面积.

教学回顾：

课题引入：同学们，在抛物线背景下探究几何问题是我们学习二次函数的一大难点，为突破这一难点，得先从探究抛物线中最简单的几何图形——三角形说起.今天，我们主要探讨抛物线背景下三角形的面积问题.

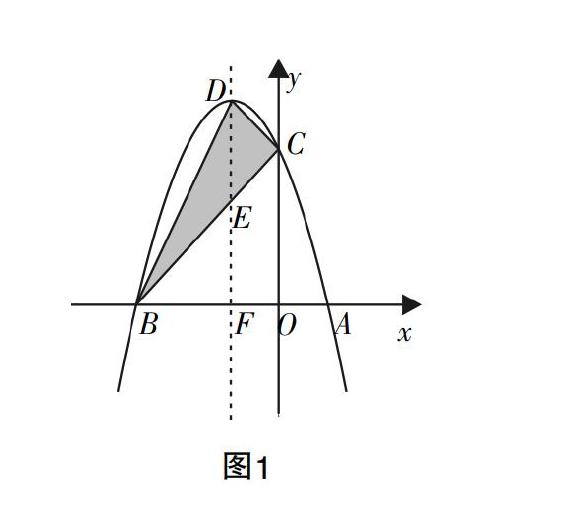
PPT展示例题：如图1，抛物线y=-x2-2x+3与x轴交于A，B两点，与y轴交于点C，抛物线的顶点为D. （展示题目后，教师即引导学生写出四个点的坐标，并将其标注在PPT上）

（1）△ABD的面积为多少？

（2）若点M为抛物线上位于x轴上方一动点，点M在何处时，△ABM的面积最大？最大为多少？

（对有一边落在坐标轴上的三角形的面积，学生很快便解决了）

教师点评：若研究的三角形有一边落在坐标轴上，以此边为底边，将线段的长度转化为点的坐标运算就很容易研究其面积.

探究：（1）△BCD的面积为多少？

教师点拨：以B，C，D为顶点的三角形的面积直接易求吗？△BCD没有边落在坐标轴上，用已有的知识和经验不太好直接处理.那么，能否思考将△BCD的面积通过变形转化为高、底在水平或竖直方向的情形来研究？

学生探究：结合教师的点拨及已有经验，很快便有学生给出了第一种解决方案.

方案一：（如图1）过点D作DE⊥x轴于点F，交BC于点E.

则S△BDC=S△BDE+S△CDE=DE×3.

易知直線BC的方程为y=x+3，

则点E的坐标为E（-1，2），DE=2，

所以S△BDC=3.

教师点评：同学通过点D作x轴的平行线将三角形BCD的面积分割转化成两个底在竖直方向、高在水平方向的三角形面积之和. 结合教师的点评，学生通过思考、小组讨论很快又分别给出了以下几种解决方案.

教师点评：总结以上同学的解题思路，我们不难发现，研究抛物线背景下三角形的面积时常用割补的方法. 可通过作坐标轴的平行线来割补转化，或通过延长边与坐标轴相交来割补转化，也可通过作边的平行线来转化. 对方案七，做题时用得较少，因∠BCD为直角是一种特殊情形，一般不会发生.

探究：（2）若点N为抛物线上位于第二象限内的一动点，那么点N在何处时，△BCN的面积最大？最大为多少？

教师点拨：当点N与点D重合时，面积最大吗？（对比△BCN与△ABM的面积最值，学生很容易发现，当点N与点D重合时，面积不是最大）怎么办？求几何最值有一种常见办法就是函数方法. 那又如何将△BCN的面积表示成函数？表示成哪个变量的函数？

学生探究：

所以当a=-时，△BCN的面积最大，最大值为，此时N点的坐标为N

教师点评：我们研究这种较难的三角形面积最值时，常将面积首先表示为某一变元的函数，然后通过研究函数的最值以达到目的.

方案二：（如图8）平行移动直线BC与抛物线相交，只有一个交点时，以该点作为点N，△BCN的面积最大.

教师点评：这位同学为我们提供了另一种解题思路.

通过平行作等高转化，在平移过程中，显然当直线与抛物线相切时，直线与抛物线在第二象限的交点离BC最远，从而高最大，面积最大.

整节课在教师的启发和问题驱动下，通过学生自主思考、合作探究，呈现了许多好的解法，且没有一个问题和解法是教师直接给予、直接讲授.其次，从学生的参与情况看，教师平常注重对学生的思维训练和能力培养，学生思维活跃，口头表达清晰简洁，学科语言运用准确到位.另外，教师对教学内容及课堂节奏的把控，对学生的组织、调动精准到位. 本节课在赛课中获得了一等奖的好成绩. 但笔者对教师在课堂中的点评站位高度有如下思考和建议.

1. 教师的课堂指导站位更高，才能实现学生更深层次的学习认知

科学与艺术的一个共同美学准则是“境界为先，技术为次”，技巧始终是第二位的. 我们看教师课堂上的这段点评：“总结以上同学的解题思路，我们不难发现，研究抛物线背景下三角形的面积时常用割补的方法. 可通过作坐标轴的平行线来割补转化，或通过延长边与坐标轴相交来割补转化，也可通过作边的平行线来转化.”让学生认知、理解和掌握的更多的是一些解题技巧，教师点评时提到的作坐标轴的平行线、延长边与坐标轴相交或作边的平行线更是小之又小的技巧，它们的目的都是通过等积变换转化成三角形的底和高在水平方向或者竖直方向，让学生在现有认知水平下容易计算底和高而已.笔者以为，研究几何图形的“积”（面积或体积）本质上就是探寻便于计算的底和高，是否需要割补或者运用割补也只是为了实现该目的的一种技巧，割补的主要目的是为了将不规则图形转化为规则图形或是将规则图形作一种等积变换达成更便于计算的底和高. 本题中教师如果站在这样的层面来点评和指导，学生学会的就不仅仅是割补这种解题方法以及解决本节内容的几种常见割补技巧，而是更多感悟和掌握探究几何图形面积的一般思维方式，进而由三角形衍生到其他平面图形，甚至延伸到以后立几中的几何体体积研究. 这样就能实现学生更深层次的学习认知，实现更高远的课堂效益.

2. 教师的课堂指导站位更高，才能更好地渗透学科核心素养的培养

伊思·斯图尔特曾说：“数学的全部力量就在于直觉和严格性巧妙地结合在一起，受控制的精神和富有灵感的逻辑.”受控制的精神和富有灵感的逻辑正是数学的魅力所在，也是数学教育者努力的方向. 当学生直觉感知到BC⊥CD并验证成立时，其他同学发出由衷的赞叹声和掌声，可以看出学生对这种直觉判断的创造性产生的震撼和共鸣. 学生直觉感知到图形的特殊性，这是很有创意的直觉思维！

直观想象是发现和提出问题、分析和解决问题的重要手段，是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础. 当问题研究不易从条件、结论间的联系进行逻辑思考时，通过直觉判断并加以验证，这是一种创造性思维.这时若教师的点评不是“这种方法做题时用得较少，因为∠BCD为直角是一种特殊情形，一般不会发生”，而是因势利导，对学生的大胆设想给予充分肯定，对其合理成分及时鼓励，就能使学生对自己的直觉有成功的体验，强化他们的自信力，从而创生支持欣赏直觉思维的良好环境. 就能更好地实现新课程理念中要求的学生能收集、选择、处理数学信息，做出合理推断和大胆猜想，形成直观想象，再进一步去寻求完善结果的思维方式培养，更好地浸透直观想象的核心素养.

3. 教师的课堂指导站位更高，才能更好地激发和保持学生的学科兴趣

子曰：“知之者不如好之者，好之者不如乐之者.”人们对感兴趣的事物总是不知不觉地心向神往，表现出注意的倾向.而学生的学习兴趣不是天生的，是后天的学习过程中不断培养形成的. 同时，学生对数学产生兴趣的原因常有两种，一种是教师的人格魅力，其二是来自数学本身的魅力. 不可否认情感的重要作用，但兴趣更多来自于数学本身，来自于对数学本质（数学基本概念、数学思想方法、数学思维方式）的感悟和把握.

本节课是一节复习探究课，通过几个问题探究抛物线背景下三角形的面积.学生在探究△BCN的面积最值给出两种解题方案后，教师的课堂点评若不仅是针对两方案本身，而是进一步指出：“同学给出的两种方案恰好就是解决几何最值的两种常见思维方式，一是用函数思想将研究的几何量表示为某变元的函数，通过研究函数的最值（以數助形）达到目的;另一种是用化归思想抓住问题的几何特征，从图形变换角度研究几何最值（以形助数）.”这样，对问题的数学本质诠释就更到位了，学生从中对数学问题的理解就更透彻了，对数学问题的内在规律认识就更深刻了，从而进一步从对问题的理解、认识、解决过程中获得成功的体验，培养学科自信，产生强大的学习钻研动力，更好激发和保持学科兴趣.

新课程理念提倡学生自主探究、合作交流，自主、合作探究学习之后的教师指导和点评就更加重要.只有教师的课堂指导站位更高，学生得到的才不仅是一个个数学概念、解题方法的呈现，而是使学生掌握和感悟到隐含在概念、解法背后的数学思想方法、数学思维方式，从而让学生保持更持久的学习动力，实现更深刻的学习认知，更好地浸透学科核心素养，实现更高远的课堂效益.