高中数学教学中学生运算能力的培养

李军华

[摘  要] 在数学教学中，有几项能力是学生必须要具备的，其中之一便是数学运算能力，这是其他各种能力的基础. 对学生数学能力进行有效的培养，能够在很大程度上使学生的数学水平得到提高. 文章将结合一些相关的资料，分析一下高中数学教学中学生运算能力的培养策略.

[关键词] 高中数学;运算能力;培养策略

数学教学之中的运算能力，主要是指对数或者是对式子，以及对具体数值进行计算或交换的能力[1]. 这样的运算是数学活动的基本形式，也是一种很重要的演绎推理，通过提高这样的能力，能够使得学生的数学学习能力得到促进，而且还能够使学生运用数学知识去解决实际的数学问题. 此外，在促进学生数学思维发展的过程中，教师需要使其能够养成良好的解决问题的习惯，进而使得他们严谨认真的科学精神与态度得到有效的培养. 从这样一些角度来看，在数学教学中对学生的运算能力进行培养，是教师教学中的一项重要任务. 接下来，文章将以高中数学教学内容为例，探讨应该如何在数学教学中对学生的运算能力加以培养.

[?]目前数学运算中存在的主要问题

在目前的高中数学教学中，部分学生的数学运算能力状况是比较差的，这就导致学生的数学水平停滞不前. 出现这样的问题，除了教师在教学上的不合理之外，与学生的不良运算习惯也有很大的关系，具体情况如下：

其一，便是教师教学方式的不合理. 部分教师为了提高学生的运算能力，喜欢采用“题海战术”. 但是在进行运算训练的时候，却没有注意要使其具有针对性，这就导致学生在运算过程中因为重复做题的缘故，使得他们的数学思维受到禁锢，使得他们的思维得不到调动;此外，便是在长久的训练之中，会使得学生产生厌烦心理，从而使得他们不喜欢数学运算.

其二，便是学生在运算之前审题马虎. 对学生解题质量和计算质量造成影响的一个重要原因，便是审题时不认真. 这样一种计算习惯会使得学生在计算的时候马虎大意，经常性的因为一目十行也导致没有看清楚题目目标，从而使得他们在实际运算的时候，出现问题. 而且，这样一种不认真审题的习惯，在高中学生群体中并不是个别存在的.

其三，便是学生在运算过程中出现程序混乱的情况. 在对目前的学生数学运算情况进行分析之后，能够发现学生在运算过程中，因为对数学概念、公式以及原理等运用的不够到位，导致他们在运算过程中显得毫无章法. 因为运算的混乱，导致最终的运算结果出现错误.

其四，便是学生在运算后，没有进行仔细的检查. 学生在运算的过程中，会因为自身的小疏忽而出现计算错误，如果通过后期的检查的话，则可以避免，但是部分高中学生并没有后期检查的习惯，这就导致这样一些错误长期存在.

[?]培养学生数学运算能力有效策略

1. 对学生的思维进行有效性发展

總的来说，提高学生数学运算能力的目的之一便是为了使学生能够有效应对考试，而在目前的高考数学之中，一个最为明显的特点便是“以能力立意命题”，根据这一要求，教师就必须要对学生的运算能力进行培养. 而在培养学生的运算能力的时候，教师需要注意“通性”“通法”的适用性广度[2]，通过对学生的数学思维进行有效的发散，来使得学生能够在学习时更加容易接受，进而使得他们的运算以及推理能力得到提高.

例如，以“圆锥曲线与方程”这个章节的教学内容为例. 其中有这样一个题目，即“已知现在需要过一点（m，0）作圆x2+y2=1的切线，并交椭圆G：+y2=1于A，B两点. 若此时将AB用来表示为m的函数，请求出AB的最大值”. 当学生在运算这个题目的时候，教师需要对学生进行指导，来使得学生的思维能够得到有效的发散. 首先，教师需要使学生结合已学经验明确这样一点，即“切线不能够过圆内的任意一点”，所以可以判断点（m，0）是在圆外，可以判定m≥1. 在经过这样的判定之后，教师可以让学生以小组合作探究的形式，来对此时的“切线的斜率是否存在”的问题进行讨论，最好的方式是进行分类探讨. 即“当斜率存在的时候”，此时使学生注意需要引入参数，并且用m来表示这个参数，进而进行消参. 最终将直线以及椭圆方程有效结合，从而使得能够将AB计算出来. 此外，在进行最值运算的时候，教师可以引导学生采用“基本不等式”“数形结合”或者“导数”的方式来进行运算. 通过这样的引导，来使学生的数学思维得以发散，进而使得他们的运算能力得到提升.

2. 对学生运算求解视野加以开拓

学生学习的积极性有的时候可以通过在运算过程中获取成就感而受到刺激，所以教师在教学过程中，可以通过使学生对一道题目进行多个解答，使学生能够掌握“一题多解”“一题巧解”的能力，来使学生的数学运算视野得到开拓. 使学生能够在解决具体数学问题的过程中，使学生的运算能力以及解题能力得到提高.

例如，以“数列”这个章节的教学内容为例. 在这个章节的教学中，会涉及“等差数列”的学习. 由此，教师可以通过一个等差数列的问题，来培养学生的“一题多解”的思维. 比如，“已知一个等差数列为{an}，其中a1=20，Sn是前n项的和，并且知道S10=S15，请计算，当n为多少的时候，Sn的值最大？”在解答这个问题的时候，教师可以先让学生结合自己的已有经验来对这个题目进行分析，将所有可以想到的答案都列出来，并且一一对应进行计算，最终找到一个最优的解法. 例如，学生可以Sn取最大值时的必备条件来进行解答，想要使Sn的值最大，那么必须要利用等差数列中的基本量，以及取最大值的所具备的条件，即“因为S10=S15，且a1=20，所以根据题意可以列出等式10×20+×d=15×20+×d，在得出d=-后，能够得出当n=12或者n=13的时候，Sn可以取到最大值，即最大值为130”. 出了这样一个计算方式，教师还可以引导学生从“将等差数列前n项和求最大的值的问题向二次函数的最值问题进行转化”，从而得出最大值为130. 其三，教师还可以通过引导学生对等差数列中项的性质加以利用，从而得出a13=0，由此便可以推断出a12>0，进而推断出来Sn有最大值，且有两个. 其四，教师可以引导学生通过对“S10=S15”加以利用，并结合二次函数的性质，将它的对称轴n=12.5求出来，进而确定n为自然数，所以取12或者13，最终求出最值. 通过让学生从不同的角度来对数学题目进行运算，来使得他们的思维得到发散，进而使得他们的运算能力可以在发散思维的过程中得到锻炼.

3. 有效监控学生的数学运算过程

有句话说得好，“细节决定成败”，在进行数学运算的时候，一个小小的失误可能会导致整个运算过程的失败. 所以，在日常教学之中，教师需要对学生的运算过程进行有效的监控，要使学生能够养成良好的运算习惯.

例如，以“函数的基本性质”这个小节的教学为例. 在对与这个小节的内容有关的数学问题进行计算的时候，需要注意这样几点：

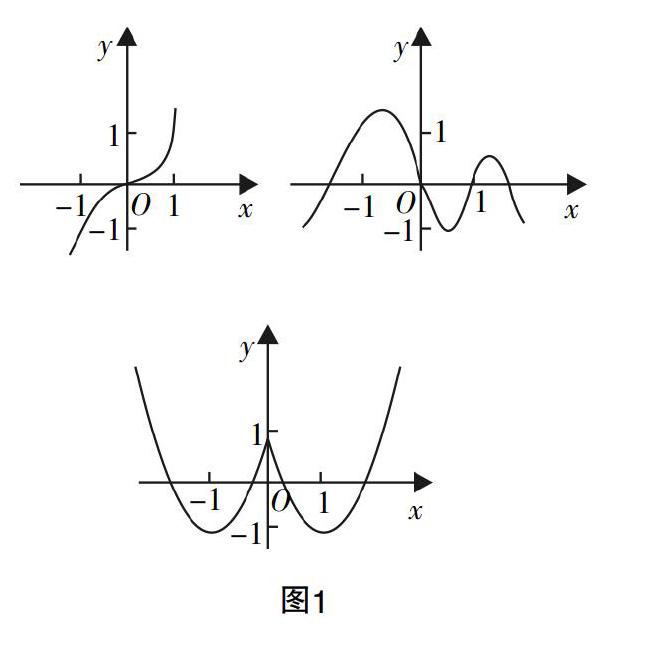
其一，便是需要审题. 教师需要使学生能够养成良好的审题习惯，需要使学生能够从平时的运算过程中就开始注意. 比如说在教学“函数的基本性质”这个小节的知识的时候，需要使学生能够对函数的图像加以把握，在看见函数的时候，通过作出图像，能够判断是何种函数（如图1）.

其次，便是对草稿纸的合理使用. 在计算函数问题的时候，会涉及大量的计算，而学生在计算的过程中，总会因为随意列出计算过程而导致整个草稿纸看起来极为混乱. 这样一种情况，就导致学生在用上一个计算答案进行下一次计算的时候，会因为不小心而出现错误，进而导致最终结果的错误.

其三，学生在进行数学运算的时候，有的章节的计算因为数字的庞大或者是运算过程的复杂，使得学生在笔算的时候产生烦躁心理，而为了避免这种情况的产生，不少教师会建议学生用计算器. 但是计算器的不合理使用，会对学生运算能力的培养产生阻碍效果.

其四，便是要进行算后检查. 在运算完毕后，如果有足够的时间，就一定要进行有效的检查，这能够对学生运算能力的提高提供帮助.

[?]结语

总的来说，为了使学生的数学运算能力得到提高，教师需要对目前影响学生运算能力提高的因素加以分析，从而采用正确的方式来进行解答. 比如说，可以通过对学生的思维进行有效性发展、对学生运算求解视野加以开拓以及有效监控学生的数学运算过程，从而使得学生的运算能力得以提高.

参考文献：

[1]  刘世恒. 浅谈高中数学教学中学生数学运算能力的培养[J]. 关爱明天，2015（6）.

[2]  郭宗雨. 解题需要真功夫——高中数学教学中学生运算求解能力培养的一点认识[J]. 中学数学教学参考：上半月高中，2009（8）.