基于MATLAB的汽车动力性参数的确定
2019-09-17李晓锋
李 静,李晓锋
(郑州工程技术学院 机电与车辆工程学院,河南 郑州 450044)
1 数学模型
汽车在行驶过程中,受到的阻力有滚动阻力、空气阻力、坡度阻力、加速阻力[1],分别用Ff、Fw、Fi、Fj表示,驱动力用Ft表示,可得汽车驱动力阻力平衡方程为
Ft=Ff+Fw+Fi+Fj,
(1)
式(1)的具体化形式为
(2)

1.1 最高车速的计算
最高车速指汽车在水平良好路面上能达到的最高行驶速度[2]。此时坡度阻力和加速阻力均为0,平衡方程式(2)变为
(3)
汽车车速ua与发动机转速n之间的关系为
(4)
发动机转矩Ttq与转速n之间的关系[3]为
Tlq=a0+a1n+a2n2+…+aknk,
(5)
其中系数a0,a1,a2,……ak可由最小二乘法拟合确定,拟合阶数k一般取3或4,本文取4。
由上述关系式可知,平衡方程式(2)可以转化为以车速ua为变量的一元高次方程。
1.2 加速时间的计算
加速时间用来表征汽车的加速能力,可以用原地起步加速时间和超车加速时间来表明汽车的加速能力[4]。原地起步加速时间指汽车由1档或2档起步,以最大的加速度(包括合适的换档时机)逐步换到最高档后,到某一预定的距离或车速所需要的时间(本文指达到最高车速的80%所需要的时间)。超车加速时间指用最高档或次高档由某一较低车速加速至某一高速所需的时间。由驱动力阻力方程(1)(2)可得加速度方程(坡度阻力为0)为
(6)
而t又可以写成积分形式
(7)
假定由低档加速到发动机最高转速时换入高档,对于普通5档变速器,式(7)应分段表示为
(8)
对于装有手动变速器的汽车,因换档时需要切断动力,发动机转速会下降,其下降程度和驾驶员的操纵熟练程度有关。为了描述不同驾驶人操作程度对下降转速的影响,本文引入了档位转速系数,计算公式[5]为
(9)
式中:ngk(k+1)—换入k+1档时的初始转速;ngm(k)—前一档的终止转速。对于换档熟练的驾驶员,β可取0.9~0.95。
1.3 爬坡能力的计算
汽车的爬坡能力用汽车满载(或某一载重质量)时在良好路面上的最大爬坡度来表征[6]。假设汽车匀速爬坡,根据方程(1)(2),可得坡度阻力方程为
Fi=Gsinα=Ft-Ff-Fw,
(10)
可得到α的表达式为
(11)
2 实例分析
以国产某小型轿车为例,利用上述模型,借助MATLAB工具进行仿真输出[7]。
2.1 车辆参数
发动机排量:1096mL;最大转矩:87Nm;转速范围:800~5500r/min;满载质量:970kg;车轮半径:0.272m;传动效率:0.9;空气阻力系数:0.3;迎风面积:2.3m2;滚动阻力系数:0.012;旋转质量换算系数:δ=1.03+0.04ig2;主减速器速比:i0=4.388;变速器速比:ig=[3.416 1.894 1.280 0.914 0.757];汽车轴距:2.335m;质心高度:0.71m;质心至前轴的距离:1.12m;路面实际附着系数φ=0.7。发动机输出转矩特性参数见表1。

表1 发动机外特性参数
2.2 仿真结果
2.2.1 最高车速
表1中数据通过MATLAB曲线拟合得到发动机输出转矩M与转速n之间的关系曲线,如图1所示。把车辆参数代入式(2),通过MATLAB仿真软件可得到汽车驱动力—阻力平衡图,如图2所示。由图2得到该汽车的最高车速(图2中交点)uamax=153.5 km/h。

图1 发动机输出转矩特性
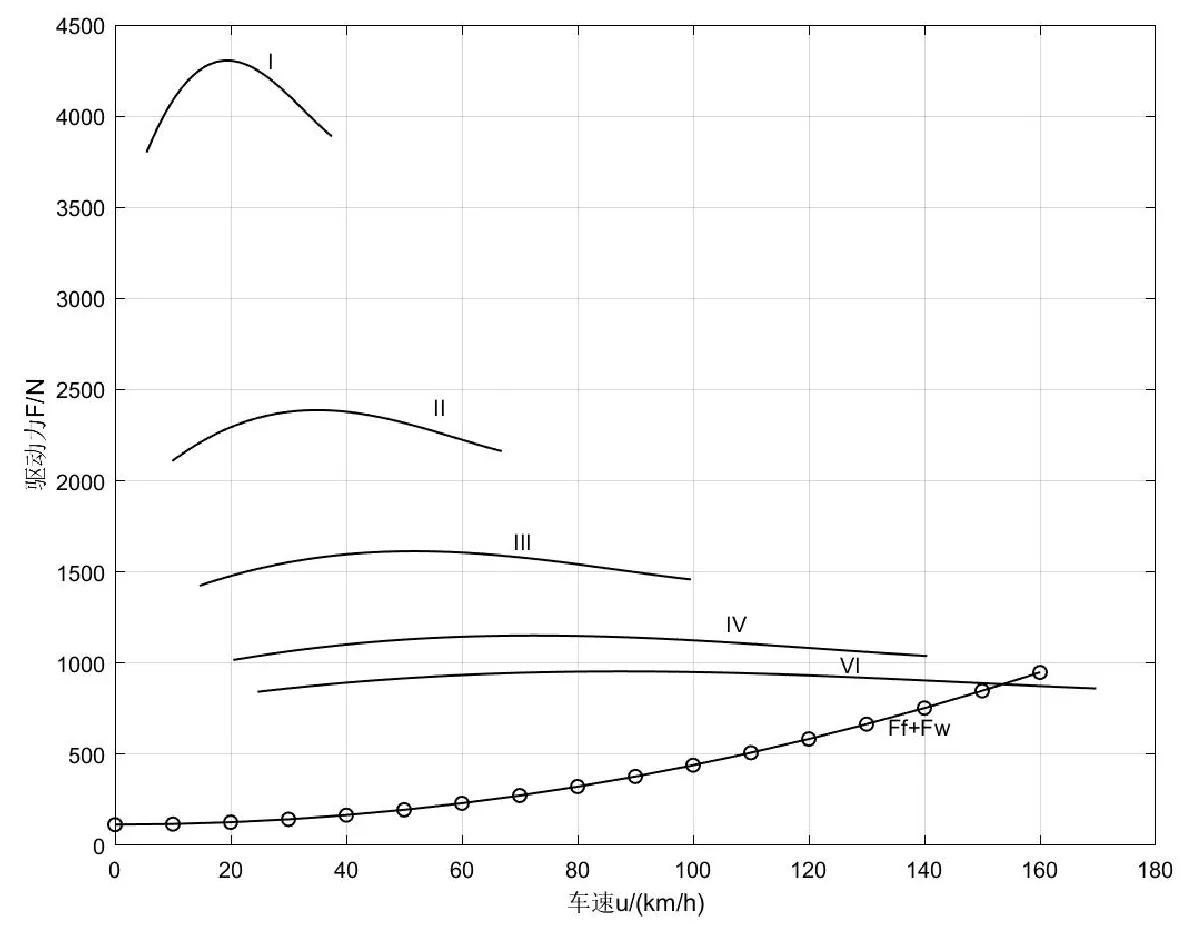
图2 汽车驱动力—阻力平衡图
2.2.2 加速时间
考虑到驾驶员操纵熟练程度这个因素,把档位转速系数β分别设为0.9和0.8,可得到原地起步加速时间、行驶距离与车速之间的关系曲线,分别如图3~图6所示。可以看出驾驶员主观因素对加速时间和行驶距离有一定的影响。在实操中,应选择操纵熟练的驾驶员,并需多次实践,以减小误差[8]。
(1)β=0.9时的输出结果
由图3可得β=0.9时汽车原地起步连续换档(加速至最高车速的0.8)加速时间为40.93 s;由图4可得β=0.9 时汽车原地起步连续换档(加速至最高车速的0.8)行驶距离为972.9 m。

图3 加速时间与车速关系曲线(β=0.9 )

图4 行驶距离与车速关系曲线(β=0.9 )
(2)β=0.8时的输出结果
由图5可得β=0.8时汽车原地起步连续换档(加速至最高车速的0.8)加速时间为46.77 s;由图6可得β=0.8时汽车原地起步连续换档(加速至最高车速的0.8)行驶距离为1091.6 m。
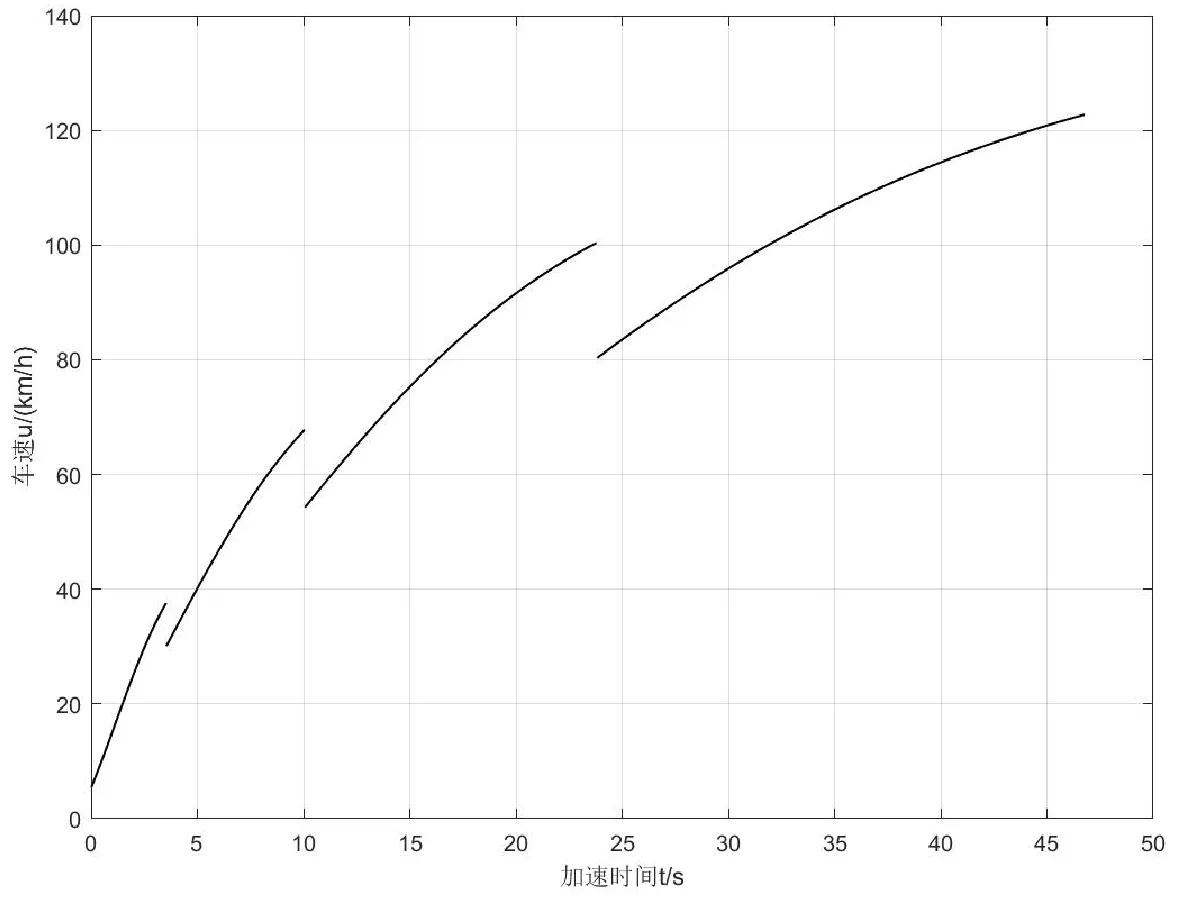
图5 加速时间与车速关系曲线(β=0.8 )

图6 行驶距离与车速关系曲线(β=0.8 )
2.2.3 最大爬坡度
通过仿真输出得到该车辆爬坡度图,如图7所示,可以看出该车辆的最大爬坡度为I档爬坡度0.481,所需要的路面附着系数为1.29。一般来讲,干燥、良好的沥青或混凝土附着系数为0.7~0.8,路面附着系数大于此值时,0.481的爬坡度不会实现。因此,本文对实际的等效坡度进行了计算,假设该车为前驱车辆,路面附着系数为0.7,得到的实际最大爬坡度为0.3。

图7 汽车爬坡度图
1档的最大爬坡度为0.481,最大坡度角为25.69 度,前驱汽车匀速上坡时要求的附着系数为1.29。上述情况超过路面实际附着系数0.7,重新计算,得汽车能通过的实际最大坡度为0.30,汽车能通过的实际最大坡度角为16.72度。
2.3 手动变速箱和装有液力变矩器车辆的动力性比较
目前汽车上广泛使用的无级变速器是液力变矩器,通过发动机和液力变矩器的共同输入,使车辆既能充分利用发动机的最大有效功率,又尽可能工作在发动机比燃料消耗量最低值附近。本部分涉及的计算公式本文没有给出,仅由图8、图9进行简要说明。
从图8可以看出,在初使速度为0时,装备液力变矩器和5档变速器的汽车(实线)就能连续发出很大的驱动力,比装备手动变速器(虚线)的1档驱动力要大很多,这是配备液力变矩器车辆起步平稳、加速较好的原因。但是随着车速的提高,其驱动力下降要比手动变速器车辆快得多,为了解决这一问题,现代车辆采用了带锁上方式的液力变矩器,如图9所示,提高了液力变矩器的传动效率,使车辆的动力性与燃油经济性都得到了提高。
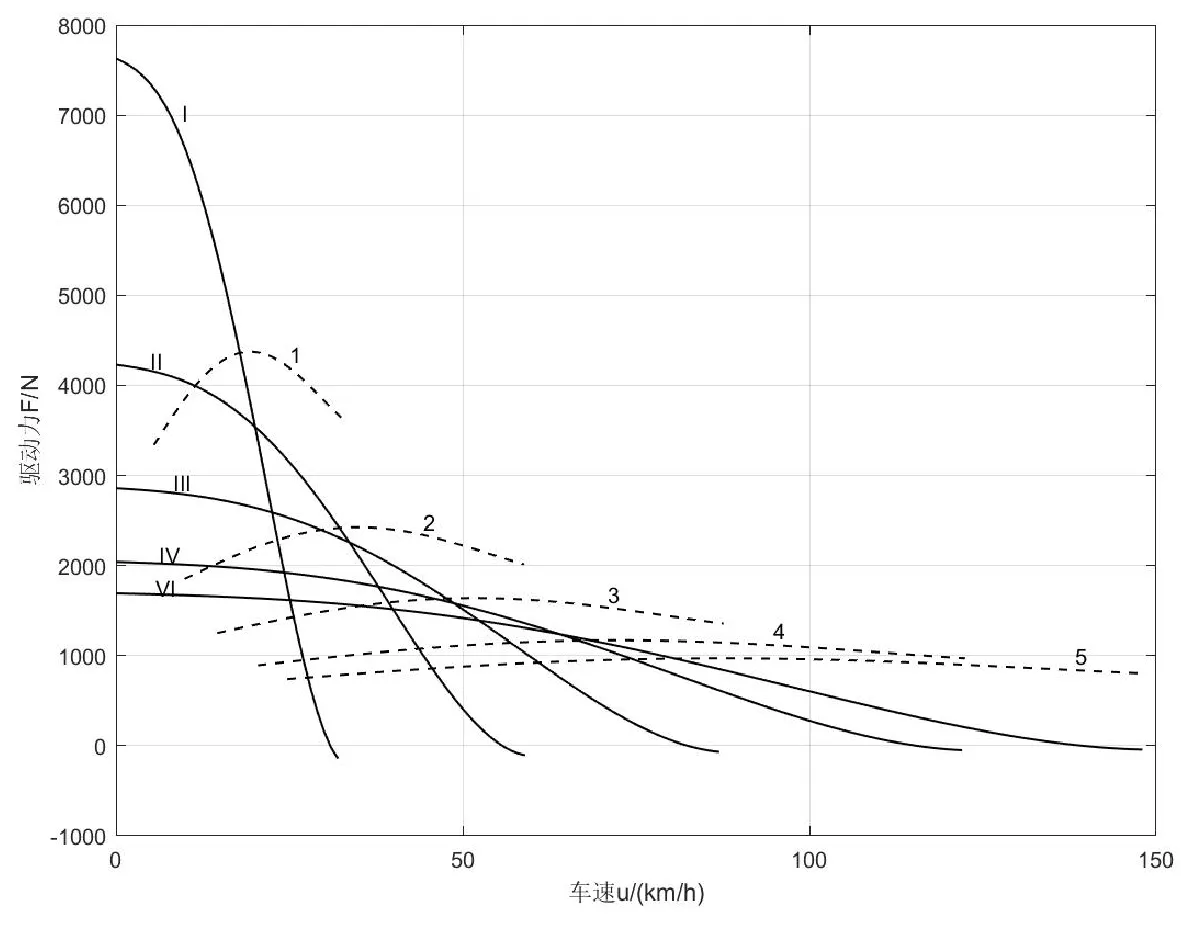
图8 装备液力变矩器与装备手动变速器的驱动力对比

图9 采用锁止液力变矩器与装备手动变速器的驱动力对比
3 结论
通过对上述实例进行分析计算,得出以下结论:
(1)该车的最高车速uamax=153.5 km/h;
(2)在计算加速时间的过程中,引入档位转速系数来评价驾驶员的熟练程度这一主观因素,可得到0~122.8km/h的加速时间为40.93s(β=0.9)、46.77s(β=0.8)。
(3)该车的理论最大爬坡度imax=0.481,超出了路面的附着力。按实际路面附着系数φ=0.7重新计算,得到该车1档的最大爬坡度imax=0.30。
(4)配备有锁止液力变矩器无级变速器的车辆与手动变速箱车辆相比,因其 传动系机械效率的提高,使得车辆的动力性、经济性都有所提高。
