弱单投射半模

曾慧平，张传美，刘浩广

(南昌航空大学 科技学院，江西 南昌 330034)

在对半环理论的半模研究工作中，国内外专家学者都尝试用模论的研究方法，将模的性质推广到半模中.但受半环与半模自身的条件限制及半模与模差异的制约，推广工作并不顺利.文献[1-3]研究了条件较弱的投射半模，如投射半模、k-投射半模和平坦半模.此外，如伪k-投射半模[4]、拟主k-投射半模[5]、伪投射半模[6]等一系列关于投射半模的研究都试图保留环上投射模的较好性质,这些研究成果极大地推动了半模理论的发展.论文进一步放宽投射半模的条件，引入弱投射半模的概念，尽可能地保留了投射模中的相关结论，研究了弱单投射半模的同调性质.证得：若P是正则半模，则P是弱拟单投射半模当且仅当P是投射半模.此外，论文还定义了弱拟单投射半模，给出完全可减、加法可消半环R上弱拟单投射半模的两个等价条件.

定义1[1]对给定的半模P，若g:M→N是任意半模满同态，对任意半模同态f:P→N，存在同态h:P→M，使得gh=f，则称P是投射半模.

定义2[1]设f:M→N是半模同态，记Kerf={m∈M|f(m)=0}，f(M)= {f(m)|m∈M}，Imf={n∈N|n+f(m)=f(m′),∃m,m′∈M}.若Imf=f(M)，则称f是i-正则的；若对m,m′∈M,满足f(m)=f(m′)，必存在k,k′∈Kerf，使得m+k=m′+k′，则称f是k-正则的．

若序列

(1)

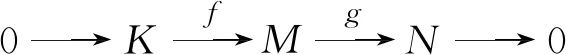
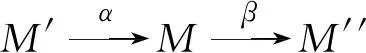
图1 非水平同态交换图

定义3[7]称左R-半模M的子半模N是可减的当且仅当若m+m′∈N，其中m∈N，则有m′∈N,∀m,m′∈M.称M是完全可减半模若M的任意子半模都可减．文中其他未提及的概念同文献[1-12]一致.

1 弱单投射半模

定义4[7]设N是M的子半模，若N只有平凡子半模，则称N是M的单子半模.

定义5设g:M→A是半模同态，若Kerg是M的可减单子半模，则称g是饱和同态.

定义6对给定的半模M、P，若任意k-正则饱和满同态g:M→N及半模同态h:P→N，存在同态γ:P→M，使得gγ=h，则称P是相对M的弱单投射半模，也可称P是M-弱单投射的.若对任意半模M，P是M-弱单投射的，则称P是弱单投射半模.

定理2已知M和P均为半模，则下列论述等价：

(1)P是M-弱单投射的；

也是短真正合列，其中f是i-正则单同态，g是k-正则饱和满同态，g*(α)=gα；

(3)L是半模M的任意可减单子半模,对任意同态α∈HomR(P,M/L)，存在γ∈HomR(P,M)，满足α=πγ，其中π是自然满同态.

(3) ⟹(1).设g:M→N是k-正则饱和满同态.∀f∈HomR(P,N) ，取L=Kerg及自然满射π:M→M/L，显然π也是k-正则饱和满同态.由文献[8]中推论2知，存在半模同构h:N→M/L，使得π=hg.取hf:P→M/L，由(3)知，存在γ:P→M,使得hf=πγ=hgγ，即f=gγ.证毕.

推论1已知P为半模，则下列论述等价：

(1)P是弱单投射半模；

也是短真正合列，其中f是i-正则单同态，g是k-正则饱和满同态，g*(α)=αg；

(3)M是任意半模且N是M的任意可减子半模，对任意同态α:P→M/L，存在h∈HomR(P,M),满足α=πh.

定理3若N是A-弱单投射的，B为A的可减子半模，则N是B-弱单投射的.

证明设X是B的任意可减单子半模，任意半模同态f:N→B/X.图2为可减半模交换图.如图2所示，记π1，π2是自然满同态，i1，i2是自然单同态，i2π1=π2i1显然成立.因为N是A-弱单投射的，故存在h:N→A，满足i2f=π2h.∀n∈N，因为π1为满同态，故存在b∈B，使得π1(b)=f(n)，有

π2h(n)=i2f(n)=i2π1(b)=π2i1(b).

(*)

定理4设(Pk)k∈Λ为半模族，则⊕k∈ΛPk是M-弱单投射的当且仅当Pk(∀k∈Λ)是M-弱单投射的(证明过程同文献[7]一致).

推论2(Pk)k∈Λ为半模族，则⊕k∈ΛPk是弱单投射的当且仅当Pk(∀k∈Λ)是弱单投射的.

定理5已知P是投射半模.若P的商半模均是内射的，则P的任意子半模是P-弱单投射的.

证明设K是P的任意子半模.图3为商半模交换图.如图3所示，i，π分别表示自然单射和自然满射，X是P的任意可减单子半模.∀f∈HomR(K,P/X)，因P/X是内射的，则有γ∈HomR(P,P/X)，满足f=γi.又因P是投射的，故存在h∈EndR(P)，满足γ=πh，即有f=γi=πhi.取g=hi:K→P，可得K是P-弱单投射的.

图2 可减半模交换图 图3 商半模交换图

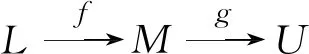
也是真正合列.

是短真正合列.

定义η:M/Kerg→U为η(m/Kerg)=g(m).若η(m1/Kerg)=η(m2/Kerg)，则g(m1) =g(m2).因g是k-正则同态，故m1+k1=m2+k2，∃k1、k2∈Kerg，有m1/Kerg=m2/Kerg，即得η是单同态.图4为同调非水平交换图.

图4 同调非水平交换图

现考虑图4,其中φ*(ξ)=φξ，η*(γ)=ηγ，ξ∈HomR(P,L),γ∈HomR(P,M/Kerg).若η*(ζ)=η*(γ)，ζ,γ∈HomR(P,M/Kerg)，即ηζ=ηγ.由η是单同态可得ζ=γ，即η*也是单同态，得非水平序列

是真正合列.

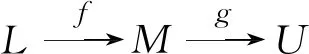
综上所述，由定理1可得，序列

是真正合列.

定义7称P是wk-正则的，若存在一个自由半模F和k-正则饱和满同态f:F→P.显然wk-正则半模必是k-正则半模.

定理7设P是wk-正则的，下列论述等价：

(1)P是弱单投射的半模；

(2)P是投射半模.

(2)⟹(1).显然成立.

2 弱拟单投射半模

定义8若P是相对P的弱单投射半模，则称P是弱拟单投射半模.

引理1[9]若R是完全可减半环，则R的任意非零自由半模F是完全可减的且任意k-正则半模是完全可减的.反之，若非零自由半模F是完全可减的，则R是完全可减的.

定理9设R是加法可消、完全可减半环，P是wk-正则的，则下列等价：

(1)P是弱拟单投射的；

(3) 存在自由半模F与半模K，满足F≅K⊕P.

证明(1)⟹(2).由引理1直接可得.

若η(m,p)=η(m1,p1)，即m+γ(p)=m1+γ(p1)，则有β(m)+βγ(p)=βm1+βγ(p1)，可得βγ(p)=βγ(p1).又由βγ=IP，可得p=p1，即m+γ(p)=m1+γ(p).由于R是加法可消半环，由文献[9]中定理1.11可知，F也是加法可消，因此m=m1.证得η是单的.

∀a∈F，则βη(0,β(a))=β(0+γβ(a))=βγ(β(a))=β(a).由于β是k-正则的，则a+m1=η(0,β(a))+m2，其中m1,m2∈M=Kerβ，显然有a+η(m1,0)=η(0,β(a))+η(m2,0).因为R是完全可减的，故F也是完全可减的，从而η(M⊕P)是可减的，可知a∈η(M⊕P)，即证η是满同态.证得η是同构.

(3)⟹(1). 设α:F≅K⊕P→P是合成同态，其中第二个映射是自然投射，β:P→K⊕P≅F是合成同态，其中第一个映 射是自然入射.图5为自由半模交换图.如图5所示，对任意k-正则饱和满同态f:P→M及任意同态g:P→M，由于F是投射半模，显然也是弱单投射半模，因此存在γ1:F→P，使得fγ1=gα.取γ=γ1β:P→P，则有fγ=fγ1β=(gα)β=gIP=g，故P是弱拟单投射半模.证毕.

图5 自由半模交换图