基于可变模糊集的电能质量评估方法

张 可，朱唯韦，程志友，凡远柱

(1.南瑞集团有限公司，江苏 南京 211000；2.安徽南瑞继远电网技术有限公司，安徽 合肥 230088；3.安徽大学 教育部电能质量研究中心，安徽 合肥 230601)

电能作为一种使用广泛的能源，其应用程度已成为一个国家发展水平的主要标志之一[1].电能质量问题已引起电网运行部门、电能质量监测设备制造商、监督部门及电力用户的高度重视[2].大型用电设备的使用，对电网的安全运行产生较大影响，因此准确评估大型用电设备运行对电能质量的影响，对电网电能质量的管理有重要意义[3-4].

世界各国先后制定了一系列电能质量国家标准，然而这些标准只能用来判断单项电能质量指标是否合格，不能判断综合电能质量的优劣[5]，因此提出科学、客观的电能质量综合评估方法尤为重要.相关科研人员进行了探索，如文献[6]提出一种排序稳定的电能质量评估方法，引入联系度概念，解决了电能质量综合评估指标的不确定性问题，但联系度系数的确定具有一定的主观性.文献[7]提出一种基于脉冲耦合神经网络(pulse coupled neural networks, 简称PCNN)的电能质量评估新方法.由于电能质量的评估指标由定性和定量指标构成，具有一定的模糊性，电能级别之间也存在模糊性，因此模糊集原理在电能质量综合评估中得到广泛应用[8-9].文献[10]采用的模糊综合评估法一定程度上解决了多指标的综合评估问题，但最大隶属度原则掩盖了评估指标介于两个隶属度之间时可能出现的判断偏差.

笔者提出基于可变模糊集的电能质量综合评估方法，根据轧机系统运行状况确定影响轧机系统电能质量的重要评估指标，对各评估指标赋权时，为避免指标的赋权过于主观或客观，采用最优组合权重法为指标赋权，利用可变模糊集原理对轧机系统3种工况的电能质量进行综合评估，改进了评估级别边界的动态性和模糊性.采用相对隶属度原则替代传统的最大隶属度原则，克服了最大隶属度原则掩盖评估指标介于两个隶属度之间时造成判断结果出现偏差的不足.

1 评估指标体系的构建

电能质量评估是基于系统电气参数的实际测量值或通过建模仿真获得的数据，对电能质量各项性能指标做出评估，且判断其是否满足国家标准的过程[11].单个指标的合格与否并不能体现系统的整体状况，电能质量评估是一个多指标的综合评估.因此，评估指标的选取，对电能质量的评估有着重要影响.笔者结合电能质量国家标准及轧机系统的实际运行状况，选取其中6项稳态指标作为评估指标，如图1所示.

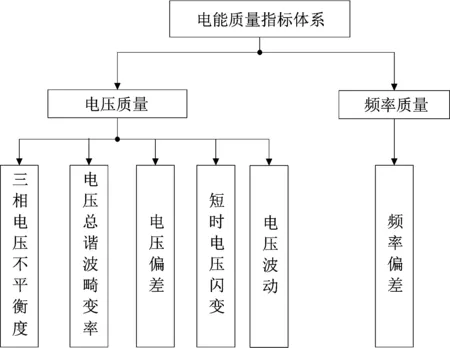
图1 电能质量指标体系

该评估指标体系中选取的6项电能质量指标为：三相电压不平衡度Xεu、电压总谐波畸变率XTHDu、电压偏差Xeu、短时电压闪变XPst、电压波动XΔdu、频率绝对偏差Xf.根据国家标准及专家经验，将指标的限值分为6个级别，如表1所示.为使所有评估数据均包含于对应的级别区间，将指标的边界6扩大至国家标准的两倍，同时定义边界0与边界1间为特优质、边界1与边界2间为优质、边界2与边界3间为良好、边界3与边界4间为中等、边界4与边界5间为合格、边界5与边界6间为不合格.

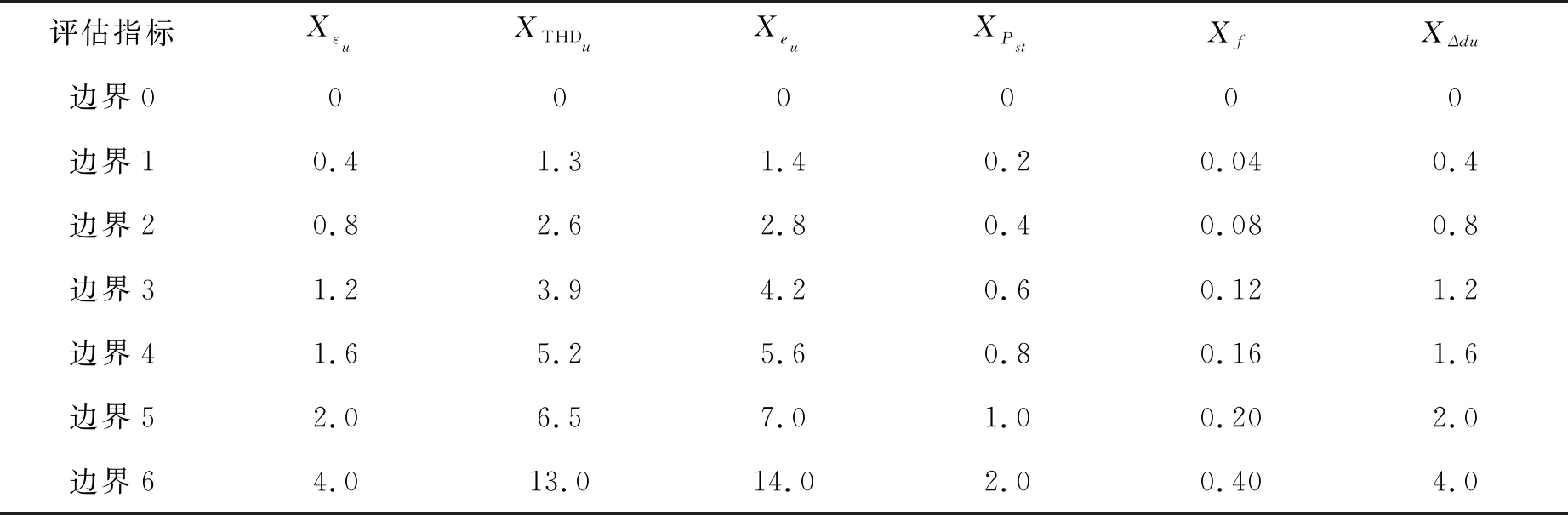
表1 评估指标边界值 %

2 最优组合权重法

电能质量的综合评估[12]过程中，由于不同指标在系统中的重要性不同，综合评估之前，需要对每个评估指标进行权重确定，以提高评估结果的合理性.为了避免赋权时各指标权重过于主观或客观，该文采用最优组合权重法[13]，在主客观权重的基础上计算各指标的最优组合权重.首先采用层次分析法[14]计算各指标的主观权重，然后利用熵值法[15]计算各指标的客观权重，最后通过最优组合权重法计算各评估指标的最优组合权重.

2.1 层次分析法

层次分析法(analytical hierarchy process, 简称AHP)的步骤如下：

(1) 确定评估对象，构造评估指标的判断矩阵.根据1～9标度原则，构造的判断矩阵为

V=(vij)m×n,

其中：vij为判断矩阵标度值，表示指标i相对指标j的重要性.判断矩阵标度值含义见表2.

表2 判断矩阵标度值含义

(2) 对判断矩阵进行一致性检验.判断矩阵的随机一致性比例为

(1)

其中：RI为随机一致性指标，λmax为判断矩阵的最大特征根.当CR<0.1时，认为判断矩阵满足一致性要求，否则修改判断矩阵，直至满足CR<0.1.随机一致性指标的取值见表3.

表3 随机一致性指标的取值

(3) 将判断矩阵的最大特征值对应的特征向量作为各指标的权重系数.

2.2 熵值法

熵值法的基本思想是根据各个指标所包含信息量的大小确定权重.熵值法的步骤如下：

(1) 计算得到的第j项评估指标的熵值为

(2)

(2) 计算得到的第j项评估指标的权重值为

(3)

其中：ej为第j项指标的熵值.

2.3 最优组合权重法

最优组合权重法是在多属性决策条件下，对两种或两种以上单一模型确定的权重进行协调，获得最优权重的优化方法.为了使各指标的权重既结合主观经验又联系客观实际，该文引入偏差函数，使指标权重偏差最小.构造的单目标优化模型为

(4)

其中：wjk为第k个指标的第j种赋权法权重；vki为第k个指标的第i种赋权法的权重；αj,αi分别为第j,i种赋权法的权重系数.利用拉格朗日常数法，可得到各指标的最优权重向量为W=(w1w2…wn).

3 基于可变模糊集的电能质量评估方法

利用可变模糊集原理[16-17]对电能质量进行综合评估.

样本的特征值矩阵为

(5)

其中：xij表示第i个指标第j个时刻的样本特征值.i=1,2,…,m；j=1,2,…,n.

(1) 标准值区间矩阵

设评估指标分为L个级别区间，则m个指标构成的L个级别的标准值区间矩阵为

(6)

其中：i=1,2,…,n;h=1,2,…,L.根据电能质量国家标准并结合轧机系统电能质量实际情况，规定1级为最优状态、L级为最差状态.

(2) 可变范围评估区间矩阵

根据评估指标的标准值区间矩阵Yab,建立评判级别的可变范围评估区间矩阵Ycd.指标i的区间根据矩阵Yab的指标标准值区间及相邻区间确定，据此得到的可变范围评估区间矩阵为

(7)

其中

(8)

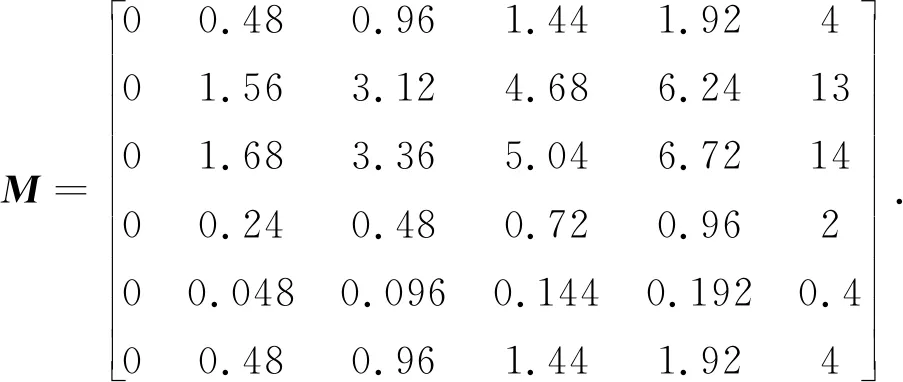
(3) 区间[aih,bih]中相对隶属度等于1的点值矩阵M

联系实际情况，根据矩阵Yab得区间[aih,bih]中相对隶属度等于1的点值矩阵为

(9)

其中

(10)

Mih须满足以下边界条件

(11)

(4) 指标xij在不同级别中的相对隶属度矩阵

设xij为评估指标集内的一个任意值.将xij与第i个指标在不同级别中相对隶属度等于1的点值矩阵元素Mih比较，若xij在Mih左侧，则其相对隶属度模型为

(12)

若xij在Mih右侧，则其相对隶属度模型为

(13)

由式(6)～(13)可得评估指标在不同级别中的相对隶属度矩阵为

(14)

(5) 综合隶属度

第j个时刻的电能质量状态对级别h的综合隶属度为

(15)

其中：wi为指标权重；α为优化标准参数，α=1为最小一乘方准则，α=2 为最小二乘方准则；p为距离参数，p=1为海明距离，p=2为欧式距离.

α,p有4种组合：α=1,p=1；α=1,p=2；α=2,p=1；α=2,p=2.

根据4种组合，计算得非归一化的综合隶属度矩阵为

U′=(jμ′h).

(16)

对上式进行归一化，可得指标i对级别h的综合隶属度矩阵为

U*=(μh)，

(17)

根据文献[18]的级别特征值公式，可得级别特征值向量为

H=(1 2 …L)U*.

(18)

根据上式的计算结果，可对评估指标进行综合定量分析，进而确定电能质量级别.

4 案例分析

选用某钢铁厂10 kV段轧机系统作实验对象.选择三相电压不平衡度Xεu、电压总谐波畸变率XTHDu、电压偏差Xeu、短时电压闪变XPst、频率绝对偏差Xf、电压波动XΔdu为电能质量评估指标，使用电能质量检测分析仪对1周内轧机系统的3种工况(轧机待机、轧机低速轧制、轧机高速轧制)的评估指标进行观测和记录，将测量数据的95%概率大值作为数据典型值.1周内不同工况的测量数据典型值如表4所示.

表4 3种工况的实测数据典型值 %

基于专家经验可得各指标的相对重要性为:电压偏差>电压总谐波畸变率>电压闪变>电压波动>三相电压不平衡度>频率偏差.

使用层次分析法，计算得到的各评估指标的主观权重为

w1=(0.102 5,0.212,0.331 7,0.157,0.087 5,0.109 3).

使用式(2)～(3)，计算得到的各指标的客观权重为

w2=(0.394 6,0.104 7,0.240 6,0.102 4,0.037 7,0.12).

使用式(4)，计算得到的各指标的最优组合权重为

W=(0.190 3,0.179 8,0.304,0.141,0.072 3,0.113).

由表1，4，计算得到的评估样本的特征值矩阵X及指标标准区间矩阵Yab分别为

由指标标准区间矩阵Yab及式(7)～(8)，计算得到的可变范围评估区间矩阵Ycd为

由式(9)～(11)，计算得到的标准值区间矩阵Yab级别区间中相对隶属度等于1的点值矩阵M为

通过1周内轧机系统测量样本的特征值矩阵及式(12)～(14)计算3种工况样本的相对隶属度，然后根据式(15)～(16)计算样本i对级别h的综合隶属度，最后使用式(17)对综合隶属度进行归一化处理，得到不同参数条件下样本i对级别h的综合隶属度矩阵如下：

α=1，p=1时

α=1,p=2时

α=2,p=1时

α=2，p=2时

根据式(18)计算得到的4种参数组合下轧机系统待机、低速轧制、高速轧制3种工况的级别特征值及电能质量综合评估级别(见表5).

表5 3种工况的级别特征值及电能质量综合评估级别

当级别特征值大于相邻两级别特征值的中点值时，取大级别值作为最终的评估级别; 反之，取小级别值为最终评估级别.由表5可知，4种参数组合下轧机系统待机、低速轧制、高速轧制的电能质量级别分别为II级、III级、IV级，因此轧机系统虽为大负荷系统但对电能质量的影响并不大，相对待机和低速轧制工况，高速轧制对电能质量的影响较大.这是因为高速运行时电流较大，导致电压降较大，进而导致电力指标与其标准值之间的偏差较大，对电能质量的影响也会较大.综上可知该文方法具有可行性.

5 结束语

笔者利用最优组合权重法在主客观权重的基础上为各指标赋值，并通过可变模糊集原理对轧机系统不同工况下的电能质量进行综合评估.在可变模糊集原理中，利用相对隶属度代替了传统的最大隶属度，改进了评估边界的动态性和模糊性，克服了最大隶属度造成的当评估值处于两个隶属度之间时出现判断偏差的不足.针对轧机系统的综合评估，可变模糊集原理能够更有效处理相邻评估级别间的模糊性问题，某钢铁厂10 kV段轧机系统电能质量的评估结果表明该方法具有可行性.