相干光OFDM/OQAM 通信系统中的理论和算法设计∗

索珠峰 张 磊 方 熙 高献伟

北京电子科技学院，北京市 100070

引言

正交频分复用/交错正交幅度调制( Orthogonal Frequency Division Multiplexing/Offset Quadrature Amplitude Modulation，OFDM/OQAM)作为下一代通信系统物理层备选波形技术，引起了国内外学者的广泛关注[1-6]。 与4G物理层波形OFDM 技术相比，OFDM/OQAM 用特殊设计的滤波器代替循环前缀(Cyclic Prefix，CP)从而大大提高了频谱效率，通过对原型滤波器的优化系统取得了良好的带外抑制效果，这两方面作用使数字信号长距离高速率的有效传输成为可能[7-10]。 从未来通信应用的场景来看，通信技术需要满足高速率，低延迟，海量连接的需求，同时还不得不面临频谱资源极度紧张的环境[11]。 OFDM/OQAM 具备的很多特性满足了未来应用场景下对于通信技术的需求，如良好的带外抑制，极高的频谱效率，不需要载波同步，适合于零散化的碎片频谱利用等[12-13]。

由于放宽了正交条件，OFDM/OQAM 信号通过非理想信道时会面临严重的固有虚部串扰(Intrinsic Imaginary Interference， IMI)影响从而降低系统鲁棒性[14-16]。 在OFDM/OQAM 系统中选择理想的原型滤波器和有效的信道估计模型可以提升系统的传输性能。 文献[17]在无线系统中研究了高斯滤波器的能量分布。 文献[18]弥补了高斯函数滤波器不能构造正交基而造成的漏磁特性，并提出了各向同性正交变换算法 ( Isotropic Orthogonal Transfer Algorithm，IOTA)。 文献[19]利用高斯函数和IOTA 模型构造了一组扩展高斯函数滤波器(Extend Gaussian Function， EGF)旨在提高时频聚焦特性(Time-Frequency Localization， TFL)。 文献[20]在无线信道中系统地研究了基于前置导频的信道估计模型，提出了伪导频(Pseudo Pilot)概念并设计了一种基于实数序列的IAM-R 模型。

最近，随着城域光通信网的迅速全面布局，光OFDM/OQAM 引起了国内外学者的广泛关注。 文献[15]在一个偏振方向的光OFDM/OQAM 系统中推导了信道估计的一般准则。 文献[21]分析了相干光OFDM/OQAM 系统下的TFL 特性与滤波器选取，然而并没有分析提升信道估计的方法。 文献[22]基于文献[20]中的伪导频概念设计了一种相位偏移(PHO)模型，与传统的IAM-R 模型相比虽然一定程度上提高了系统传输的稳定性，但是该种导频结构由于只用了一列前导序列并不能实现理想的误码率性能。

本文在相干光通信系统中从理论上分析了OFDM/OQAM 信号的传输过程，并介绍了三种常用滤波器(Gaussian、EGF 和IOTA)的适用场景以及三种信道估计模型(IAM-R、PHO 和EPHO)的算法设计。 通过理论描述和仿真验证显示，IOTA 滤波器可以实现较好的时频聚焦特性，EGF 滤波器通过方向参数可以改变时间或者频率方向上的能量聚焦特性，从而弥补某一方向上的噪声抑制能力的不足。 对于信道估计模型，本文提出的E-PHO 通过充分利用前置导频空间，取得了相比于IAM-R 模型与PHO 模型更好的误码率性能和信道传输性能。

1 CO-OFDM/OQAM 基础理论

CO-OFDM/OQAM 系统信号处理流程图如图1 所示，二进制比特流经过信号源送入OFDM/OQAM 发射机准备调制，常用的调制方式为M-QAM 调制，如4-QAM，16-QAM，64-QAM等。 与传统的OFDM 不同的是，OFDM/OQAM使用OQAM 对信号进行调制，具体操作为MQAM 调制后的信号实虚分开，并在时间上半周期错位，这样传输过程中的信号在时域上都为实数信号。 随后对实信号进行基带相位调制、IFFT和原型滤波器滤波器操作。 数模转换器和低通滤波器分别实现数模转换和波形成型。 接收端是发射端的逆过程，低通滤波和模数转换分别实现滤除带外噪声和模数转换功能。 原型滤波、FFT 和相位解调之后进行信道估计和均衡。 均衡后的信号OQAM 解调后进行判决操作，与发射端二进制信源产生的数据对比，计算整个系统误码率，并以此书记作为评价系统优劣的重要指标之一。

根据CO-OFDM/OQAM 系统传输框图，发射端的信号传输方程可以写作:

信号经过色散信道之后面临严重的衰弱，此时接收端信号可以表示为:

对于OFDM/OQAM 系统，原型滤波器的长度是用于调制和解调的快速傅里叶变换(FFT)和逆FFT(IFFT)长度的几倍。 因此，记忆信道长度l 实际上短于原型滤波器的长度。 根据这个结论，下面公式总是成立:

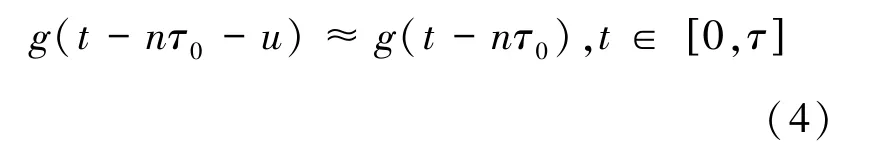
根据公式(4)，公式(3)可以重写如下:

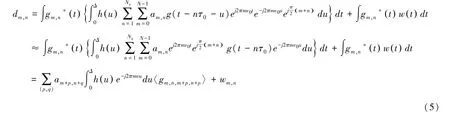
2 CO-OFDM/OQAM 算法设计

2.1 正交性实现

对于使用多载波调制的通信系统而言，子载波间的正交性是信号能够正确解调的基础，OFDM/OQAM 的正交性是靠原型滤波器保证的。 OFDM/OQAM 系统使用的原型滤波函数具备时频聚焦特性，应用于每个子载波的滤波器可以看作原型滤波器的gm，n(t) 频率移位。 滤波器组示意图如下:

图2 OFDM/OQAM 滤波器组(K＝5)

显然，根据图 我们可以看出各子载波之间的重叠仅存在于相邻子载波之间，子载波的奇数部分或者偶数部分无重叠，因此OFDM/OQAM的正交性只考虑相邻子载波即可。 基函数gm，n(t) 的离散域正交性可以表示为:

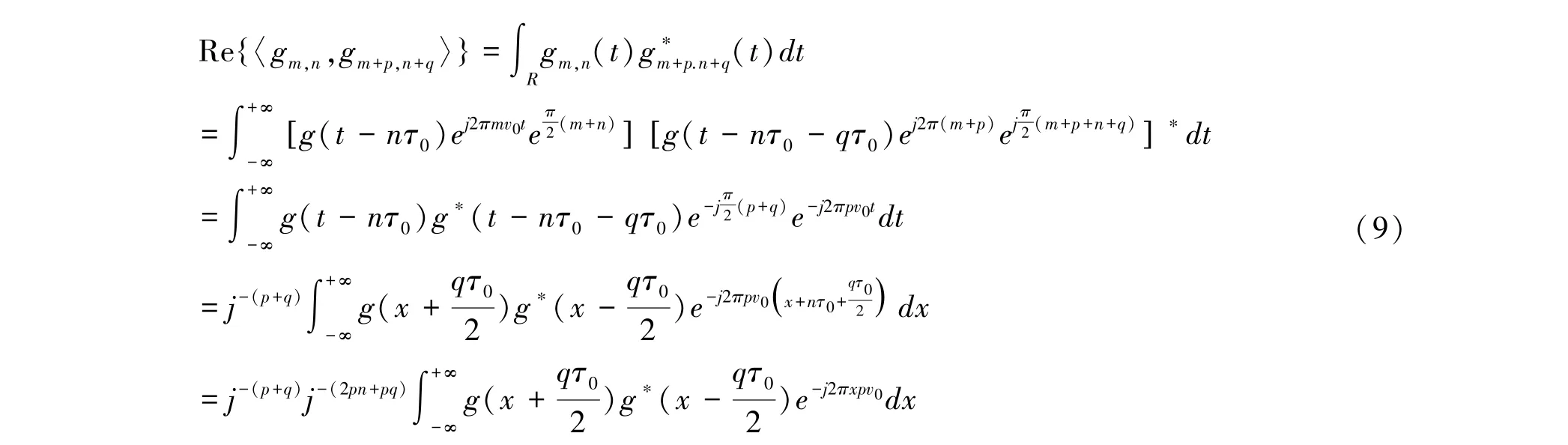
其中Ag(qτ0，pv0) 表示原型滤波器的模糊函数且

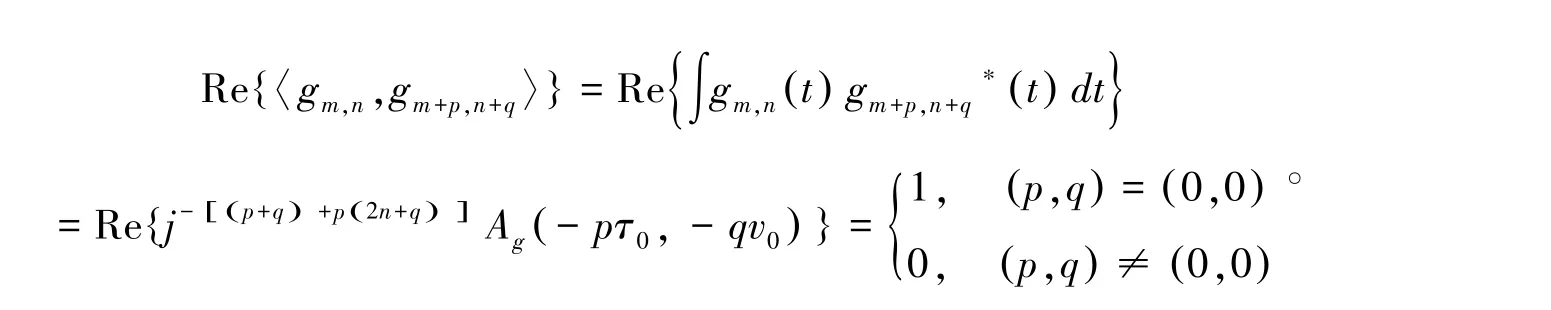
因此，我们可以得到

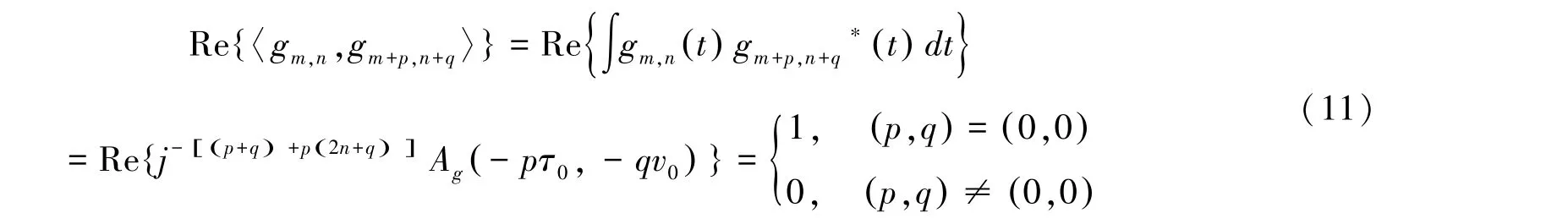
综上分析，OFDM/OQAM 依靠滤波器基函数之间实部的正交性便可以实现子载波之间的正交性，即使没有CP 也可以实现信号的正确解调。

2.2 滤波器设计

OFDM/OQAM 波形与传统添CP-OFDM 相比，可以利用特殊设计的原型滤波器取代CP 和CS 抵抗ISI 和ICI，从而保证信号传输的鲁棒性。另外，OFDM/OQAM 为了获得更优的时频特性放宽了子载波之间的正交条件，由复数域变为实数域，正交条件的保证也依赖特殊设计的滤波器。 因此，我们可以看出滤波器在OFDM/OQAM 系统中发挥着基础性作用，实际上，长久以来滤波器的设计和选用也是OFDM/OQAM 系统的关键技术研究，对系统性能有着重要影响。

2.2.1 高斯函数滤波器

高斯函数滤波器是OFDM/OQAM 系统中一类比较基础的滤波器，高斯函数可以定义为:根据文献[19]所述，高斯函数的傅里叶变换仍旧是高斯函数。 因此，高斯函数滤波器的能量在时间和频率上具有对称性。 将文献[19]中的高斯函数带入公式(10)，可以得到:

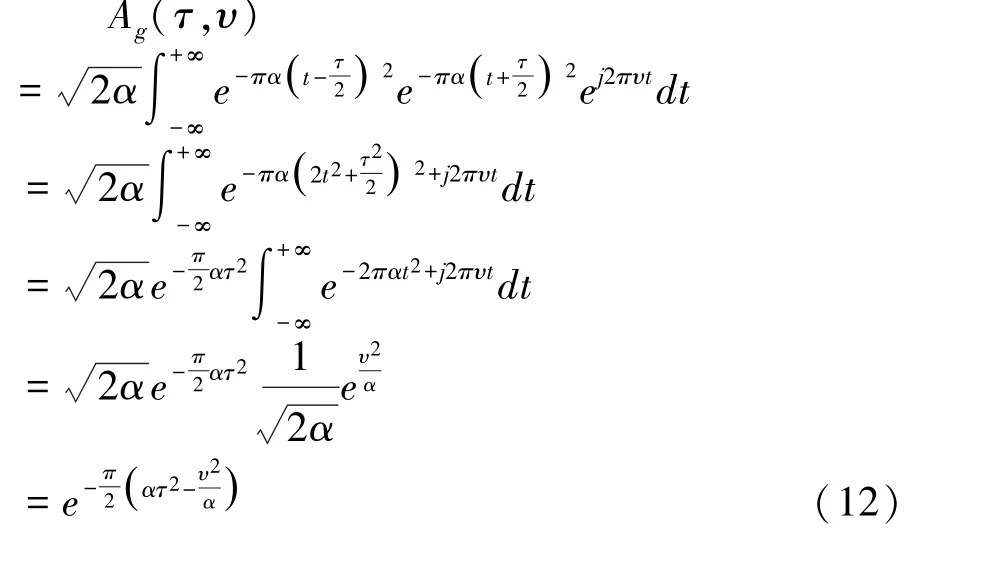
根据公式(12)可以看出，高斯函数滤波器的模糊函数有随着时间τ 频率υ 增加而呈指数递减的现象，这有助于能量集中在视频格点附近，防止能量泄漏，进而提高系统的抗击ISI 和ICI 的能力。 其等高线示意图如图所示:

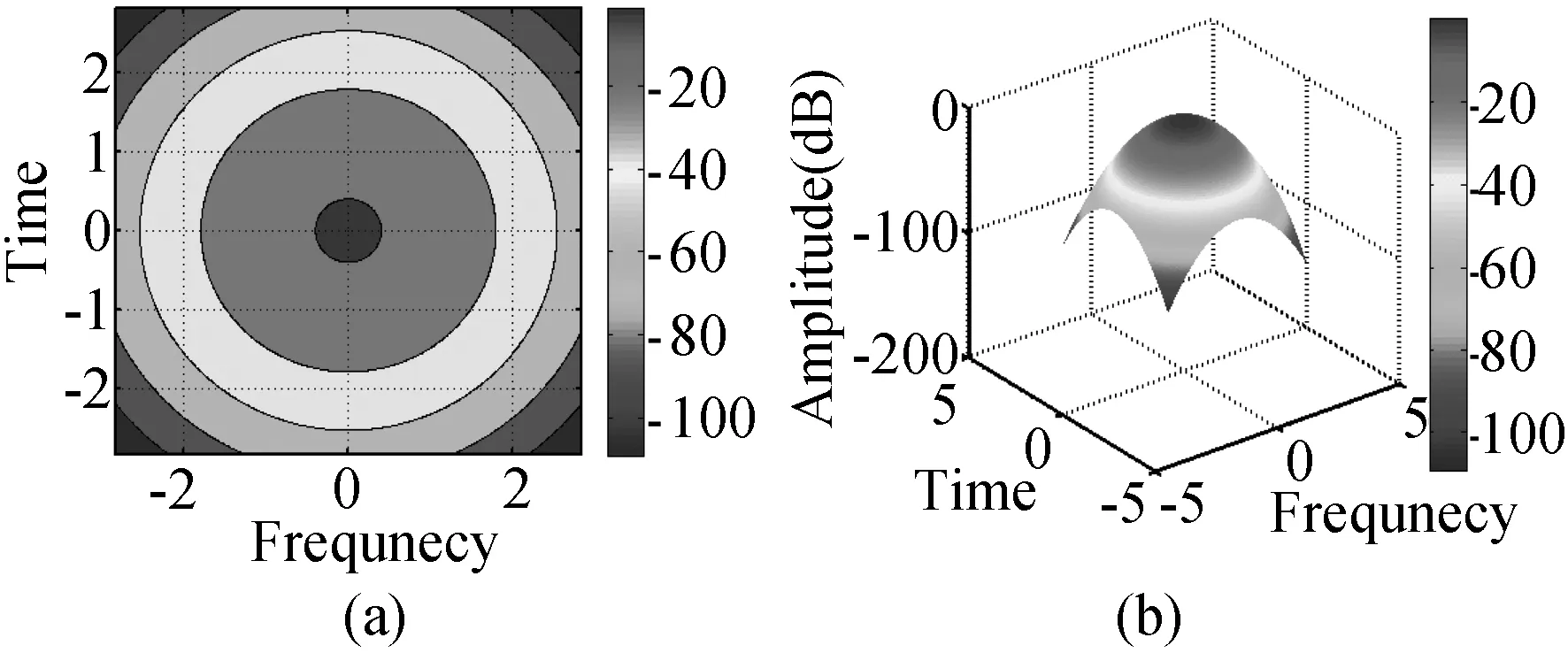
图3 高斯滤波器(a)等高线图，(b)3D 能量图

根据图3，我们可以直观的看到高斯滤波器的TFL 特性。 但是，高斯函数gα(t) 总是正的，这就导致我们无法得到正交基，其应用场景必然是非正交的，为系统接收端信号的正确解调带增添了复杂度。 因此，为了解决这个问题，人们引入了扩展高斯函数(EGF)滤波器。

2.2.2 扩展高斯函数(EGF)滤波器

扩展高斯函数 (EGF: Extend Gaussian Function)是在高斯函数的基础之上的通过演变得到的新函数，其目的在于保持高斯函数滤波器优良TFL 特性的同时解决其功能的限制——无法得到正交基。 EGF 滤波器控制其系数α 可以得到不同波形，当α〉1 时，EGF 函数能量在频率上更加集中，在时间上更加发散，当α ＜1 时，EGF 在时间上更加集中，在频率上更加发散，当α＝1 时，EGF 函数在图像上具备各项同性性质，我们称之为各向同性正交变换函数(IOTA: isotropic orthogonal transform algorithm)。 根据文献[21]，其定义式为:

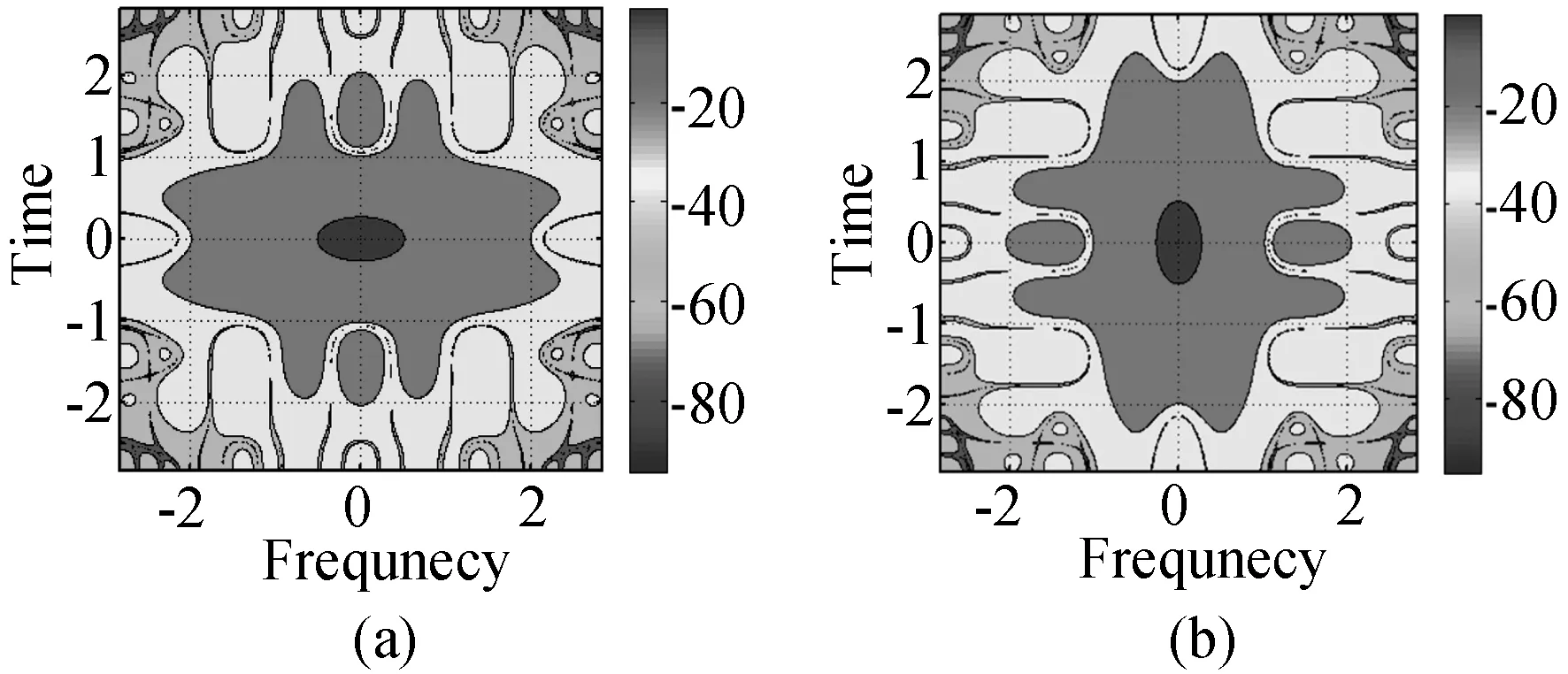
图4 EGF 滤波器二维模糊函数等高线示意图：

图5 IOTA 滤波器模糊函数(a)等高线图，(b)3D 图

2.2.3 IOTA 滤波器

本小节和我们分析了Nyquist 滤波器以及OFDM/OQAM 系统中常用滤波器的TFL 特性，常用的滤波器有高斯滤波器，EGF 滤波器以及IOTA 滤波器。 对于高斯滤波器，其傅里叶变换仍然是高斯函数，能量在时频方向上具有很好的对称性。 EGF 滤波器弥补了其不能构造正交基的缺点，尤其是变换方向参数构造的IOTA 滤波器，不仅满足奈奎斯特准则，同时具备时频方向上的各向同性特点，在实际工程中得到了广泛的应用。

2.3 基于相位偏移的前导设计

由于OFDM/OQAM 正交条件从复数域放松到实数域，因此在信号经过多径衰弱信道时会受到固有虚部串扰的影响，这就高度依赖有效的信道估计和心道均衡方法。 OFDM/OQAM 系统的信道估计方法分为盲信道估计和基于前置导频序列的信道估计两大类，盲信道估计不需要在发送数据中添加导频序列，大大提高了数据的传输效率，但是在接收端需要对大量数据进行暂存，并且需要对矩阵求逆，计算复杂度非常高，因此在实际系统中不常用。 基于前置导频序列的信道估计方法分为传统的IAM 模型，PHO 模型以及TRL 模型，这三种导频模型的设计复杂度由低到高，信号传输的误码率由高到低。

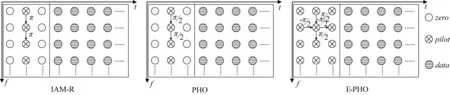
图6 三种前置导频示意图

2.3.1 IAM 模型

公式(8)描述了高斯信道下的解调出的信号以及所包含的串扰模型，因此信道估计方程可以写作:

2.3.2 PHO 模型

IAM-R 方法设计简单，只添加实数序列，但是伪导频功率较低，抗击噪声能力差。 文献[22]设计了一种相位偏移(PHO)模型(如图6(b))，这种模型特别设计中间列导频使其获得最优的伪导频功率。 借助三角函数，一阶邻域内的伪导频可以展开为:

2.3.3 E-PHO 模型

为了获得更大的伪导频功率，本文在PHO基础上设计一种扩展PHO 模型，保留中间列导频的相位偏移同时把两侧导频进行有效填充，从而获得更大的伪导频功率，本文把这种模型成为E-PHO 模型，时频格点图如图6(c)。 我们以中间列导频为基础对其一阶邻域的干扰造成的衰弱进行建模:

3 仿真结果和分析

本文利用商用软件VPItransmissionmaker9.9来验证色散信道下所介绍算法的有效性。 在这一部分中，我们考虑了IOTA 滤波器、Gaussian 滤波器和EGF 滤波器来构造滤波器组，以便进行比较。 IFFT/FFT 的长度被设置成N ＝256，调制方式，我们选择4-QAM。 对于每一帧，为了便于信道估计，在前导中插入三个OFDM/OQAM 块作为导频序列。 对于每一个OFDM/OQAM 块，我们等间隔插入8 个子载波导频来更好地纠正相位。 每帧都包含100 个OFDM/OQAM 块。 原型滤波器的脉冲长度为K ＝4N ＝1024，保证了公式(4)中假设的有效性。 为保证通用性，采样速率设为10 GS/s。 考虑到所有的导频冗余、前置量和7%的前向纠错开销，10 GS/s 采样率的光OFDM/OQAM 的净比特率和原始比特率分别为15.32 Gb/s 和16.39 Gb/s。 所占用的带宽是8.83 GHz。 因此，净光谱效率和原始光谱效率分别为1.74 bit/s/Hz 和1.86 bit/s/Hz。 假设DAC和ADC 都具有无限带宽且没有量化噪声。 光纤链路由几个跨度为100 km 的SSMF 组成，每个跨度的平均损耗为20db。 光纤色散为17 ps/km/nm。

图7 E-PHO，PHO 和IAM-R 模型在600km 和2000km SSMF 传输后OSNR-BER 性能比较

图7 对比了E-PHO 方法、PHO 方法和IAMR 方法在线性传输场景下的BER 性能。 为此，设计了一种理想的无噪声掺铒光纤放大器(EDFA)，充分补偿了光纤在各个量程中的衰减。 光信噪比(OSNR)是通过在接收端输入适当的ASE 来控制的。 误码率(BER)的评估是一个随机序列的106 位与40 个随机集的ASE 噪声。为了简化讨论，假设激光相位噪声和非线性干扰是理想的。 该仿真采用IOTA 滤波器作为原型滤波器。 如图7 所示，在600 km 和2000km 直线传输时，E-PHO 方法的BER 性能明显优于PHO方法和IAM-R 方法，这主要是由于公式(19)中给出的E-PHO 模型获得了伪导频功率的提升。如图7 所示，PHO 方法比IAM-R 方法具有更好的误码率性能。 这主要是由于虚导频的引入加强了伪导频功率。 在低到中等的OSNR，例如1到3dB， E-PHO 方法的优势不是很明显。 这可以解释为，在这种情况下，与ASE 噪声相比，伪导频功率相对较低。 E-PHO 方法的优点在中到高OSNR 时更明显，例如大于4dB。 在图7 中，E-PHO 和PHO 方法在BER 目标处所需的OSNR 分别为3.2dB 和3.7dB。 利用E-PHO 法获得了0.5dB 的OSNR 优势。

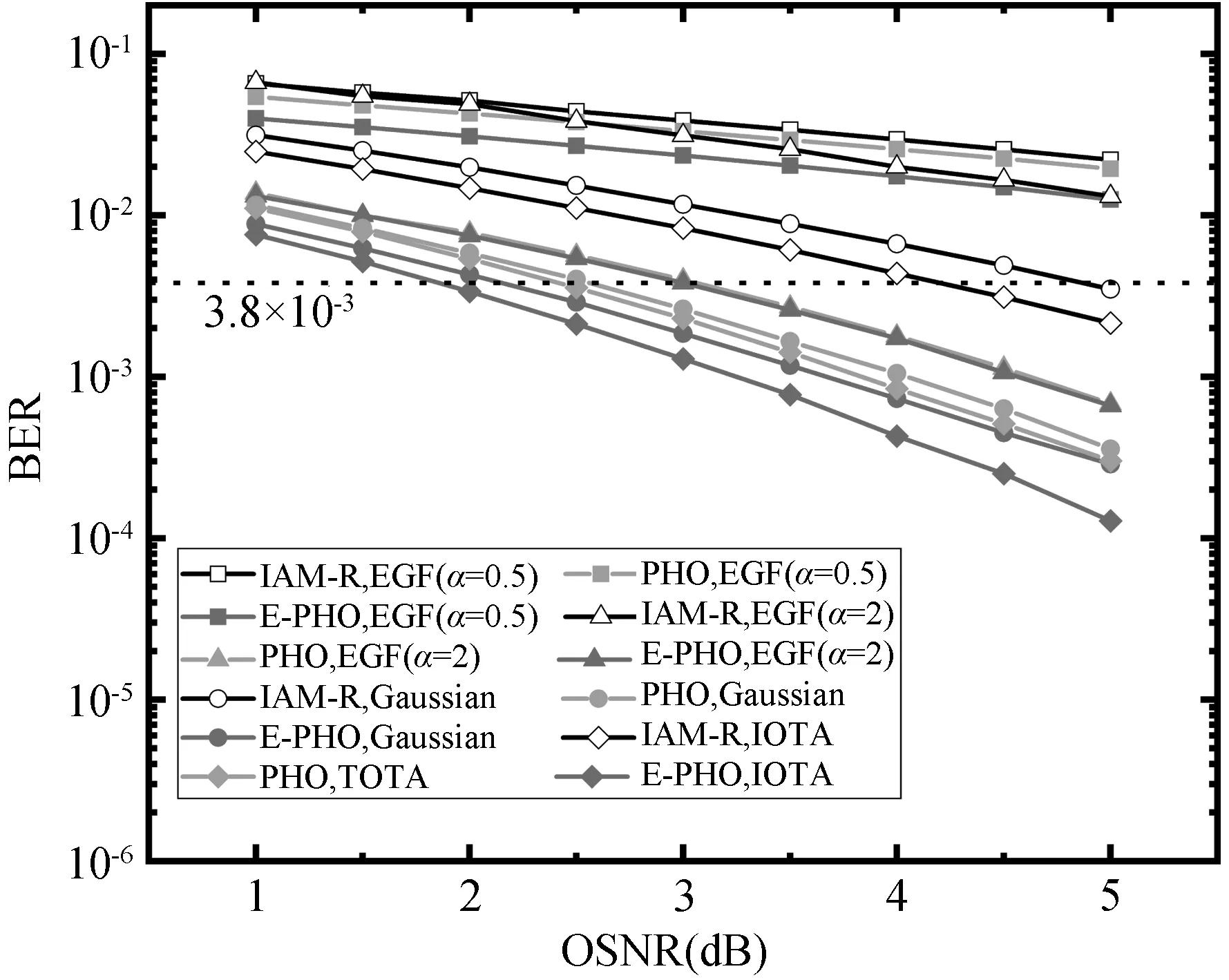
图8 E-PHO，PHO 和IAM-R 模型在600kmSSMF传输后，不同滤波器下OSNR-BER 性能比较

图8 对比了E-PHO 方法、PHO 方法和IAMR 方法在使用不同原型滤波器的线性传输场景下的误码率性能。 该部分假设了相位噪声是理想的并且没有非线性损伤。 如图8 所示，选用TFL 特性优良的滤波器可以提高OFDM/OQAM系统信号传输的有效性，EGF 滤波器在α ＝2 或α ＝05 时存在时间或频率上的能量泄漏，因此误码率性能最差，IOTA 滤波器TFL 特性良好，并且容易构造正交基底，因此误码率性能最优。 如图8 所示，在使用IOTA 滤波器、EGF 滤波器和高斯滤波器时，E-PHO 比PHO 和IAM-R 的性能有所提高。 这主要是由于2.3 节理论中E-PHO模型有着较有的噪声抑制性能。

5 结论

与传统的OFDM 波形相比，OFDM/OQAM由于去除了CP 和CS，因此更容易受到ISI、ICI以及各种干扰噪声的影响。 OFDM/OQAM 系统传输信号的准确解调有赖于良好TFL 滤波器的选用和有效的信道估计。 本文在相干光通信系统中详细地推导了OFDM/OQAM 系统传输模型，并验证了其正交性。 对于滤波器算法设计，本文通过理论建模以及等高线能量分布图分析了Gaussian 滤波器、EGF 滤波器以及IOTA 滤波器的TFL 特性；对于信道估计算法设计，本文分析了常用的IAM-R 模型、PHO 模型，并提出了一种基于导频序列有效填充的E-PHO 模型。 通过理论分析和仿真验证，TFL 特性良好的滤波器可以提高系统的误码率性能；E-PHO 模型通过扩展导频序列提高了伪导频功率，改善了系统传输的有效性。