量子回归算法综述∗

高 飞 潘世杰 刘海玲 秦素娟 温巧燕

北京邮电大学，北京市 100876

引言

随着信息技术的高速发展，全球数据总量每年指数增长，这使得经典机器学习算法在处理大数据时将面临计算性能的巨大挑战。 量子力学独特的性质使得量子计算在处理某些特定问题上相比于经典计算具有显著的速度优势。 近年来各研究机构和IT 公司聚焦于研究用量子算法解决经典机器学习问题，进而出现了一个新型交叉领域—量子机器学习[1]。 该领域的一些成功实例包括量子主成分分析[2]，量子分类算法[3，4]，量子数据聚类[5，6]，量子神经网络等[7]。

2012 年，Wiebe 等首次提出一个基于HHL算法[8]的量子线性回归算法[9]。 当数据矩阵是稀疏矩阵且具有很低的条件数时，该算法相对经典算法具有指数加速效果。 后来，Liu 和Zhang对该算法进行了简化，提出复杂度更低的量子线性回归算法[10]。 2016 年，Schuld 设计了用线性回归预测新数据的量子算法[11]。 当数据矩阵低秩时，该算法相对经典算法具有指数加速效果。2017 年，Wang 提出一个输出经典形式拟合参数的量子线性回归算法[12]，相比经典算法，该算法的复杂度在样本数目因子上具有指数加速效果。同年，Yu 等提出一个量子岭回归算法[13]，该算法在数据矩阵为低秩时具有指数加速效果。 此外，他们也提出一个评估岭回归预测性能的量子交叉验证算法。 2019 年，Li 等基于稠密矩阵线性系统求解算法[14]提出非稀疏矩阵的量子岭回归算法[15]，该算法相对经典算法在数据矩阵的维度上有多项式加速效果。

本文将综述量子回归算法近年来的重要进展，并借鉴文献[16]的思想给出一个基于梯度下降法的量子逻辑回归算法。 文章安排如下:第一节介绍一些基础量子算法，它们已被广泛应用于量子机器学习；第二节对经典回归算法进行简单的回顾；第三节介绍典型的量子回归算法；第四节对文章做了总结。

1 量子基础算法

1.1 哈密顿量模拟

1982 年Feynman 指出用经典计算机模拟量子系统的复杂度会随着qubits 数目呈指数级增长，并提出量子计算机模拟量子系统的构想[17]。封闭量子系统的演化遵循薛定谔方程:

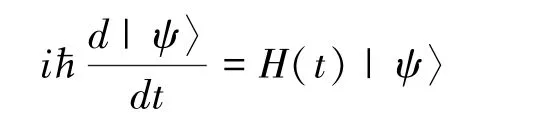
其中ћ被称为普朗克常数，H为系统的哈密顿量。 当H与时间无关时，有｜ψ (t)〉＝e-iHt ｜ψ(0)〉。 即给定初态｜ ψ(0)〉， 在一个不随时间变化的量子系统中演化t时间，那最终会得到量子态｜ψ(t)〉。 哈密顿量模拟是指给定访问Hermitian 矩阵H的量子黑盒(quantum oracle)、任意时间t以及误差∈， 设计一个量子电路U使其以精度∈近似酉操作e-iHt，即

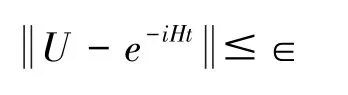
针对不同的矩阵输入模型，有不同的哈密顿量模拟的方式，复杂度也各不相同。

表1 典型哈密顿模拟方法

1.2 量子相位估计

相位估计算法[14，21]是一个重要的量子算法，已经作为子算法被成功嵌入到多个量子算法中[8，9，22]。 它的目标是把酉算子的相位信息(或量子模拟中哈密顿量的特征值信息)存储到计数量子寄存器中。

量子相位估计[14]:令酉算子U:U ｜ vj〉＝exp(iθj)｜vj〉，其中θj∈[-π，π]，j∈[n]。 那么存在一个量子算法可将量子态∑j∈[n]αj ｜vj〉变换为∑j∈[n]αj ｜vj〉｜〉，使得对所有的j∈[n]，满足算法的成功概率为1-1/poly(n) ，复杂度为O(TUlog(n)/δ) ，其中TU为实现U的复杂度。

1.3 Grover 搜索

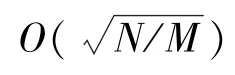
在经典搜索算法的搜索过程中，需要一个可以判断随机采样的第x个元素是否为目标元素的函数f(x)，不失一般性，假设

在量子情形下，类似于经典算法，需要利用f(x)来构造一个量子黑盒O来“判断” 第x个元素是否为目标元素:O ｜ x〉｜ q〉＝｜ x〉｜ q⊕f(x)〉。 利用黑盒O来构造G算子:

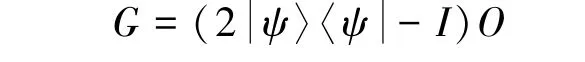
在该算法中，｜ψ〉 为n个量子比特的均匀叠加态，即

1.4 幅度估计

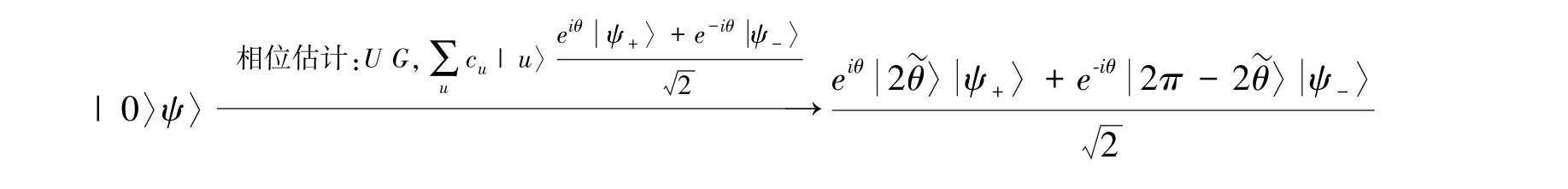
1.5 受控旋转

受控旋转解决的问题是如何有效地把信息从计数量子寄存器中提取到量子态的振幅上。

受控旋转[25]:令θ∈R，θ˜是θ的d比特有限精度表示，则存在酉矩阵Uθ，满足:

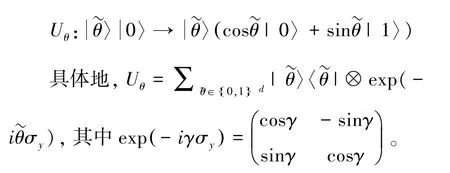
1.6 量子交换测试(Swap Test)

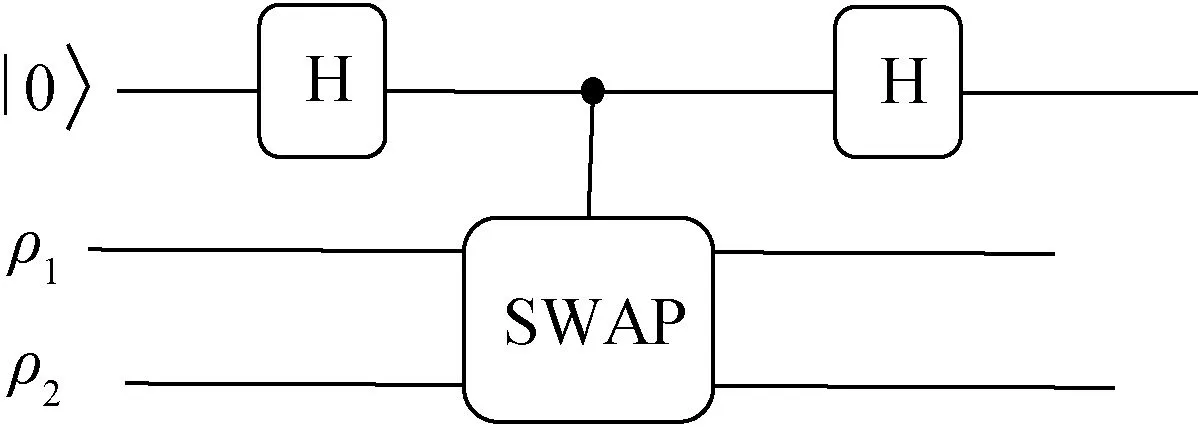
图1 交换测试的量子线路。 测量顶部的辅助量子比特获得测量结果为0 的概率为 ＝ +Tr ( ρ1ρ2) 。 重复运行该电路足够多次可得到Tr ( ρ1ρ2) 的估计值。

2 经典回归算法

2.1 一般线性回归

2.2 岭回归

当数据点自变量存在多重共线性使得XTX不可逆或者遭遇过拟合时，一般线性回归的拟合效果往往不能令人满意[27，28，29]。 为了克服这两个问题，Hoerl 等提出岭回归模型[28]。 岭回归是一般线性回归的扩展，和一般线性回归不同的是，岭回归是在一般线性回归引入w的正则化项，使其最终的最优拟合参数为

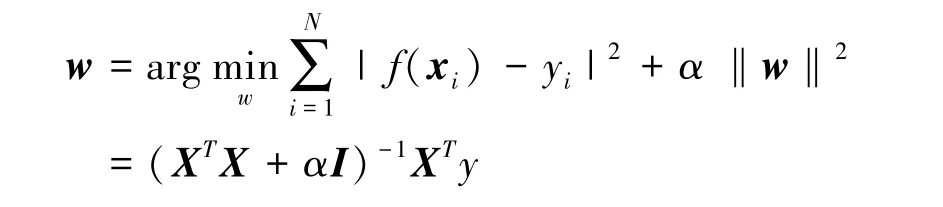
其中α记为岭回归参数，I为单位矩阵，且‖w‖为任意向量w的2-范数。 很显然，一般线性回归是岭回归在α＝0 下的特例。

找出一个好的正则化参数α 使得岭回归在该参数下具有较好的预测性能，并算出相应的最优拟合参数w在实际应用中具有重要意义。

2.3 逻辑回归

逻辑回归是机器学习与模式识别中最重要的分类算法之一，被广泛应用于医疗、人脸识别、金融等领域[30]。 二元逻辑回归是最简单的逻辑回归模型，其回归函数为非线性函数

其中xi和yi分别是第i个训练样本以及其对应的类别。

因为上式中函数的最小值没有闭式解，所以需要结合一些优化手段(如梯度下降、牛顿法等)以迭代方式进行求解。 一般采用梯度下降法来求解参数w， 该优化算法的核心任务是计算出每次迭代中的梯度:

3 量子回归算法

本节将介绍具有代表性的量子回归算法。具体来说， 3.1 节分别介绍了模型参数w的输出为量子态以及输出为经典形式的量子线性回归算法，3.2 节介绍量子岭回归算法，3.3 节借鉴文献[16]的思想给出一个基于梯度下降法的量子逻辑回归算法。

3.1 量子线性回归算法

3.1.1 输出量子态｜w〉 的量子线性回归算法

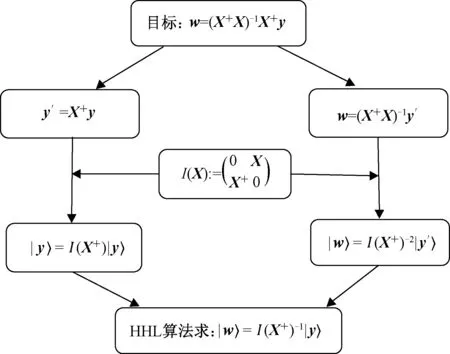
图2 Liu 等的一般线性回归的量子算法

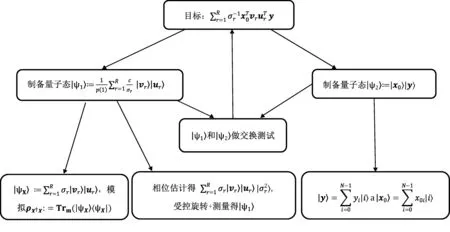
图3 Schuld 等算法的大致流程

3.1.2 获得参数w经典信息的量子线性回归算法

另外，Wang还设计了一个量子算法来估计拟合的质量，可用于提前检查给定的数据集是否符合线性回归模型。 拟合质量的定义与WBL[9]方法相同，但该算法采用相位估计算法的一个变体[35]来标记想要的特征相位，接着运用类似HHL算法的方法得到拟合质量。 这里不做详细介绍，具体内容见文献[12]的定理3。

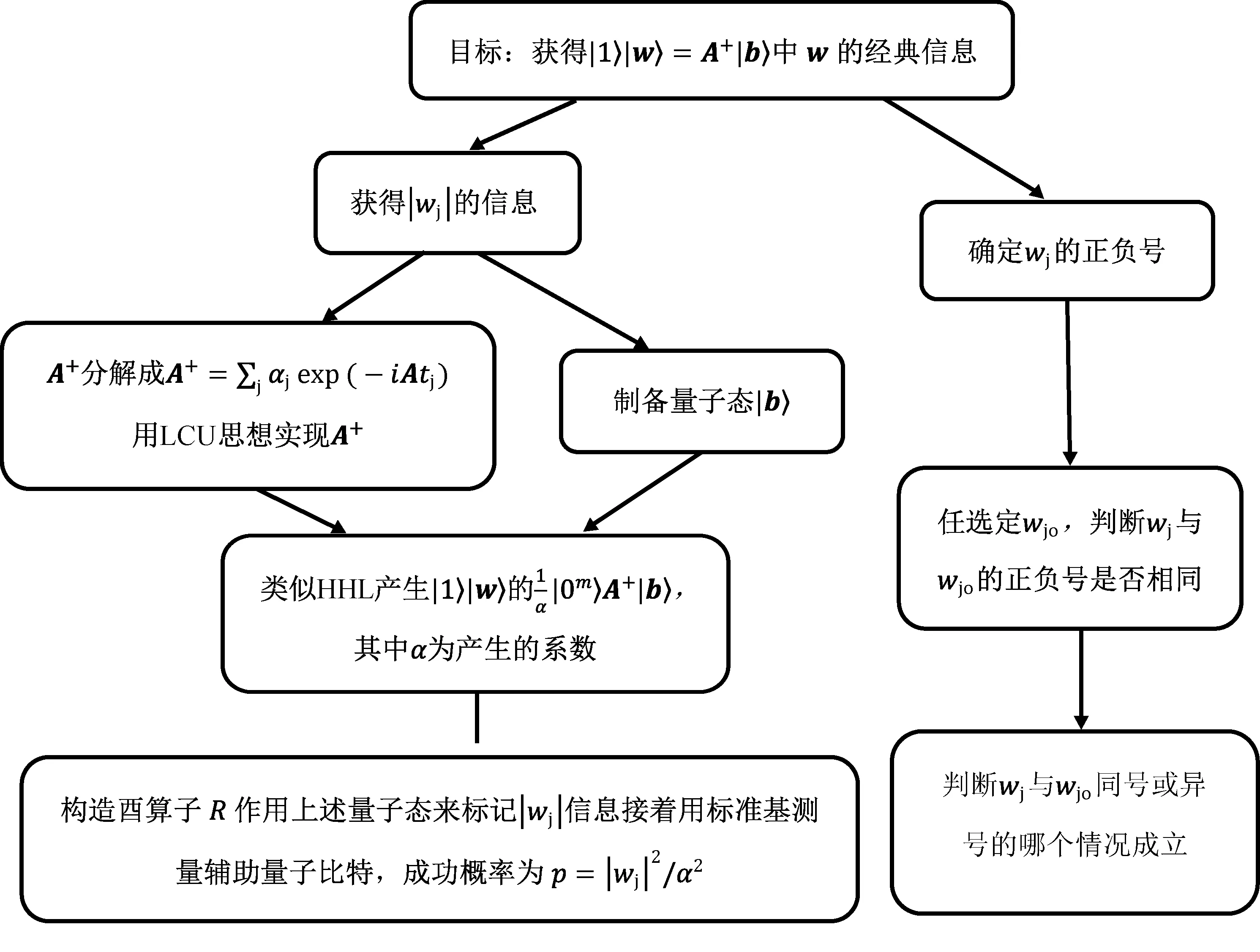
图4 获得最优参数w 的经典信息的量子算法

3.2 量子岭回归算法

2017 年，Yu等提出一个数据矩阵为低秩矩阵的量子岭回归算法[13]。 另外，为了高效评估岭回归预测能力，他们还设计了量子K重交叉验证算法来选取一个好的正则化参数α。

首先介绍量子岭回归算法(子算法1)，该算法输出为一个量子态，其幅度以误差∈近似w的归一化形式。 该算法类似于量子线性回归算法，需将X扩展到一个厄米矩阵

另外，Yu等把上述量子岭回归算法作为子算法，设计了量子算法做岭回归的K重交叉验证，以便选取一个好的岭回归参数α使得量子岭回归具有很好的预测性能。

经典情形下，可采用下面的K重交叉验证法来确定一个好的α:

(1)将N个初始数据点的集合分为K(2 ≤K≤N)个子集，且第l(l＝1，…，K)个子集包含数据点{(xj，yj)｜ j∈Sl}， 其中Sl:＝{(l-1)N/K+ 1，…，lN/K} 用于标记分配到第l子集中数据点的编号；

(2)执行K轮训练-测试过程。 对于第l轮，第l子集被选为测试集合，而其他子集作为训练集；

(3)计算所有数据的残差平方和E(α) 作为评估具有该特定候选α参数下岭回归的预测，性能的指标；

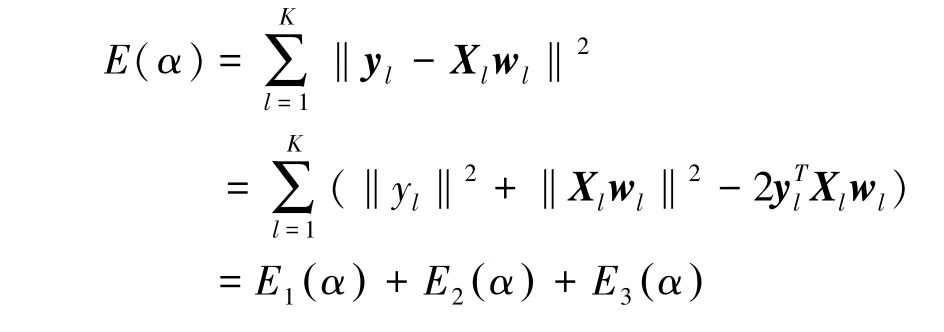
(4)最后，选择一个具有最佳预测性能的候选α 作为最终的岭回归参数α。

计算E(α) 的量子算法过程简述如下:令Xl∈R N/K×M为X中包含Sl指定的行，即对应了第l个子集，X-l∈R N×M为X但Sl所指定的行的元素均用0 代替。 在初态上引入一个附加寄存器存储Sl的信息，作为控制位控制做量子模拟的时候选取的矩阵X-l。 用类似于子算法1 的过程制备量子态

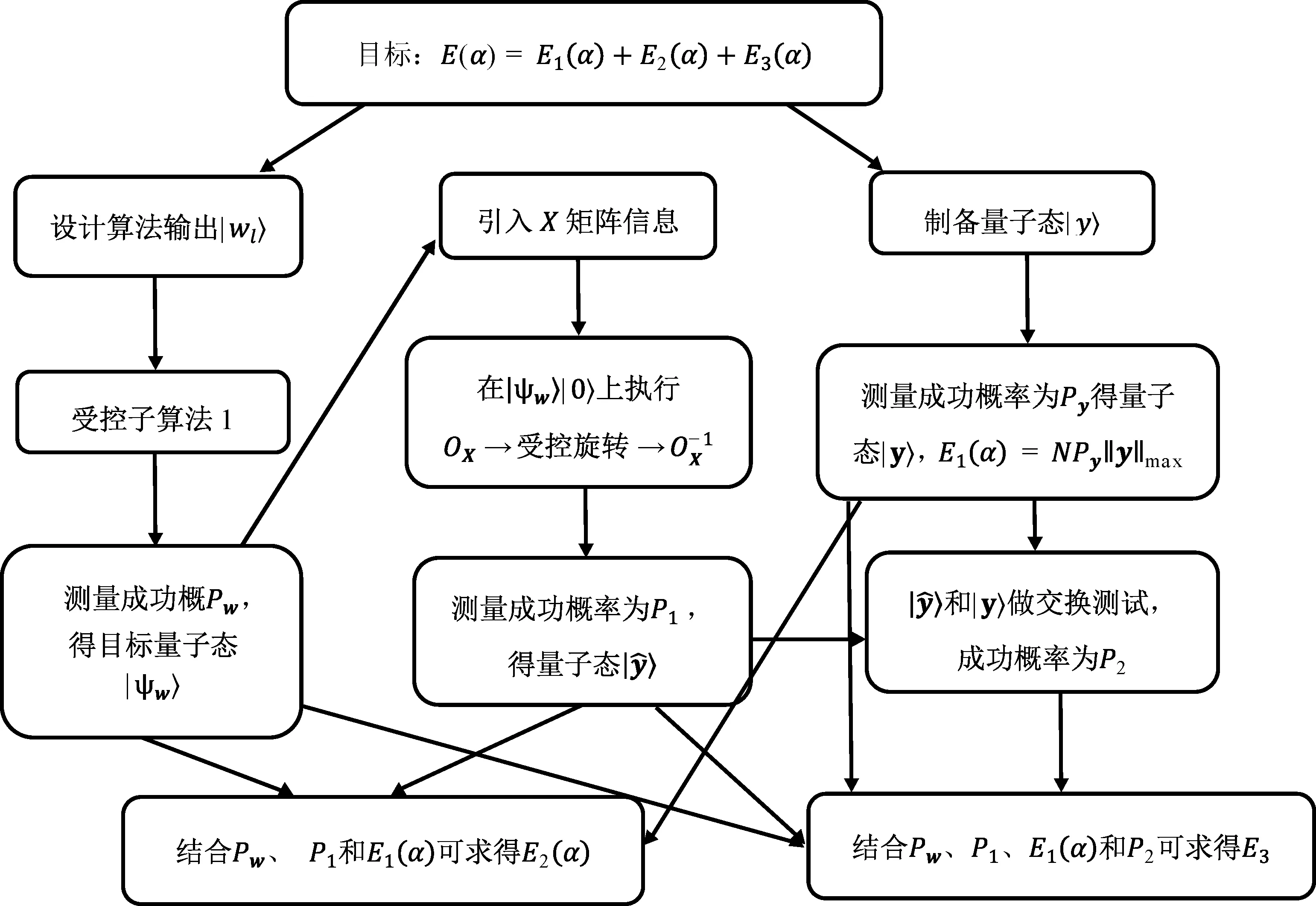
图5 量子K 重交叉验证算法

3.3 量子逻辑回归算法

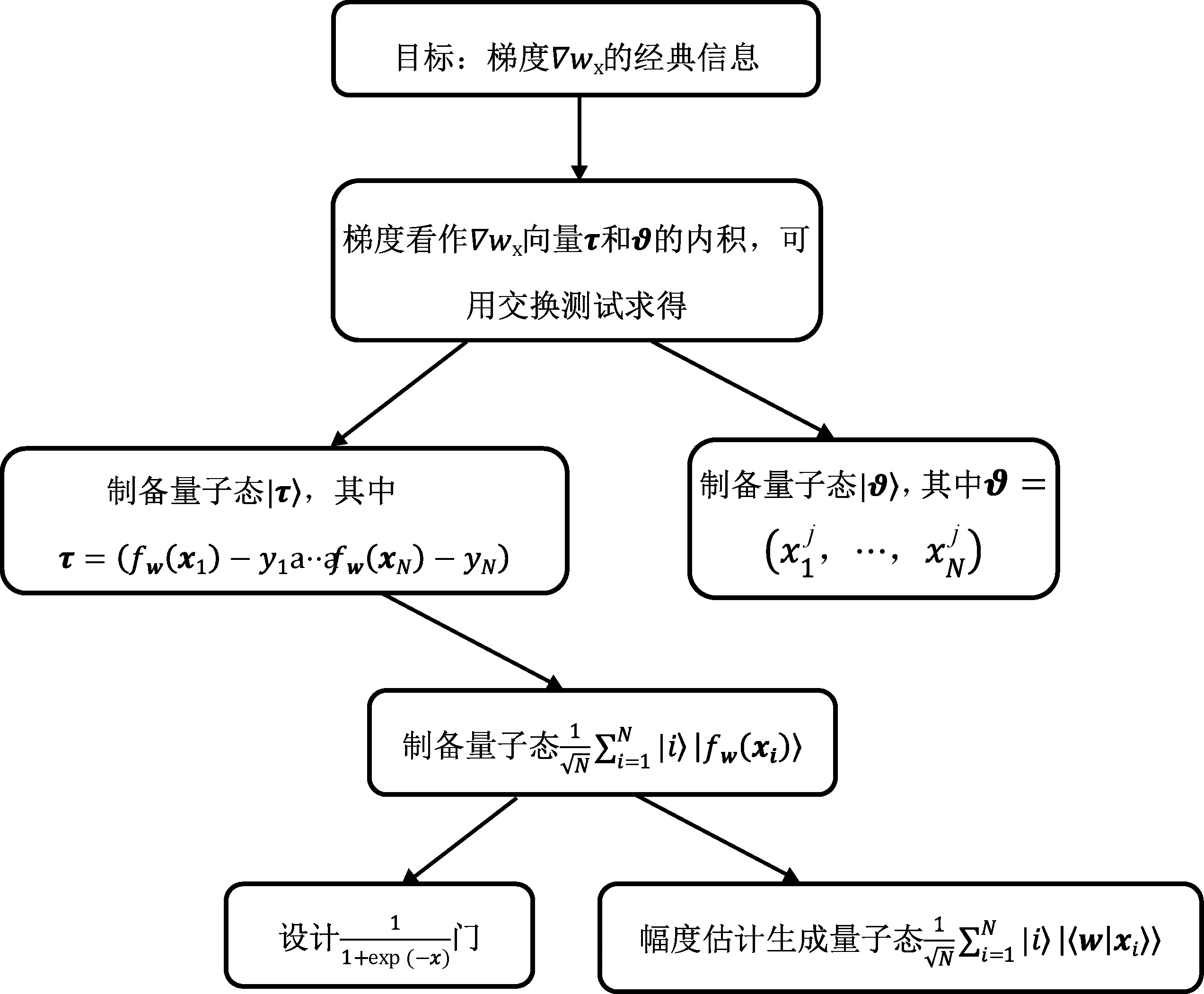
图6 获得梯度∇wj 的量子算法

4 结论和展望

量子计算在解决某些机器学习问题时展现出强大的计算能力。 本文综述了量子回归算法近年来的重要进展，包括量子线性回归、量子岭回归算法，并提出一个基于梯度下降法的量子逻辑回归算法。 这些量子算法在合理的假设条件下相比经典算法有指数加速效果，展现出了量子计算的独特优势。 目前，针对Lasso 回归、Elastic Net 回归等问题还没有相关的量子快速算法，它们可能是未来的研究方向。 此外，如何在量子回归算法中增加隐私保护的功能，也有待解决。 随着大数据和量子计算的快速发展，我们期待在未来量子计算能解决更多的经典机器学习问题。