9-量子团簇态信道的非对称双向量子信息传输*
2020-02-20彭家寅
彭家寅
内江师范学院 数学与信息科学学院,四川 内江 641199
1 引言
量子纠缠作为一种量子资源被用来进行不同类型的量子信息处理,如量子隐形传态[1-4]、量子超密编码[5]、量子态分享[6-9]、远程态制备[10-12]、量子信息凝聚[13]等。由Bennett等[1]在1993年首先提出的隐形传态是将一个任意单量子未知态从一个地方传送到另一个遥远的地方,而没有该量子自身在空间中的物理传送。在这开创性工作之后,一些研究者利用不同类型的量子信道,设计出了许多隐形传态协议[3-9]。最近,Zha等[14]提出了双向受控隐形传态方案:信息传输的两方在第三方的控制下,可以同时交换他们的任意单量子未知态。此后,一些学者提出以不同量子纠缠态为信道的相互传输量子态的若干方案[15-21],其中非对称的双向受控隐形传态方案是由Zhang等[18]于2015年首先提出的,该方案以7-量子最大纠缠态为信道,在监控者的控制下,Alice可以传送她的单量子态给Bob,同时Bob也能传递他的任意二量子态给Alice。近几年来,这方面的研究得到了发展[19-21]。
2000年,Lo率先提出远程态制备的概念[10],它是已知量子态的隐形传态,即通过事先分享量子纠缠和适当测量以及经典通信,发送者能够为遥远的接收者制备一个已知量子态。到目前为止,出现了许多不同的远程态制备方案,如确定的远程态制备[22-23]、联合远程态制备[24-27]、受控的远程态制备[28-29]、双向受控远程态制备[30-31]、多跳受控远程态制备[32]、循环远程态制备[33-34]等。一些研究者分析了在受控远程态制备中监控者的控制能力问题[35],而一些远程制备方案已经实验实现[36-38]。2013年,Cao和Nguyen[31]提出了第一个受控双向远程态制备方案,在该方案中,Alice和Bob通过局部操作和经典通信,就能同时交换他们的单粒子量子态。此后,Sharma等[39]提出了概率的、确定的和联合的受控双向远程态制备三个方案。Peng等[30]于2015年雇佣8-量子纠缠态作为信道,提出五方联合受控双向远程态制备协议。2017年,另一个五方联合受控双向远程态制备方案被Wang等[40]提出,该个方案是以7-量子纠缠态为信道的。2016年,Zhang等[41]提出以6-量子非最大纠缠态为信道的联合受控双向远程态制备方案。上述方案是对称的,即利用不同量子纠缠信道,发送者能够同时给对方制备单粒子量子态。近年来,一些非对称受控双向远程态制备被提出。2017年,Sang等[42]提出了一个非对称双向远程态制备协议,一个未知单量子态被传输,同时一个已知量子态被制备。Song等[43]给出了一个对称的双向远程态制备方案,两个单粒子态同时被交换。他们还提出一个单粒子态和一个任意二粒子态被制备的非对称双向远程态制备协议。2018年,Fang等[44]提出一个双向混合量子信息传输方案,一个任意未知单粒子态被隐形传输给Bob,同时一个已知二粒子态在Alice处被制备。
本文研究9-量子团簇态在非对称双向隐形传态、非对称双向远程态制备、双向量子信息混合传输中的应用,给出三个不同类型的量子信息传输协议,指出各方案的特点,并讨论实验实现的可行性。
2 二量子态和三量子态的非对称双向隐形传态
假设Alice想要把未知三量子态式(1)传送给Bob。

其中,x和y是满足归一化条件|x|2+|y|2=1的任意复系数;同时Bob也打算将如下二量子态式(2)传递给Alice。

这里α和β是任意复系数且满足|α|2+|β|2=1。Alice和Bob事先安全地分享如下一个9-量子团簇态[21]:

其中,量子1、3、5、9属于Alice,而量子2、4、6、7、8属于Bob。

这里,量子A1、A2、A3、A4属于Alice,而Bob拥有量子B1、B2、B3、B4、B5。
由所有14个量子构成的初始复合态为:
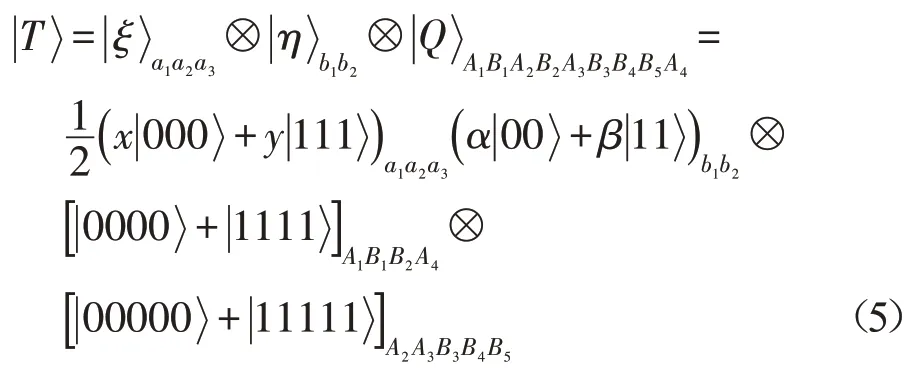
下列8个GHZ-态构成三粒子正交基:

而Bell正交基由下列向量构成:


记Pauli算子:

为完成量子任务,首先Alice需用式(6)所示的GHZ-态对粒子a1、a2和A2进行三粒子测量,然后对粒子A3施行Hadamard门H运算,这里:

再对粒子a3和A3进行Bell-态测量,并将测量结果通知Bob。具体如下:
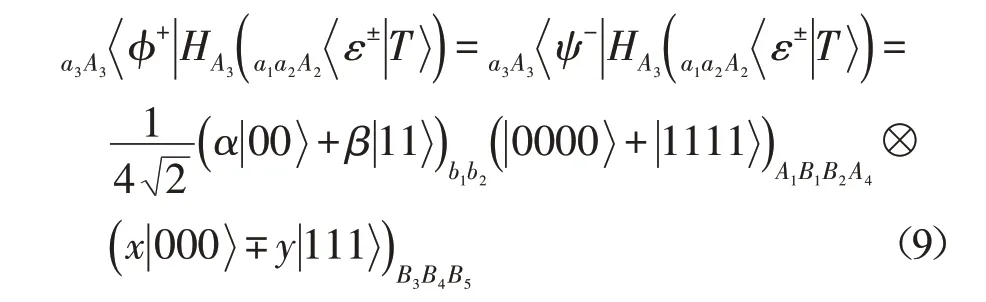
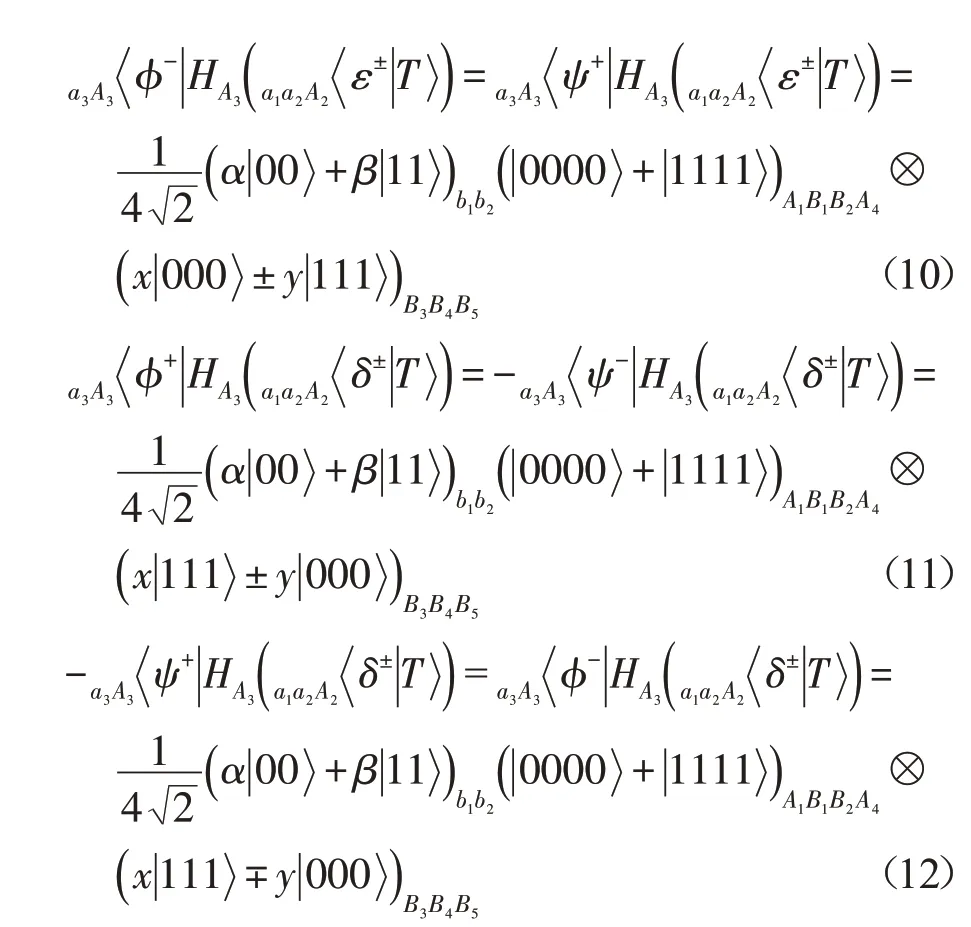
其次,Bob对粒子b1和B1进行Bell-态测量,然后对粒子B2施行Hadamard门H运算,再对粒子b2和B2进行Bell-态测量,并将测量结果告知Alice。具体如下:

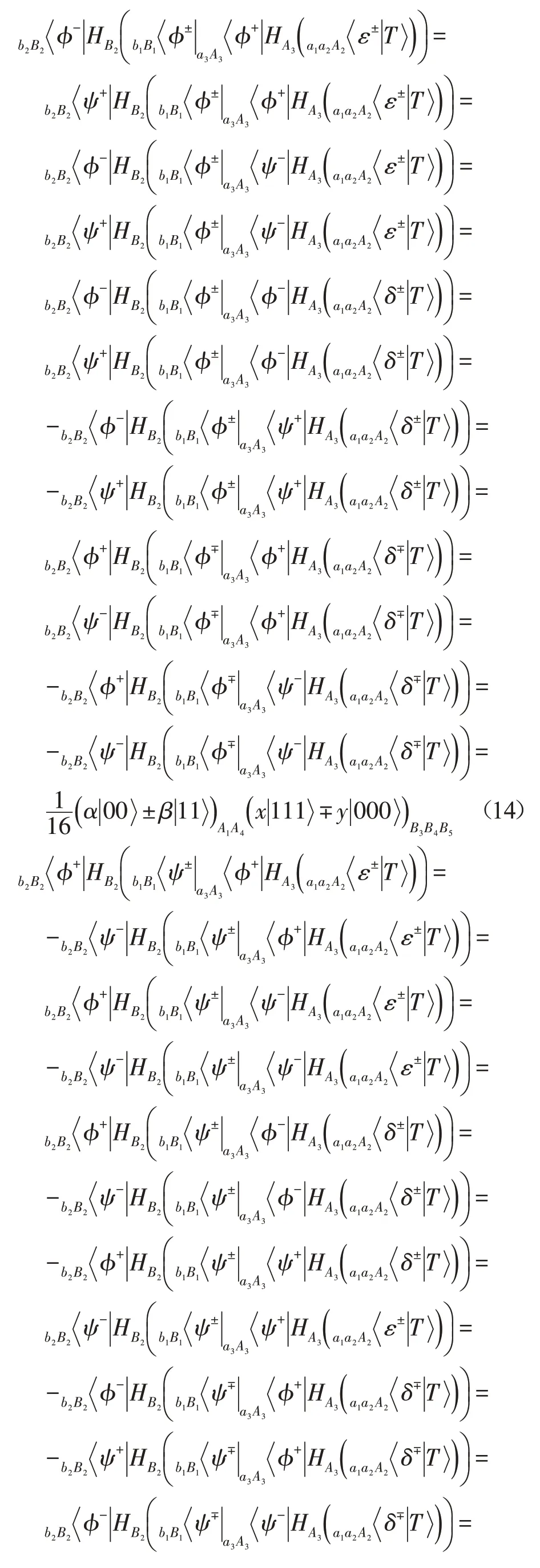

最后,由等式(13)至等式(20)可知,Alice和Bob根据收到的信息,对各自的粒子采用适当的Pauli运算就可以恢复目标态。例如:如果Alice的测量结果为,Bob的测量结果为,则剩余粒子塌陷态为:
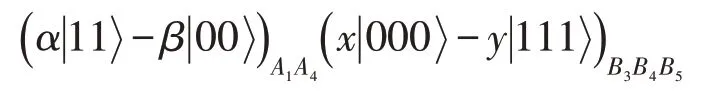
收到测量信息后,Alice对粒子对(A1,A4) 执行iσy⊗σx运算,Bob对粒子对(B3,B4,B5)施行σz⊗I⊗I运算,就可以得到:

从而Alice和Bob同时交换了他们的量子态。对于其他情形,也能得到相同的结论。这样,本文协议就成功地实现了,且因参与者交换的量子数不同,故本文方案是非对称的。
注1Alice需用式(6)所示的GHZ-态对粒子a1、a2和A2进行三粒子测量,仅出现的测量结果,这就使得方案简化了一半。
3 二量子态和三量子态的非对称双向远程制备
考虑如下情景:Alice想要在遥远的Bob处制备已知三量子态:
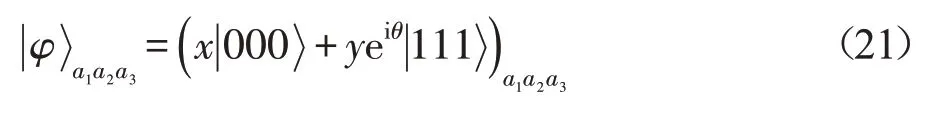
其中,x和y是满足x2+y2=1的任意实系数,θ∈[0,2π];同时Bob打算为Alice制备已知二量子态:
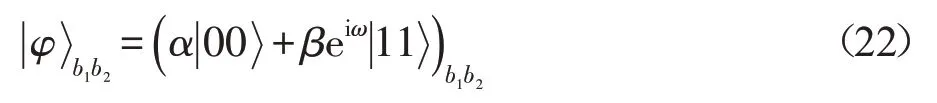
这里,α和β是任意实系数且满足α2+β2=1,ω∈[0,2π]。连接Alice和Bob的量子信道为式(4)所示的9-量子团簇态,其中量子A1、A2、A3、A4属于Alice,而Bob拥有量子B1、B2、B3、B4、B5。
为了完成此量子任务,Alice利用单粒子测量基式(23)测量粒子A2。

再采用前馈测量策略测量粒子A3,即如果Alice对粒子A2的测量结果为则对粒子A3的测量基为:

否则,对粒子A3的测量基为:

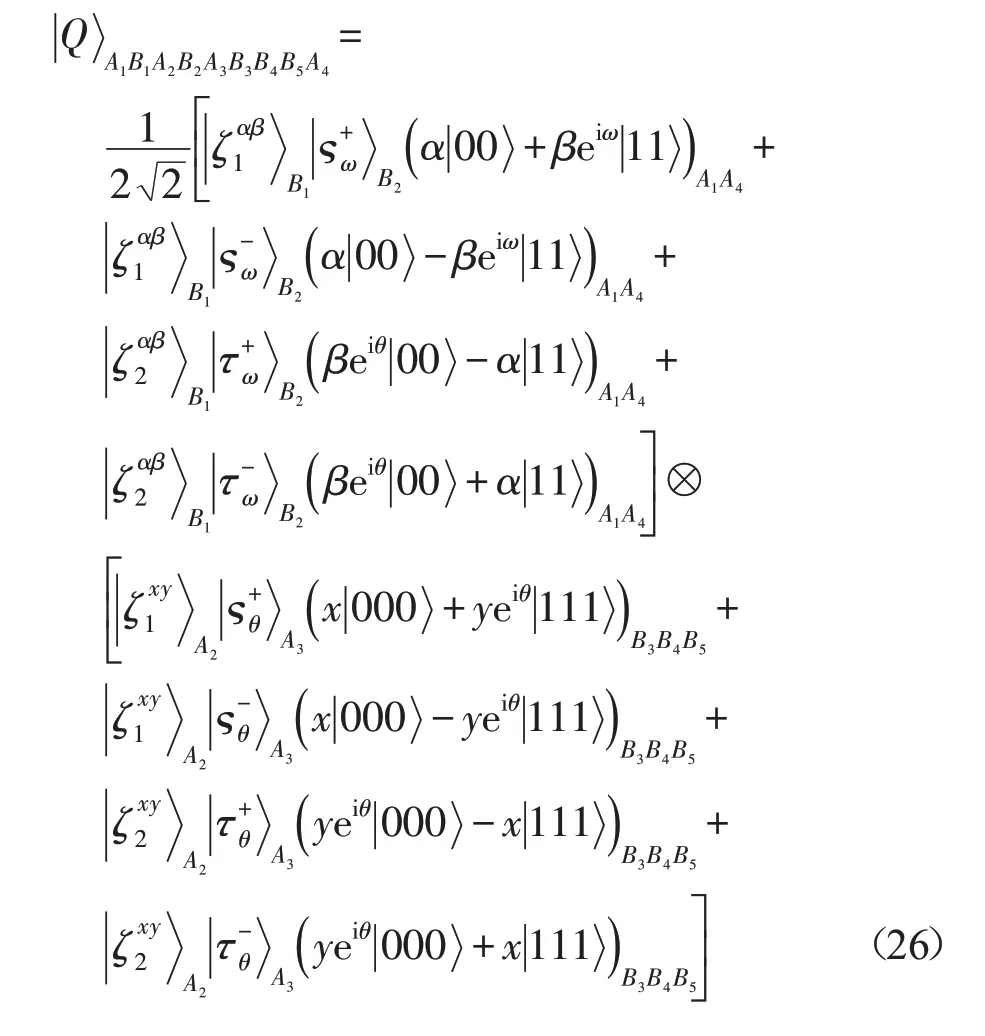
从式(26)可知,Alice和Bob根据收到的信息,应用适当的Pauli运算就可重构目标态:

也就是,Alice和Bob相互成功地制备所希望的量子态。所有测量结果及其对应的恢复运算间的关系见表1。

Table 1 Relationship between various measurement results and corresponding recovery operations表1 各种测量结果及其对应恢复运算之间的关系
注2本方案使用了前馈策略,使得方案完美实现。否则,方案成功的概率为26%。
4 二量子态制备和三量子态传输的混合非对称双向通信
假设Alice想要未知三量子态式(27)传送给遥远的Bob。
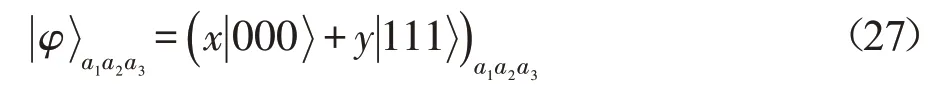
其中,x和y是满足|x|2+|y|2=1的任意复系数;同时Bob也打算在Alice处制备已知二量子态:

这里,α和β是任意实系数且满足α2+β2=1,ω∈[0,2π]。连接Alice和Bob的量子信道为式(4)所示的9-量子团簇态,其中量子A1、A2、A3、A4属于Alice,而Bob拥有量子B1、B2、B3、B4、B5。初始系统为:

为完成此量子任务,首先Alice对粒子a1、a2和A2进行GHZ-态测量,然后对粒子A3施行Hadamard门H运算,再对粒子a3和A3进行Bell-态测量,并将测量结果通知Bob。其次Bob利用基测量粒子B1,再用前馈测量策略测量粒子B2,即如果Bob对粒子B1的测量结果为,则用基测量粒子B2;否则,用测量粒子B2。最后将测量结果告诉Alice。
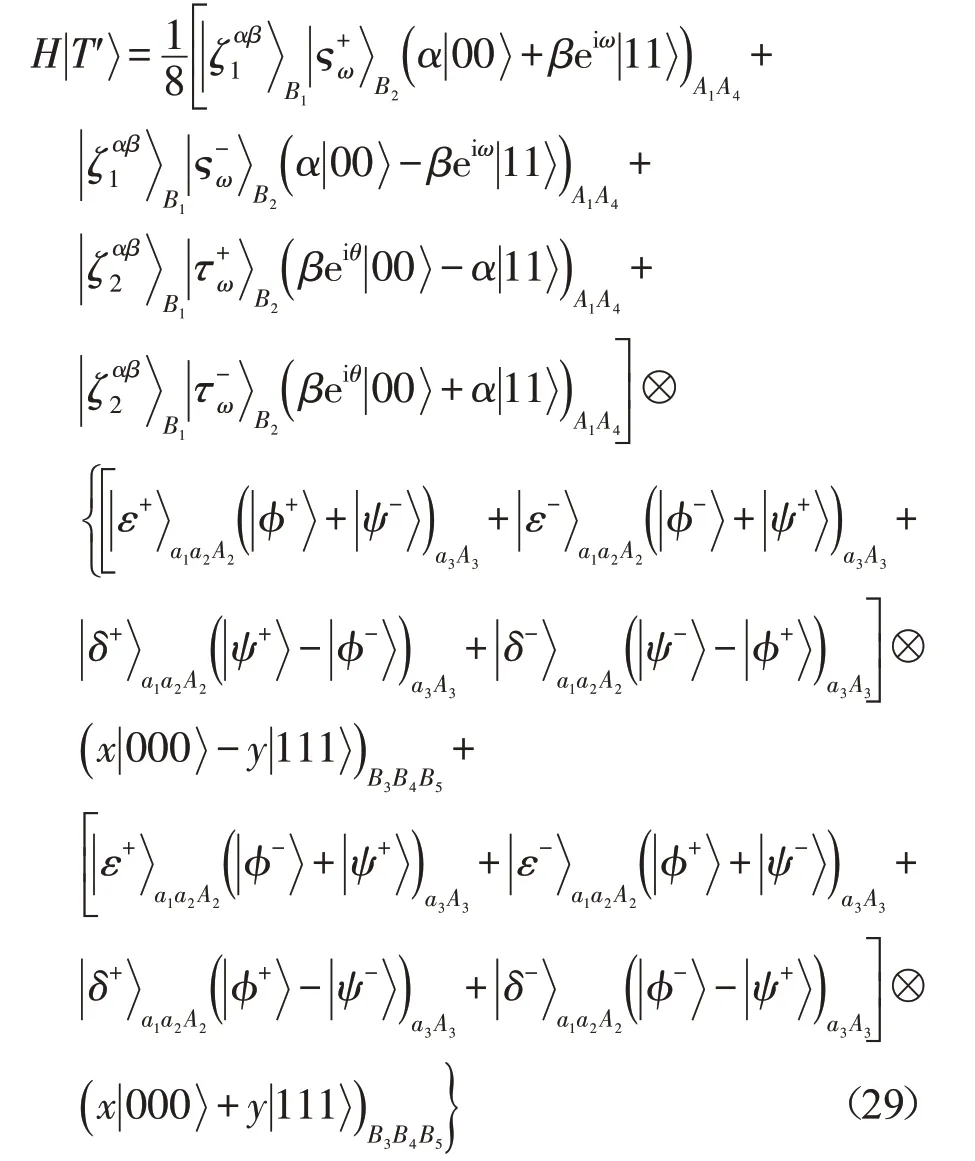
从式(29)可以看出,当Alice听到来自Bob的测量信息后,她对粒子对(A1,A4)应用I⊗I或σZ⊗I或iσy⊗σx或σx⊗σx就能获取;Bob根 据Alice的测量结果,利用变换σZ⊗I⊗I或I⊗I⊗I,就能得到。也就是,Alice和Bob的信息交换成功,混合量子通信任务成功完成。
注3本方案本质上是前两个方案的部分结合,因此它具有前两个方案的优点。类似地,容易获得二量子态传输和三量子态制备的混合协议。
5 结论
本文中三个不同类型的协议的主要资源是同一纠缠信道,其制备是量子通信理论的一个重要方面。有几种产生纠缠的实验方法,其中一些方法在文献[45-47]中提到。此外,还有纠缠集中协议[46-47],通过它可以在某些情况下增加纠缠量。以9-量子团簇态为信道,分别给出了两粒子态和三粒子态的双向隐形传态、双向制备以及传态与制备混合这三个不同类型的协议。在第一个协议中,Alice把自己的未知三量子态传递给Bob,同时Bob把自己的未知二量子态传送给Alice。其特点是方案中的GHZ-态测量基仅仅出现一部分可能的测量结果,这就大大简化了方案。在第二个协议中,Alice在遥远的Bob处制备了一个三量子已知态,Bob也能在Alice处制备一个已知二量子态。在双向制备过程中,充分利用了前馈测量策略,完美地完成任务。在第三个协议中,Alice将一个未知三粒子态传送给遥远的Bob,同时Bob也制备一个已知二量子态给远方的Alice。此方案吸取了前两个方案的优点,使得它既简单又高概率地完成量子任务。上述方案需要简化的三粒子策略、Bell测量、单量子测量、Hadamard门和Puali算子就能够以100%的概率重构原始二量子和三量子态。就目前的光学技术而言[5,11,30],本文所涉及的运算都能物理实现。
