矩阵迹最小问题的求解

谭 婕， 彭振赟

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

不定最小二乘问题

(1)

其中J=diag(Iq,-Iq)，Ip和Iq为单位矩阵，在总体最小二乘问题、几何近似和斜映射问题等的应用中具有十分重要的作用[1]。

对于不定最小二乘问题(1)，文献[2-4]利用QR分解、Cholesky分解方法给出了求解该问题的QR-Cholesky法和向后稳定法。文献[5-7]探讨了矩阵方程AXB=C有解的情况，给出了该矩阵方程通解的表达式。文献[8]利用双曲QR分解方法求解不定最小二乘问题，并验证了此方法比QR分解和Cholesky分解的运算量少，证明了双曲QR分解在条件较弱的情况下是向后稳定的，并对解的误差进行了分析，同时发展了这个问题的微扰理论，并确定了一个条件数。文献[9]介绍了广义双曲QR分解，并用该分解求解等式约束下的不定最小二乘问题，同时分析了有界误差。

矩阵迹最小问题

(2)

是不定最小二乘问题(1)的直接推广。2011年，欧阳君[10]首次提出问题(2)并给出了其有唯一解的充分必要条件，讨论了解的扰动分析。鉴于此，讨论矩阵迹最小问题(2)的更一般的矩阵迹最小问题，即矩阵迹最小问题

(3)

其中A∈Rm×n，B∈Rn×s,C∈Rm×s，m≥n，J=diag(Iq,-Iq),Ip和Iq为单位矩阵且p+q=m，得到矩阵迹最小问题(3)有唯一解的充分必要条件，给出解存在时解的计算方法与存在解时的算法，并通过数值例子验证求解问题(3)计算算法的可行性。

1 问题(3)有解的条件

引理1[1]设A∈Rm×n，rank(A)=n，m≥n，则有

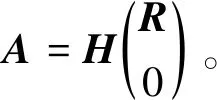
其中：R∈Rn×n为上三角非奇异矩阵；H∈Rm×m为J-正交矩阵，即HTJH=J。矩阵A的这种分解称为矩阵A的双曲QR分解。

引理2[11]设A∈Rm×n，rank(A)=r，m≥n>r，则有

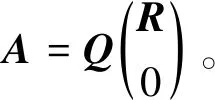
(4)

其中：R∈Rn×n为行满秩矩阵；Q为J-正交矩阵。

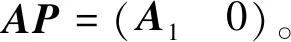
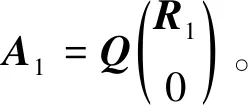
定理1问题(3)有解的充分必要条件是rank(A)=r≤p，有唯一解的充分必要条件是rank(A)=r=n≤p，且B满秩。

证明若rank(A)=r，则由引理2知，矩阵A可分解为式(4)。因此，有

(AXB-C)TJ(AXB-C)=

其中

R∈Rr×n，J=diag(Iq,-Iq).

若rank(A)=r≤p，则有

(AXB-C)TJ(AXB-C)=

(RXB-C1)T(RXB-C1)+C2J1C2。

(5)

其中J1=diag(Ip-r,-Iq)。因此，问题(3)等价于

(6)

因此，问题(3)有解。

反之，若rank(A)=r>p，则有

(AXB-C)TJ(AXB-C)=

(R1XB-C11)T(R1XB-C11)-

其中

因此，问题(3)等价于

(7)

做行满秩矩阵，对R1和R2的广义奇异值分解

其中：W为n可逆矩阵；U、V分别为p阶和r-p阶正交矩阵；C=diag(c1,c2,…,ct)>0；S=diag(s1,s2,…,st)>0；I为适当阶数的单位矩阵。令

X1∈R(p-t)×n,X2∈Rt×n,X3∈R(n-p-2t)×n,

则问题(3)等价于

(8)

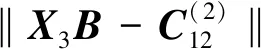
因为问题(3)有解时，其等价于问题(6)。而问题(6)有唯一解的充分必要条件为R、B为可逆矩阵。因此，问题(3)有唯一解的充分必要条件是rank(A)=r=n≤p，且B满秩。

2 求解问题(3)的解

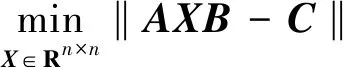
X=A+CB++W-A+AWBB+。

其中：‖A‖为矩阵A的Frobenius范数；W为任意矩阵。

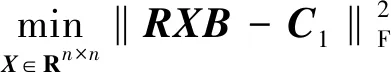
X=R+C1B++W-R+RWBB+，

(9)

其中W为任意矩阵。

证明由定理1的证明可知，问题(3)与问题(6)同解。由引理3知，问题(3)的解可表示为式(9)。

引理4[5]矩阵方程AXB=C的通解为

X=A-CB-+(I-A-A)U+V(I-BB-)。

其中：A-为矩阵A的g-广义逆；A+为矩阵A的Moore-Penrose广义逆，通常取A-=A+；U为任意矩阵。

定理3若问题(3)有解，则其与矩阵方程ATJAXBBT=ATJCBT同解，且其解可以表示为

X=A+JAA+JCB++

(I-A+JAA+JA)U+V(I-BB+)。

(10)

证明若问题(3)有解，则问题(3)的解即为矩阵方程ATJAXBBT=ATJCBT的解。

令F(X)=tr[(AXB-C)TJ(AXB-C)]，则有

F(X)=tr[(AXB)TJ(AXB)-(AXB)TJC-

CTJ(AXB)+CTJC]=tr(BTXTATJAXB)-

tr(BTXTATJC)-tr(CTJAXB)+tr(CTJC)。

对F(X)求导，有

对F(X)二次求导，有

由于问题(3)有解，则有rank(A)=r≤p，从式(5)可知，ATJA>0。又因BBT>0，可得F″(X)>0，故F(X)为凸函数。因此，矩阵方程ATJAXBBT=ATJCBT的解即为问题(3)的解，则问题(3)的解等价于矩阵方程ATJAXBBT=ATJCBT的解。

由引理4可知，问题(3)的解为

X=(ATJA)-ATJCBT(BBT)-+

(I-(ATJA)-ATJA)U+V(I-BBT(BBT)-)=

A-J(A-)TATJCBT(B-)TB-+

(I-A-J(A-)TATJA)U+

V(I-BBT(B-)TB-)=

A+J(AA+)TJC(B+B)TB++

(I-A+J(AA+)TJA)U+

V(I-B(B+B)TB+)=

A+JAA+JCB++(I-A+JAA+JA)U+

V(I-BB+)。

3 数值算例

由定理2、3可得如下2种求解问题(3)的不同算法。

算法1(根据定理2求解问题(3)的算法)

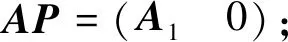
2)由引理1将矩阵A1进行双曲QR分解，得Q、R1；

3)从

可得R；

4)计算

其中C1∈Rr×n，C2∈R(m-r)×n；

5)求矩阵R、B的广义逆R+、B+；

6)将R+、B+、B、R、C代入式(9)，求得问题(3)的解。

算法2(根据定理3求解问题(3)的算法)

1)A为降秩，将A分解成A=A1M，其中A1为列满秩，M为行满秩；

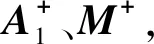
3)求矩阵B的广义逆B+；

4)将A、B、A+、B+、C、J代入式(10)，求得问题(3)的解。

例取m=8，n=7，p=5，q=3，随机给出矩阵：

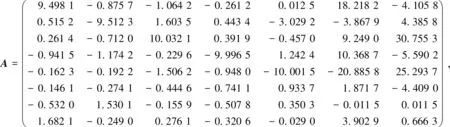
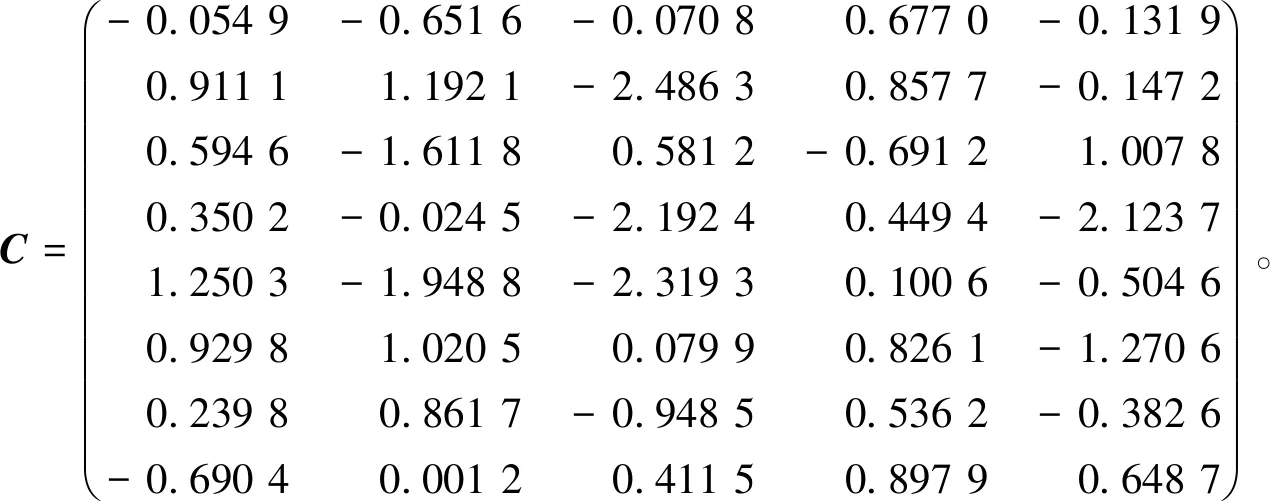
其中J=diag(I5,-I3)，I5和I3为单位矩阵。

通过算法1的计算，可得

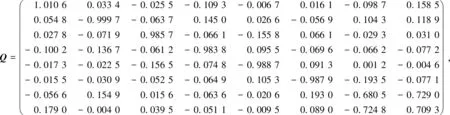
假设W为单位矩阵，将R+、B+、B、R、C代入式(9)，可求得问题(3)的解：

(11)

且当X为式(11)时，tr[(AXB-C)TJ(AXB-C)]=-8.795 8。

将A、B、A+、B+、C、J代入式(10)中，假设U、V为单位矩阵，从而可得问题(3)的解：

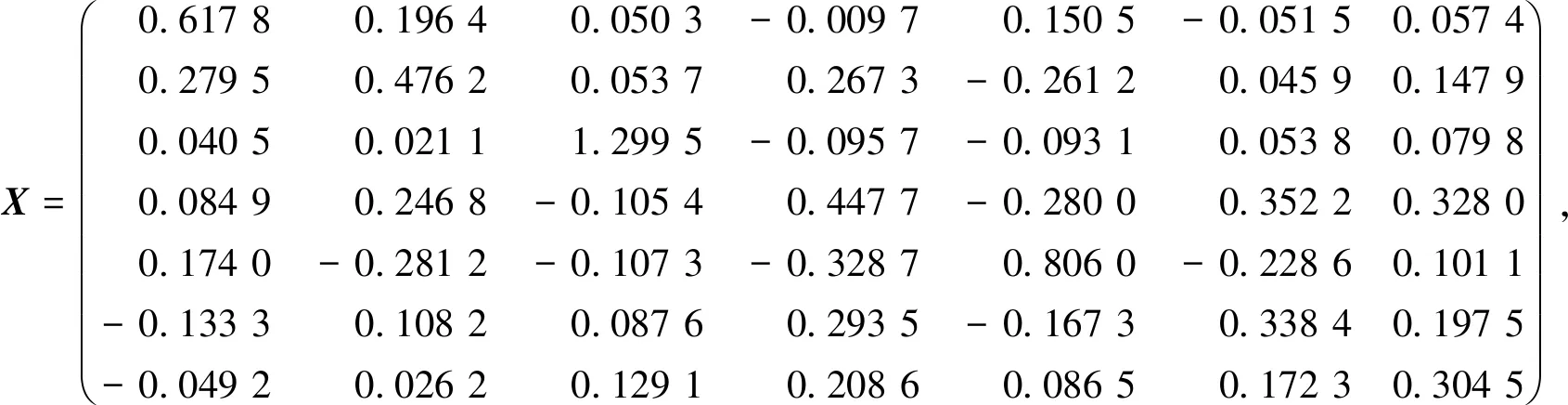
(12)

且当X为式(12)时，tr[(AXB-C)TJ(AXB-C)]=95.416 6。

4 结束语

利用双曲QR分解方法分析了一类矩阵迹最小问题有解、有唯一解的充分必要条件，并通过该方法将矩阵迹最小问题转化成最小二乘问题，同时结合矩阵理论给出一类矩阵迹最小问题的解存在时解的计算方法。数值实验表明，该方法可行。