非线性多智能体系统在脉冲控制下的部分分量一致性
2019-09-11刘鹏飞马忠军
刘鹏飞, 马忠军
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.桂林电子科技大学 广西高校数据分析与计算重点实验室,广西 桂林 541004)
近年来,随着人工智能技术的不断提升,多智能体协调控制在数学、生物学和通信控制等领域引起了众多学者的研究兴趣。一致性作为多智能体协调控制的根本问题之一,在耦合振子系统同步[1]、多机器人编队[2]、通信网络拥塞[3]和群集[4]等领域有着广泛应用。一致性是指在控制协议下,多智能体的状态变量(如位置、速度)与系统随时间的演化达到渐近相同。
连续控制和非连续控制[5-12]构成了一致性协议中的主要内容。其中,脉冲控制作为一致性协议中的一类非连续控制方法,具有非连续性、瞬时性、低耗能性、较强的鲁棒性以及抗干扰能力等优点,已被广泛应用于各种动力系统[13-19]。文献[13]首次给出了脉冲控制的概念;文献[14]提出了一种新的离散时刻多智能体系统的脉冲控制方法;文献[15]针对非线性多智能体系统的时滞脉冲控制问题,利用脉冲控制理论解决了状态依赖时滞脉冲微分系统的局部稳定性问题;文献[16]通过给出一个新的李雅普诺夫函数,建立了在任意条件下脉冲切换的指数稳定性和渐近稳定性的一般准则;文献[17]考虑了切换拓扑下的非线性多智能体系统的二阶一致性问题;文献[18]运用矩阵不等式和脉冲算法研究了具有非线性时变时滞的多智能体系统的二阶一致性问题;文献[19]研究了具有随机时变时滞和非线性扰动的多智能体系统的三阶一致性问题,以线性矩阵不等式(LMIs)的形式给出了实现滞后一致性的几个充分条件。
在上述研究中考虑的一致性是在脉冲控制下,多智能体的所有状态变量(如位置或速度)趋于渐近一致。文献[20]从另外的角度,针对一阶非线性多智能体系统,提出了部分分量一致性的概念,并给出了多智能体部分分量一致性的充分条件。但关于脉冲控制在部分分量一致性的应用尚处于空白阶段。鉴于此,给出并证明了脉冲微分系统的部分变分稳定性定理,研究了一阶非线性多智能体系统在脉冲控制下部分分量的一致性,利用图论、矩阵范数理论和脉冲微分方程理论,通过设计适当的脉冲控制项和选择合适的脉冲区间,得到了多智能体系统达到部分成分一致性的充分条件。数值模拟验证了理论结果的正确性和有效性。
1 预备知识
考虑如下脉冲微分系统[21]
(1)
其中,
x=(y,z)=(x1,x2,…xm,xm+1,…,xn)T∈Rn,
首先给出如下假设:
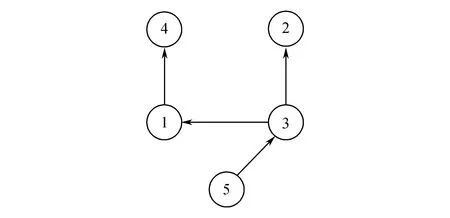
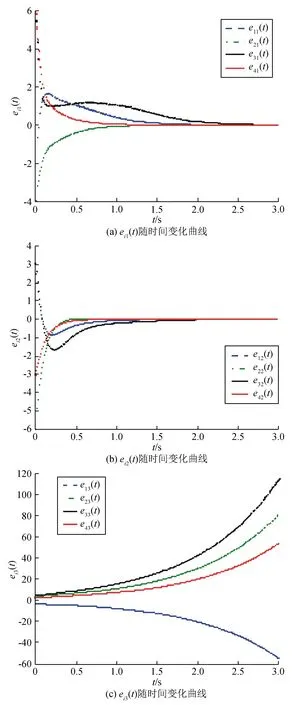
H1 0 时,tk→+∞; H2 函数f:R+×Rn→Rn在(tk-1,tk]×Rn连续,且对任意x∈Rn,k∈Z+, 存在; H3Ik:Rn→Rn。 引理1[19]设V:R+×Rn→R+,V是正定的,假设 (2) 其中,g:R+×R+→R是连续的,且ψk:R+→R+单调不减。若r(t)=r(t,t0,u0)为纯量脉冲微分系统, (3) 定义在[t0,+∞)上的最大解,那么若 则有 V(t,x(t))≤r(t),t≥t0, (4) 其中x(t)=x(t,t0,x0)为系统(1)定义在[t0,+∞)上的任意解。 H4V∈C(R+×S(ρ),R+), D+V(t,x)≤g(t,V(t,x))(t≠tk); H5 存在ρ0>0,x∈S(ρ0),使得 x+Ik(x)∈Sρ0, 且 V(t,x+Ik(x))≤ψk(V(t,x)),t=tk, 对所有的k都成立; H6b(‖y‖)≤V(t,x)≤a(‖x‖),其中a,b∈K。 定理1若满足以上3个假设,则系统(1)的平凡解关于部分变元y的稳定性与系统(3)的稳定性一致。 证明过程类似于参考文献[21]中的方法。 证明任意给定0<ε<ρ0,t0∈R+,假设系统(3)的解是稳定的,则给定b(ε)>0,存在δ1(t0,ε)>0,使得当0≤u0<δ1时,有u(t,t0,u0) 1)取δ=min{δ1,δ2},用反证法证明,若‖x0‖≤δ,则当t≥t0时,‖y(t)‖<ε。 若上述不正确,则系统(1)存在解 x(t)=(y(t),z(t)),‖x0‖<δ 和t*>t0,使得对某个k当tk ε≤‖y(t*)‖和‖y(t)‖<ε(t0≤t≤tk)。 由于0<ε<ρ0,且条件H5表明 可以找到一个t0,使得当tk ε≤‖y(t0)‖≤‖x(t0)‖<ρ0。 记m(t)=V(t,x(t)),t0≤t V(t,x(t))≤r(t,t0,a‖x0‖),t0≤t (5) 其中r(t,t0,u0)为系统(3)的最大解。由条件H6可得如下矛盾: b(ε)≤b(‖y(t0)‖)≤V(t0,x(t0))≤ r(t0,t0,a‖x0‖) (6) 故系统(1)的平凡解关于y稳定。 2)证明系统(3)的解u≡0是渐近稳定的,则系统(1)的平凡解关于y也是渐近稳定的。 ‖y(t)‖<ρ0,t≥t0。 (7) V(t,x(t))≤r(t,t0,a‖x0‖),t≥t0, 于是有 b(‖y(t)‖)≤V(t,x(t))≤r(t,t0,a‖x0‖)< b(ε),t≥t0+T。 (8) 故‖y(t)‖<ε。因此系统(1)的平凡解关于y是渐近稳定的。 将脉冲微分系统的部分变元稳定性理论应用到多智能体系统中,考虑一阶非线性脉冲控制系统 (9) xi(t))-diΓ(xi(t)-x0(t))]。 (10) 其中:k∈N+,i=1,2,…,N;δ(t)为Dirac函数;c>0为耦合强度;Γ=diag(r1,r2,…,rn)∈Rn×n,rk≥0,k=1,2,…,n为内部耦合矩阵。若第i个智能体可以接收第j智能体的信息时,aij>0,否则aij=0。当第i个智能体能接收到领导者的信息时,di>0,否则di=0。设领导者的状态方程为 (11) 其中:x0=(x01,x02,…,x0n)∈Rn为领导者的状态;f(x0)为非线性连续函数。设 ei(t)=xi(t)-x0(t),i=1,2,…,N。 当t≠tk时,误差系统为 (12) 矩阵形式为 (13) 其中 F(x(t))=g(x(t),t)-1N⊗f(x0(t),t), g(x(t),t)=[fT(x1(t),t),fT(x2(t),t),…, fT(xN(t),t)]T。 当t=tk时,由式(9)、(10)可得 (14) 矩阵形式为 (15) 其中D=diag(d1,d2,…,dN)。 为了研究误差系统(16)和(17)的平凡解的部分变元的渐近稳定性,参考文献[20]中的变换,令 计算可得 k=1,2,…,n, 因此式(13)、(15)可转化为: 当t≠tk时,误差系统为 (16) 其中, f1(xN))T,…,(f2(x1),f2(x2)…,f2(xN))T, (fn(x1),fn(x2)…,fn(xN))T]T。 当t=tk,误差系统为 (17) (18) 其中,α>0, H8 矩阵 [InN×Nn-cΓ⊗(L+D)]TW[InN×Nn- cΓ⊗(L+D)] 半正定,且最大特征值λmax<1,谱范数 ‖InN×Nn-cΓ⊗(L+D)‖2≤1; H9 脉冲时间间隔满足 0<β1≤tk+1-tk≤β2<+∞; 定义1[20]若存在1≤l≤n,使得式(9)、(11)的解满足 则称式(9)、(11)关于前l个分量达到部分分量一致。 定理2若式(9)、(11)满足H7~H10,则在脉冲控制协议下的多智能体系统关于前l个分量达到部分分量一致。 其中, y=(e11(t),e12(t)…,e1l(t), eN1(t),eN2(t),…,eNl(t))T。 显然,a,b∈K,构造如下李雅普诺夫函数: 其中, 因此,函数V(t)满足定理1中H6的条件 b(‖y‖)≤V(t,x)≤a(‖x‖)。 当t∈(tk-1,tk]时,取Dini导数有 取 则误差比较系统为 (19) 对于该脉冲微分方程,易解得: (20) 因此, (21) 由定理条件 可得 通过给出一个数值例子来验证所提脉冲控制协议算法的有效性。 例1设有4个网络节点,每个节点取3维系统,考虑多智能体系统关于前2个分量的一致性问题,网络拓扑图为含有向生成树图,如图1所示。 图1 含有向生成树拓扑图 令第i个智能体的状态方程为 通过计算,取α=2时假设成立。取L、D分别为 取 Γ=diag(1,1,0),c=0.1, 则最大特征值为λmax=0.966 8。为方便计算,取等脉冲间隔Δ=tk+1-tk=0.01,则其满足定理2条件。 图2 系统误差变量eij(t)的演化过程 通过Matlab软件得到误差轨迹随时间t的演化如图2所示。图2(a)与图2(b)表明,所有智能体的前2个分量都能达到一致,而图2(c)表明另一个分量未达到一致。因此,提出的脉冲控制协议在部分分量一致性中的应用是有效的。 提出了一种脉冲微分系统部分变元稳定性定理并给予证明,并研究了一阶非线性多智能体系统部分分量在脉冲控制下的一致性。采用适当的脉冲间隔、矩阵理论和稳定性理论,通过设计合适的脉冲控制项,得到了多智能体系统部分分量一致性的充分条件。数值模拟验证了理论结果的正确性。本研究仅考虑了对位移直接进行脉冲控制得出前l个分量的一致性,在接下来的工作中,将研究二阶多智能体系统在脉冲控制下的部分分量一致性问题。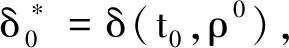
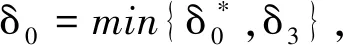
2 主要结果
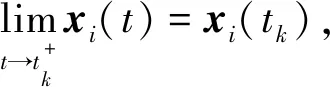
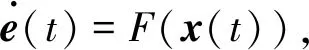
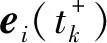
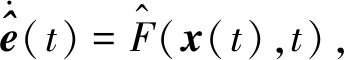
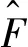
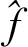
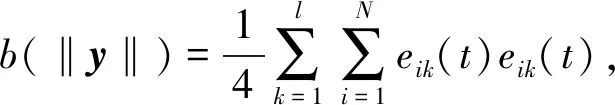
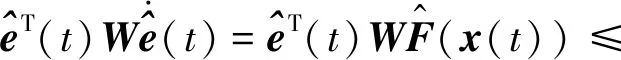
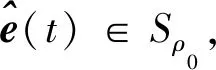


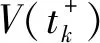

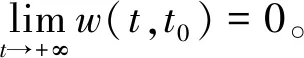
3 数值模拟

4 结束语
