基于多项式拟合对煎炸油质量的预测

解久莹,吉静筠,李裕梅,杨雪莲,*,曹雁平,*

(1.北京市食品营养与人类健康高精尖创新中心,北京工商大学食品学院,北京 100048;2.北京工商大学食品学院,食品质量与安全北京实验室,北京 100048;3.北京工商大学理学院,北京 100048)

由于煎炸食品诱人的风味、酥脆的口感、良好的造型和色泽以及丰富的后味因而深受消费者的喜爱,但是当煎炸温度过高、煎炸时间过长时,煎炸油会发生多种物理、化学变化,并渗入食物成为其组成成分,对食物品质和营养价值产生影响。

传统的检测油脂质量的理化指标如酸价、羰基价、极性组分等在测量过程中存在费时费力,消耗大量化学试剂,对环境也会产生一定的影响。而多项式拟合建模法是通过离散的部分数据点推测出函数关系再通过函数关系反推任意时间点的化学指标值,具有操作简便、省时省力、快速预测的优点。

目前,多项式拟合主要应用在能源优化[1]、用电能耗[2]、煤矿事故[3]、发病率预测[4]、股票拐点[5]等领域中,通过建模对煎炸油判废国内外研究均较少。国标法对煎炸油质量的判废标准主要是依据酸价≥5 mg KOH/g、羰基价≥50 meq/kg、极性组分≥27%。煎炸油质量的好坏将直接影响到油炸食品的质量安全与消费者的健康。通过控制煎炸油的品质,可以保证油炸食品的品质。因此本文提出了一种基于多项式拟合的煎炸油脂实时质量预测的方法,通过测定酸价、羰基价、极性组分等三个理化指标数据,进行多项式拟合建模,在初次拟合模型的基础上,剔除异常数据并用剔除异常后剩下的数据再次进行多项式拟合建模,用得到的模型去预测其他未知时间点的理化指标的值。经过多次验证实验,证明该方法有效可行。

1 材料与方法

1.1 材料与仪器

大豆油 中粮东海粮油工业(张家港)有限公司;速冻薯条 上海圣方实业有限公司;氢氧化钠、乙醚、异丙醇、乙醇、三氯乙酸、苯、氢氧化钾、石油醚 北京化工厂;酚酞指示剂 天津市北辰方正试剂厂;2,4-二硝基苯肼 天津市瑞金特化学品有限公司。

HH-S数显恒温油浴 常州荣华仪器制造有限公司;HH-ZK1恒温水浴锅 巩义市予华仪器责任有限公司;球形冷凝管、玻璃干燥器 北京化玻站生物分析技术有限公司;UV-9000S型双光束紫外可见分光光度计 上海元析仪器有限公司;YZF真空干燥箱 上海姚氏仪器设备厂。

1.2 实验方法

1.2.1 煎炸油样的制备 设定温度分别为(160±2)、(175±2)、(190±2)、(205±2)、(220±2) ℃,在每个温度下,将15 L大豆油倒入恒温煎炸锅中进行煎炸油样的制备,每天连续煎炸,共煎炸30 h,每一个煎炸温度在煎炸过程中保持油温相同,每小时煎炸六份薯条(每份薯条质量为100～200 g),每份薯条采用3 min煎炸,7 min恒温的煎炸工艺。从0 h开始,每小时取150 mL油样冷却至室温,滤去沉淀后存储于样品瓶中,-20 ℃存放以备各个理化指标的测定,每个温度取31个油样,共取155个油样。

1.2.2 酸价(AV)含量测定值 参照GB/T 5009.37-2003《食用植物油卫生标准的分析方法》[6]的测定方法,获取155个大豆油样品的AV含量的测定值。

1.2.3 羰基价(CV)含量测定值 参照GB/T 5009.37-2003《食用植物油卫生标准的分析方法》[6]的测定方法,获取155个大豆油样品的CV含量的测定值。

1.2.4 极性组分(PC)含量测定值 参照GB/T 5009.202-2016《食用油中极性组分(PC)的测定》[7]的测定方法,获取155个大豆油样品的PC含量的测定值。

1.3 多项式拟合原理

多项式拟合又称为最小二乘拟合[8-9],常用于把离散的数据归纳总结为连续的函数。多项式拟合具体过程如下:

本文在进行多项式拟合时,定义该曲线满足如下约束:

y=f(x)=a0+a1x+a2x2+…+anxn

式(1)

式中:ai表示该多项式的系数;n表示该多项式的次数。

对式(1)中的多项式的系数求解时,采用最小二乘法求解使得I的取值为最小:

式(2)

首先,I对每个系数ai进行求导可以得出一个方程组:

式(3)

将式(3)转化为矩阵形式:

式(4)

化简式(4)得:

式(5)

用矩阵向量的形式表示式(5),得

XM=Y

式(6)

M即为所求的系数矩阵,则

式(7)

使用多项式拟合的一般方法可以归纳为:

a、由已知数据画出函数粗略的图形(散点图),确定拟合多项式的次数n;

b、列表计算实际值与拟合值直接的关系;

c、写出正规方程组,求出多项式中各项系数a;

1.4 删除学生化残差原理

1.5 Cook距离原理

Cook(库克)距离是用来判断强影响点是否为y的异常值点。

计算公式如下:

式(8)

Cook距离反映杠杆值hii与残差ei大小的一个综合效应。当Di<0.5时,认为不是异常值点;当Di>1时,认为是异常值点[11]。

1.6 数据处理

各个理化指标均测量三次取平均值。使用Matlab软件进行数据处理。在每个温度下,将每个理化指标的数据与煎炸时间进行多项式拟合,通过残差计算决定多项式的次数,通过判决系数R2判断拟合模型的优度,R2越接近1,表明拟合优度越高。通过计算各温度下数据在拟合后的删除学生化残差和Cook距离,当某个数据对应删除学生化残差的绝对值>3或Cook距离>1时,表明数据异常,需要剔除。初次拟合剔除异常数据后,再次进行多项式拟合,直到得到最优模型。

2 结果与分析

2.1 160 ℃下三个指标的散点图及拟合情况

在160 ℃条件下进行煎炸实验,获得各理化指标的散点图,进行初次拟合,找到删除学生化残差绝对值>3或者Cook距离>1的异常数据进行剔除,并用剔除异常后剩下的数据再次做多项式拟合建模,得到160 ℃条件下的结果如图1所示,160 ℃各理化指标的回归方程如表1所示。

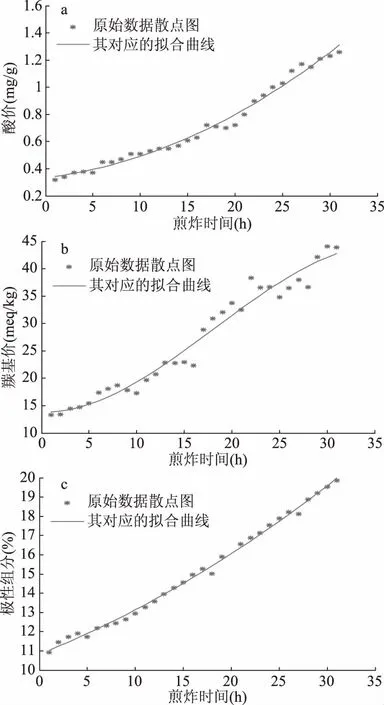
图1 160℃三个理化指标的散点图及拟合曲线Fig.1 Scatter plots and fitting curves of three physical and chemical indicators at 160 ℃注:a:160 ℃酸价散点图及拟合曲线;b:160 ℃羰基价散点图及拟合曲线;c:160 ℃极性组分散点图及拟合曲线。

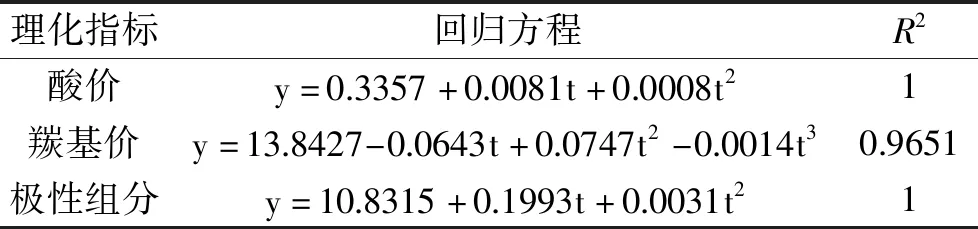
表1 160 ℃各理化指标的回归方程Table 1 Regression equations for physical and chemical indicators at 160 ℃

通过残差和Cook距离分析,三个理化指标的数据均无异常值。由图1a可知,曲线大致呈二次,在10～20 h期间测量值与拟合曲线距离较远,可能是由于人为添加滴定液造成的误差,或者取样时间提前导致酸价略有降低,其他部分拟合良好;由图1b可知,曲线大致呈三次,整个实验期间测量值始终分布在拟合曲线两侧,可能是由于在煎炸过程中油脂劣变速率不同从而产生的误差;而图1c中曲线表面上看像一次,但是也为二次曲线,只不过二项式系数较小接近0,在实验过程中没有产生异常值,散点图与其对应的拟合曲线拟合良好。由表1可知,三个指标在进行拟合后R2均接近或等于1,拟合效果较好。在160 ℃条件下,因煎炸30 h后三个理化指标均还在国标范围内,因此继续煎炸,直到煎炸至第34 h时羰基价已经超过国标规定的≥50 meq/kg,虽然酸价和极性组分还没有达到国标的废弃点,但此时此油已经发生劣变不宜食用。

2.2 175 ℃下三个指标的散点图及拟合情况

在175 ℃条件下进行煎炸实验,获得各理化指标散点图,进行初次拟合,找到删除学生化残差绝对值>3或者Cook距离>1的异常数据进行剔除,并用剔除异常后剩下的数据再次做多项式拟合建模,得到175 ℃条件下的结果如图2所示,175 ℃各理化指标的回归方程如表2所示。

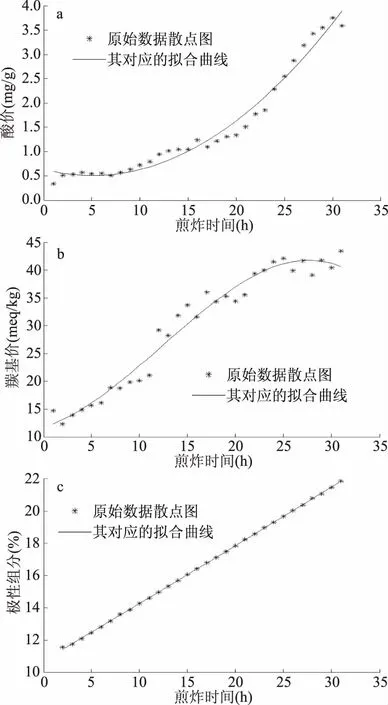
图2 175℃三个理化指标的散点图及拟合曲线Fig.2 Scatter plots and fitting curves of three physical and chemical indicators at 175 ℃注:a:175 ℃酸价散点图及拟合曲线;b:175 ℃羰基价散点图及拟合曲线;c:175 ℃极性组分散点图及拟合曲线。

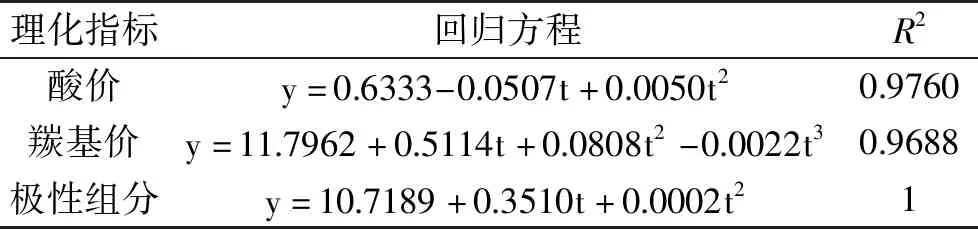
表2 175 ℃各理化指标的回归方程Table 2 Regression equations for physical and chemical indicators at 175 ℃

通过残差和Cook距离分析,酸价和羰基价的数据均无异常值,极性组分剔除了第1 h的数据。由图2a可知,曲线大致呈二次,在10～12 h、19～22 h期间测量值与拟合曲线距离较远,可能是由于人为添加滴定液造成的误差,其他部分拟合良好;由如图2b可知,看似二次曲线,实际为三次曲线,三次项系数较小。在14～30 h期间测量值与拟合曲线距离较远,可能是由于人为取样质量不同以及操作过程中产生的误差,其他部分拟合良好;而图2c中曲线大致呈一次,散点图与其对应的拟合二次曲线几乎完全一致,拟合良好。由表2可知,三个指标在进行拟合后R2均接近或等于1,拟合效果较好。直到煎炸到第30 h,三个理化指标均没有超过国标规定的值,因此,可以继续进行煎炸。

2.3 190 ℃下三个指标的散点图及拟合情况

在190 ℃条件下进行煎炸实验,获得各理化指标散点图,进行初次拟合,找到删除学生化残差绝对值>3或者Cook距离>1的异常数据进行剔除并用剔除异常后剩下的数据再次做多项式拟合建模得到190 ℃条件下的结果如图3所示,190 ℃各理化指标的回归方程如表3所示。

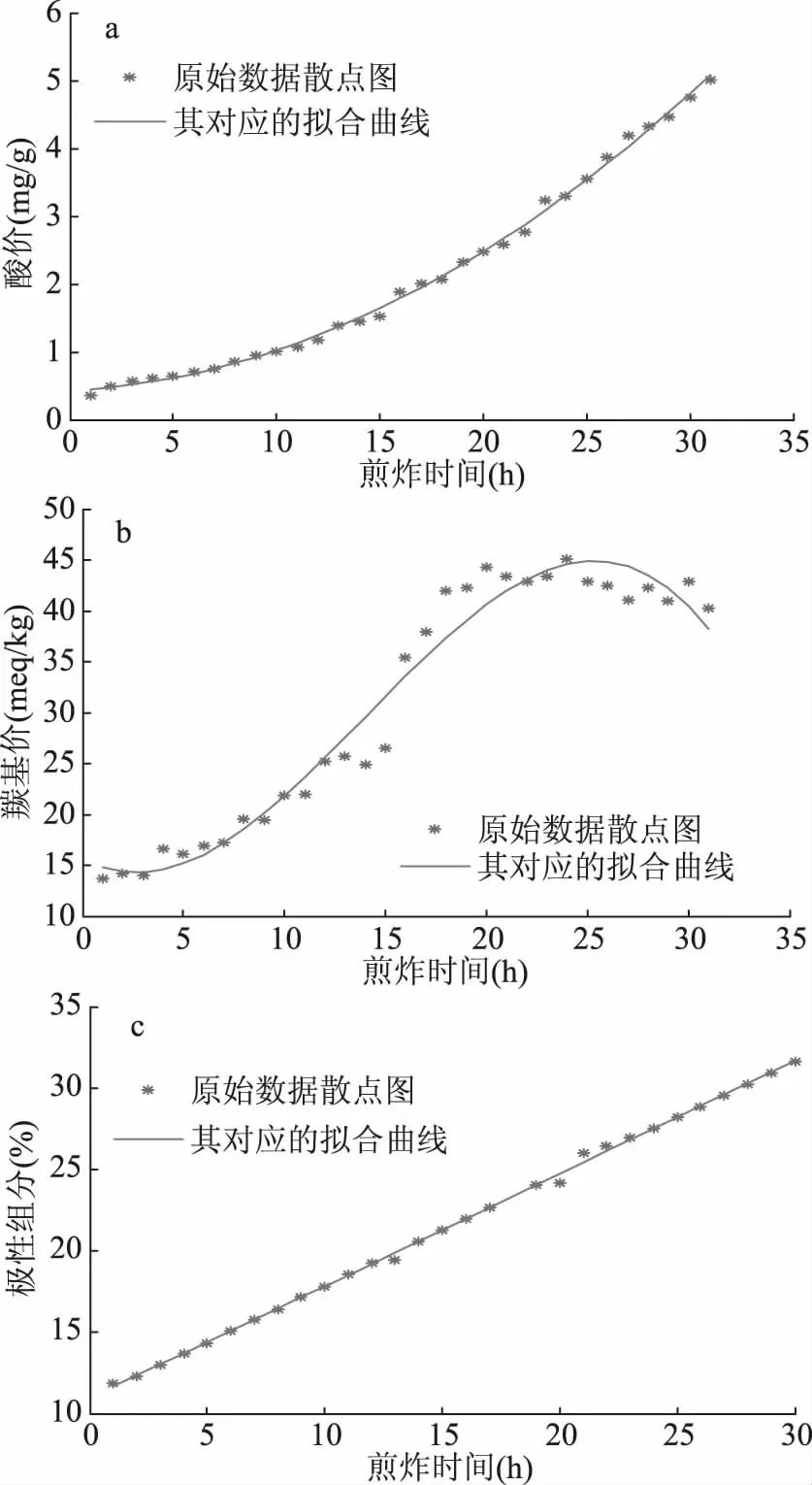
图3 190℃三个理化指标的散点图及拟合曲线Fig.3 Scatter plots and fitting curves of three physical and chemical indicators at 190 ℃注:a:190 ℃酸价散点图及拟合曲线;b:190 ℃羰基价散点图及拟合曲线;c:190 ℃极性组分散点图及拟合曲线。

表3 190 ℃各理化指标的回归方程Table 3 Regression equations for physical and chemical indicators at 190 ℃

通过残差和Cook距离分析,酸价和羰基价的数据均无异常值,极性组分剔除了第17 h、30 h的数据;由图3a可知,曲线大致呈二次,0～30 h期间测量值与拟合曲线均很接近,拟合良好;由图3b可知,曲线呈三次,13～19 h期间测量值与拟合值距离较远,可能是由于人为取样质量不同以及操作过程中产生的误差,其他部分拟合良好;而图3c中曲线呈不明显的二次曲线,散点图与其对应的拟合曲线除19 h附近的几个点之外几乎完全一致,R2=1,拟合良好。

在190 ℃条件下,煎炸第23 h时极性组分已经超过国标规定的27%,煎炸第30 h羰基价和酸价已经超过国标规定的50 meq/kg和5 mg/g。因此应在煎炸第23 h废弃本批煎炸油。

2.4 205 ℃下三个指标的散点图及拟合情况

在205 ℃条件下进行煎炸实验,获得各理化指标散点图,进行初次拟合,找到删除学生化残差绝对值>3或者Cook距离>1的异常数据进行剔除并用剔除异常后剩下的数据再次做多项式拟合建模得到205 ℃条件下的结果如图4所示,通过删除学生化残差和Cook距离判断数据异常情况,极性组分205 ℃数据通过初始拟合算出删除学生化残差和Cook距离数据如下表4所示,205 ℃各理化指标的回归方程如表5所示。

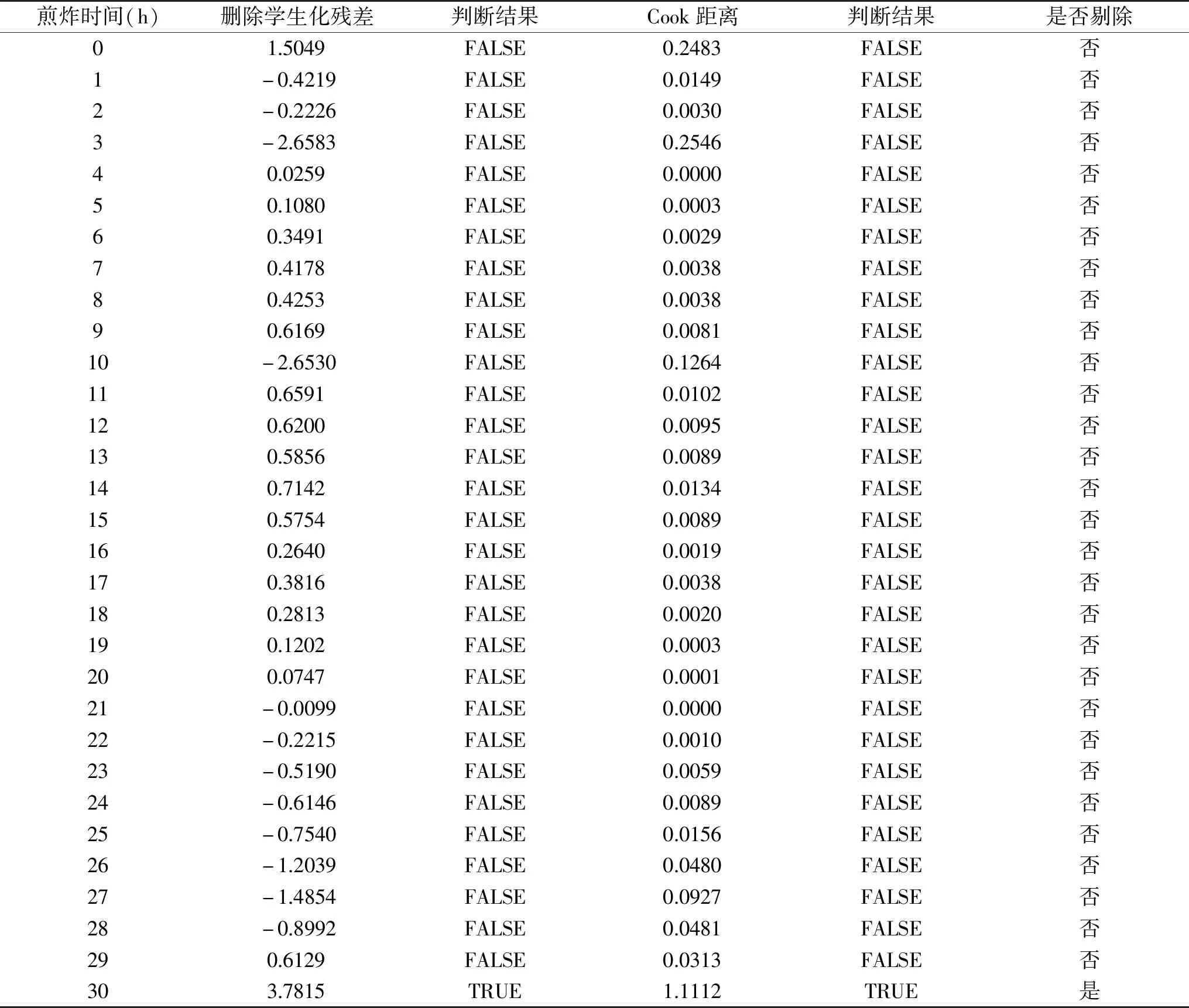
表4 羰基价205 ℃删除学生化残差和Cook距离及其异常判断结果Table 4 Carbonyl value of 205 ℃ delete studentized residuals and Cook distance and its abnormal judgment results

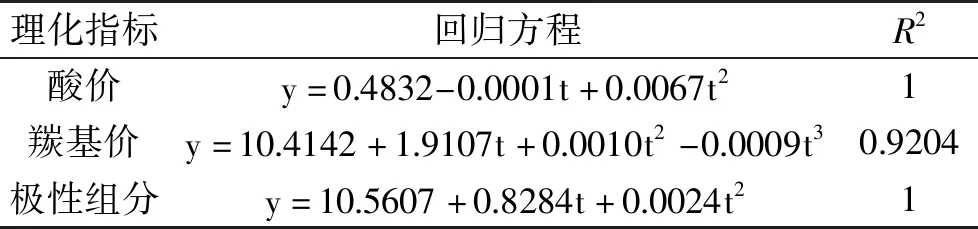
表5 205 ℃各理化指标的回归方程Table 5 Regression equations for physical and chemical indicators at 205 ℃

图4 205℃三个理化指标的散点图及拟合曲线Fig.4 Scatter plots and fitting curves of three physical and chemical indicators at 205 ℃注:a:205 ℃酸价散点图及拟合曲线;b:205 ℃羰基价散点图及拟合曲线;c:205 ℃极性组分散点图及拟合曲线。

通过残差和Cook距离分析,酸价和羰基价数据均无异常值,极性组分剔除了第30 h的数据。由图4a可知,曲线大致呈二次,在整个测试期间测量值与拟合曲线均很接近,R2=1,拟合良好;由图4b可知,曲线看似为二次曲线,实则为三次曲线,只不过三次项系数较小。在整个测试期间测量值始终分布在拟合曲线两侧,但测试值距离拟合曲线较远,导致残差平方和在羰基价5个温度梯度中也最大,达到286.8074,但从R2来看,数值较为接近1,拟合良好;图4c中曲线呈不明显的二次曲线,剔除了唯一的一个异常值第30 h的数据后,除3 h和11 h外,散点图与其对应的拟合曲线几乎完全重合,R2接近1,拟合良好。在205 ℃条件下,煎炸第18 h时极性组分已经超过国标规定的27%,煎炸第25 h酸价已经超过国标规定的5 mg/g,煎炸第29 h羰基价已经超过国标规定的50 meq/kg。因此应该在煎炸第18 h废弃本批油脂。

2.5 220 ℃下三个指标的散点图及拟合情况

在220 ℃条件下进行煎炸实验,获得各理化指标散点图,进行初次拟合,找到删除学生化残差绝对值>3或者Cook距离>1的异常数据进行剔除并用剔除异常后剩下的数据再次做多项式拟合建模得到220 ℃条件下的结果如图5所示,220 ℃各理化指标的回归方程如表6所示:

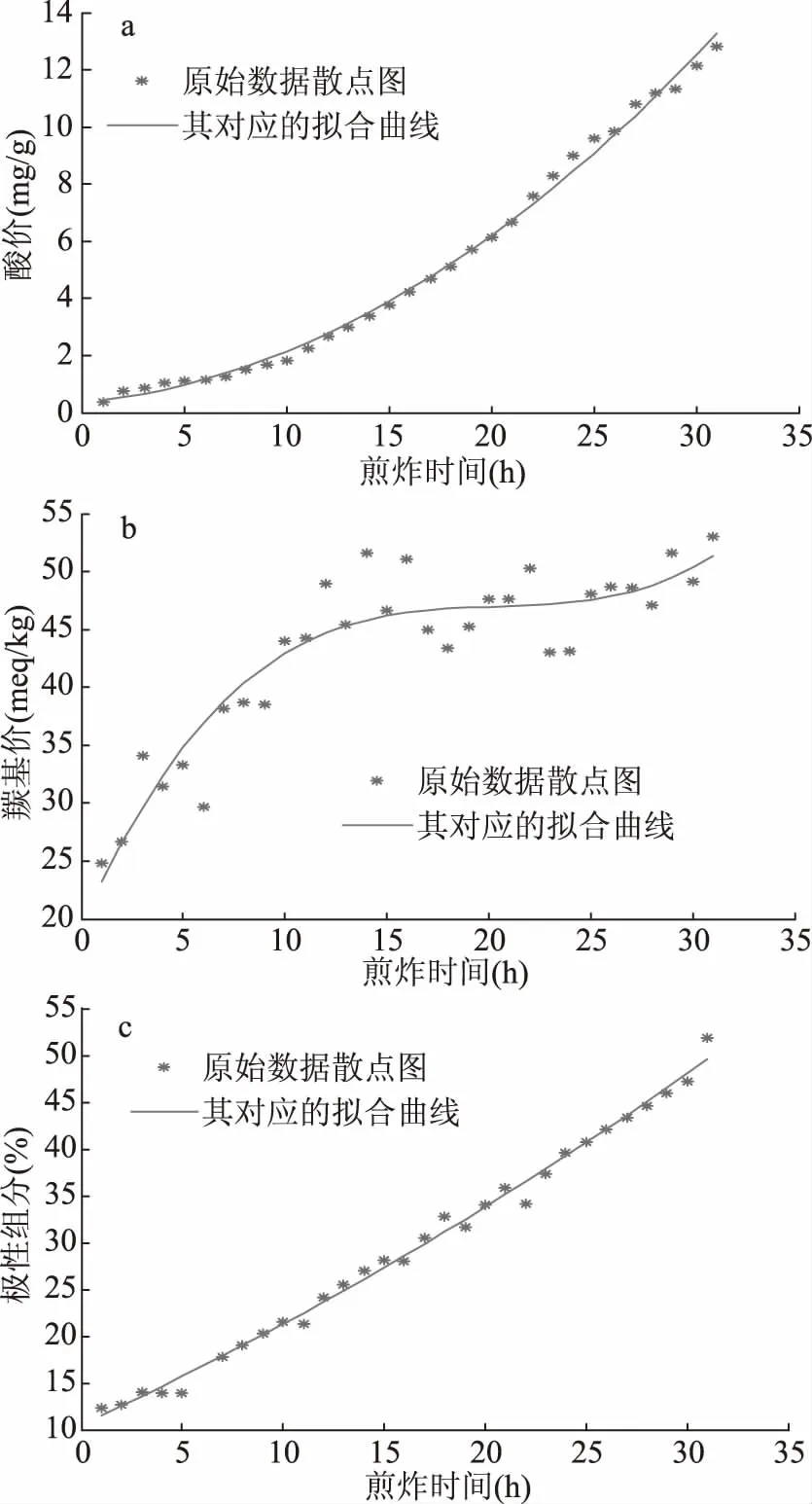
图5 220℃三个理化指标的散点图及拟合曲线Fig.5 Scatter plots and fitting curves of three physical and chemical indicators at 220 ℃注:a:220 ℃酸价散点图及拟合曲线;b:220 ℃羰基价散点图及拟合曲线;c:220 ℃极性组分散点图及拟合曲线。

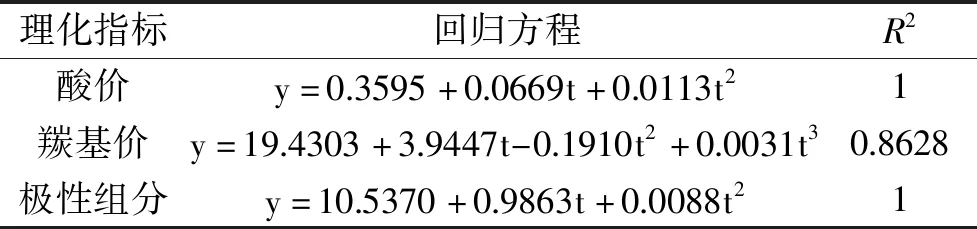
表6 220 ℃各理化指标的回归方程Table 6 Regression equations for physical and chemical indicators at 220 ℃

通过残差和Cook距离分析,酸价和羰基价的数据均无异常值,极性组分剔除了第5 h的数据,由图5a可知,曲线呈二次,在整个测试期间测量值与拟合曲线均很接近;由图5b可知,曲线呈三次,且在整个测试期间测量值始终分布在拟合曲线两侧,测量值与拟合值差距较大导致残差平方和较大,而且R2较低,但仍高于0.85,因此拟合效果较好。图5c中曲线呈不明显的二次曲线,剔除了第5 h的数据后,测量值如第4、19、29 h数据依旧距离拟合曲线较远导致残差平方和在5个温度下极性组分的实验中最大,达到25.8455。但在拟合后,R2=1,实现了较完美的拟合。在220 ℃条件下,煎炸第13 h时极性组分已经超过国标规定的27%,煎炸第17 h时酸价已经超过国标规定的5 mg/g,煎炸第24 h时羰基价已经超过国标规定的50 meq/kg。因此应在煎炸第13 h废弃本批油脂。

2.6 残差平方和

下面将计算出的三个理化指标实际测量数据值和相应回归方程预测值之间的残差平方和展现在图6中:

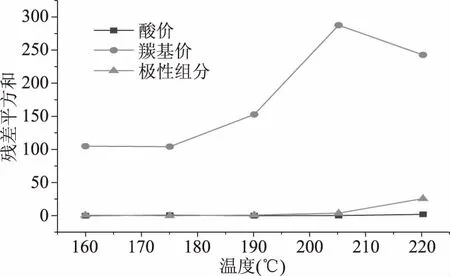
图6 三个理化指标的残差平方和Fig.6 The sum of squared residuals of three physical and chemical indicators

在拟合过程中,羰基价的残差平方和数值始终大于其他两个指标,可能是因为人为操作的差异或所量取油脂质量的不同导致的,也可能是因为油脂劣变速率不同,在羰基价这个指标上反映明显。只有在220 ℃时极性组分的残差平方和比较大,也是油脂劣变速率不同所导致的结果。只有酸价的残差平方和较稳定且较小,且在测量时变化也较均匀,因此酸价这个指标对于油脂的劣变情况反映不明显。

2.7 验证实验

重新煎炸一批样品,随机在160 ℃下取3.5、8.17、17.67 h;175 ℃下取15.25、21.67、29.08 h;190 ℃下取6.17、14.83、27.33 h;205 ℃下取4.17、16.33、22.83 h;220 ℃下取8.33、18.83、26.33 h等15个样品进行酸价,羰基价,极性组分的检测,并与拟合值进行对比,结果如表7～表9。

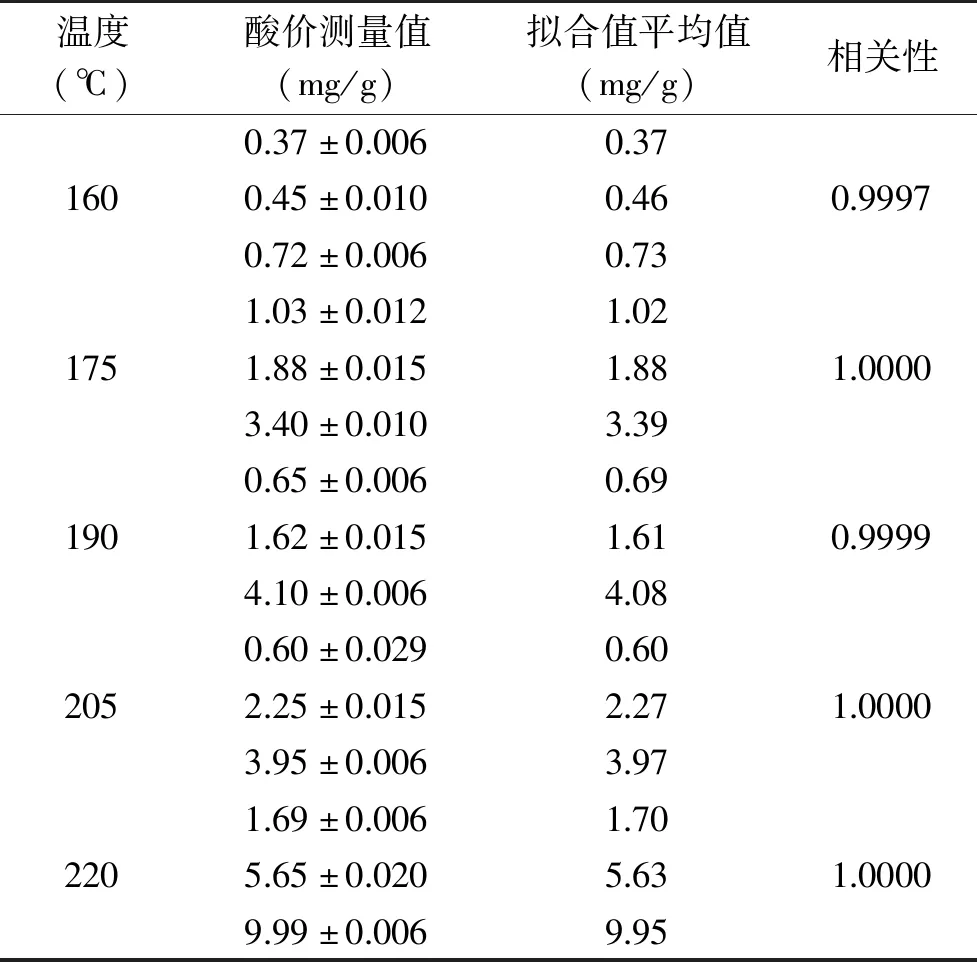
表7 各温度梯度酸价的模型验证Table 7 Model verification of acid value for each temperature gradient

由表7可知,五个温度梯度下样品的酸价的测量值与拟合值的相关性在0.9997～1.0000,相关性接近1,测量值与拟合值数值接近,模型效果较好;由表8可知,五个温度梯度下样品的羰基价的测量值与拟合值的相关性在均为1.0000,且测量值与拟合值数值接近,模型效果较好;由表9可知,五个温度梯度下样品的极性组分的测量值与拟合值的相关性在0.9995～0.9999,相关性接近1,测量值与拟合值数值接近,模型效果较好。因此三个理化指标模型均能较准确地预测煎炸油实时酸价、羰基价、极性组分情况。

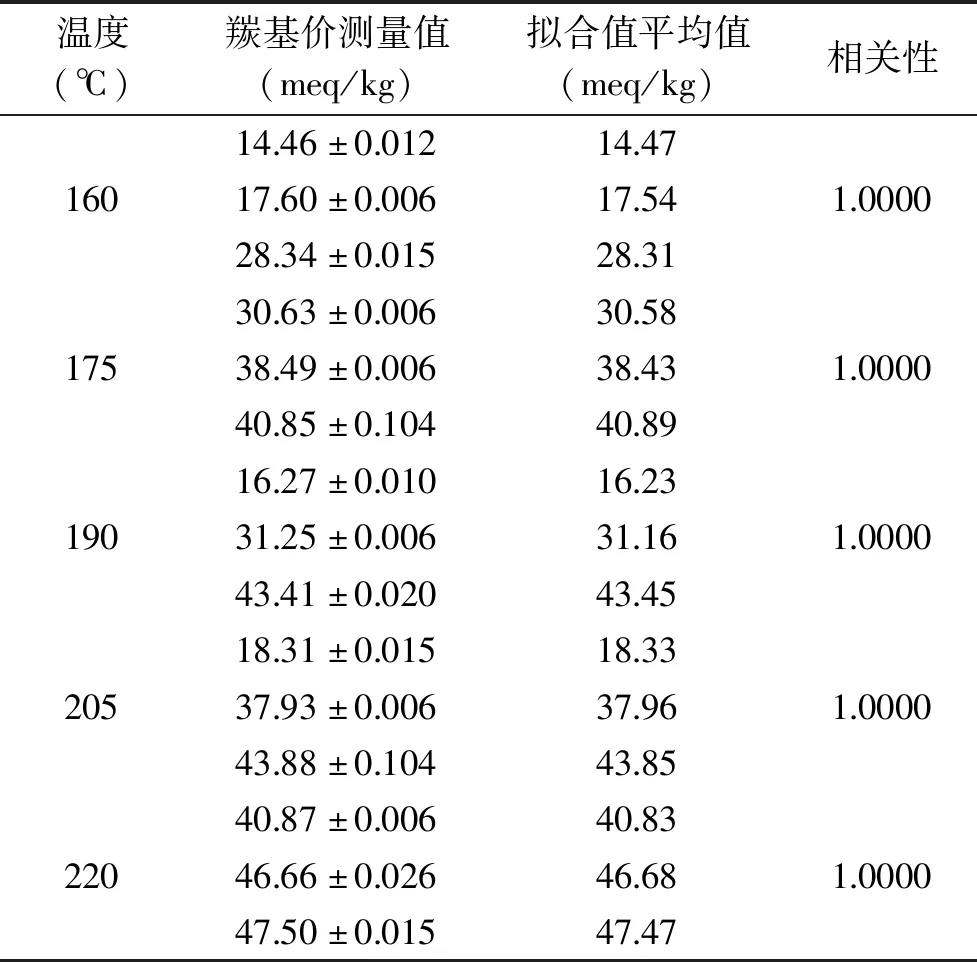
表8 各温度梯度羰基价的模型验证Table 8 Model verification of carbonyl value of each temperature gradient

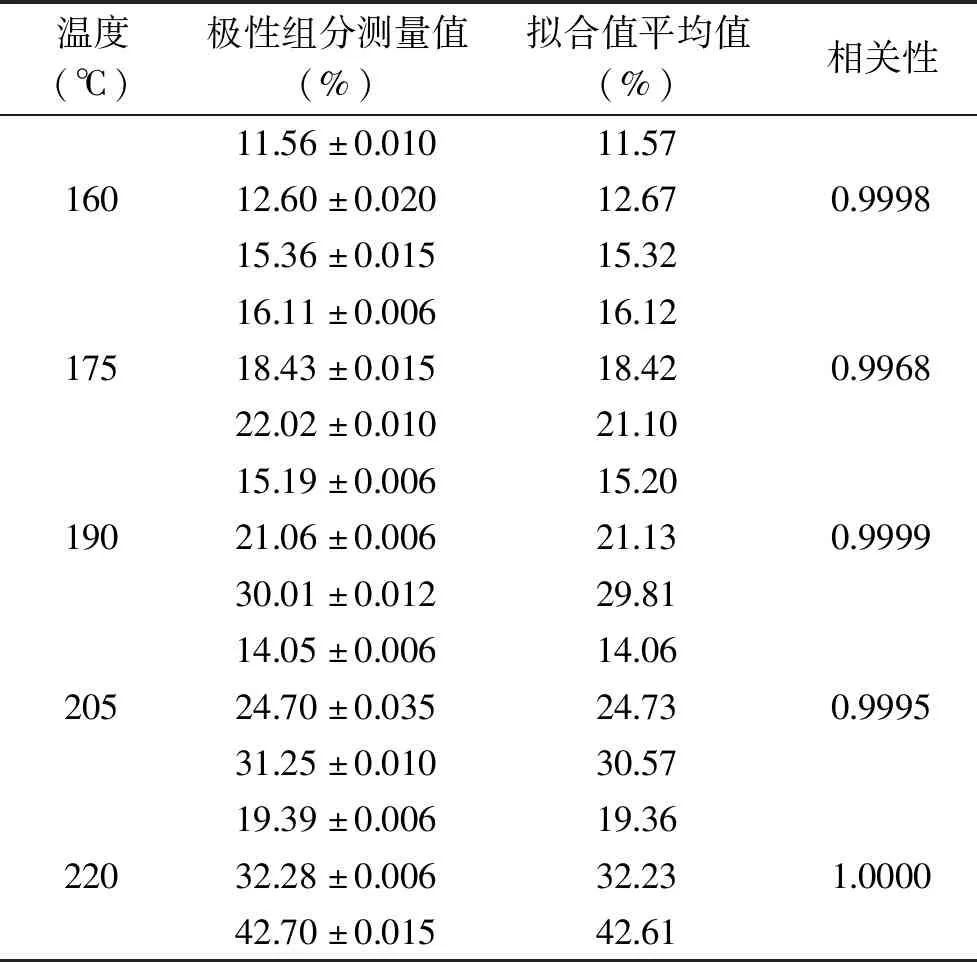
表9 各温度梯度极性组分的模型验证Table 9 Model verification of polar components of each temperature gradient

3 结论

通过进行多项式拟合建模,再通过删除学生化残差绝对值>3、Cook距离>1找到异常值,再通过Matlab剔除异常值后进行拟合和作图后,得到的R2均接近1,拟合效果较好,模型较成功。除此之外,模型可以较为准确地预测某一特定时间的油脂实时质量情况,只要给出一个特定的时间,Matlab便会按照模型快速给出三个理化指标的实时数值,相关性在0.99以上,结果可以与国标规定的煎炸油的废弃点进行对比,从而判断油脂的质量情况。