放射源跌落冲击响应谱仿真与分析

武伟名，牛厂磊，李 鑫，唐 显

(中国原子能科学研究院 同位素研究所，北京 102413)

放射源是由放射性同位素物质制成的辐射源，通常由外层金属包壳和内部放射性同位素源芯两部分构成，外层的金属包壳起到保护放射性物质不发生泄露的作用。在储存、运输、使用过程中，放射源产品可能要经受冲击、撞击、穿刺等各种工况条件，因此要严格保证放射源的安全性和可靠性，避免因放射性物质泄露造成巨大危害。在放射源可能经受的安全性事故工况中，跌落冲击是放射源使用中最可能发生的，国家标准《GB 11806-2004放射性物质安全运输规程》中明确规定了特殊形式放射源试样及货包的跌落冲击试验要求，因此，研究放射源跌落冲击对放射源结构设计具有一定的指导意义。

冲击响应谱在结构设计与分析方面的用途主要是用来衡量冲击的作用和效果，从而评估冲击对结构的损伤势[3-4]，根据冲击响应谱，可以评估在冲击作用下结构零件的强度和安全性。雷晓波等[5]通过分析飞机着陆的冲击响应谱，评估了机载设备的抗冲击特性以及减震防冲设计；王珂等[6]计算了水下爆炸冲击作用下舰船各测点的加速度冲击响应谱，分析不同爆炸冲击工况时的舰船及舰载设备冲击环境。高山等[7]根据陆军惯性导航设备的冲击载荷计算了相应的冲击谱，基于谱分析法计算机箱对冲击谱的响应分析，分析结果为机箱的抗冲击优化设计提供指导。根据放射源跌落冲击响应谱可以确定放射源在跌落冲击环境下的系统最大响应，分析不同跌落试验条件下放射源结构共振产生冲击损伤，为放射源的结构设计及优化提供依据。

本研究拟通过典型锶-90密封放射源跌落冲击过程的有限元模拟，得到冲击载荷作用下测点加速度时域响应数据；基于改进的递归数字滤波法和加速度时域数据，通过自编的Matlab计算程序，得到相应的放射源跌落冲击响应谱，并在此基础上得到不同条件下的放射源跌落冲击响应谱。

1 冲击响应谱

1.1 冲击响应谱概念与模型

冲击响应谱通常又称“冲击谱”[8-9]，是指一系列单自由度质量阻尼系统，在冲击激励函数作用下，各单自由度系统产生的响应峰值作为单自由度系统固有频率的函数绘制的曲线。即在笛卡尔坐标系下以单自由度系统的固有频率为横坐标，以其响应峰值为纵坐标绘制的曲线。通过冲击响应谱的分析，对设备各部件所承受的最大动力载荷准确把握，从而预测冲击潜在的破坏。

一个实际的物理系统可以分解为多个不同的单自由度系统，对每个单自由度系统进行冲击响应分析计算，取系统响应的最大值，然后和它的固有频率组成一个数据点。这样分解成多少个单自由度系统就可以得到多少组数据点。最后将这些点加以合成，即可得整个系统的冲击响应谱，原理示于图1。

图1 冲击响应谱定义物理模型Fig.1 Physical model of shock response spectrum

冲击响应谱根据相应峰值取法的不同分为最大响应谱、初始响应谱和剩余响应谱。初始响应谱指冲击作用时间内的相应峰值求得的冲击响应谱；剩余响应谱指冲击激励结束后的相应峰值做出的冲击响应谱。

冲击响应可用加速度、速度、位移和应力来描述，按工程需要冲击响应谱通常表示为加速度响应谱、速度响应谱和位移响应谱3种冲击响应谱。在工程上，一般采用最大绝对加速度谱和最大相对位移谱，前者多用于规范冲击环境，后者多用于考核冲击强度及设计减震装置。

1.2 冲击响应谱的计算方法

图2 单自由度系统模型Fig.2 Single degree of freedom system

根据冲击响应谱的定义求解冲击响应谱，单自由度振动系统的模型如图2所示，当基础受到外界激励时，质量为m的振子动力学运动方程为：

单自由度谐振子的振动方程为：

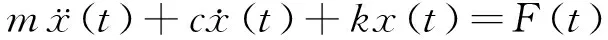
(1)

其中m、c、k分别为系统的质量、阻尼和刚度；

(2)

式中fn和ξ分别表示系统的固有频率和阻尼比。

方程(2)的通解为：

(3)

冲击响应谱的数值解法较多[10-12]，主要有直接积分法、FFT变换法、递推法和递归数字滤波法。目前最成熟和普遍应用的冲击响应谱计算方法是由Smallwood提出改进的递归数字滤波法[13]，该方法舍弃了常用的激冲不变的滤波器模型，设计了一种新的斜坡不变模型，其计算过程如下：

设单自由度系统基础和加速度的输入U(t)的采样值为Uk，k=0,1…，则有：

Xk=b0Uk+b1Uk-1+b2Uk-2+

q1Xk-1+q2Xk-2k≥2

(4)

式中：

q1=2e-DcosE

q2=-e-2D

D=ζωΔt

E=ωdΔt

ω=2πf

其中，f是系统频率，Δt为采样频率，ζ为系统阻尼系数。

2 跌落有限元模型及材料参数

2.1 放射源结构及材料参数

以锶-90同位素密封性放射源为例分析放射源跌落冲击环境。如图3所示，锶-90同位素放射源采用典型的柱状密封放射源结构，源芯尺寸为25.5 mm×25.5 mm，整个放射源高38 mm，直径32 mm。采用双层镍基718合金包壳密封，源芯形式为钛酸锶烧结陶瓷，垫片材料与包壳相同，跌落目标靶选择混凝土材料。各材料在室温环境的参数见表1[14-15]。

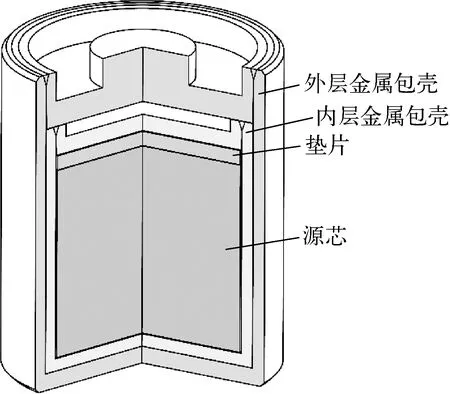
图3 锶-90放射源结构示意图Fig.3 Strontium-90 radioactive source structure diagram

表1 材料参数Table 1 Material parameters

2.2 跌落有限元模型

对放射源划分有限元网格，放射源各部件均采用六面体单元划分；材料模型均采用各向同性强化弹塑性模型。自由跌落模拟分析中，选择三种典型的跌落姿态：竖直跌落、倾斜跌落和侧面跌落，倾斜跌落时放射源的中轴线与靶面的夹角为49.5°(放射源重力线通过跌落点)，如图4所示为放射源跌落有限元网格和跌落姿态示意图。

图4 有限元网格及典型跌落姿态示意图Fig.4 Finite element mesh and typical drop attitude diagram

3 冲击响应谱仿真与分析

应用Ansys-Autodyn软件仿真模拟放射源自由跌落冲击混凝土表面，通过在包壳撞击位置设置监测点，得到放射源包壳跌落冲击加速度时域脉冲信号，加速度信号采样频率为6×107Hz。采用改进的递归数字滤波法，通过Matlab软件编写冲击响应谱计算程序，计算得各测点的跌落冲击响应谱，冲击响应谱的计算频率范围为10～107Hz，1/12倍频程，阻尼系数ζ=0.05。

3.1 不同位置测点的冲击响应谱分析

模拟放射源1 m竖直自由跌落，如图5所示。沿冲击波传递方向，分别在每层包壳的圆柱底面、侧面以及顶端中心位置设置监测点，得到包壳在测点位置的加速度脉冲信号，计算响应的冲击响应谱，分析放射源跌时落冲击对不同区域的影响。

图5 不同位置测点分布Fig.5 Distribution of measuring points at different positions

图6所示为包壳1 m高度自由跌落的加速度信号及冲击响应谱。可以看出，放射源的跌落冲击环境为典型的振荡型冲击环境，并且冲击作用持续时间极短(小于0.2 ms)；由于放射源模型为装配体，冲击载荷作用结束后，冲击波在包壳之间传递，使得测点加速度响应持续时间远大于冲击作用时间。

从跌落加速度冲击响应谱可以看出，放射源跌落冲击响应随着分析频率增大逐渐上升，直到105～106Hz频率段出现上升拐点，说明跌落冲击脉冲主要为高频信号；从各个测点的加速度冲击响应谱可以看出，在低频区域，每个位置的冲击响应谱平稳上升且谱值基本相等，当频率大于1 000 Hz以后，各个测点的加速度谱值逐渐区分开，内层包壳和外层包壳底部接近撞击位置测点的加速度响应明显高于其他位置。此外，外层包壳和内层包壳冲击响应谱值大小基本相当，说明内外两层包壳所承受的跌落冲击环境相同。

从图7所示的冲击响应谱可以看到，在高频区域各测点的加速度谱值出现了一些大的响应峰值，说明射源包壳或部件的自振频率落在该频率区域，引起结构的共振，放大跌落冲击的损伤势。在设计放射源结构时，可以通过优化设计(包壳尺寸、厚度以及材料等)消除或降低结构共振的影响，从而达到提高放射源结构抗冲击性的目的。

3.2 不同跌落姿态冲击响应谱分析

对锶-90放射源1 m跌落，以三种典型姿态跌落冲击进行计算，冲击响应谱分析对应的模型测点位置为外层包壳撞击位置的几何中心，对比不同姿态跌落加速器冲击响应谱，如图8所示。

在中低频段(<103Hz)冲击谱呈上升趋势，并且三种姿态的谱值和上升斜率基本相同，由于放射源各部件的自振频率均大于103Hz，因此冲击响应谱值随着频率增大平稳上升，未出现结构共振引起的峰值响应。

图6 各测点的加速度脉冲信号Fig.6 Acceleration pulse signal of measure point

a——外层包壳测点；b——内层包壳测点图7 包壳测点最大加速度冲击响应谱a——Gauges of outer cladding；b——Gauges of inner claddingFig.7 Maximum acceleration SPS at measuring points of cladding

在高频段(103～107)，冲击响应谱出现大小不同的响应峰值，可以看到，不同姿态冲击的响应峰值的分布基本相同；在2×106Hz时，倾斜跌落和侧面跌落的响应峰值明显弱于竖直跌落，说明冲击方向的改变使得结构固有频率在2×106Hz的响应峰值显著降低。

由于撞击产生的冲击加速度信号为高频信号，三种姿态跌落产生的信号峰值和持续时间的差异使得冲击响应谱值大小明显不同。从冲击谱的冲击量级可以看出，竖直跌落和侧面跌落的冲击量级高于倾斜跌落，这主要是由于倾斜跌落时包壳与混凝土表面接触面积小，碰撞位置包壳产生局部塑形吸能和缓冲。

图8 放射源1 m自由跌落加速度冲击响应谱Fig.8 Shock response spectrum of 1 m free drop acceleration

3.3 不同跌落高度冲击响应谱分析

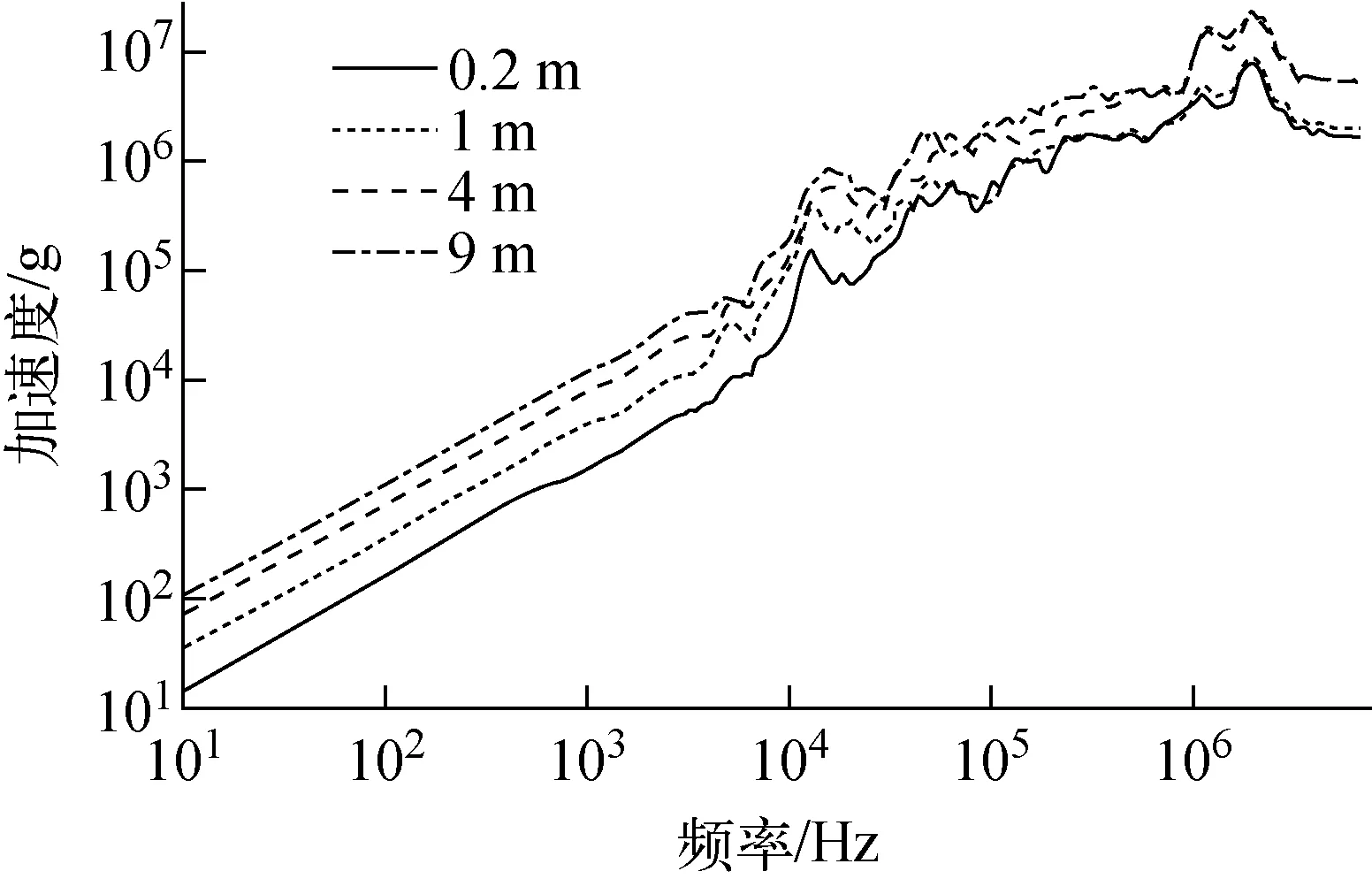
图9 不同高度跌落的冲击响应谱(竖直跌落)Fig.9 Shock response spectra of drops at different heights (vertical drop)

实际放射源跌落时，可能会以不同的高度跌落，分析和对比锶-90放射源以不同高度跌落冲击的冲击响应谱。采用竖直跌落姿态，加速度信号测点位置选择图5所示A点，计算结果如图9所示。

由图9可知，随着高度的增加，加速度谱值也增大，并且冲击响应谱的斜率和拐点频率均不发生变化。在高频段，受放射源结构共振放大效应的影响，不同高度的冲击响应谱出现交叉与重叠，可以看到，由于共振的放大作用，在固有频率为105～106Hz时，4 m和9 m跌落的冲击损伤势基本相当。

图10所示为线性坐标系下放射源跌落冲击响应加速度谱值随跌落高度变化，选择分析频率为1 300 Hz，可以看到，跌落加速度谱值随着跌落高度增加呈对数增长规律。

图10 加速度谱值随跌落高度变化(频率1 300 Hz)Fig.10 Acceleration spectrum varies with drop height at 1 300 Hz

4 结论

采用有限元方法对典型圆柱体锶-90放射源跌落冲击进行仿真计算，基于改进的递归数字滤波法和加速度时域数据，通过Matlab编写计算程序，得到相应的放射源跌落冲击响应谱，分析并总结放射源跌落冲击环境特点及规律，得出如下结论。

1) 放射源的跌落冲击环境为振荡型冲击环境，跌落冲击脉冲主要为高频信号。

2) 相同的高度跌落，若放射源的冲击姿态不同，其冲击响应谱值也存一定差异：在中低频段(<103Hz)，由于冲击作用的影响小，不同跌落姿态跌落冲击损伤势基本相同；在高频段(103～107)，不同姿态跌落产生的信号峰值和持续时间的差异使得冲击响应谱值大小明显不同，倾斜跌落损伤势低于竖直跌落和侧面跌落。

3) 随着高度的增加，加速度谱值也增大，放射源跌落加速度冲击损伤势随着跌落高度增加呈对数增长规律。

4) 通过放射源的跌落冲击响应谱能够确定跌落冲击中结构产生共振响应，若放射源跌落冲击响应谱出现明显的共振响应峰值(通过放大倍数判断)，应采取抗冲击设计(优化包壳尺寸、厚度以及材料等)，以消除或降低结构共振的影响。