基于Abaqus的放射性光源激光封割技术仿真研究

李思杰，马俊平，平杰红，唐 显，孙玉华

(中国原子能科学研究院，北京 102413)

放射性光源是将放射性气体密封在涂有荧光层的玻璃管内，通过放射性气体(通常为气态氚)衰变发出的β粒子激发荧光物质原子而发光，具有使用寿命长、光强稳定、无需电源、无需维护等优点[1-4]。其制备流程主要包括玻璃成型、荧光粉涂覆、填充放射性物质及封割四个步骤。其中，封割是指将内充有放射性气体的密封长玻璃管分割成合适长度的放射性光源，在分割的同时需对端口进行密封，以防止放射性气体泄漏，因此，封割是关键步骤之一，封割效果决定放射性光源的成品与质量。传统的放射性光源采用火焰封割，此方法依赖操作人员的经验与熟练程度，放射性光源成品的美观性和成品率都难以得到保证。和传统的火焰封割方法相比，激光技术更适用于放射性光源的封割，其能量密度大，热影响区域小，封割速度快，且更精确可控、安全。对放射性光源封割而言，通常采用的是CO2激光，波长为10.6 μm，比较容易被玻璃吸收，更适用于玻璃材料的加工处理[5-6]。

激光封割放射性光源是利用激光的高能量密度加热放射性光源玻璃管，在相应的激光功率密度下，激光束的能量被玻璃管吸收，引起激光作用点的温度急剧上升，达到熔融点后，玻璃管封割点开始软化，随着激光束和玻璃管的相对运动，在离心力、内外压差和热应力等多因素共同作用下，完成对玻璃管的封割。在进行封割技术研究时，为减少实验次数和放射性废物的产生，利用有限元方法进行仿真，以理论指导实验；而Abaqus是一种功能强大的基于有限元方法的工程模拟软件，它不仅能解决结构分析(应力/位移)问题，还能模拟和研究热传导、质量扩散等广阔领域的问题[7-8]。本研究借助有限元分析软件Abaqus，建立放射性光源激光封割的仿真模型，分析激光对放射性光源玻璃管的影响，拟为最终确立放射性光源激光封割的条件参数提供指导。

1 仿真模型

应用Abaqus有限元分析软件对放射性光源激光封割进行仿真分析。首先建立仿真模拟的几何模型，然后建立传热-应力分析物理模型，提交任务进行计算，最后对计算结果进行处理。

激光封割放射性光源的运动示意图示于图1。放射性光源玻璃管以一定速度旋转，一束激光辐照到玻璃管上，玻璃管温度上升，激光束位置的玻璃熔融，激光束停止辐照，实现放射性光源玻璃管分开并密封。

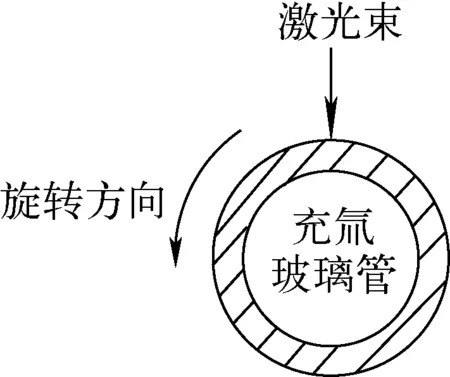
图1 激光封割放射性光源运动示意图Fig.1 Schematic diagram of laser sealing and cutting tritium light source

玻璃管外径为1.5 mm，壁厚为0.25 mm，建立如图2的计算模型及网格，激光作用区域及其附近有限元单元网格划分较密，而其余区域网络相对稀疏，单元类型为C3D8T。

图2 仿真用几何模型及其网络Fig.2 Geometric model and its grid for simulation

激光辐照到旋转的玻璃管上，其温度场为无内热源的非线性瞬态热传导方程[9]，表示为：

(1)

式中，T为材料结构温度，K；t为时间，s；c为材料的定容比热，J/(kg·K)；ρ为材料的密度，kg/m3；λ为导热系数，W/(m·K)；r、θ、z为极坐标的三个坐标变量。

由于温度迅速变化和温差较大导致的热膨胀情况不一致，因此，在激光封割过程中，放射性光源玻璃管材料内部产生较大的应力，即热应力。热应力与温度和材料的膨胀系数关系为[10]：

αT(T0)(T0-Tref)

(2)

式中，αT为热膨胀系数，1/K；Tref为参考温度，K；T0为初始温度，K。激光直接作用于表面薄层，对其进行加热，然后再通过热传导间接作用于材料内部，因此，在应用Abaqus对激光辐照下放射性光源玻璃管的温度和应力分布进行模拟时，激光热源为高斯分布，并随着进入材料的深度而线性减小，其分布为[3]：

(3)

式中，QL为激光功率，W；r0为束斑半径，mm；d为激光热源作用深度，mm；r为瞬态激光束位置，其中，r与x、y、z关系为：

r2=x2+y2+z2

(4)

x、y、z为t时刻激光束坐标。在封割的过程中，激光热源固定，玻璃管转动；但在进行仿真模拟时，由于是分析温度场变化及相应的应力分布情况，因此不能直接施加玻璃管转动作为边界条件，为了模拟实际状态，在Abaqus中将激光热源作绕圆周运动，实现等效封割条件。

激光在沿圆柱面辐照的过程中，激光热源作为函数型热通量进行加载，该热通量通过用户子程序施加到圆周上，公式(1)～(4)构成了求解激光热传导方程组。在用户子程序中，束斑直径设置为1.5 mm，转速为300 r/min，玻璃管壁厚即为激光热源的渗透深度。

由于激光照射加热时间极短，模型中热边界条件并未考虑对流和辐射传热的影响，放射性光源所用玻璃载体的泊松比为0.2，相关热导率随着温度变化的相关参数设定列于表1。

表1 热导率参数设定Table 1 Thermal conductivity parameter setting

2 仿真结果与讨论

运用已建立的仿真模型，得到激光封割的仿真结果。激光功率为10 W时，放射性光源玻璃管上设置固定监测点的温度场在玻璃管径向上随着时间的变化趋势示于图3。从图3结果可以看出，监测点的温度随着封割时间的增加而规律性地迅速升高，直至达到玻璃管的熔融温度，当t=1.15 s时，温度达到了约1 500 K(该温度适于放射性光源玻璃管的封割)。

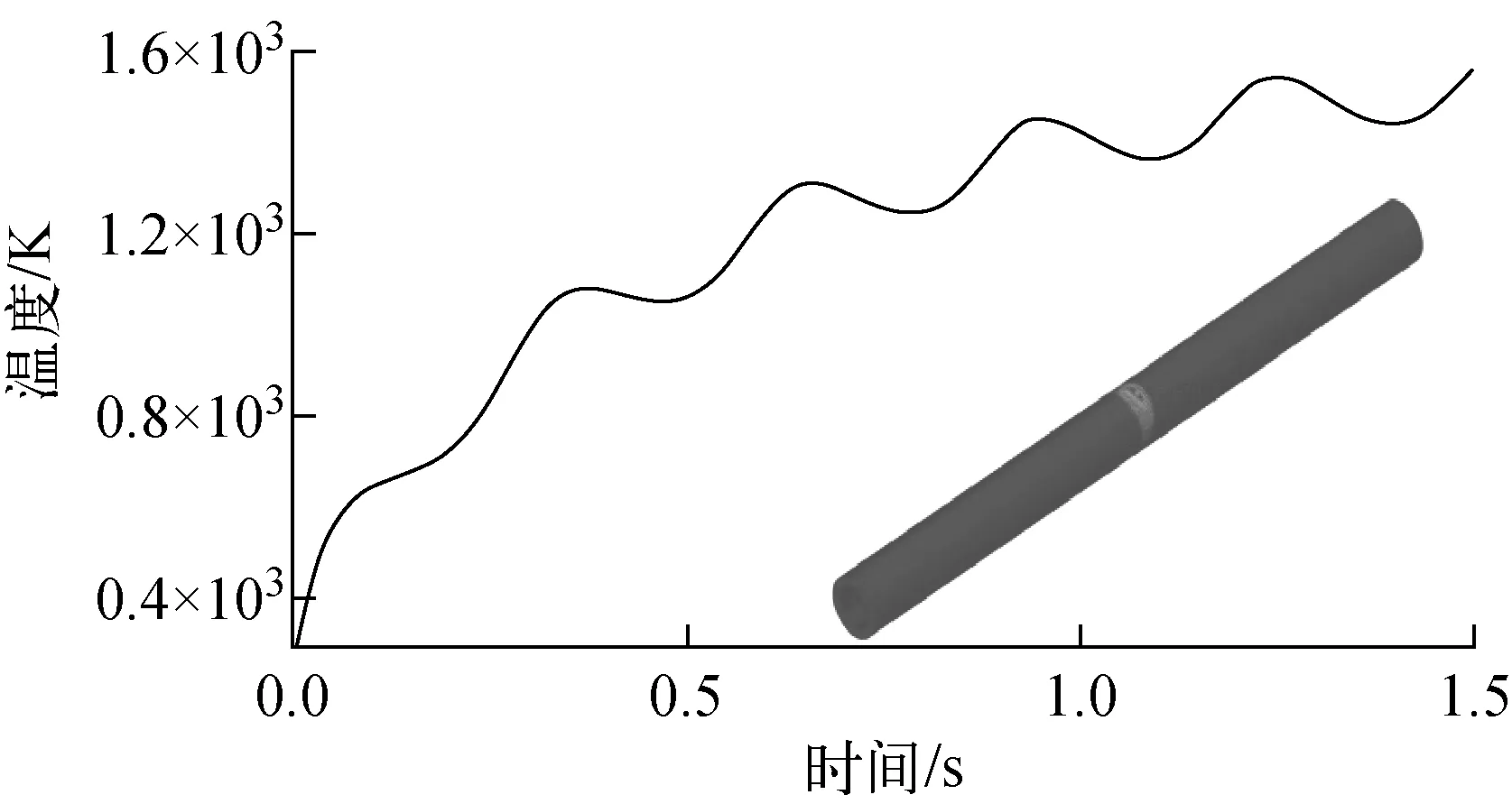
图3 监测点温度随着时间变化Fig.3 Temperature Vs. time of the monitoring point

在t=1.15 s时刻玻璃管的轴向温度云图分布结果示于图4。从图4结果可以看出，激光中心温度最高，然后沿轴向两侧迅速下降，呈高斯分布；光斑中心所在的整个圆周上，温度明显高于周围区域，因此，激光辐照在放射性光源玻璃管圆周上，可以实现整管同时熔融。

图4 t=1.15 s时刻的轴向温度场分布Fig.4 Axial temperature field distribution at time t=1.15 s

由于封割过程中激光能量高度集中，在玻璃管上的能量沉积亦是高度集中，因此在放射性光源玻璃管上会出现较大的温度差异，造成热冲击，导致玻璃材料内部出现较大的热应力。监测点应力随着封割时间的变化趋势示于图5。由图5结果可知，在t=0.03 s时便出现了最大的应力，且在此过程中可以看到，随着激光辐照时间增加，由于热传递的作用，中心区域温差变小，应力逐渐向圆周两侧移动，但整个过程中最大热应力均小于放射性光源玻璃的破坏应力90～110 MPa，因此，激光封割过程中玻璃管不会出现炸裂的情况。

分别对在放射性光源封割过程中的不同激光功率进行仿真分析，得到达到封割温度时所需的最短时间及其温度场分布，结果示于图6。从图6结果可以看出，随着激光功率增大，封割放射性光源玻璃管所需的时间减小，当激光功率达到20 W以后，达到满足封割条件所需的时间差别较小，说明此时为高斯分布的激光热源，进入材料的渗透分布深度已接近放射性光源玻璃管的壁厚。

图5 监测点应力随时间变化Fig.5 Stressat the monitoring point Vs. Time

图6 不同激光功率下的封割时间及其温度场分布Fig.6 Sealing time and temperature distribution with different laser powers

3 实验验证

利用现有的激光封割系统，对仿真结果进行验证，结果示于图7。由图7结果可以看出，仿真值与实验值变化趋势相同，在某个激光功率条件下，激光辐照封割时间计算值比实验值略短,这是由于在仿真模拟激光封割的计算模型中，忽略了激光传输过程引起的气体热效应、周围环境对流散热以及放射性光源玻璃管的辐射散热等因素。总体来说，仿真结果能较真实地反映激光封割放射性光源玻璃管的情况。

图7 激光功率与激光辐照封割时间关系Fig.7 Laser power and Vs. sealing time

4 结论

本文利用有限元软件Abaqus，对放射性光源的激光封割技术进行仿真，得到了旋转的放射性光源玻璃管在激光辐照下随着时间变化的温度分布及热应力分布，以及不同激光功率与封割时间的关系，随着激光功率增大，所需的封割时间越小，最后通过实验验证，得到封割的仿真值与实验值较为一致。本文的模拟结果和分析首次为放射性光源研制的激光封割技术提供了理论指导和实验验证，可为最终确立放射性光源研制的重要关键技术参数提供参考。