基于梯度上升算法的丢失放射源搜寻方法

2021-12-31孟令飞杨飞莹田浩浩

核安全 2021年6期

孟令飞，刘沧，杨飞莹，傅燕，田浩浩

（中陕核工业集团综合分析测试有限公司，西安 710024）

随着核科学与技术的发展，放射源在工业、医学、农业、科研等领域得到了广泛应用，如辐照灭菌、工业探伤、含密封源测井、辐射诱变育种、放射诊疗、放射性测井等。放射源的广泛应用在促进社会和经济发展的同时，也存在着辐射安全隐患。诸如放射源丢失、被盗、失控辐射事故等，会危害环境和公众健康。由于苏联切尔诺贝利核事故和日本福岛核事故的影响，社会公众往往“谈核色变”。因此，一旦发生放射源丢失事故，快速定位放射源对减少公众和环境危害，消除社会恐慌具有重要意义。对丢失放射源的搜寻工作通常建立在放射源失去屏蔽或部分失去屏蔽的基础上。对于完全屏蔽的放射源，主要通过电离辐射标志、屏蔽容器外形等特征进行目视搜寻，辐射探测为辅助手段。

近年来，国内外对丢失放射源搜寻均开展了诸多研究。其中，IAEA在《废放射源的鉴别和定位方法》（IAEA-TECDOC-804）中给出了废放射源的野外搜寻方法［1］，在《核或辐射应急时通用监测程序》（IAEA-TECDOC-1092）中给出了估算放射源距离的方法［2］。刘新华等提出采用平行线法搜寻丢失放射源［3］。黄超云等探讨了孤儿源的搜寻方法［4］。李远辉等提出采用预估带法搜寻丢失放射源［5］。左国平等提出基于三角圆筒铅屏蔽探测器进行放射源定位［6］。

1 平行线搜寻法

IAEA技术文件《废放射源的鉴别和定位方法》（IAEA-TECDOC-804）中给出了一种放射源定位方法，如图1所示。

图1 平行线搜寻法示例图Fig.1 Example diagram of parallel line search method

平行线搜寻法的优点是能够不遗漏地搜寻整个区域，缺点是需要探测的点较多，不能快速定位放射源，因此需要对此方法加以改进。

2 辐射场分布

2.1 天然本底辐射场

构想一个100 m×100 m的平面区域，在无放射源时，该区域辐射贡献为天然本底辐射，西安市2021年8月环境γ辐射剂量率范围为0.090~0.121μGy/h，以此剂量率范围构建该区域地面1 m高度处的辐射场分布，如图2所示。

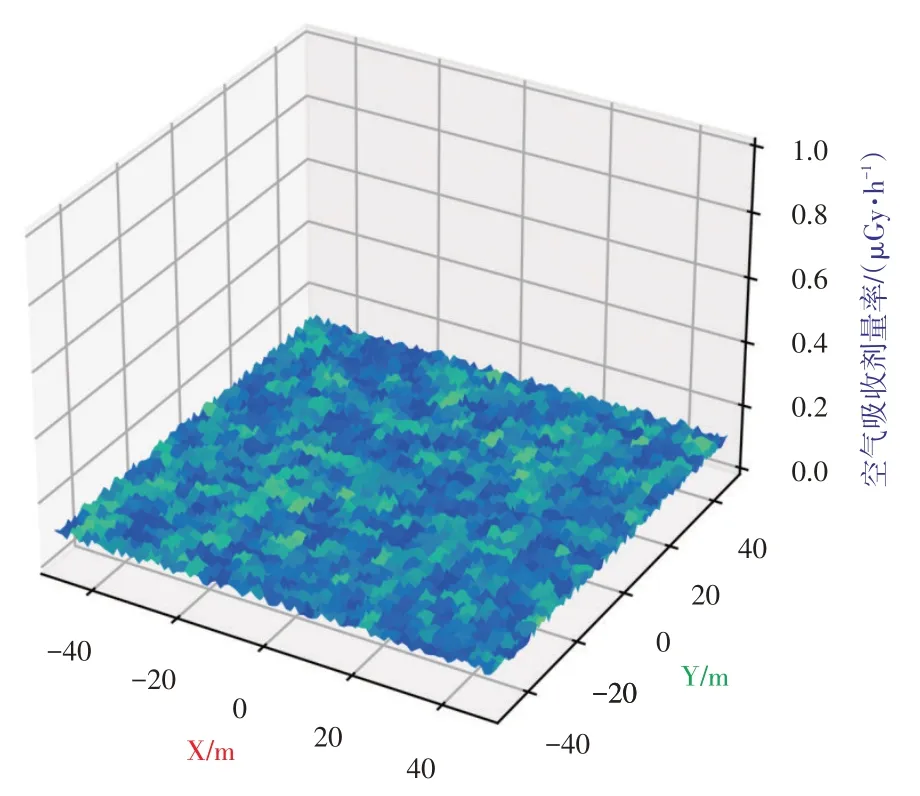
图2 本底辐射场示意图Fig.2 Diagram of background radiation field

2.2 放射源辐射场

在该区域某一位置放置一无屏蔽放射源，该辐射源会显著影响该区域的辐射场分布。假设放射源为Ⅴ类Cs-137放射源，活度为2.59×108Bq。对于点源，辐射场按式（1）分布。

A：放射源活度，Bq；

Γ：空气比释动能率常数，Cs-137取2.12×10-17Gy·m2·Bq-1·s-1；

r：关注点与放射源距离。

设放射源所在点坐标为（x0，y0），搜寻点为（x，y），根据式（1），得出式（2）。

将放射源所致空气比释动能率与图2的本底辐射场叠加，如图3所示。

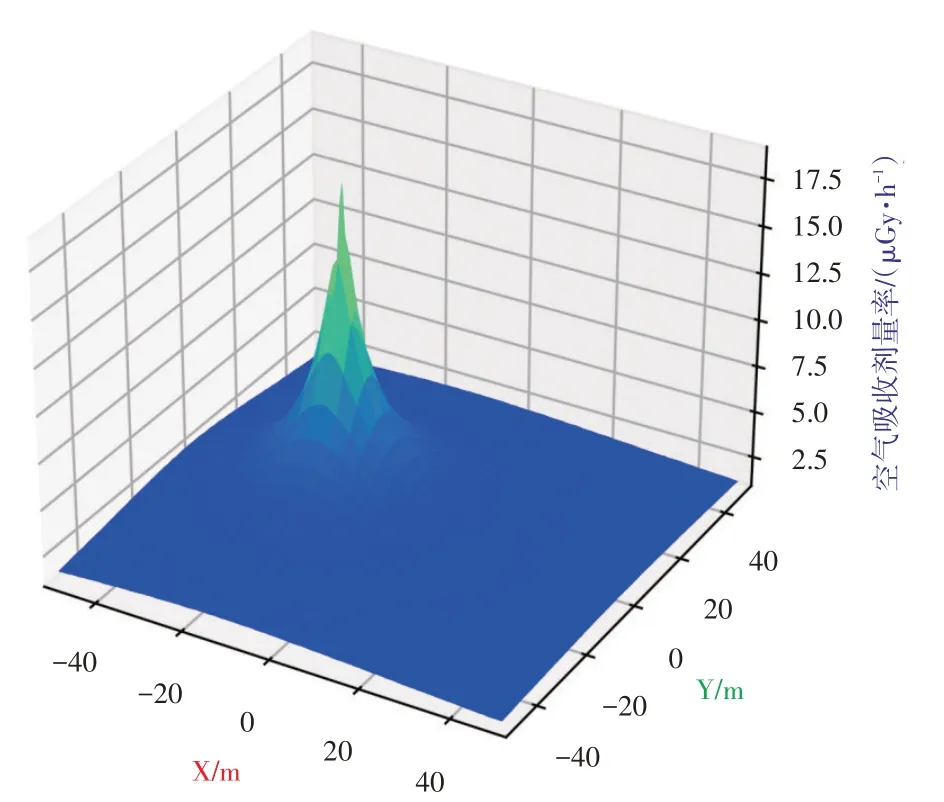
图3 放射源辐射场示意图Fig.3 Diagram of radiation field of radioactive source

3 梯度上升算法搜寻放射源

3.1 基本步骤

在图3的辐射场中，剂量率分布如式（2），该二元函数具有一阶连续偏导数，对于该函数上任一点P（x，y），均可计算该点处的梯度∇f（x，y），计算方法如式（3）。

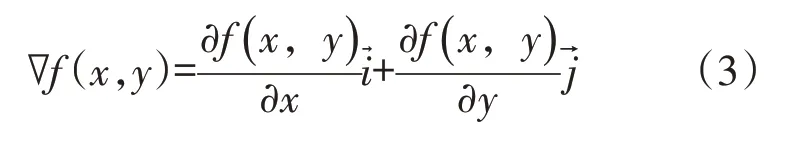
根据式（3），剂量率（x，y）的梯度函数为：

在测得（x，y）的点剂量率后，根据式（4），在X方向步进一小段距离Δx，测得（x+Δx，y）的点剂量率，可得到X方向的梯度向量；同理，根据式（5），可得到Y方向的梯度向量。梯度向量总是指向函数值增大的方向，因此可利用梯度方向寻找放射源。使用梯度上升算法搜寻放射源的步骤如下。

（1）在拟搜寻区域附近获取环境本底值；

（2）选定拟搜寻区域的一条边界作为初始搜寻方向；

（3）选择适宜的步进距离间隔搜寻，按照平行线搜寻法搜寻放射源，直到发现剂量率达到本底值3倍的点，将该点作为使用梯度搜寻算法搜寻放射源的初始点位；

（4）按照式（4）和式（5），选择适当的试探搜寻距离Δx和Δy，并计算梯度向量；

（5）选择适当的步进距离沿梯度方向步进到新点；

（6）重复步骤（4）和（5）；

（7）当发现放射源或剂量率水平接近100 mSv/h时停止搜寻。剂量率水平接近100 mSv/h时，通过监测和计算确定放射源的具体方位和距离。

在初期搜寻时，使用探测下限低的环境级监测仪表可以更灵敏地发现剂量率变化。当剂量率监测结果接近环境级监测仪器的量程上限时，需替换为高量程的防护级监测仪表。

3.2 试探搜寻距离设置

试探搜寻距离Δx=Δy，具体距离应使剂量率发生显著变化，变化量应超过监测设备的探测下限。

3.3 初始步进距离设定

一般认为达到3倍天然本底辐射的剂量率即视为存在放射源的辐射场影响，以2.1中的天然本底辐射水平和2.2中的放射源为例，设距放射源r米处可发现放射源，根据式（1）可得：

解得：r=7.4 m

对于完全裸露的Ⅱ类放射源，在距源数百米处即可被发现。对于完全裸露的最低活度V类放射源，在距源1 m范围内，也很难被发现。在发生放射源丢失辐射事故后，一般能通过《辐射安全许可证》等资料获得放射源的基本信息，由此可推算出初始步进距离。考虑到放射源可能仍处于屏蔽状态，则初始步进距离不宜过长，需视现场环境综合考虑目视搜寻的适宜距离。

3.4 步进距离调整

如果每次的步进距离固定，在放射源位置附近，会发生无意义的往复迭代。越接近放射源，需要步进的距离就越短，根据式（1），设定步进的调整方法如下：

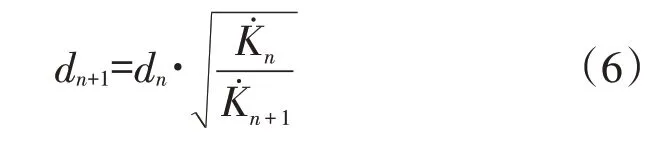
式中，dn+1：第n+1次步进距离，m；

dn：第n次步进距离，d0为初始步进，m；

：第n+1次测量剂量率，Gy·h-1。

4 编程验证

使用Python语言编写程序构造若干辐射场（如图4所示），并模拟上述梯度上升算法搜寻放射源，其中搜寻放射源的部分代码如下。

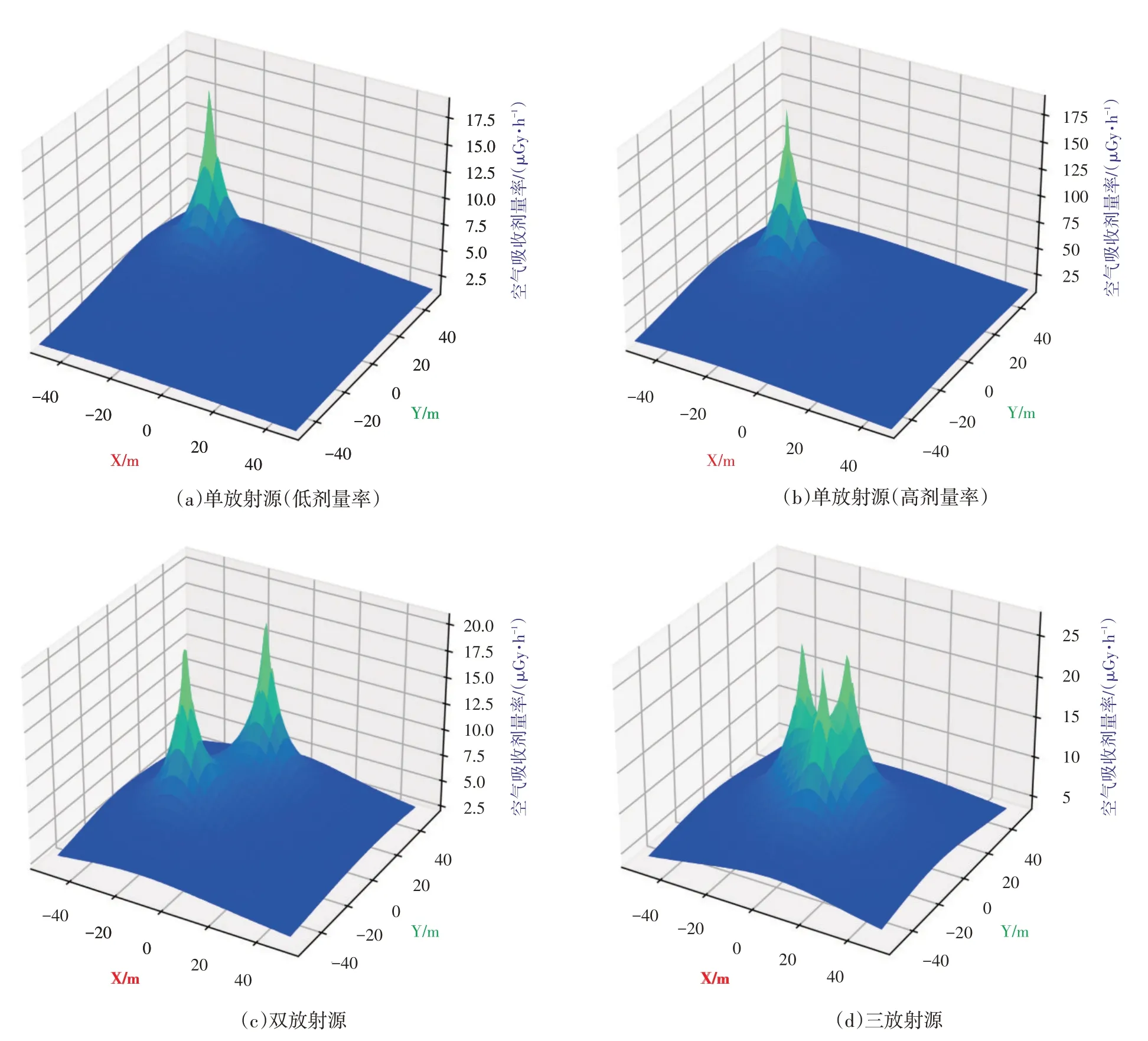
图4 构造辐射场示意图Fig.4 Diagram of constructing radiation field

while True:

print（“z［x0］［y0］=”，z［x0］［y0］）

if z［x0］［y0］>10:

print（“search over”）

print（“x0=”，x0）

print（“y0=”，y0）

break

i=z［x0+1］［y0］-z［x0］［y0］

j=z［x0］［y0+1］-z［x0］［y0］

ifi>0:

x0=x0+d

else:

x0=x0-d

if j>0:

y0=y0+d

else:

y0=y0-d

图4中（a）和（b）为单个放射源，（b）的放射源活度为（a）的10倍；（a）、（c）、（d）所用放射源活度一致，（a）为单放射源，（c）为双放射源，（d）为三放射源。经验证，图4中所构造的四个辐射场中，梯度上升算法均能搜寻到放射源。作为对比，同为单放射源，活度更高的所需搜寻次数更少；相同活度放射源，放射源数量越多，所需搜寻次数越少。