一道立几高考试题的解法研究

李高磊

摘 要：历年高考中，立体几何及其相关的证明问题都是数学科目的重点中的重点，除证明面与线，线与线，面与面的平行和垂直之外，二面角角度的求法也是历年来高考数学立体几何大题的“标配”。很多学生在证明面线、面面和线线的平行与垂直方面掌握得较为完备，但是却在求二面角的问题上栽了跟头，因此，笔者认为应该着重研究如何求立体几何证明大题中的二面角问题，以保证学生们能够在立体几何的高考题目上拿到满分。

关键词：立体几何；高考题目；解法研究

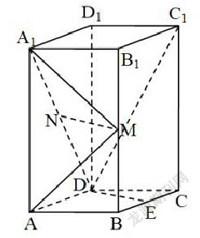
题目：如下图，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E、M、N分别是BC、BB1和A1D的中点。

（1）证明：MN∥平面C1DE；

（2）求二面角A-MA1-N的正弦值。

思考与解答过程：对于第一小题来说，最为关键的是要能够寻找或者说是构建出一个能够经过MN且和平面C1DE相交的平面，而该平面ADM则为所求。

其解题过程如下：

将B1C连接，将ME连接。

由于M、E分别是BB1和BC的中点，因此ME∥B1C，且ME=1/2B1C。

又由于N是A1D的中点，因此可得ND=1/2A1D，由题目所给条件可以知道A1B1∥DC且A1B1=DC，那么就可以推出B1C∥A1D且B1C=A1D，最后可得出ME∥ND且ME=ND，符合平行四边形条件，所以四边形MNDE是平行四边形，MN∥ED。而又因为MN不在平面EDC1之内，故可得出结果：MN∥平面C1DE。

通过寻找或者构造出属于它们的交线，该交线必须满足如下条件：

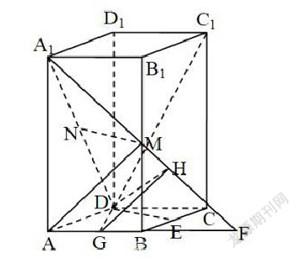
必须经过D点，通过延长A1M来交AB的延长线于点F，这样便可以证明出D、E、F三点共线。

通过证明MN和该交线相互平行，能够证明出B、M分别是AF与A1F的中点，因此，MN∥DF。此为第一小题的解题方法。

对于第二小题，同样是要通过寻找（或是构造出）一个和二面角中的某个半平面相互垂直的平面，而符合这个条件的平面只有平面ABCD与平面ABB1A1，也就是平面ABCD⊥平面ABB1A1。而平面ABCD的角度则为其所求。

此外，还需要在所发现的两个互相垂直的面之内通过另一个平面上面的点来作出AF（此为垂交线）的垂线，接着要过D点去做AF的垂线来交线段AB于点G。

这里需要注意的是，你所做的点绝对不可以是平面棱角上面的点。例如有一部分学生可能会选择D点作为经过的点，但是D点并不在棱A1F上，因此不可选择[1]。

其次，如果点D没有现成的，那么就要作辅助线来选择新的可供垂线所经过的相交点。

在注意上面这两点之后，经过垂足来作出二面角棱的垂线，然后再过G点来作出A1F的垂线，并将其交A1F与点H。

将它们相连接起来，然后计算二面角的正弦值。计算过程是：

GH=3/4AM=3/4√AB2+BM2=3/4√22+22=3√2/2

DG=√3AG=√3

DH=√DG2+GH2=√（√32）+（3√2/2）2=

√15/2

Sin∠DHG=DG/DH=√3·√2/15=（√10）/5

第二小题迎刃而解。

或者也可以使用空間坐标系和空间向量工具来进行解答，过程为：

在得知DE⊥DA的情况下，将D点作为空间直角坐标系原点，向量DA的方向是X轴的正方向，接着可建立相应的空间直角坐标系D-xyz，则此时A坐标为（2，0，0），A1坐标为（2，0，4）M坐标为（1，√3，2），N坐标为（1，0，2），向量A1A为（0，0，-4），向量A1M为（-1，√3，-2），向量A1N为（-1，0，-2），向量MN为（0，-√3，0）。

接着，可设向量m为（x，y，z）作为平面A1MA的法向量，此时， 因此可得：

-x+√3y-2z=0，-4z=0，此时可得=（√3，1，0）。

设向量n为（p，q，r）作为平面A1MN的法向量，则此时

因此可得：

-√3q=0，-p-2r=0，此时可得=（2，0，-1）。

通过求两个空间向量夹角的余弦值的公式可得：

=2√3/2*√5=√15/5

所以可得二面角A-MA1-N的正弦值是√10/5。

这就是通过两种不同的方法来解答该大题第二小题的过程，很明显，使用空间坐标系和空间向量这两种数学工具要比从空间几何逻辑关系中进行探索要简单的多。

对于本空间几何题目的反思：

从总体来看，该空间几何解答题依然是在考察学生的确定性思维，尤其是在求二面角正弦值的过程中，这种考察学生确定性思维的意图愈发明显。学生是否能够通过已经获得的条件来解答出本道题目？这是开启本题正确答案大门的钥匙。

通常，对涉及到几何证明和二面角等空间几何大题的组合，一般是采用分步骤进行确定的“寻找垂直面”、“作出垂直线”、“相连再证明（计算）”这三大步骤。对于前两个步骤来说，它们的目的是为了能够有效寻找到一个在半平面上的合适的点。该店能够在另一个半平面上面作出投影点，这也是求出二面角的关键过程。但是，在第二小题的两种解法中，笔者更加倾向于构建空间直角坐标系并运用空间向量来进行解答，因为向量具有更多更加直观的公式，这些公式将空间中的点与线进行代数化，尤其是将线化为更加直观的数对，这让学生从较难的空间想象过程中得到解放，回归到较为直观简单的代数关系部分，只要用对公式，就能够更快地算出相应结果[2]。也正是因为如此，笔者才在进行有关类似的立体结合问题的讲解中推崇学生们掌握向量法。因为向量法是数形结合方面的一大突破。诚然，有部分教师认为几何法的掌握能够更好地推动学生的解题速度，但是在向量这一更加直观的工具面前，几何法还是要耗费更多的空间思考能力。

参考文献：

[1]孙鋆. 一道立体几何试题的解法探究与拓展[J]. 中学数学月刊， 2017，56（4）：63-64.

[2]王荣峰. 对一道高考题的多方位探究[J]. 中学生理科应试， 2017，23（11）：4-4.