铸件自动打磨用橡胶弹簧的刚度设计

唐遵乐 陈宁宁 王钰

摘要： 针对自动化打磨头在铸件打磨过程中隔振的需要，本研究以一款自动化打磨头为例，通过理论和有限元分析方法，从结构和尺寸上设计了橡胶缓冲弹簧，并根据打磨头本身结构参数，初步确定橡胶缓冲弹簧的尺寸范围。同时，为进一步确定弹簧尺寸，通过控制变量法，在SolidWorks中对不同尺寸参数的橡胶缓冲弹簧进行建模，并对打磨头进行合理简化，利用hypermesh和ANSYS软件，联合对橡胶缓冲弹簧进行静力学分析，并将分析结果的数据点进行曲线拟合，确定弹簧结构尺寸对弹簧刚度的定量影响，根据实际隔振需要和打磨头结构要求，确定弹簧实际外形尺寸。研究结果表明，弹簧刚度与弹簧截面积和内外径比值成正相关，与弹簧高度成负相关。因此，当弹簧高度为15 mm，弹簧外径为120 mm，弹簧内径为13 mm时，满足刚度设计要求。该研究为国内自动化打磨头隔振的研究和铸造业智能化发展提供了重要参考。

关键词： 橡胶缓冲弹簧; 弹簧刚度; 隔振; 控制变量; 有限元分析

中图分类号： U463.33+4.5; U260.331.5  文献标识码： A

一直以来，铸件打磨是工业生产中必不可少的工序，传统的打磨方式是人工手持角磨机进行打磨，虽然效率较高，但打磨工作繁重、粉塵多，对工人的健康极为不利。近年来，国内外研究铸件打磨问题的公司及高校越来越多，推出了一系列自动化或半自动化打磨[14]方案。人工打磨铸件时，人手可以感知打磨力的大小，并调整吃刀量以保证角磨机等部件不受损坏，安装于机器人末端的自动化打磨头，为模仿人手感知打磨力的大小，往往会安装力传感器[58]，力传感器和工业机器人为精密件，因此必须在中间设计缓冲吸振装置，以保护力传感器和机器人。目前，橡胶隔振在美国、日本及国内的建筑业得到广泛应用。橡胶呈现出很多独特的物理和化学特性，其强弹性、大变形，柔软性、耐磨性、绝缘性和阻隔性都十分优良，能满足很大范围的使用要求，同时作为一种粘弹性材料，可通过变形时产生的内部摩擦来吸收振动能量，从而降低振动频率，保护结构不受损坏，具有其他弹性材料无法比拟的优势[914]。因此，本文以自动化打磨头为例，通过理论分析，建立弹簧刚度与结构尺寸的关系，并根据打磨头本身结构参数，初步确定橡胶缓冲弹簧的尺寸范围。打磨过程中的打磨层厚度不同，导致打磨力实时变化，铸件硬质点对砂轮也存在一定的冲击，因此需设计隔振弹簧，对打磨力和冲击进行一定的吸收。为保证隔振效果和安装方便，考虑将橡胶缓冲弹簧安装于力传感器正下方，则打磨点位于橡胶缓冲弹簧外侧，磨削时力传感器和橡胶缓冲弹簧同时受压力和弯曲作用力，从弹簧的刚度和工艺性考虑，将橡胶弹簧设计成圆筒状。该研究满足刚度设计要求，为铸造业智能化发展提供了理论依据。

1 打磨工具结构介绍

打磨工具结构模型如图1所示。本文选取的自动化打磨头主要由力传感器、橡胶弹簧和角磨机组成，橡胶弹簧安装于力传感器和角磨机之间，通过自身变形，吸收打磨时产生的冲击，以保护力传感器、机器人本体和角磨机。打磨工作进行时，主要有两种冲击对硬件造成损坏，一是打磨时设置的砂轮吃刀量过大，超过角磨机的负载，导致砂轮等硬件受力过大，引起变形或损坏;二是打磨过程中，遇到打磨件高点或硬质点时，砂轮会受到冲击。针对这两种冲击力，砂轮打磨时橡胶应有足够大的变形，以保证砂轮和力传感器不受刚性冲击。

另外，砂轮正常打磨时，在工件上需要有一定的下压力，以保证磨削吃刀量，在此正常压力作用下，橡胶弹簧不应有过大的变形，否则将影响打磨深度。以上分析表明，需要确定弹簧合适的刚度，通过变形保证砂轮受冲击时，力传感器和砂轮不会被损坏，且在正常打磨压力作用下，不会有很大变形，保证打磨效果。

2 影响橡胶弹簧刚度的因素分析

根据前述，缓冲弹簧为圆筒状结构，主体材料为橡胶，端面镶嵌带螺纹孔的金属块，用于与其他部件连接。打磨头对铸件进行打磨时，砂轮前端同时受支反力和摩擦力，对砂轮和力传感器的破坏主要是冲击时的支反力，此处只考虑支反力。砂轮受力点离橡胶弹簧中心有一定的距离，受力变形属于偏压杆问题，即橡胶弹簧同时受压力和弯曲作用力。分析时不考虑砂轮本身的变形，可将弹簧末端磨头部分简化为钢板形式，弹簧受力模型如图2所示。

由式（4）可以看出，砂轮轴向位移主要是由弹簧受压变形和受弯矩截面转角引起，压缩变形由弹簧高度、弹性模量和截面积决定，截面转角的大小，除了与弹簧高度、弹性模量和截面积有关外，还与弹簧内外径比值α有关，弹簧的弹性模量E由材料决定，因此需要通过分析弹簧高度、截面积和内外径比值α对砂轮轴向位移的影响，最终确定橡胶弹簧的结构尺寸。

2.4 橡胶弹簧结构尺寸的设计分析

根据打磨路径规划，砂轮吃刀量设为0.4 mm，在此打磨量下，力传感器测得磨头在打磨过程中受到的支反力约为50 N，为保证砂轮有足够吃刀量，弹簧变形不应超过吃刀量的1/3，即0.13 mm，打磨中受到的冲击约为打磨时的4倍，即200 N左右，为保护力传感器弹簧变形，应超过打磨深度，即0.4 mm。

根据前述可知，影响弹簧综合刚度的变量有弹簧高度、截面积和内外径比值α，通过控制变量法，研究弹簧刚度和三者之间的关系，并选择合适的参量。由于弹簧实际本身变形时不能忽略端面金属块的影响，此时解析法不适用，对模型简化后，可利用hypermesh和ANSYS，联合分析求解不同参量下砂轮打磨点的轴向位移作为橡胶刚度选择的依据[1518]。

3 基于有限元的分析与设计

3.1 有限元模型的建立

通过有限元仿真计算，确定柱形橡胶弹簧在径向和轴向上的优化尺寸，获得满足刚度值需要的结构尺寸。

1） 计算模型的建立。该橡胶弹簧主要承受轴向压力和倾覆力矩。为方便计算，根据结构形式和受力情况，将磨头底部简化为长方体模型。考虑橡胶材料，在小变形条件下，由弹性理论模型，可近似的把它当成弹性材料处理[1920]，本研究中橡胶弹簧的弹性模量取E=6.1 MPa，泊松比取μ=0.49。为提高计算精度，将模型划分为六面体网格，单元类型选择Solid185单元，该单元具有粘弹、大变形和应力钢化等特点，能够满足对橡胶弹簧性能的模拟。

2） 约束的建立。弹簧通过螺钉与两端固定板连接，工作时端面与固定板保持贴合。因此，建立约束时在螺

纹孔处建立mass21单元，利用rigids单元与固定板连接，将弹簧固定端端面约束轴向和绕径向转动自由度，利用Contact manager建立MPC面接触单元，对弹簧自由端端面进行约束。

3） 等效载荷的设定，打磨头工作时，不考虑重力影响，弹簧受力主要来自于砂轮前端所受的支反力和摩擦力，其中摩擦力为径向力，对砂轮轴向变形无明显影响，在此不予考虑。支反力作用在砂轮前端打磨点处，面积较小，可等效为有限元模型中钢板前端中点受相同大小的力。在钢板前端中点位置上分别施加50 N和200 N的静载荷，观察弹簧变形情况。有限元模型如图3所示。

3.2 橡胶弹簧结构尺寸的分析计算

本研究中的橡胶弹簧除满足刚度要求外，作为打磨头的结构件，还需满足安装方便和结构紧凑等尺寸要求。根据力传感器及其他部件的尺寸结构，橡胶弹簧外径应在90～120 mm之间，高度在15～35 mm之间。在此条件下，分别研究弹簧刚度与截面积、高度和内外径比值间的关系。

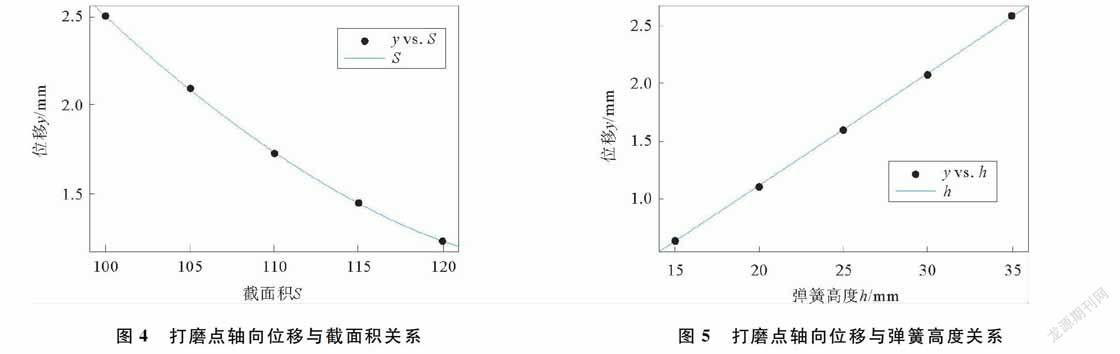
1） 截面积对刚度影响的分析计算。取弹簧高度为30 mm，內外径比值α为1/5，以图3所示的模型做受支反受力200 N，外径分别为100，105，110，115，120 mm的有限元分析，打磨点轴向位移与截面积关系如图4所示。图4中，y为位移，S为弹簧外径。

2） 高度对刚度影响的分析计算。以内径21 mm，外径105 mm的橡胶弹簧为研究对象，保持弹簧截面积和内外径比值α不变的情况下，以有限元模型做受支反力200 N，高度分别为15，20，25，30，35 mm的有限元分析，打磨点轴向位移与弹簧高度关系如图5所示。图5中，y为位移，h为弹簧高度。

3） 内外径比值对刚度影响的分析计算。取弹簧高度为30 mm，截面积为2 646π，以图3所示的模型做受力200 N，内外径比值α分别为1/7，1/6，1/5，1/4，1/3的有限元分析，打磨点轴向位移与内外径比值关系如图6所示。图6中，y为位移，a为内外径比值。

4） 内外径比值对刚度影响的分析计算。取弹簧高度为30 mm，截面积为2 646π，以图3所示的模型做受力200 N，内外径比值α分别为1/7，1/6，1/5，1/4，1/3的有限元分析，打磨点轴向位移与内外径比值关系如图6所示。图6中，y为位移，a为内外径比值。

由图4～图6可以看出，弹簧刚度与弹簧截面积和内外径比值成正相关，与弹簧高度成负相关。因此，缓冲弹簧可设计为矮筒、大内外径比值的形状，这样可以保证刚度，且节省材料、结构紧凑。结合本文橡胶弹簧结构尺寸的限制要求，为使整体结构协调紧凑，优先选择降低弹簧高度，即弹簧高度选为15 mm，其次选择大的内外径比值以减少弹簧截面积，节省材料，故弹簧外径选为120 mm，内径根据弹簧刚度设计要求确定。当弹簧受冲击力为200 N时，砂轮打磨点轴向位移应大于0.4 mm的设计要求，综合前述中弹簧高度取30 mm，外径取120 mm，内径24 mm时，弹簧在200 N冲击力下打磨点轴向位移值为1.32 mm，且弹簧刚度与高度关系的变形曲线趋于正比例的关系的分析结果，可以得出弹簧内径应小于24 mm。

当弹簧外径为120 mm，高度为15 mm时，分别取弹簧内径为5，10，15，20，25 mm，以有限元模型做受支反力200 N的有限元分析，据此分析橡胶弹簧内径对弹簧刚度的影响，打磨点轴向位移与内径的关系如图7所示。图7中，y为位移，d为弹簧内径。由图7可以看出，弹簧刚度与内径值大小成负相关，且随着内径增大，影响系数逐渐增大。图7中，曲线与打磨点轴向位移值为0.4 mm，相交时弹簧内径为12.5 mm左右。

50 N静力下打磨点位移图如图8所示，200 N静力下打磨点位移图如图9所示。由图8和图9可以看出，弹簧内径取13 mm，在此结构尺寸下，打磨点在50N和200 N静力下，轴向位移分别为0.100 22 mm和0.400 882 mm，即满足了刚度设计要求。

4 结束语

本文基于一款自动化打磨头，设计了橡胶隔振弹簧，通过理论分析，讨论了影响弹簧刚度的结构尺寸因素，同时通过控制变量的方法，利用有限元分析了在不同结构尺寸下的弹簧的刚度，建立了结构尺寸与弹簧刚度的关系模型，给出满足刚度和结构要求的弹簧尺寸，分析在正常打磨和冲击作用下，打磨点的轴向位移值。本研究为橡胶弹簧在自动化打磨中隔振的应用提供了理论基础。

参考文献：

[1] 陈跃城， 刘伟.铸件清理打磨自动化技术及其应用[J]. 铸造设备与工艺， 2015（5）： 16.

[2] Hamid N， Gunnar B. A process model for robotic disc grinding[J]. International Journal of Machine Tools and Manufacture， 1995， 35（4）： 503510.

[3] 贾时成， 孙英飞. 国产工业机器人打磨系统设计[J]. 中国新技术新产品， 2014（4）： 149150.

[4] 徐琤琤. 工业机器人在铸铁件打磨中的应用研究[J]. 热加工工艺， 2016， 45（23）： 106108.

[5] 缪新， 田威. 机器人打磨系统控制技术研究[J]. 机电一体化， 2014（11）： 814.

[6] 赖火生， 吴磊， 陈新度， 等. 机器人实现未知参数下的曲面跟踪和恒力控制的研究[J]. 制造技术与机床， 2018（6）： 2125.

[7] Masato O， Yasushi K， Ryosuke M. Electrode for force sensor of conductive rubber[J]. Journal of Sensor Technology， 2012， 2 （3）： 127131.

[8] Maria G D， Natale C， Pirozzi S. Force/tactile sensor for robotic applications[J]. Sensors and Actuators A Physical， 2012， 175： 6072.

[9] 黄奇鹏， 武文斌， 张豪， 等. 惯性往复振动去石机双向等量刚度的橡胶支撑弹簧设计[J]. 粮食加工， 2018， 43（1）： 5154.

[10] 鲍玉新， 李永志， 王淑军， 等. 振动筛用橡胶弹簧的设计与计算[J]. 煤矿机械， 2008， 29（2）： 68.

[11] Xu Y J， Liu Y B， Kan C Z， et al. Experimental research on fatigue property of steel rubber vibration isolator for offshore jacket platform in cold environment[J]. Ocean Engineering， 2009， 36（8）： 588594.

[12] stberg M， Coja M， Kari L. Dynamic stiffness of hollowed cylindrical rubber vibration isolatorsThe waveguide solution[J]. International Journal of Solids and Structures， 2013， 50（10）： 17911811.

[13] Kenichiro A， Takahiro T， Yuki A. Development of displacementdependent rubber bush for yaw damper to prevent carbodyvertical vibration[J]. Quarterly Report of RTRI， 2017， 58（3）： 182188.

[14] Eunsoo C， Heejung Y， Kyoungsoo P. Vibration tests of precompressed rubber springs and a flagshaped smart damper[J]. Engineering Structures， 2017， 132： 372382.

[15] 樊光辉. FRP橡胶支座竖向力学性能有限元分析[J]. 广东建材， 2018， 34（2）： 4143.

[16] 朱明， 宋满华. 扁平橡胶密封结构对比及有限元分析[J]. 失效分析与预防， 2018， 13（1）： 2528.

[17] 张治国， 郑明军， 谢基龙. 弹性车轮瞬态动力响应的有限元仿真方法研究[J]. 北方交通大学学报， 2003， 17（1）： 2527， 35.

[18] Han X P， Liang J G， Dong X L， et al. The rubber spring characteristics test of the main vibration spring in horizontal vibrating centrifuge[J]. Journal of the Chinese Ceramic Society， 2013， 38（4）： 700706.

[19] 李曉芳， 杨晓翔.橡胶材料的超弹性本构模型[J]. 弹性体， 2005， 15（1）： 5058.

[20] 朱武， 李超. 隔震橡胶块两种模型的有限元比较分析[J]. 青岛科技大学学报： 自然科学版， 2011， 32（1）： 7275.