在学习活动中发展数学思维

程金凤

摘要：苏教版小学数学四年级下册《三角形的三边关系》一课是小学阶段一节探索性很强的课。如何遵循学生的年龄特点和认知规律，引导学生在多种数学活动中，自主探究、发现三角形的三边关系，在获得知识的同时发展数学思维？从以下几个方面进行了探索：问题聚焦，指引思维;自主探究，深化思维;反思追问，完善思维;解释应用，提升思维。

关键词：学习活动数学思维三角形的三边关系教学设计

数学是思维的体操。发展学生的数学思维是数学教学非常重要的目标。苏教版小学数学四年级下册《三角形的三边关系》一课是小学阶段一节探索性很强的课。如何遵循学生的年龄特点和认知规律，引导学生在多种数学活动中，自主探究、发现三角形的三边关系，在获得知识的同时发展数学思维？我从以下几个方面进行了探索。

一、问题聚焦，指引思维

教师要充分了解学生的学情，在关键处创设情境，进行问题聚焦，指引学生思维的方向。

本节课的关键是，怎样引导学生关注三角形两边长度的和与第三边的关系。而三角形的三边关系与“两点之间线段最短”的原理是一致的，这就要求设计的数学活动能促使学生把三角形中的两条边作为一个整体和第三条边去比。

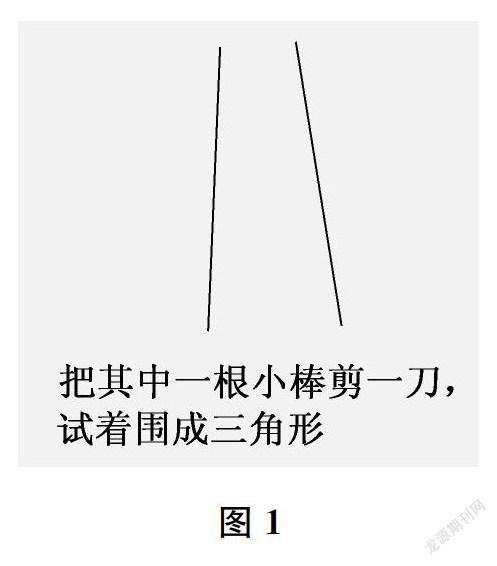
由此，上课伊始，我安排了活动一（如下页图1），出示两根一样长的小棒，让学生把其中一根剪一刀，试着围成三角形。在学生独立操作都围不成三角形时，我放大这种情形：“谁愿意到前面来试一试？是不是真的围不成三角形？”“为什么围不成三角形呢？”问题驱动促使学生把实践操作与数学思考结合起来。在我的引导下，学生反复操作、交流总结：“把其中一根小棒剪一刀后，要想围成三角形，就要把这两剪开的根小棒往上提，但只要往上提一点点，就会出现缺口。”此时，我配合具体的操作和动态的演示，使学生进一步明确：两根小棒的长度之和等于第三根小棒的长度时，不能围成三角形。

图1

然后，我追问：“要想围成三角形，可以怎么办？”“能不能围成三角形，都是把谁和谁比较的？”在我的步步追问下，学生交流明确：要把两边长度的和与第三边比较。问题聚焦引发了学生的思考，明晰了研究的方向，为深入探究三角形的三边关系铺平了道路。

二、自主探究，深化思维

学生对图形性质的体验是建立在数学实践活动基础上的。课堂上，教师要为学生提供观察、操作、思考、想象、交流等活动的机会，使得他们在自主探究中体验三角形的三边关系，积累数学活动经验，发展空间观念，深化数学思维。

本节课，在学生明确了要把两边长度的和与第三边做比较后，我安排了活动二（如图2），让学生在自主探究中总结得出三角形的三边关系。为了便于学生在操作中发现围成与围不成的各種情况，我将教材中“8 cm、5 cm、4 cm、2 cm”的4根小棒换成“8 cm、5 cm、4 cm、3 cm”的4根小棒。

图2

学生有序思考、自主选择，用“8 cm、5 cm、4 cm”“8 cm、5 cm、3 cm”“8 cm、4 cm、3 cm”“5 cm、4 cm、3 cm”4组小棒，分别围三角形，并填写活动记录单。学生通过实际操作，在头脑中形成了直观的思维表象，并在此基础上建立了“围三角形”的模型（各种情况的实物图），为深度思维提供了形象支撑。在围成与围不成的观察、计算、比较中，学生深入探究三角形的三边关系。在实物语言、符号语言与文字语言的相互转换过程中，学生感悟发现：三角形两条短边长度的和大于第三条边。

从没有规定小棒长度的操作演示到有数据支撑的验证，学生经历了由直观到抽象的推理过程，发展了空间观念，深化了数字思维。这不仅符合学生的年龄特点，也顺应了学生的认知规律。

三、反思追问，完善思维

学生探究后的发现往往是零散的、片面的、有缺陷的。教师要结合具体情境进行追问，引导学生不断反思，逐步完善思维。

本节课，学生在自主探究中，能够发现“三角形两条短边长度的和大于第三条边”的规律，但是很难得出“三角形任意两边长度的和大于第三边”的结论。因此，在研究“围成三角形”时，我适时追问：“围成三角形的三条边中仅仅存在这一组不等关系吗？”引导学生发现：不仅仅是两条短边大于第三条边，“每两条边”或“随便哪两条边”与第三条边都存在这样的关系;在研究“围不成三角形”的情况时，我适时追问：“已经有两边长度的和大于第三边了，怎么还围不成三角形呢？”随着学生不断地发现，自然得出：三角形任意两边长度的和大于第三边。学生在冲突中反思，在反思中完善，正是因为有了充分的思维碰撞，得出的结论才更加全面。

教学中，教师还可以通过追问“是不是任意的三角形每两边长度的和都大于第三边”，引导学生举例（任意画一个三角形）验证，强化学生对于“任意”的理解。

四、解释应用，提升思维

对所学的知识进行解释应用，能够进一步提升学生的思维。这对练习的要求比较高：应层层深入，步步提升。

本节课，在“判断哪一组线段可以围成三角形”的基础练习中，我引导学生自主发现判断能否围成三角形的更简洁的方法：只要较短的两条边的长度和大于第三条边，就可以围成三角形。随后的快速判断练习，使学生的分析能力、归纳能力得到螺旋提升。紧接着，学生在生活应用练习“走哪条路最近”中体验了这一新知的应用，同时沟通了与“两点之间线段最短”这一旧知的联系;在拓展延伸练习“小狗的三角形房顶的第三条边可以是多少分米”中，既体验了三角形三边关系的应用价值，又把三角形的三边关系转化为“三角形任意两边之差小于第三边”，同时渗透了勾股定理等数学知识。

真实生动、数形结合的情境，使学生深刻感受到生活中处处有数学，有直观的视觉冲击，更有深度的数学思考，使学生的思维在巧妙的设疑中不断提升。