基于云模型和风险矩阵的自然灾害风险评价
2019-09-10洪成王桂生周家贵徐艳
洪成 王桂生 周家贵 徐艳


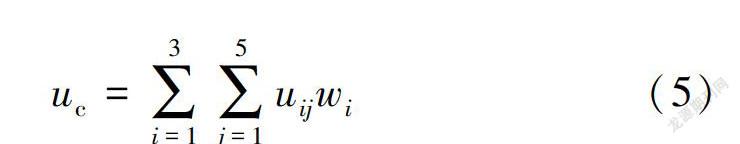
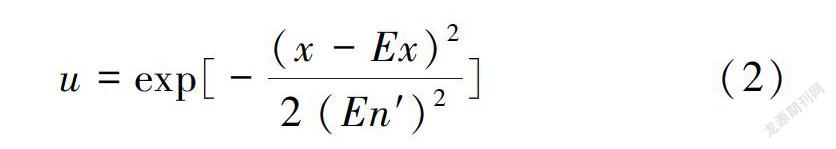


摘要:自然灾害风险具有模糊性和随机性等不确定性特点,基于云模型和风险矩阵理论的自然灾害风险评价新方法可综合分析评价其模糊性和随机性。模型先根据自然灾害风险评价指标分级标准,计算各指标隶属于不同自然灾害风险等级的云数字特征值,再结合正向高斯云算法和各指标之间的合成风险矩阵,最终确定评价区域的综合自然灾害风险等级。基于全国31个省级行政区自然灾害实例的计算结果表明,该模型应用于自然灾害风险评价是可行有效的,且计算简便,结果可靠,为分析解决类似问题提供了新的研究思路。
关键词:自然灾害;风险评价;不确定性分析;云模型;风险矩阵;随机性
中图分类号:X43
文献标志码:A
doi: 10.3969/j.issn.1000- 1379.2019.06.004
1 引言
自然灾害是自然要素和人类社会经济要素相互作用的结果,具有自然和社会双重属性,它造成的损失程度既受自然灾害种类(如地震、洪水和台风等)危险性的影响,也取决于承灾体(经济社会系统)的脆弱性。区域自然灾害危险性越大、承灾体(经济社会系统)越脆弱,自然灾害造成的损失越大,自然灾害风险就越高。准确评价区域的自然灾害风险,可为制定科学合理的经济社会发展规划提供依据,对于制定主动的防灾减灾战略、进行积极的风险管理具有重大意义。目前,自然灾害的风险评价方法较多,如模糊分析法[1-2]、投影寻踪法[3]、神经网络法[4]、灰色关联法[5-7]等,这些方法在实际应用中取得了一定效果,但都不可避免地面临数据和指标的模糊性和随机性问题,至今尚未找到综合考虑这两种不确定性难题的有效方法。云模型( Cloud Model)理论可充分考虑定性概念所包含的不确定性和离散性,实现定性语言与定量表示之間的有效转换,从而克服传统评价方法在处理模糊性和随机性方面的不足[8]。云模型理论已应用于水资源及其他资源的短缺风险评价中,但在评价过程中较难完全反映风险系统中各风险要素的作用机制。风险矩阵是通过定性分析和定量分析,综合考虑风险发生概率和风险影响两方面因素构造的,通过风险矩阵可确定风险评价等级和风险评价结果,其核心思想是根据风险发生概率与风险影响之间相互作用的情况,确定风险评价等级结果。本文基于云模型和风险矩阵理论探讨自然灾害风险评价的新模型,使其综合考虑风险评价过程中存在的模糊性与随机性,同时基于灾害损失风险形成机制构建各评价指标之间的合成风险矩阵,并以全国31个省级行政区(不含港澳台)的自然灾害风险实例验证该方法的有效性。
2 云模型理论
云模型理论是李德毅等[8]提出的一种实现定性概念与定量数值之间双向转换的模型,目前已在数据挖掘、信任管理和综合评价等多个领域得到广泛应用[9-13]。
2.1 云的定义
设U是一个定量论域,可用实数值表示,C是U上的定性概念,若存在定量数值X∈U,且x是C的一次随机实现,x对C的确定度u(x)∈[O,1]是有稳定倾向的随机数,即‘8,14]:
u:U→[0,1] (Vx∈U,x→u(x)) (1)则x在论域U上的分布u(x)称为云,每一个x称为一个云滴。从这一云的定义中可知,云模型理论是一种研究定性问题定量化的方法。云滴的确定度反映了模糊性,该值本身又是个随机值,可以通过其概率分布函数来描述[8]。
2.2 云模型的数字特征
定性概念的整体特性可用云的数字特征来反映,这是定性概念的整体定量特性,对定量描述定性概念的内涵和外延有着极其重要的意义[8]。一个概念可由云模型的期望Ex、熵En和超熵He三个数字特征值来整体表征[8-9]:期望E用于度量定性概念的基本确定性,它表示云滴在论域空间分布中的数学期望:熵En用于度量定性概念的不确定性,它由定性概念的随机性和模糊性共同决定,熵不仅可以度量定性概念的随机性,反映云滴的离散程度,同时还是隶属于这个定性概念的度量,决定了论域空间中可被概念接受的云滴的确定度:超熵He是熵的熵,用于度量熵的不确定性,论域空间代表该语言值的所有点的不确定度的凝聚性可由超熵反映,云滴的厚度可由其值的大小间接反映。
2.3 云算法
3 基于云模型和风险矩阵的自然灾害风险评价方法
自然灾害风险评价中,1个云滴可映射一次具体评价过程。根据选取的自然灾害风险评价指标及其等级标准集,自然灾害风险可分为n个等级,每个综合云用于表示每一个评价指标隶属于某一风险等级的确定度。
本文将云模型应用于自然灾害风险评价之中,需作以下两点假定[9,15]:①把一个自然语言的概念赋予每一定量的自然灾害风险等级,每个风险等级可映射成一朵云:②待评样本的实例数据隶属于某一风险等级的确定度的分布,假定服从高斯分布。
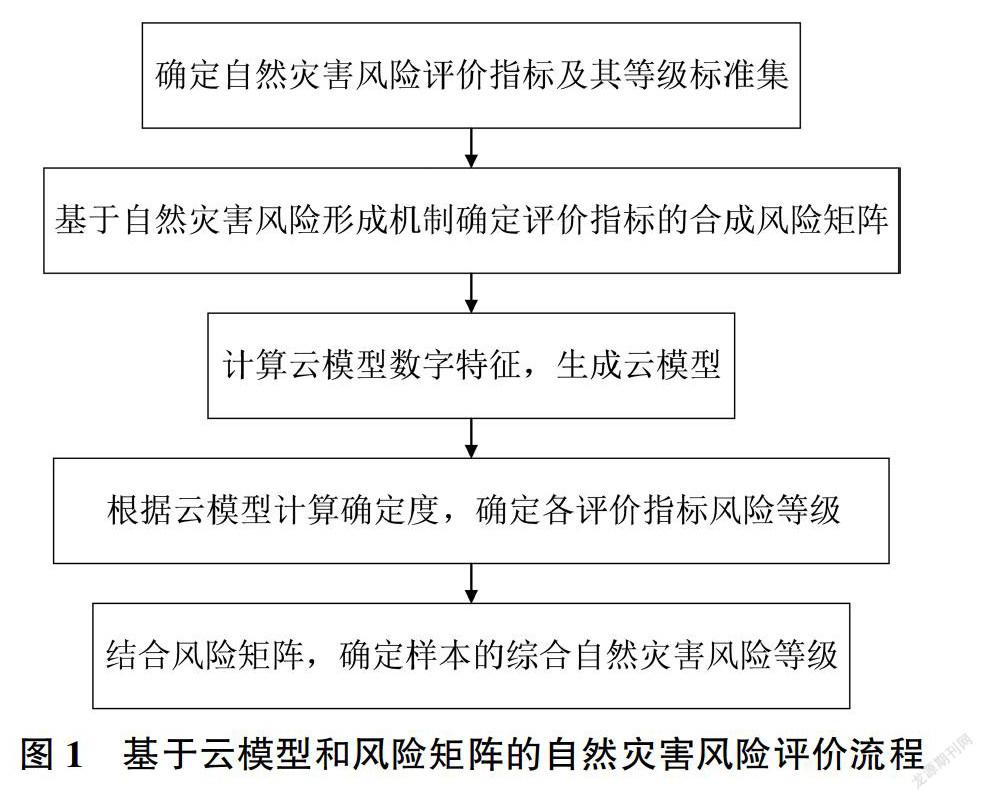
根据上述两点假定,基于云模型和风险矩阵的自然灾害风险评价方法的实现过程见图1。①确定适当的自然灾害风险评价指标及其等级标准集:②基于自然灾害风险系统形成过程中各系统要素的作用机制,确定①中各评价指标之间的合成风险矩阵:③根据①中确定的等级标准集计算各风险等级的3个云数字特征值,再依据En和En'生成用于构成云滴的高斯分布随机数,并由正向高斯云算法生成某评价指标隶属于某一自然灾害风险等级的云模型:④读取待评样本的实例数据,计算各评价指标属于各风险等级的确定度,确定度值最大的等级即为该指标的风险等级:⑤结合②中构建的风险矩阵,得到待评样本的综合自然灾害风险等级。
4 实例应用
以全国31个省级行政区的自然灾害风险评价为计算实例16],验证上述云模型和风险矩阵理论在自然灾害风险评价中的有效性。
4.1 自然灾害风险评价指标及其标准的确定
首先确定全国31个省级行政区的自然灾害风险评价指标及其等级标准,然后产生各指标隶属于各风险等级的云模型。由于区域自然灾害风险评价需衡量的因素较为复杂,不同区域的致灾因子强度(自然条件)和承灾体脆弱性程度(经济社会条件)差异较大,因此从区域自然灾害的危险性和脆弱性两方面综合考虑,选择评价指标体系[16]。
(1)灾害危险性指标。选取地震、地质、洪水和台风4种自然灾害,具体数据见表1。
(2)承灾体(经济社会系统)脆弱性指标。该指标由承灾体的经济、人口、财产等因素共同决定,可将其分为经济脆弱性和社会脆弱性。笔者选取国内生产总值、全社会固定资产投资作为经济脆弱性评价指标,选取人口密度作为社会脆弱性评价指标,具体数据见表1。
灾害危险性指标s.由4种自然灾害地震、地质、洪水和台风的危险度综合而成:经济脆弱性指标s,由国内生产总值和全社会固定资产投资综合而成:社会脆弱性指标s,由区域人口总数(万人)和区域面积(104km2)综合而成。评价指标s1、s2、s3的具体计算公式见文献[16],计算结果见表1。
灾害危险性指標s1、经济脆弱性指标s:和社会脆弱性指标s3构成了全国31个省级行政区自然灾害风险评价的指标体系。3个评价指标的风险等级标准可由距平百分率P确定[16]:
P=指标一平均值 × 100%
(3)
平均值
式中:平均值为某评价指标的全国平均值。
将各评价指标的风险分为5级:当P≤-20%时为极低风险,-20%
4.2 构造自然灾害风险评价指标的合成风险矩阵
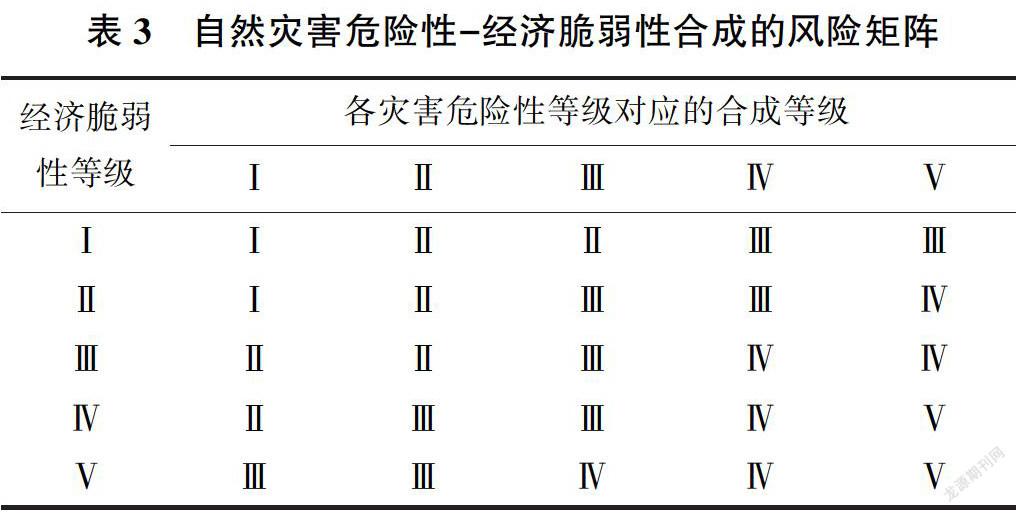
自然灾害危险性一经济脆弱性合成的风险矩阵见表3。自然灾害危险性等级与承灾体经济脆弱性等级相同时,取合成等级与危险性和脆弱性的等级相同:灾害危险性等级与经济脆弱性等级相差一级时,考虑到自然灾害的危险性是灾害损失风险形成的首要条件,是风险系统输入,其对区域自然灾害风险形成机制的作用更为明显,故取合成等级与危险性等级相同,例如,若危险性等级为I级(极低风险),脆弱性等级为Ⅱ级(低风险),则合成等级为I级(极低风险);灾害危险性等级与经济脆弱性等级相差两级时,取合成等级介于危险性和脆弱性等级之间,例如,若危险性等级为I级(极低风险),脆弱性等级为Ⅲ级(中等风险),考虑到危险性与脆弱性对风险形成的综合影响,则取合成等级为Ⅱ级(低风险);灾害危险性等级与经济脆弱性相差三级时,考虑到灾害危险性风险系统输入的首要作用,故取合成等级介于危险性和脆弱性等级之间且稍偏于危险性等级,例如,若危险性等级为I级(极低风险),脆弱性等级为Ⅳ级(高风险),则合成等级为Ⅱ级(低风险);灾害危险性等级与经济脆弱性等级相差四级时,取合成等级介于危险性和脆弱性等级之间,例如,若危险性等级为I级(极低风险),脆弱性等级为V级(极高风险),考虑到危险性与脆弱性对风险形成的综合影响,则取合成等级为Ⅲ级(中等风险)。
基于上述合成规则,自然灾害危险性一社会脆弱性合成的风险矩阵和自然灾害危险性一经济脆弱性与灾害危险性一社会脆弱性合成的风险矩阵分别见表4和表5。
与传统的指标权重法相比,风险矩阵方法更能充分体现自然灾害风险系统中各要素之间的作用机制。具体地说,如对于表3中灾害危险性和经济脆弱性指标,若采用传统权重法,两者的重要程度仅通过2个指标的权重体现,关系相对固定;而采用风险矩阵法,通过2个指标在各自风险等级下的合成法则,能完全反映它们之间的等级关系随各指标风险等级的变化过程,两者的重要程度因各指标所处风险等级不同而改变,更具灾害风险形成机理性。
4.3 云模型数字特征值的计算
基于已确定的全国31个省级行政区自然灾害风险评价指标及其等级标准,可采用式(4)计算得到所需的3个云模型数字特征,如对于某一具有上下边界的评价指标s( [Amin,Amax]),3个云模型数字特征值可通过下式得到[10.15]。式中:Amin、Amax分别为评价指标s的最小与最大边界;k为常数,可通过评价指标的模糊阈度进行适当调整,本文取0.01。
而对于单边界限的某评价指标,形如S[Amin,+∞]或[一∞,Amax],可先通过实例样本数据的上下限确定其缺省边界参数或期望值,再依据式(4)计算云模型数字特征值。本文最终采用的云模型数字特征值计算规则见表6。
表6中的参数a至e分别为全国31个省级行政区自然灾害风险评价指标等级标准的各边界值。如某评价指标s的5个评价区间为:(0,a]、(a,b]、(b,c]、(c,d]、(d,e]。以评价指标灾害危险性s1为例,各参数值分别为a= 0.602,6=0.677,c=0.827,d= 0.902,e=1.000n
4.4 评价指标云模型的生成
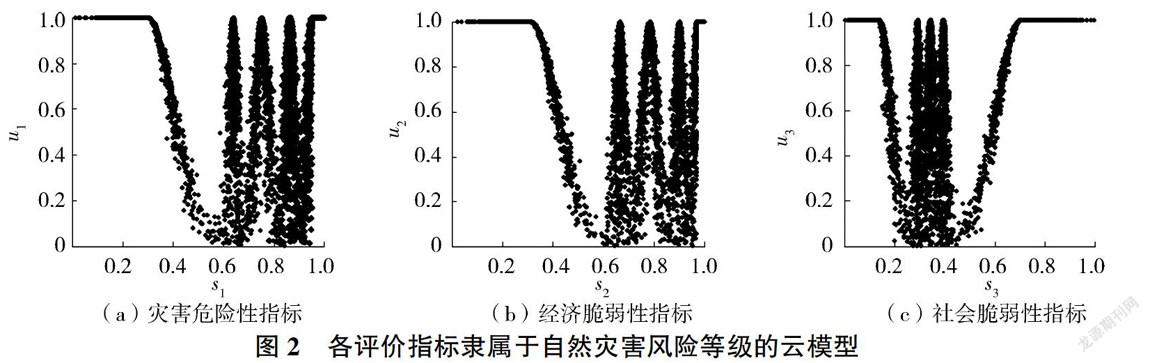
基于云模型理论确定的3个数字特征值(Ex,En,He),运用正向高斯云算法按照3个自然灾害风险评价指标生成相应的云图,如图2所示,图2中横坐标表示的是某评价指标的取值,纵坐标表示的是该指标对应的确定度。图2(a)、(b)、(c)中,从左至右分别代表3个评价指标自然灾害风险等级I至V对应的云,其中,处于风险等级I左半区间(0,a/2]和等级V右半区间((d+e)/2,e]的各评价指标值,其确定度均为1,即完全隶属于该风险等级,故呈“半云”状。
可通过正向高斯云算法计算全国31个省级行政区自然灾害风险评价的3个指标实例数据隶属于某云的确定度,且确定度值最大的等级即为各指标的风险等级,再依据表3、表4和表5中各评价指标之间的合成风险矩阵规则,最终得到各行政区的综合自然灾害风险等级。如:某地区灾害危险性的指标值隶属于风险等级Ⅲ的确定度最大,则该指标处于中等风险(Ⅲ);若该地区经济脆弱性指标处于低风险(Ⅱ),社会脆弱性指标处于高风险(Ⅳ),则先根据表3得到灾害危险性一经济脆弱性合成的风险等级,为中等风险(Ⅲ),再根据表4得到灾害危险性一社会脆弱性合成的风险等级,为中等风险(Ⅲ),最后根据表5中的合成规则得到3个指标的综合风险等级,为中等风险(Ⅲ)。
若采用传统的权重分配法,则将各指标隶属于某云的确定度分别乘以相应评价指标的权重,最终计算得到综合确定度u。根据最大的综合确定度值,判别全国31个省级行政区的自然灾害风险等级[9,l5],计算公式为
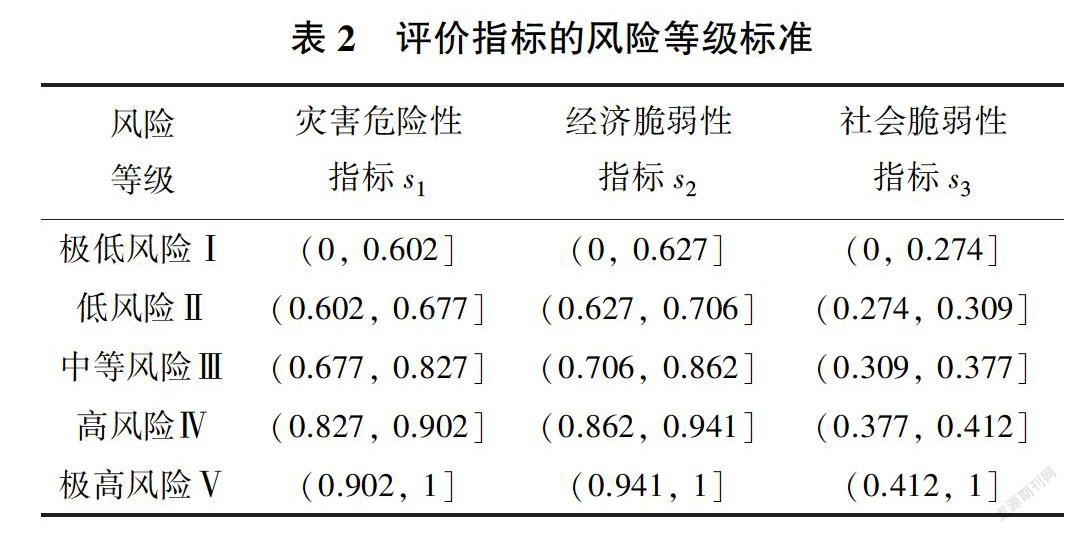
采用文献[16]中的数据验证所构建模型的正确性和有效性。实例中全国31个省级行政区的自然灾害风险评价选用了灾害危险性、经济脆弱性和社会脆弱性3个指标,风险等级分为极低风险I、低风险Ⅱ、中等风险Ⅲ、高风险Ⅳ和极高风险V,各评价指标实例数值和风险等级标准分别见表1、表2。
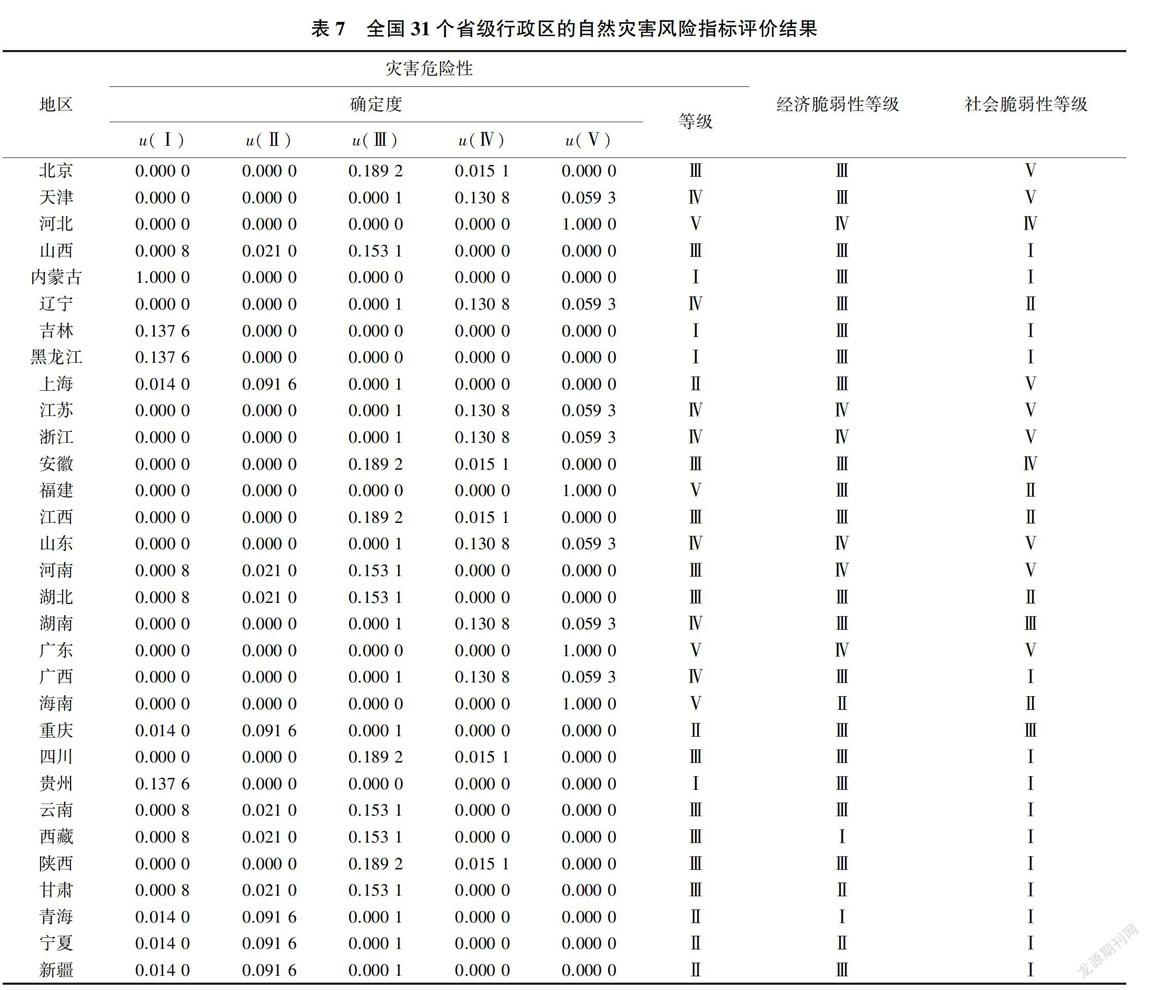
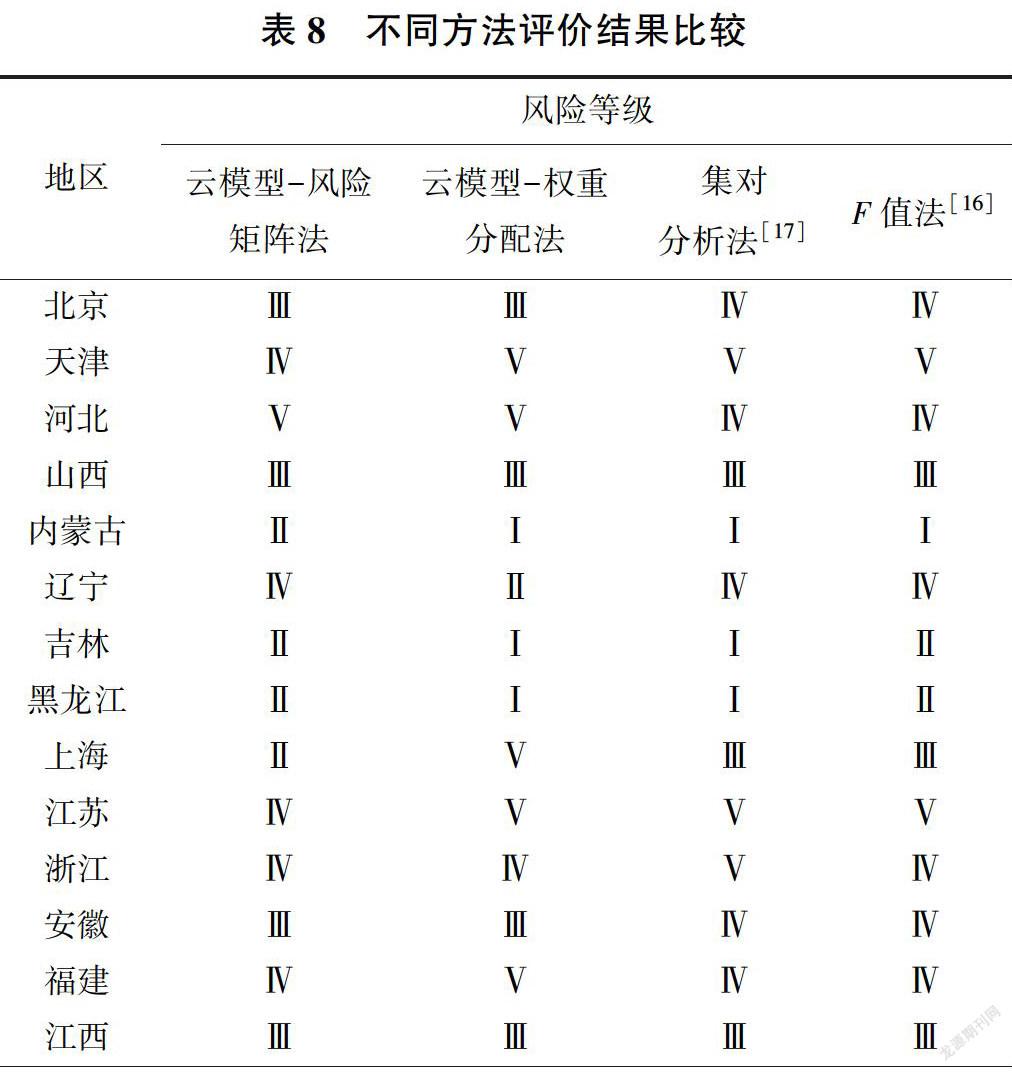
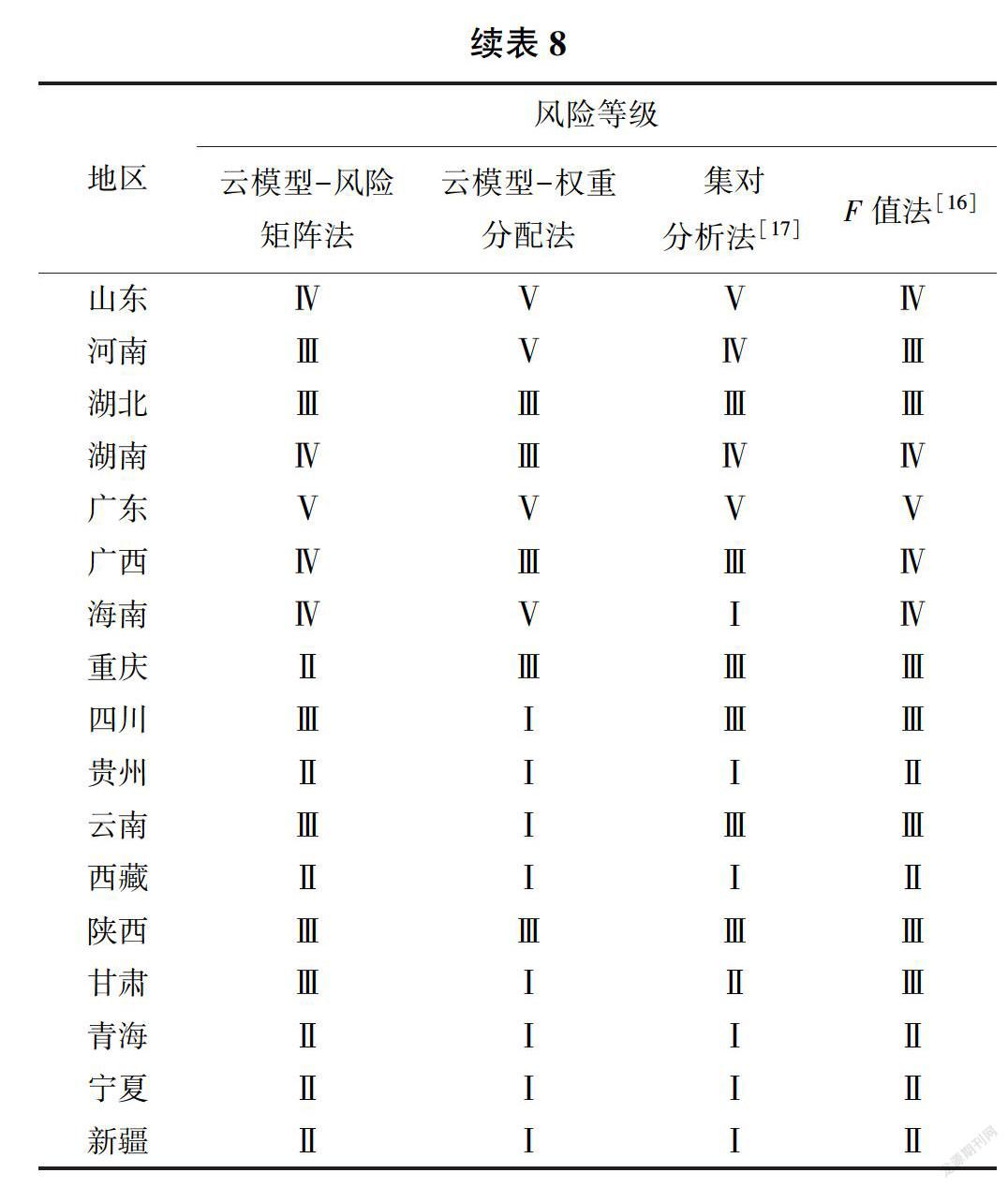
基于上述自然灾害风险评价模型和表1,可得到各评价指标对应的风险等级标准上下界限值Amin和Amax,代人式(4)可以计算自然灾害5个风险等级的云模型数字特征值,并生成每个评价指标隶属于某一风险等级的云图。由式(2)和全国31个省级行政区自然灾害风险评价的实例指标值,计算其在风险等级的确定度,确定各指标的风险等级,然后依据表3、表4和表5,可得到全国31个省级行政区的综合自然灾害风险等级。基于云模型的3个自然灾害风险指标的评价结果见表7,基于云模型和风险矩阵的自然灾害风险评价结果及与其他方法的评价结果比较见表8。在此以北京的自然灾害风险(s1=0. 800,s2=0.800,s3=1. 000,表1)说明实际确定度的计算过程。由正向高斯云算法得到s.灾害危险性评价指标隶属于5个风险等级的确定度:μI=μⅡ=μv=0,μⅢ=0. 189 2,μIV=0. 015 1(表7),反映到实际情况中,s1=0.800应隶属于风险等级Ⅲ,而计算结果μⅢ>μIv>μI=μⅡ=μv,表明s1= 0.800隶属于风险Ⅲ级的程度较大,不隶属于其他的风险等级,符合实际。同理可计算得到经济脆弱性指标和社会脆弱性指标对某一风险等级的确定度,其中,经济脆弱性指标s2=0. 800隶属于风险Ⅲ级的程度较大,社会脆弱性指标s3= 1.000隶属于风险V级的程度较大,均与实际相符。再根据表3、表4和表5,灾害危险性一经济脆弱性合成为风险Ⅲ级,灾害危险性一社会脆弱性合成为风险Ⅳ级,最终灾害危险性一经济脆弱性和灾害危险性一社会脆弱性合成为风险Ⅲ级(表8)。
由表8可知,全国31个省级行政区中自然灾害风险等级为I的地区有0个:等级为Ⅱ的地区有10个,分别为内蒙古、吉林、黑龙江、上海、重庆、贵州、西藏、青海、宁夏和新疆;等级为Ⅲ的地区有10个,分别为北京、山西、安徽、江西、河南、湖北、四川、云南、陕西和甘肃;等级为Ⅳ的地区有9个,分别为天津、辽宁、江苏、浙江、福建、山东、湖南、广西和海南;等级为V的地区有2个,为河北和广东。
为验证本文所建立评价模型的有效性,将本文的评价结果与F值法[16]和集对分析法[17]以及云模型一权重分配法的自然灾害风险评价结果作了比较分析。由表8可知,本文风险评价结果与集对分析法和云模型一权重分配法的综合结果较为吻合,表明基于云模型一风险矩阵法的自然灾害风险评价是可行有效的。文献[16]的评价方法存在一定的缺陷,例如当某个指标值很小时,评价结果会趋于较低的风险等级[17],而云模型充分考虑了评价指标风险分级边界的模糊性,因此基于云模型的评价结论更为合理。
5 结语
自然灾害风险评价受众多不确定性因素影响,本文把在定性与定量转化方面具有明显优势的云模型应用于自然灾害风险评价,不仅实现了自然灾害风险等级“极低风险”“低风险”“中等风险”“高风险”“极高风险”的定性描述,而且将其进一步转化为每个相应风险等级的定量数值,有效弥补了其他风险评价方法不能综合考虑评价指标随机性和模糊性等不确定性的缺陷,同时将风险矩阵理论应用于各风险指标评价结果的合成,比原有指标权重分配方法更能反映自然灾害风险形成机制。全国31个省级行政区的自然灾害风险评价结果表明,基于云模型和风险矩阵的自然灾害风险评价方法比其他方法的应用过程更为直观、简便,且结果可靠,具有一定的机理性,为综合处理风险评价过程中存在的模糊性与随机性问题提供了一种新思路。
参考文獻:
[l] 袁永博,窦玉丹,刘妍,等.基于组合权重模糊可变模型的旱涝灾害评价[J].系统工程理论与实践,2013,33( 10):2583-2589.
[2]
11 Y L,WANG T,SONC X Y, et al.Optimal Resource Al-location for Anti - Terrorism in Protecting Overpass BridgeBased on AHP Risk Assessment Model[J].KSCE Joumal ofCivil Engineering, 2016, 20(1):309-322.
[3] 王益伟,罗周全,杨彪,等,基于投影寻踪模型的矿山地下水灾害分级评价[J].中国安全生产科学技术,2014,10 (3):41-47.
[4]金菊良,魏一鸣,杨晓华,基于遗传算法的洪水灾情评估神经网络模型探讨[J].灾害学,1998,13(2):6-11.
[5] 陈亚宁,杨思全.自然灾害的灰色关联灾情评估模型及应用研究[J].地理科学进展,1999,18(2):158-162.
[6]CAIN A K, MOJTAHED V, BISCARO C,et al.An Inte-grated Approach of Flood Risk Assessment in the EasternPart of Dhaka City[ J]. Natural Hazards, 2015, 79(3):1499-1530.
[7]
DAHAL P,SHRESTHA N S,SHRESTHA M L,et al.DroughtRisk Assessment in Central Nepal:Temporal and Spatial Anal-ysis [J]. Natural Hazards, 2016, 80(3):1913-1932.
[8]李德毅,杜鹚,不确定性人工智能[M].2版,北京:国防工业出版社,2014:50-53.
[9]李健,汪明武,徐鹏,等.基于云模型的围岩稳定性分类[J].岩土工程学报,2014,36(1):83-87.
[10] 张秋文,章永志,钟鸣,基于云模型的水库诱发地震风险多级模糊综合评价[J].水利学报,2014,45(1):87-95.
[11] 邵莲芬,辛酉阳.基于投影寻踪一正态云模型的某土石坝安全评价[J].水电能源科学,2015,33( 12):81-84.
[12]
LIU Y C,MA Y T,ZHANC H S,et al.A Method for TrustManagement in Cloud Computing: Data Coloring by CloudWatermarking[J].Intemational Journal of Automation andComputing, 2011, 8(3): 280-285.
[13]
WANC S L,LID R, SHI W Z,et al.Cloud Model-BasedSpatial Data Mining[J].Geographic Information Sciences,2003.9( 1-2):60-70.
[14] 罗赟骞,夏靖波,陈天平,基于云模型和熵权的网络性能综合评估模型[J].重庆邮电大学学报(自然科学版),2009,21(6):771-775.
[15] 丁昊,王栋,基于云模型的水体富营养化程度评价方法[J].环境科学学报,2013,33(1):251-257.
[16]刘丽,代宏霞,中国自然灾害保险风险度综合评判与区划[J].山地学报,2004,22(4):477-482.
[17]王文圣,金菊良,李跃清,基于集对分析的自然灾害风险度综合评价研究[J].四川大学学报(工程科学版), 2009,41(6):6-12.
