基于正交试验的双内齿迷宫灌水器数值模拟
2019-09-10康苗业李治勤徐腾王泽
康苗业 李治勤 徐腾 王泽





摘要:在普通矩形迷宫流道灌水器的竖向流道与横向流道分别加入2个、1个内齿,构成4种内齿相对位置不同的双内齿矩形迷宫流道灌水器,并保持两者最小过流断面一致,以此探求加入内齿前、后迷宫流道灌水器水力性能的优劣,并采用数值模拟及正交试验的方法,选取内齿相对位置、内齿间距、内齿高度为主要因素,选取L16(45)正交表得到16组方案,通过方差分析与极差分析的方法,找到影响其水力性能的主要因素与次要因素,最终得到最优方案组合。结果表明:在普通矩形迷宫流道加入内齿后,其消能效果更好,流态指数减小11.18% - 18.01%;影响双内齿矩形迷宫流道的3个因素的主次顺序为内齿相对位置、内齿高度、内齿间距;双内齿矩形迷宫流道灌水器的流态指数最小的结构为竖向流道左上侧与右下侧、横向无涡处加入内齿,内齿间距0.5 mm,内齿高0.9 mm,其流态指数为0.500 6。
关键词:迷宫流道:数值模拟:正交试验;流态指数
中图分类号:S275.6
文献标志码:A
doi: 10.3969/j.issn. 1000- 1379.2019.06.036
迷宫流道灌水器是滴灌系统中的关键部件,其流道的水力性能直接决定滴灌系统的工作性能[1]。迷宫流道因为其自身结构的复杂性,具有良好的消能效果,因此被普遍认为是目前水力性能最好的灌水器流道结构之一。对迷宫流道灌水器的水力性能进行进一步的研究,不仅可为灌水器的发展提供基础理论依据,而且对进一步发展滴灌技术具有促进作用。影响滴头水力性能的主要因素是流道的结构形式,国内学者对流道结构参数与水力性能之间的关系进行了大量的研究。常莹华等[2]研究发现,迷宫流道的齿宽和齿底距均与流量、流态指数成正相关关系,且齿宽对流量和流态指数的影响较齿底距更为显著:郭霖等[3]采用均匀设计试验结合CFD软件模拟的方法,计算得到流量与流态指数,为建立流态指数和结构参数的数学关系提供了依据,得出三角形迷宫流道的最优流态指数:王芳等[4]利用FEMLEB软件对迷宫滴头进行三维的流道参数建模,结果表明水力性能与流道断面面积存在一定的相关关系,面积过小和过大均不适合水流的流态分析:王建东[5]选取7种典型迷宫流道形式进行正交试验,提出流道结构各因素对流态指数影响的大小顺序为齿间距>流道深度>齿角度>齿高:金龙等[6]研究了双内齿迷宫流道的最优水力性能结构组合,但并未考虑内齿相对位置对迷宫流道灌水器水力性能的影响。
本研究在普通矩形迷宫流道的基础上,在竖向流道及横向流道分别加入2个、1个内齿,形成4种内齿相对位置不同的双内齿矩形迷宫流道灌水器,并保持两者最小过流断面面积相等,采用正交试验方法设计试验,并通过Fluent数值模拟最终得到流态指数,对双内齿矩形迷宫流道灌水器的结构参数与流态指数的关系进行研究。
1 灌水器结构设计
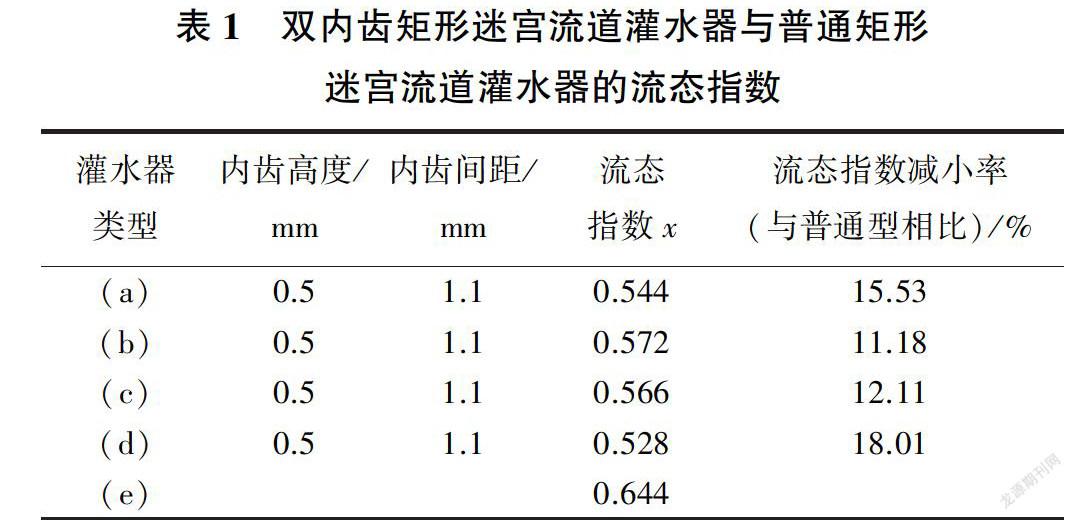
在普通矩形迷宫流道的基础上,在竖向流道及横向流道分别加入2个、1个内齿,并保持两者最小过流断面面积相等,形成4种内齿相对位置不同的双内齿矩形迷宫流道(见图1),图l(e)为普通矩形迷宫流道。结构参数包括流道高度H、流道宽度W、内齿高度h、内齿间距a、内齿宽度e。通过物理模型试验及幂函数拟合得到各个灌水器的流态指数(见表1),以此来比较其水力性能。
由表1可知,普通矩形迷宫流道的流态指数为0.644,而加入内齿的双内齿矩形迷宫流道的流态指数均小于0.6,最大为0.572,最小为0.528,较普通矩形迷宫流道减小11. 18% - 18.01%。在普通矩形迷宫流道中加入内齿后,流道边壁急剧变化,增加了对水流的阻力,消能效果显著,水力性能更加优越;内齿相对位置不同,其他结构参数相同时,各个双内齿矩形迷宫流道的流态指数差异显著,最小值比最大值减小7.69%,说明内齿相对位置也是影响灌水器水力性能的重要因素。本文采用数值模拟的方法计算出4种灌水器在不同结构参数下的流态指数,并通过正交试验、方差分析与极差分析,进一步研究影响灌水器水力性能的各种因素及其主次关系,旨在為迷宫流道的结构优化设计提供依据。
2 正交试验设计与数值模拟计算
2.1 正交试验设计
正交试验设计和分析方法是目前最常用的工艺优化试验设计和分析方法,是部分因子设计的主要方法[7]。正交试验是通过正交表合理地安排试验,利用数理统计原理分析试验结果,处理多因素试验的科学方法。其优点是通过代表性很强的少数试验,弄清各个因素对试验指标的影响,确定因素的主次顺序,找出较好的生产条件或最优参数组合。
本文采用正交试验在双内齿矩形迷宫流道灌水器的诸多试验条件中选出少数具有代表性的试验方案,通过对这些试验方案的结果分析,找出最优方案。正交试验设计如下。
(1)试验指标:灌水器的流态指数x。
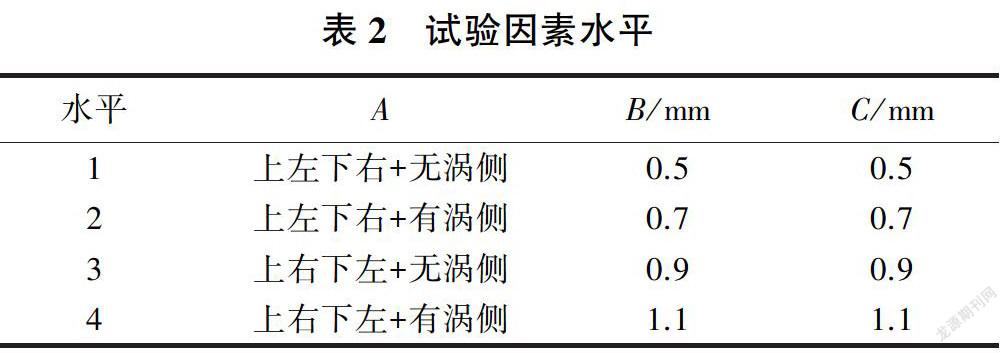
(2)试验因素:内齿相对位置A,内齿间距B,内齿高度C。
(3)试验因素水平的选取见表2。
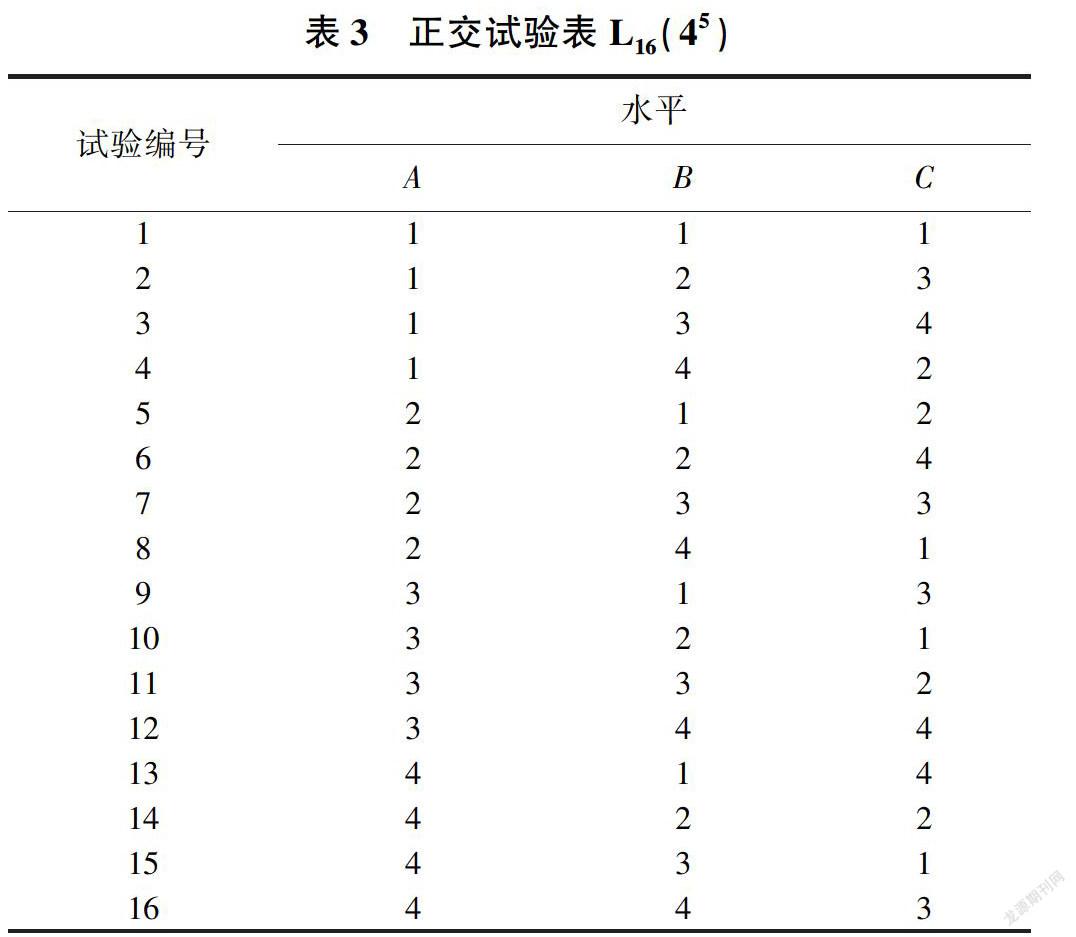
根据选定的试验因素和试验因素水平,设计正交试验表,见表3。
2.2 数值模拟计算
按照正交试验设计的结构尺寸,利用CAD与Gambit对灌水器进行1:1建模。由于迷宫流道灌水器的水力现象在单元上具有重复性,因此选取流道最后3个单元进行模拟[8]。迷宫流道灌水器内的流体可视为不可压缩的连续性流体,管道流动基本控制方程为连续性方程与N-S方程[9]。连续性方程为
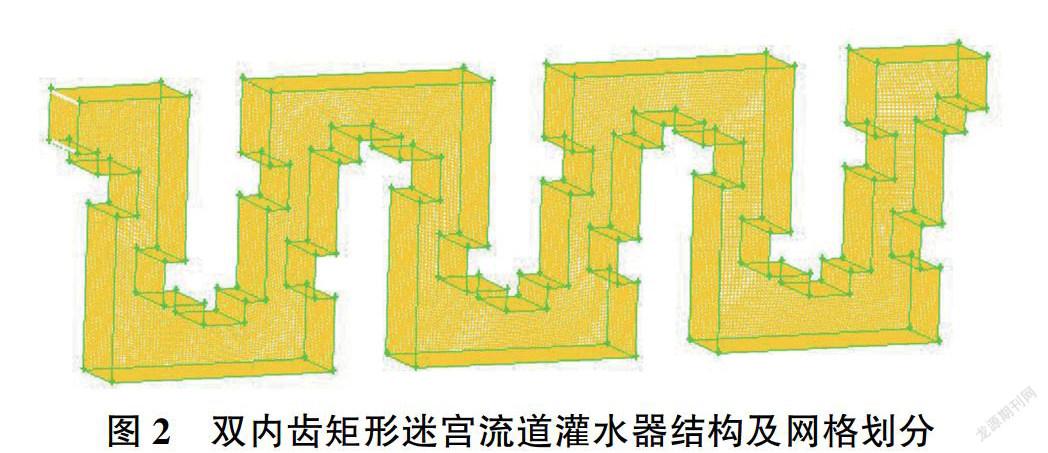
在CAD中绘制平面图导人GAMBIT,并构造三维模型,进行网格划分。通过物理模型试验与数值模拟的结果比较发现,在进行双内齿迷宫流道灌水器数值模拟时,上、下边界层第一层设置为0.01 mm,其他各层按1:2比例递增,设置5层,边界层总厚度为0.074mm[10]。采用Hex/Submap六面体网格、quad/map面网格(见图2).灌水器面网格与体网格网格间距均设置为0.08 mm,网格节点总数约为30万。该种网格划分形式的模拟计算结果与物理模型试验结果之间的误差较小,且易收敛,在后续的不同结构参数的网格划分中全部采用这种形式。
灌水器的进口与出口边界条件设置为压力进口与压力出口,进口压力水头控制为5-15 m,出口压力为0(以一个标准大气压为基准)。模型采用有机玻璃制作,根据厂家建议,壁面粗糙度取0.01 mm.对壁面采用默认标准壁面函数法进行处理。流场数值计算采用压力一速度耦合式SIMPLE解法,压力项等采用一阶迎风格式。进行迭代计算时,收敛残差取10-3。3结果分析
当压力水头在一定范围时,灌水器压力与流量的关系可表示为
g= kH
(5)式中:g为灌水器的流量,L/h;H为灌水器的工作压力水头,m;x为流态指数(0≤x≤1),表示流量对压力的敏感程度,当x=0时表示流量不会随着压力的变化而变化,当x=l时表示流量与压力成线性关系:为流量系数。
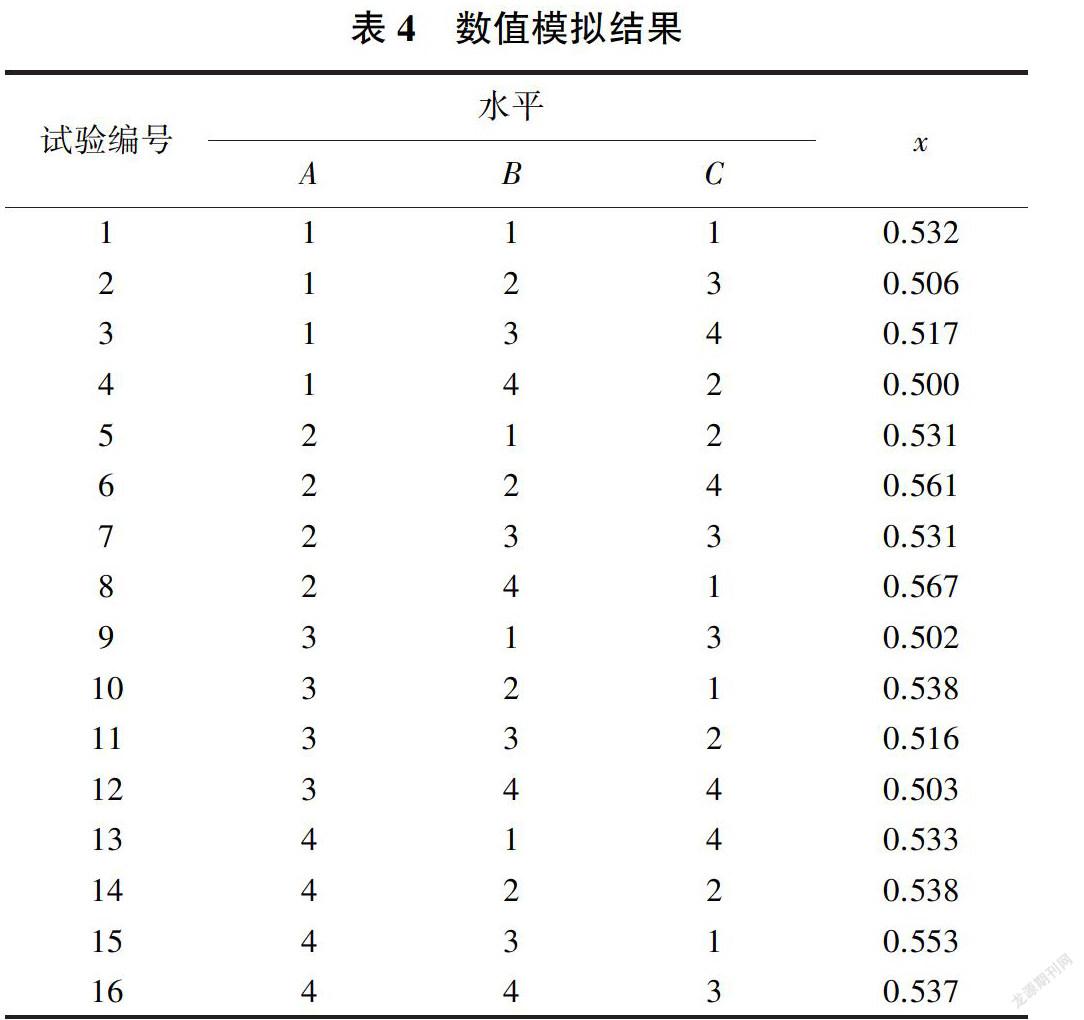
将进口压力水头控制为5-15 m,通过每次模拟计算可以得到其流速,进而计算其流量。根据式(5),采用幂函数对数值模拟所得的压力与流量进行拟合,得到所需的流态指数,见表4。
由表4可以看出,不同水平组合下的流道结构,其流态指数相差较大,范围为0.500 - 0.567,最小流态指数比最大流态指数减小11. 82%,说明内齿相对位置、内齿高度、内齿间距对灌水器水力性能均有影响。采用方差分析与极差分析可以得到影响双内齿矩形迷宫流道水力性能的主要因素及其主次顺序,从而可以得到最优流道结构。
3.1 方差分析
方差分析可以把改变因素水平所引起的试验结果的波动与试验误差所引起的试验结果的波动区分开来,能够提供判断因素对试验结果的影响是否显著的标准。采用SPSS软件选定相应的变量参数进行方差分析,结果见表5。
按显著性水平α=0. 05来检验时,内齿相对位置与内齿高度对流态指数x影响显著,内齿间距对流态指数x影响不显著。金龙等[6]提出,流态指数随着内齿高度的增大呈现先增大后减小的趋势,内齿间距对流态指数与流量系数基本无影响,验证了本研究结果。在以后的研究中,可以着重研究内齿相对位置与内齿高度对其水力性能的影响,但是需要知道影响水力性能的主要因素与次要因素,以便对灌水器结构进行优化,可以采用极差分析法来实现。
3.2 极差分析
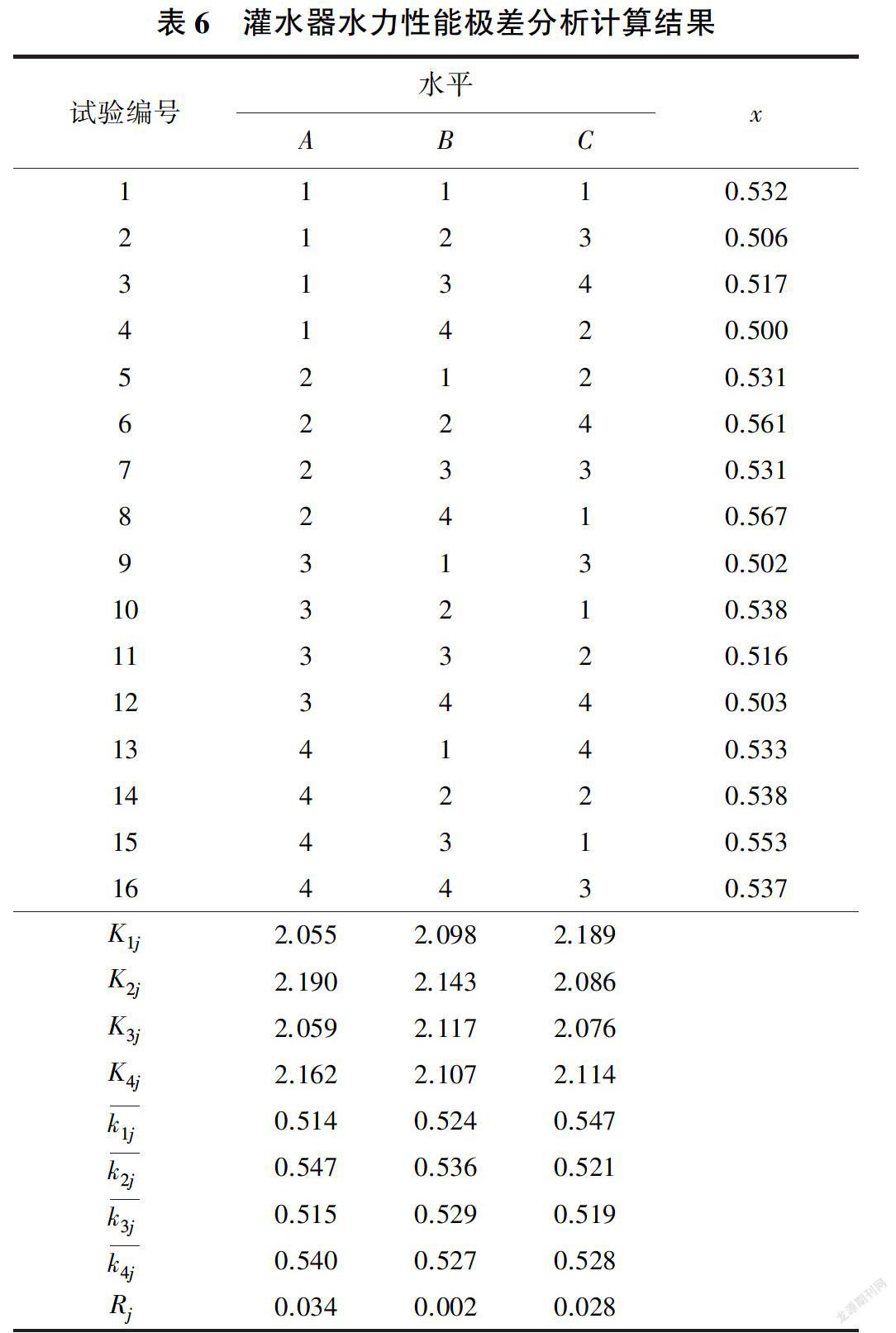
Rj越大,说明该因素的变化水平对试验指标的影响越大,即该因素越重要。由表6可知,影响双内齿矩形迷宫流道水力性能的因素主次顺序为内齿相对位置、内齿高度、内齿间距。
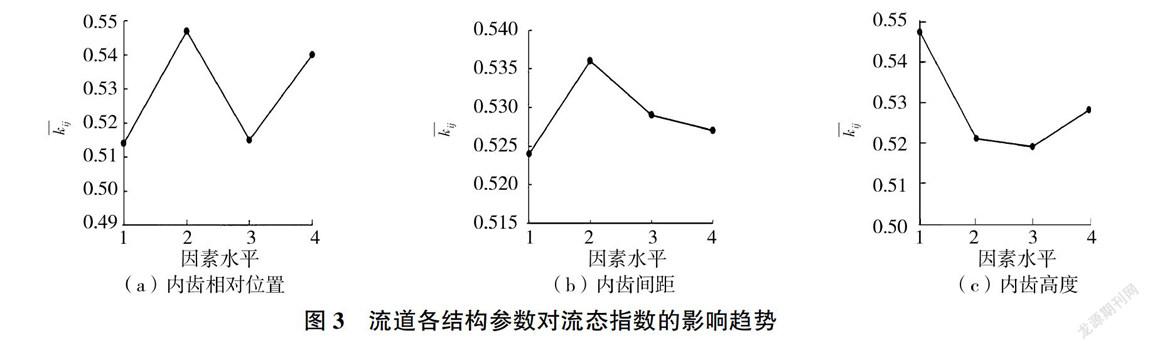
由表6中各因素不同水平下的平均值,可以看出各因素的水平变化时指标(流态指数)的变化趋势。将各因素在不同水平下的流态指数均值用因素水平一指标关系图来表示,即以因素水平为横坐标,各因素不同水平下的平均值k为纵坐标来作图[12-13],以此来探求每个因素下的最优水平,见图3。
由图3可知,当内齿相对位置为竖向流道左上侧与右下侧、横向流道无涡处加齿、内齿间距为0.5 mm、内齿高度为0.9 mm时,流道结构最优,其对应的因素水平组合为A1B2C3。此组合方案在正交表中没有出现,通过数值模拟方法计算该组合下的流态指数为0.500 6,说明该结构下灌水器的水力性能优越,在以后的双内齿矩形迷宫灌水器的流道结构设计中,可以参考该结论进行设计。
4 结论
(1)在普通矩形迷宫流道灌水器的竖向流道与横向流道分别加入2个、1个内齿,并保持最小过流断面不变,形成4种内齿相对位置不同的双内齿矩形迷宫流道灌水器,试验结果表明双内齿矩形迷宫流道灌水器的水力性能均优于普通矩形迷宫灌水器,流态指数减小11. 18% - 18.01%。
(2)利用正交试验的方法分析内齿相对位置、内齿高度、内齿间距3个因素对双内齿矩形迷宫流道灌水器水力性能的影响程度,结果表明各水平组合下的流态指数相差较大,最小流态指数比最大流态指数减小11 .82%,说明这三个因素均对双内齿矩形迷宫流道的水力性能有影响。
(3)方差分析结果表明,按显著性水平α=0.05来检验时,内齿相对位置与内齿高度对流态指数x影响显著,内齿间距对流态指数x影响不显著。
(4)极差分析结果表明,内齿相对位置对双内齿矩形迷宫流道灌水器的水力性能影响最大,其次为内齿高度,内齿间距影响最小。
(5)双内齿矩形迷宫流道灌水器的最优水平组合为AiBi C3,即灌水器的结构为:在竖向流道的左上侧与右下侧、横向流道的无涡处加入内齿,内齿间距为0.5 mm,内齿高度為0.9 mm,其流态指数为0.500 6。
参考文献:
[l] 王晓虹,灌水器迷宫流道结构设计与水力性能试验研究[D].西安:西安理工大学,2006: 1-10.
[2] 常莹华,牛文全,王维娟.滴灌灌水器迷宫流道的内部流体数值模拟与流动分析[J].西北农林科技大学学报(自然科学版),2009,37(2):203-208.
[3]郭霖,白丹,程鹏,等,滴灌灌水器三角形迷宫流道优化设计[J].排灌机械工程学报,2015,33(7):634-639.
[4] 王芳,吴普特,范兴科,滴灌灌水器迷宫流道数值模拟与结构优化设计[J].灌溉排水学报,2007,26(3):35-37.
[5] 王建东.滴头水力性能与抗堵塞性能试验研究[D].北京:中国农业大学,2004:20-28.
[6] 金龙,李治勤,马彦超,等.双内齿矩形迷宫流道灌水器水力特性分析[J].太原理工大学学报,2016,47(6):774-778.
[7] 刘瑞江,张业旺,闻崇炜,等.正交试验设计和分析方法研究[J].试验技术与理论,2010(9):52-55.
[8] 魏正英,唐一平,赵万华,等.滴灌灌水器迷宫流道结构与水力性能试验研究[J].农业工程学报,2005,36( 12):51-55.
[9] 王福军,计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004: 111-123.
[10] 李云开,杨培岭,吴显斌,等.重力滴灌灌水器水力性能及其流道内流体流动机理[J].农业机械学报,2005,10( 36):54-57.
[11]朱勇华,部淑彩,孙锡玉.应用数理统计[M].武汉:武汉水利电力大学出版社,1998:210-260.
[12] 袁建平,李淑娟,付跃登.用正交试验研究分流叶片对离心泵性能的影响[J].排灌机械,2009,27(5):306-309.
[13] 张俊,洪军,赵万华,等,基于正交试验的迷宫流道灌水器参数化设计研究[J].西安交通大学学报,2006,40 (1):31-35.
