移动荷载作用下简支梁振动减振分析

马信欣 袁波 尹浩熹 何海玉 郑勇

摘 要：振动控制是解决大跨轻质人行天桥舒适度的关键问题之一。通常会采用调谐质量阻尼器（TMD）进行减振，可以有效降低桥梁在行人激励下的振动反应。将行人激励简化为移动简谐荷载，建立人群-人行桥-TMD振动系统，推导在匀速移动人行荷载下，人群-人行桥-TMD振动系统的运动微分方程。并结合某一人行天桥实例，对该人行天桥进行添加TMD后的Simulink仿真分析，与Ansys建模分析的结果进行对比，说明Simulink仿真分析的正确性。采用中国规范进行舒适度分析，选取一定范围人行荷载的频率，并用Simulink对此简支梁桥进行定质量TMD与变质量TMD的减振分析，分析结果表明变质量TMD减振效果优于定质量TMD减振效果。

关键词：SIMULINK仿真系统;变质量动力吸振器;振动控制;人行桥;TMD

中图分类号：U441+.3

文献标识码： A

随着我国的经济增长和城市交通的不断建设，人行桥也正向大跨度轻柔低阻尼的方向发展，人们对人行桥的舒适度要求更加严格，对大跨度人行天桥施加多人行走的人行荷载，如果荷载频率与桥梁的自振频率相同时，就会发生共振，则桥梁的响应将被不断增大，轻则会使人心理上产生不舒适感，严重时会使桥梁发生破坏[1-2]，本文研究多人同频率匀速通过桥梁时的最大动力响应，并对桥梁添加TMD[3-6]阻尼器进行减振控制，因常用的有限元软件建模分析时间较长，采用较高效的Simulink软件进行减振分析，首先推导人群-桥-TMD的动力方程，然后在Simulink中依据运动方程建立仿真模块，进行动力仿真分析。得出桥梁挠度最大点在仿真分析与有限元软件分析下的加速度与位移时程曲线，并对两种软件的结果进行对比，证明仿真的准确性。运用变质量TMD[7]，并对定质量TMD与变质量TMD进行仿真对比分析并得出结论。

1 运动方程的建立

1.1 结构分析模型

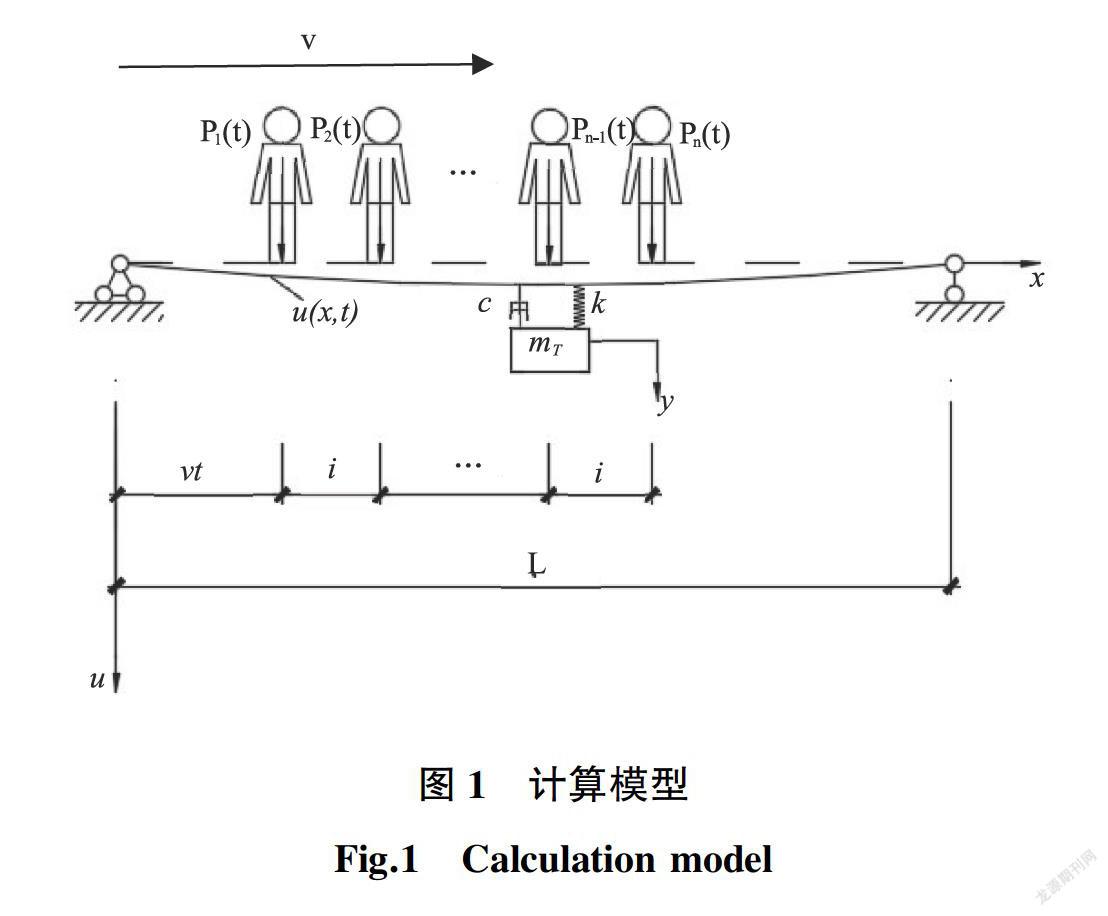
本文分析的结构模型如图1所示，人行荷载简化为一移动简谐荷载，n个等间距的行人以速度v陆续从左至右通过长度为L的简支梁桥，主梁为等截面均匀简支梁，抗弯刚度为EI，单位长度质量为m，在桥梁中间布置TMD阻尼器，c、k分别为TMD阻尼和刚度，y以静平衡位置为原点，u（v，t）为桥梁挠度，在TMD下的初始挠度u（0）忽略不计。

1.2 运动方程建立

在匀速移动简谐荷载作用下的简支梁及定质量TMD[8-10]系统的运动方程分别为：

m2u（x，t）t2+EI4u（x，t）x4+csu（x，t）t+mTy¨δ（x-l/2）=∑ni=0δ（x+i-vt）Pi（t）（1）

mTy¨+c（y·-u·|l2）+k（y·-u·|l2）=0（2）

式中，m单位长度质量;EI为截面抗弯刚度;U（x，t）为距梁端点x、时间t时的竖向挠度;g为重力加速度;δ为Dirac函数;P（t）为简化的人行荷载;cs为阻尼系数;c为TMD阻尼;k为TMD刚度;mT为TMD的质量

将式（2）导入式（1）中得下式（3）

m2u（x，t）t2+EI4u（x，t）x4+csu（x，t）t-k（y-ul2）+c（y·-u·l2）δ（x-l/2）=∑ni=0δ（x+i-vt）Pi（t）（3）

利用分離变量法，令

u（x，t）=∑SymboleB@

n=1φn（x）qn（t）（4）

式中，φn（x）=sinnπlx（n=1，2，…）为振动的形状，不随时间变化;qn（t）为随时间变化的振幅

将式（4）代入式（3），可得下式（5）：

m∑SymboleB@

n=12qn（x，t）t2φn（x）+EI∑SymboleB@

n=14φn（x）x4qn（t）+cs∑SymboleB@

n=1qn（x，t）tφn（x）-k（y-ul2）+c（y·-u·l2）

δ（x-l/2）=∑ni=0δ（x+i-vt）Pi（t）（5）

由式（5）两边同时乘上φn（x），再（0，l）内积分，利用振型正交性可得式（6）

Mnq¨n（t）+2ξnωnMnq·n（t）+ω2nMnqn（t）-

φn（l/2）k（y-ul2）+c（y·-u·l2）=Pn（t）（6）

式中第n阶频率ωn、振型质量Mn、振型力Pn（t）、振型阻尼比ξn表达式如下，令ξ1=ξ2=0.02：

ωn=n2π2l2EIm;Mn=∫l0[φn（x）]2mdx=mL/2;

Pn（t）=∑ni=0∫l0φn（x）δ（x-i-vt）Pi（t）dx

=∑ni=0φn（vt-i）Pi（t）

a=2ω1ω2（ξ1ω2-ξ2ω1）ω22-ω21

=0.032π2l2EIm;

b=2（ξ2ω2-ξ1ω1）ω22-ω21

=0.08l2π2mEI;

ξn=a2ωj+bωj2=0.016j2+0.04j2

背户一登在文献[11]确定的动力吸振器的最佳阻尼条件和最佳调谐条件由式（7）和式（8）确定。

ζopt=3μ8（1+μ）3（7）

λopt=11+μ（8）

其中，质量比μ=mT/M， mT为TMD质量，M是结构模态质量，μ取1%-5%。根据ω2=k/mT经过数学推导得出最优阻尼比Copt与最优刚度比kopt，如式（9）与式（10）示。

copt=2ζoptλoptωmT（9）

kopt=λopt2ω2mT（10）

振型力Pn（t）矩阵形式如下：

P=∑ni=0φ1（vt-i）Pi（t）∑ni=0φ2（vt-i）Pi（t）∑ni=0φn（vt-i）Pi（t）0

TMD的振动方程为：

mTy¨+cy·+ky-c∑SymboleB@

n=1φnl2q·n（t）-

k∑SymboleB@

n=1φnl2qn（t）=0（11）

为了进行矩阵求解，将所有振型的运动方程联合上式的TMD振动方程，统一写为

MX¨（t）+CX·（t）+KX（t）=P（12）

式中，模态质量M、刚度矩阵K与阻尼矩阵C如下所示，根据文献[5]可知，f1≥1.4 Hz的简支人行桥，仅取第一阶模态即可准确计算出跨中加速度的动力反应。

M=M1MnmT

C=2ξ1ω1M1+∑nicφ21l2…∑nicφ1l2φ2l2-φ1l2c对称2ξnωnMn+cφ2nl2-φnl2cc

K=ω21M1+∑nikφ21l2…∑nikφ1l2φ2l2-φ1l2k

ω2nMn+kφ2nl2-φnl2kk

2 Simulink动态仿真设计

进行Simulink仿真，首先在matlab[12]中输入初始参数，计算桥梁固有频率与阻尼比，然后在

Simulink建模窗口中建模，并进行各模块参数的设置，其次仿真调试阶段，检查模块连接。最后进行仿真设置，并运行仿真;输出运算结果到workspace。根据式（12）的动力微分方程在Simulink中建立模块，并进行动态仿真分析[13]。仿真框图见图2。

3 Ansys结果对比分析

3.1  算例

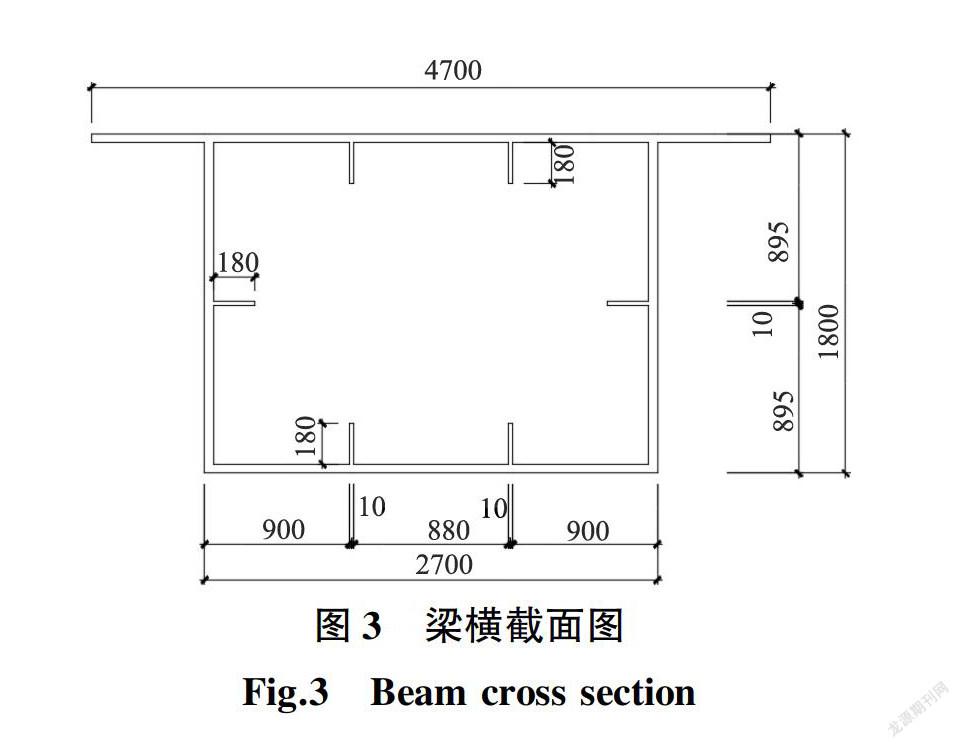
为了验证上述理论分析的正确性，引用文献[14]中的算例，该人行天桥的人流量在30人/分钟左右，可以计算出同时在桥上的人数为17人，17人以匀速v从左向右陆续通过该人行天桥。此桥梁的基频f1为2.5625 rad/s，人行荷载频率同基频f1。主梁为等截面均匀简支梁，图3为梁横截面图，主梁采用单箱单室钢箱梁，梁高为1.8米，腹板厚25毫米，顶板宽度4.7米，底板宽2.7米。抗弯刚度为EI，单位长度质量为m，结构的基本参数见表1。

3.2 Ansys结果对比

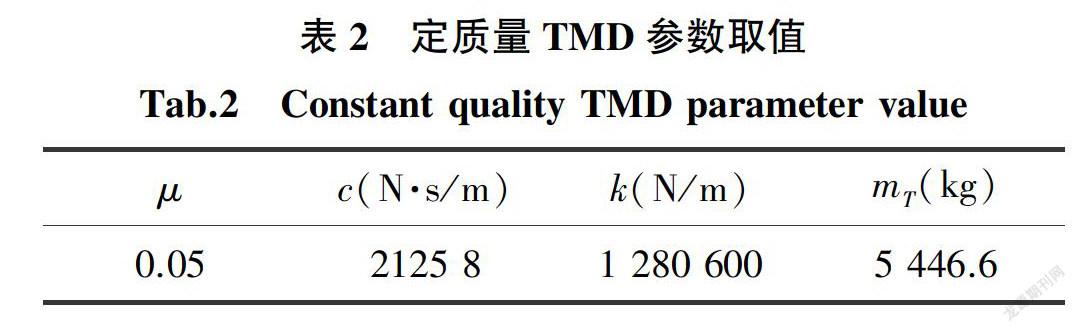
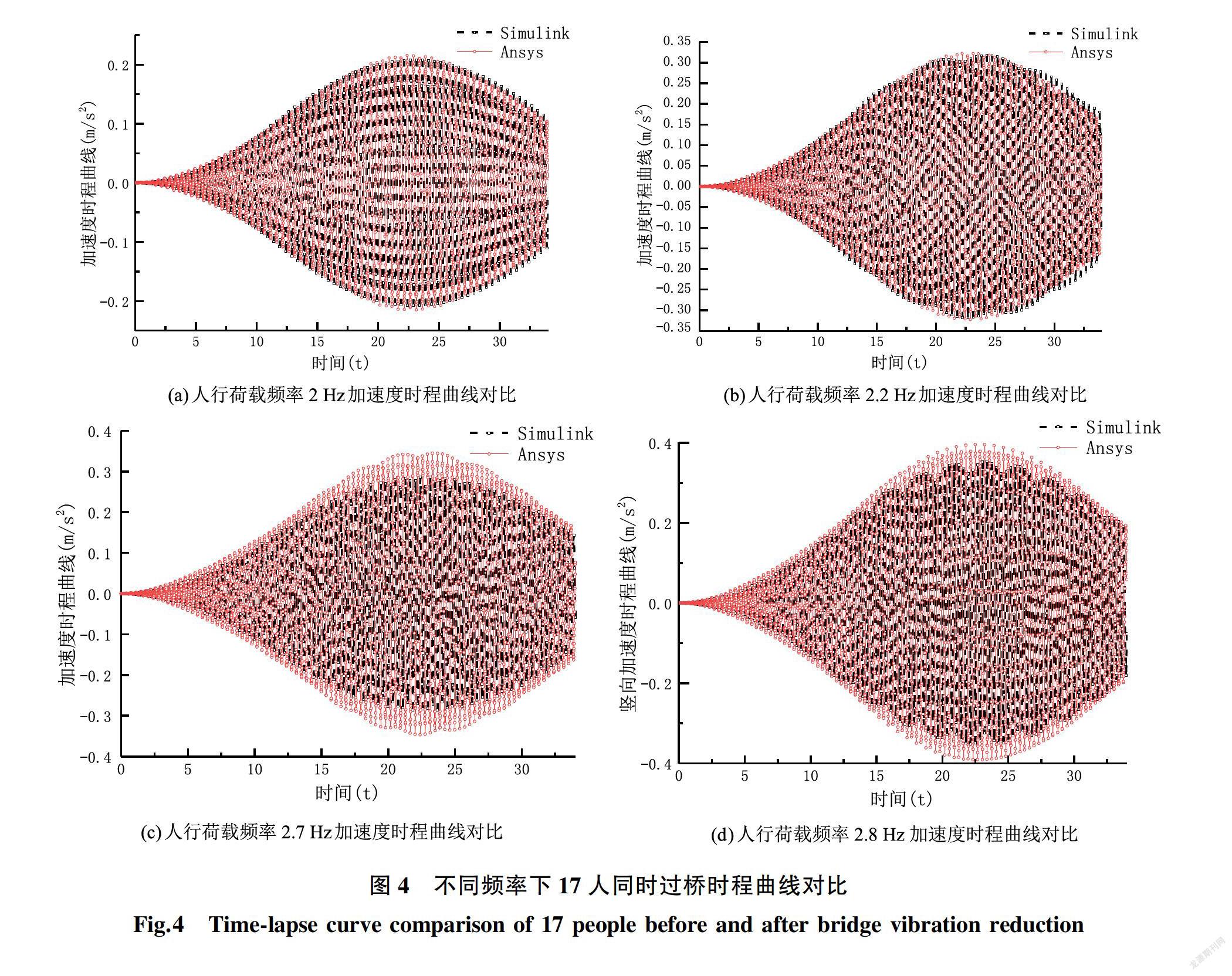
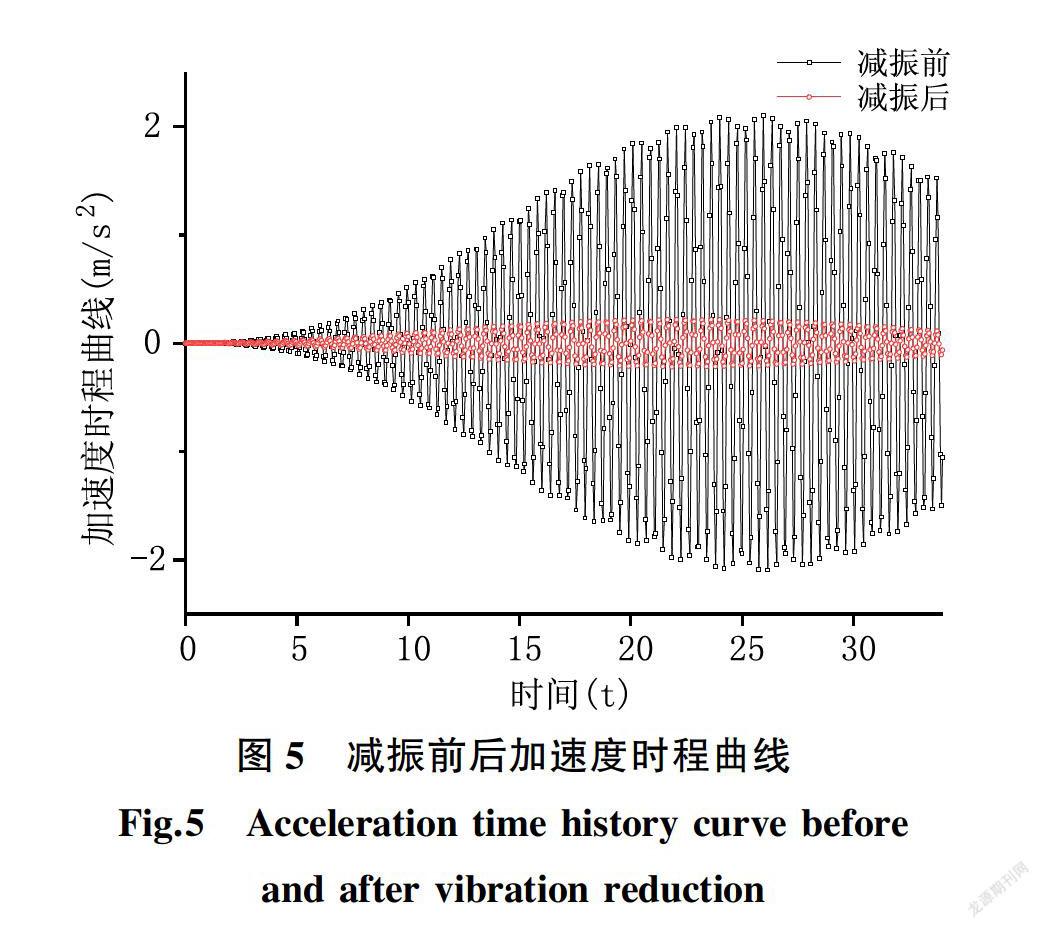
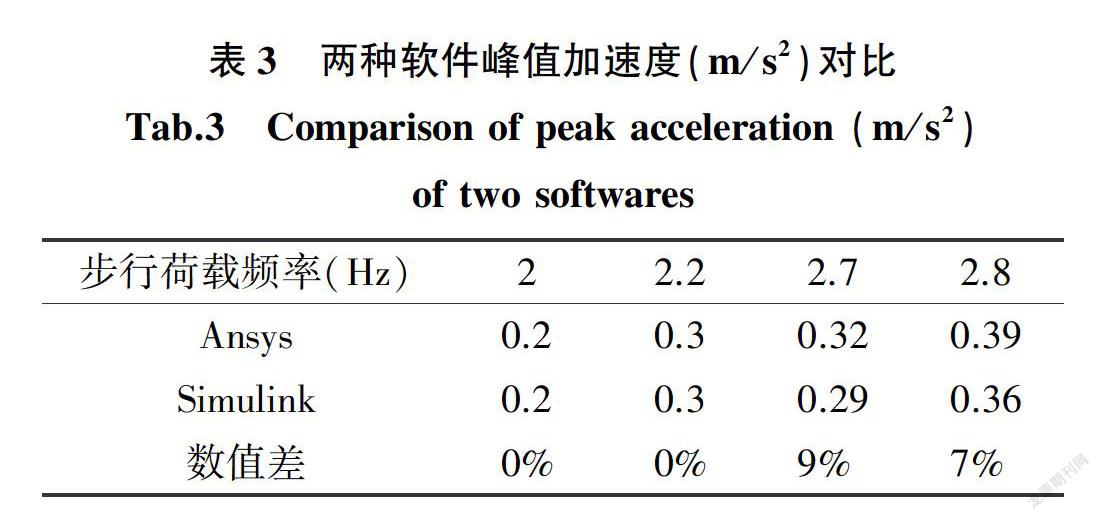
分析在正常步行荷载频率2 Hz～3 Hz范围内，上述算例中定质量TMD的参数根据公式（7）-（10）进行计算，得出定质量TMD的参数取值如下表2所示。17人列队过桥时Simulink与Ansys分析的加速度时程曲线的对比如图4与表3所示。从图4与表3可知，两种软件分析结果差值小于9%，故结构仿真正确。当行人与桥梁共振时，桥梁

振动响应最大，采用质量比为0.05的TMD进行减振，减振前后时程曲线如图5所示，此时Simulink减振后峰值加速度为0.28 m/s2小于0.8 m/s2，减振效果为87.27%，满足规范[15]要求。

4 变质量TMD与定质量TMD对比分析

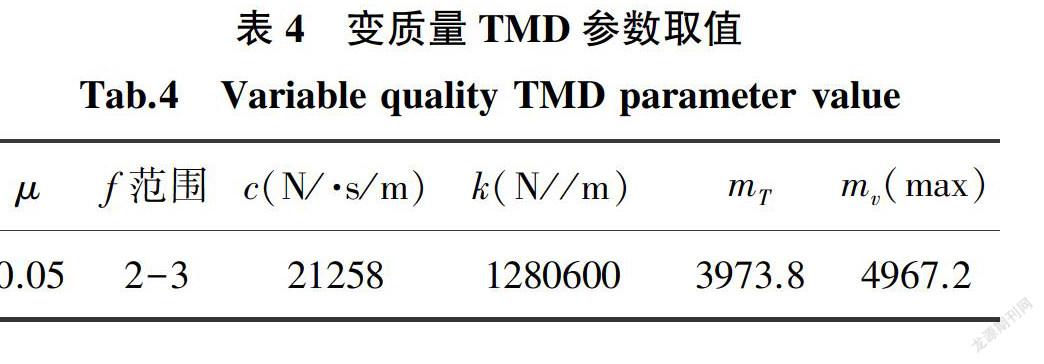
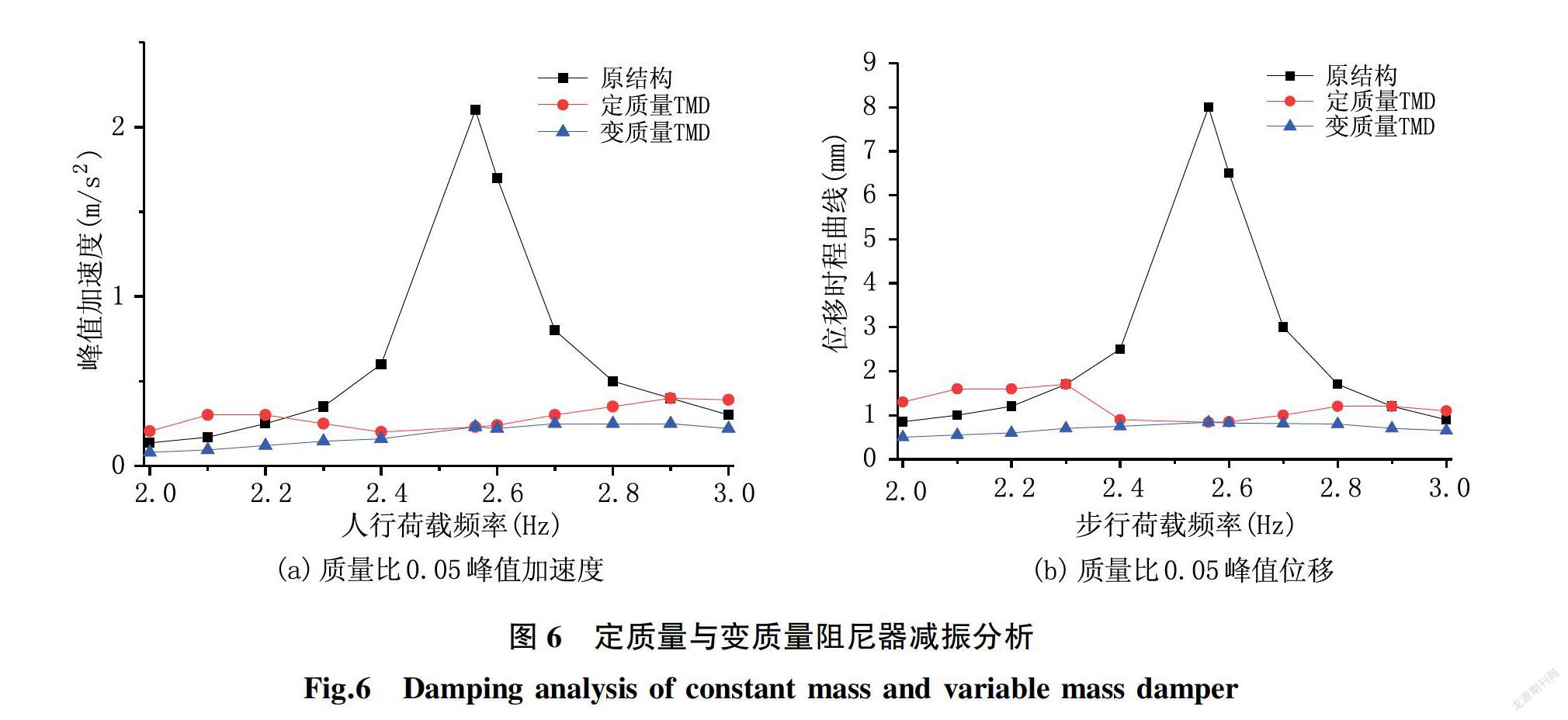
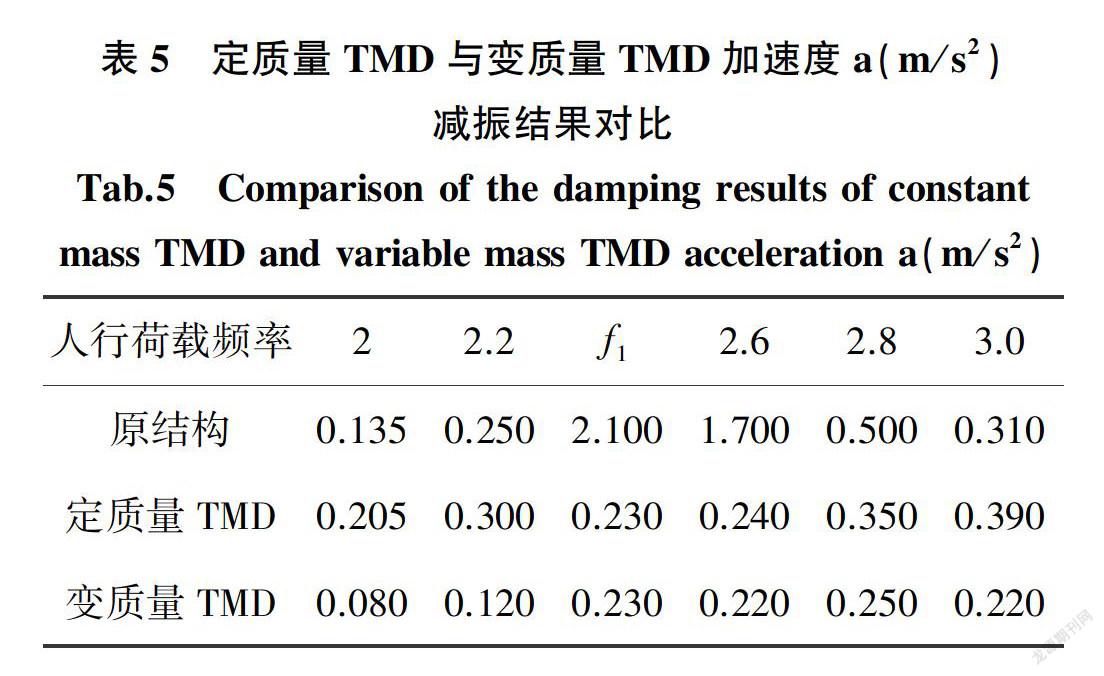
人的步行频率不是一个固定值，步行荷载频率一般在2～3 Hz频率范围内，定质量TMD只对某一频率减振效果明显，而变质量TMD能够根据步行荷载频率变化而调节吸振器质量来进行减振，其减振频率范围较宽。为了分析变质量TMD与定质量TMD的减振效果，同样采用3.1中的算例。变质量TMD的阻尼与刚度与3.2中定质量TMD参数相同，变质量TMD的定质量部分mT的取值根据公式mT=k/（λopt2πf（max））2确定。变质量TMD的变质量块mV的最大值根据公式mV（max）= k/（λopt2πf（min））2-mT，变质量TMD的参数如表4所示，Simulink的分析结果如图6所示。

5 结论

（1）本文推导了人群-人行桥-TMD的运动方程，根据运动方程建立了Simulink仿真框图，并对简支梁桥进行了动力仿真分析，仿真结果与Ansys建模分析结果进行对比。当17人匀速同频率通过桥梁时，两种程序对不同人行荷载频率的减振结果表明，峰值加速度最大相差9%，證明Simulink仿真方法的准确性。

（2）变质量TMD减振效果要优于定质量TMD减振效果，定质量TMD只对2.2～2.9 Hz范围内的步行频率进行减振，而变质量TMD对正常步行频率范围内都有减振效果。

参考文献：

[1]李慧乐，夏禾，郭薇薇.移动荷载作用下简支梁共振与消振机理研究[J].工程力学，2013，30（07）：47-54.

[2]武文涛. 基于人群—桥梁耦合振动理论的人行悬索桥振动研究及参数分析[D].西南交通大学，2016.

[3]李宏男，李忠献，等.结构振动与控制[M].北京：中国建筑工业出版社，2005.2018-237

[4]丁文镜.减振理论 [M].北京：清华大学出版社，1998

[5]樊健生，陈宇，聂建国.人行桥的TMD减振优化设计研究[J].工程力学，2012，29（09）：133-140+156.

[6]李上伟. 行人荷载下大跨钢箱梁人行桥动力响应分析与TMD减振控制[D].广州大学，2016.

[7]房祥波. 变质量动力吸振器及其控制策略研究[D].长安大学，2013.

[8]张军. 多个移动常量力作用下简支梁的动力仿真技术[A].2008：3.

[9]许磊平，刘伟庆，徐秀丽，王曙光，李勇智.TMD抑制桥梁振动仿真分析[J].防灾减灾工程报，2009，29（03）：272-276.

[10]张璨. 重载列车振动对桥梁的影响及减振控制[D].武汉理工大学，2017.

[11]背戶一登.结构振动控制[M].机械工业出版社，2010

[12]宋兆基，徐流美.MATLAB6.5在科学计算中的应用[M].北京：清华大学出版社，2005

[13]黎明安.MATLAB/Simulink动力学系统建模与仿真[M].国防工业出版社，2012

[14]伍定一. TMD对钢结构人行天桥的振动控制研究[D].长沙理工大学，2007.

[15]城市人行天桥与人行地道技术规范（征求意稿） ：CJJ69—201X[S].

（责任编辑：江 龙）

Vibration Reduction Analysis of Simply Supported

Beam Under Moving Load

MA Xinxin， YUAN Bo*， YIN Haoxi， HE Haiyu， ZHENG Yong

（Space Structures Research Center of Guizhou University ，Guiyang 550025）

Abstract：

Vibration control is one of the key issues to solve the comfort of a large span lightweight pedestrian bridge. The tempered mass damper （TMD） is usually used for vibration reduction， which can effectively reduce the vibration response of the bridge under pedestrian excitation. The pedestrian excitation is simplified to the mobile harmonic load， and the crowd￣footbridge￣TMD vibration system was established. The differential equations and state equations of the crowd￣footbridge￣TMD vibration system under the uniform moving pedestrian load were derived. Combined with a pedestrian bridge instance， the Simulink simulation analysis of the pedestrian bridge after adding TMD was compared with the results of Ansys modeling analysis. The accuracy of Simulink simulation analysis was illustrated. The Chinese standard was used for comfort analysis， the frequency of a certain range of pedestrian loads is selected， and the vibration reduction analysis of the traditional TMD and the variable mass TMD was carried out on the simply supported beam bridge by Simulink. The analysis results show that the variable mass TMD damping effect is better than the traditional TMD vibration reduction effect.

Key words：

SIMULINK simulation system; variable mass dynamic vibration absorber; vibration control;footbridge;TMD