巧用变式练习，巩固强化新知

张兆富 卢统新

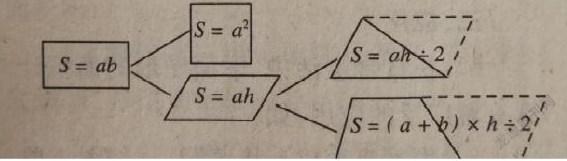
【摘要】新课之后有目的、有序有趣、有层次、有梯度而且实用的变式练习，不但不会使学生厌烦，造成负担，反而会让学生积极性提高，激发学习数学兴趣，让模糊问题变得更加清晰，疑难问题豁然开朗，并能体会一题多解的巧妙算法，获得更多的成功喜悦。

【关键词】变式练习;强化新知;层次性;灵活性;主体性;指导性;遵循规律

学生学习的数学学习内容应当是现实的，有趣的，富有挑战性的。传统的教学中，老师常常在一定程度上存在着“以课堂为中心，以教师为中心和以课本为中心”的倾向。这种单一、被动的学习方式往往使学生感到枯燥、乏味、负担重。数学来自于生活，又必须回归于生活。数学是让学生学会解决生活中的实际问题，使学生感到解决数学问题是一种有意义的活动。新课之后，教师如果精心设计变式练习，可以让学生有一种“山穷水尽疑无路，柳暗花明又一村”的喜悦，能帮助学生真正理解和掌握基本的数学知识和学习方法，有效地开发学生的潜能，发展学生的创新精神。

一、变式练习要有鲜明的层次性

教学乘法的初步认识，学生通过学习，已经知道乘法是相同加数连加的简便运算，掌握了乘法算式的读法和写法，知道了乘法算式的各部分名称。为了巩固乘法的意义，笔者采用变式练习。

1.判断哪组算式可以用乘法计算？

2+3+4 3+3+3+3

4+7+6 8+8+8

5+4+3+2 6+6+6

5+5+5+5 10+10+10

2.改写成加法算式

5x4=9x2=4x3=6x5=1x4=7x4=

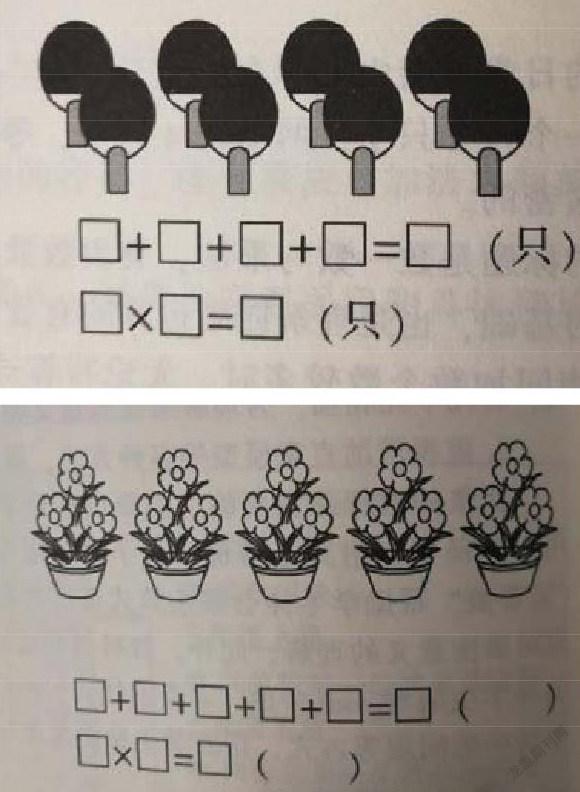
3.看图填空

4.每个学习小组有4个同学，全班分成了10个学习小组，全班一共有多少人？

算式：

5.小红、小明和4个小朋友去公园玩，门票每人5元，他们买门票一共要多少元？

算式：

6.求几个的和，用计算比较简便

学生已经初步认识乘法后，我围绕乘法的意义，设计有层次的变式练习，用判断、改写、图式对应，加乘对应，逐步到解决问题。学生既巩固了新知，又真正达到了学以致用的目的。

二、变式练习突出灵活性

教学能被3整除的数的特征，学生通过探究、讨论、验证等方法，已经掌握了能被3整除的数的特征。笔者设计了灵活的变式练习。

1.手势判断：下面哪些数能被3整除？

630 3054 16 216 123 1234

2007 358 113 5910

2.在方格里填上合适的数字，使原数能被3整除。（你能想出几种填法？）

O4，O93，O021，6O3

3.改变一个数字，使它能被3整除

473：O734O347O

4.判断下面哪些数能被3整除。（抢答）

9939、1369、30069、2369、3425

教学中通过练习，使学生理解能被3整除的数的特征，利用掌握的特征去判断、推理、分析。通过改变一个数字，使它能被3整除，让学生充分调动积极性，突破只看数“加”的思维定势，激发大脑“活”起来，既要学生“加”数，又要学生“找”数，让学生发现规律，找到规律。变式练习的精心设计，体现了教师为主导、学生为主体的教学原则，突出了练习的灵活性。

三、变式练习突出学习的主体性

教学面积的复习课，笔者设计的复习内容是先让学生梳理知识，然后灵活运用面积公式解决问题。

1.谁会写出面积的计算公式？

首先让学生板演，然后老师出示：

学生通过整理后，老师出示的图让学生一目了然，面积公式外加上图形，起到了“画龙点睛”的效果。

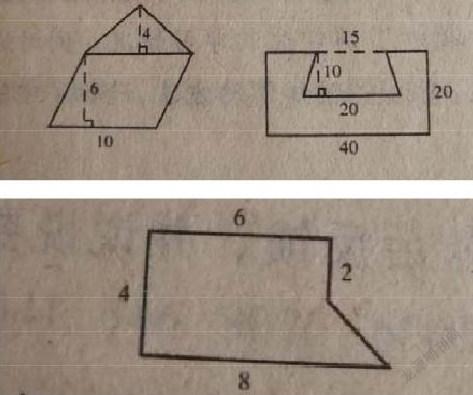
2.计算下面各图形的面积

图1、图2笔者让学生独立计算后反馈，说说你是怎么想的？然后老师总结：分割求和法和添补求差法是计算组合图形面积的两种最基本的方法。

图3，笔者启发学生：能用几种方法就用几种方法，可以小组讨论。

方法一：

6×2+（6+8）×2÷2

方法二：

（2+4）×6÷2+8×2÷2

方法三：

6×4+2×2÷2

方法四：

（6+8）×4÷2-2×2÷2

方法五：

8×4-（2+4）×2÷2

3.一塊长方形空地，植树节进行了绿化。（如图，单位：米）求草坪的面积是多少？

4.一块菜园，（如图，单位：米）篱笆全长36米，这块菜园面积是多少？

教学中让学生写一写，分一分、拼一拼，重视学生思维能力的培养，打破求平面图形面积一般方法的定势，巧妙变式练习，让学生“跳一跳”才能摘到果实的方法，让学生真正成为学习的主人，让课堂焕发活力，知识得到巩固。

最后老师总结，表扬作对的学生。让学生自主探究，独立或小组通过讨论合作，想办法解决。启发学生用多种方法解答，这样丰富了学生的解题策略。

四、变式练习突出教师的主导性原则。

教师只是学习活动的组织者，只是为学生提供环境、条件、情境刺激的创造者，同时是一个积极的鼓动者和参与者。教师在课堂教学中成为学生中的“一个”，参与学生的共同活动，而不是自作权威，高高在上，成为机械传递知识的简单工具，只有这样，教师才能把准学生的学习方向，进入学生的内心，和学生的情感产生共鸣、撞击和生发，才能有“天光云影共徘徊”的教学效果。学生觉得难，老师也要认同是有点难，引导学生找到合适的方法去突破“难”点，学生才会豁然开朗，才会起到“一石激起千层浪”，到达引人入胜的美景。

教学完圆柱的体积，学生知道了圆柱的体积公式，还知道和圆柱等底等高的圆锥体积是圆柱体积三分之一。教师复习时，让学生分成8个小组自己出题：填空、判断、选择、应用题各出2题（即每个小组抽签出一题），通过评分比赛。老师展示每个小组出的题，其他同学都参与完成，集体订正。学生学习的积极性很高，课堂气氛相当活跃，都想挑战一下别组出的题呢。题目展示如下：

第1、2小组填空：

1.在一个棱长1dm的正方体里截出一个最大的圆柱，圆柱的体积为（  ）cm3

2.一个正方体铁块边长是4cm，把正方体铁块铸成一个最大的圆柱体，圆柱体体积是（  ）cm3

第3、4小组判断：

1.周长是12.56cm，高是3cm的圆柱，这个体积是150.72cm3（  ）

2.一个圆锥的体积是3m3，与它等底等高的圆柱体积是9dm3

第5、6小组选择题：

1.一根长2米的圆木，截成两段后，表面积增加了24平方厘米，圆木原来的体积是（  ）立方厘米？

A.48              B.240            C. 2400

2.一个圆柱底面積是9.42平方米，高是3米，与它等底等高的圆柱的体积是        （  ）

A.28.26m3      B.9.42m3        C.84.78m3

第7、8小组应用题：

1.有两个底面积相等的圆柱体，其中一个高为4.5dm，体积为81dm3，另一个高为3dm，求它的体积。

2.将一个高是6dm的圆柱沿底面半径切开，拼成一个近似的长方体，表面积增加了24dm3，这个圆柱的体积是多少立方分米？

这样巧用变式练习，既让学生灵活运用学过的知识，又发展了他们的创新精神，锻炼学生合作交流的能力。原来掌握还不够好的学生，通过这样训练，也清楚明白了。教师只是引路人，起到指导作用。学生会觉得同学出题，和同学之间讨论，和老师讨论，很亲切，难题也就迎刃而解了。

五、变式练习要遵循学生的认知规律

小学生对数学基础知识的认识过程一般遵循：机械掌握（只抓住知识的外部特征和联系）——理解掌握（认识概念的本质属性和内在联系）——灵活应用（沟通知识内在联系，从不同角度分析解决问题的过程）。思维特点是从具体形象思维到抽象逻辑思维为主要形式的逐步过渡。他们的智力发展是在心理和思维发展过程中掌握知识和技能，逐步改组，更新原有的认知结构而形成的。在数学教学中，围绕新课知识设计合理而巧妙的变式练习，鼓励和激发学生独立思考，积极探索，点燃其智慧的火花，使新知识更加牢固，又启迪了学生的思维，从而培养学生学习数学的兴趣。