以主题任务驱动数学融合学习
2019-09-10刘佳严育洪
刘佳 严育洪
摘要:在数学教学中,可以寻找学习情境之间的联系以及学习方式之间的联系,把一个单元的知识甚至不同单元的知识围绕一个主题融合成新的学习单元。西方有一句浪漫的谚语:“你在的时候你是全世界;你不在的时候,全世界是你”。借用在数学教学中,可以扩展为“数学你在的时候,你是全世界;数学你不在的时候,全世界是你”。其意为在数学课内,数学应该与“全世界”紧密相连;在数学课外,我们不仅要从“全世界”中看到数学,还应该通过数学指向其他学科知识的融合。
关键词:主题任务驱动;小学教学;融合学习;学习活动
查理·芒格说:“他的智慧,来源于他的‘思想格栅’。在这里面,每一块竖的木板,就可以看作是一个知识领域,而每一条横木板,就是知识领域之间的联系,它串联起了两个不同的领域。”
同样,在教学中,我们也可以寻找这样的“思想格栅”,把同一领域的各个知识甚至不同领域的各种知识横向融合起来,创造新的学习主题,创造新的学习任务,创造新的学习单元,创造新的学习教材。
华东师范大学崔允廓教授倡导大单元备课以提升教学设计的站位:“一个单元就是一个完整的学习故事,就是一种课程,或者说微课程。譬如语文教材中的一个单元主题下的四篇课文,如果不是一个完整的学习方案,没有学习任务的驱动,就只是内容单位,不是我讲的单元概念。”
在数学教学中,我们可以不再局限于寻找学习知识之间的联系,还可以寻找学习情境之间的联系以及学习方式之间的联系,把一个单元的知识甚至不同单元的知识围绕一个主题,融合成新的学习单元。
(一)“对比式”融合学习
一些容易混淆的概念在单个教学的时候,因为对象比较“专一”,学生思维不会发生混乱,此时教学的即时效果往往很好。但很多时候,这只是一种表面现象,因为等到把另外一个似是而非的数学概念放在一起的时候,学生的思维有时候就会产生困惑。对此,比较着学、融合着学是解决这一问题的有效策略,这样可以在第一时间内暴露学生的问题,在且行且思中逐步明晰概念。
例如,“面积”常常与“周长”纠缠不清,而教材在教学“面积”的时候并不没有结合“周长”进行辨析。对此,我们采取了带着“周长”教“面积”的融合策略,组建了综合性学习新单元。
课首,教师把一个长方形变成了平行四边形,让学生发现图形的周长相等,但面积却越来越小,从而改变了学生开始所持有的“周长相等的图形面积也相等”的错误想法,有效地使学生注意到了“面积”与“周长”所表示的不同意义。
在练习环节,教师又进一步引导学生思考(如图1),在解答原有题目之后,让学生继续观察其中的第一个图形和第三个图形,让学生发现“面积相等但周长不相等”,与课首发现的“周长相等但面积不相等”相比较后形成完整的认识,再次感受到周长与面积意义的不同。
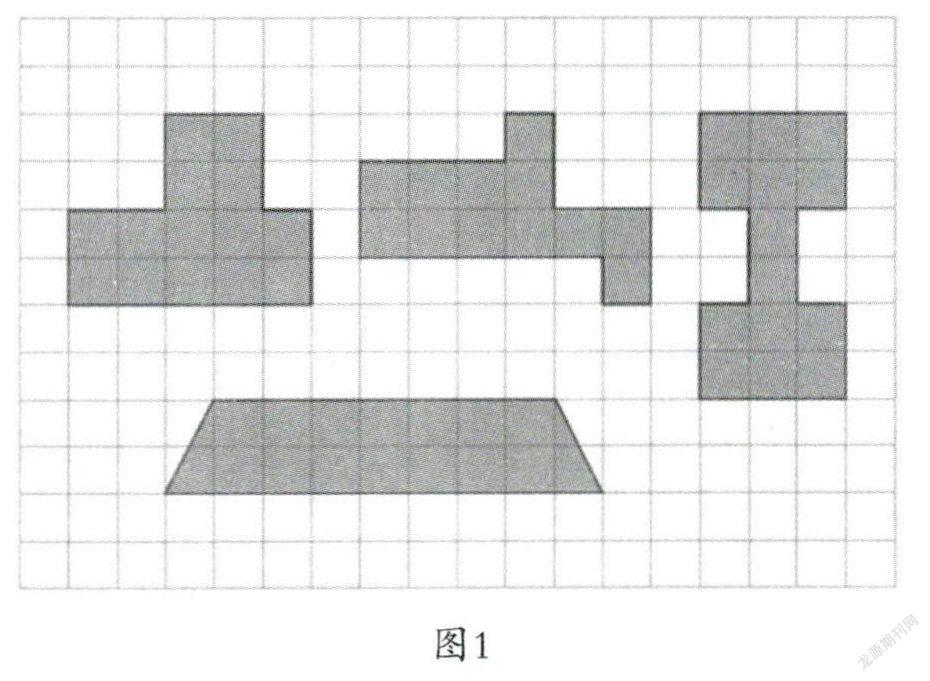
随后,教师又设计了“画一条线,把长方形分成两个图形,要求新得到的两个图形周长相等”的探究任务。从最初画对角线到过中心点画直线,直至在对角之间画曲线(如图2),学生的思维慢慢从关注面积而分成两个相同的图形中跳出来,最终能够直接抓住周长的意义来寻找更多的答案。

继而,教师又设计了“两根绳子分别长22m和24m,分别围成边长是整米数的长方形,哪根绳子围出的长方形面积大”的探究任务。这样,促成了“面积”与“周长”的融合教学,教师还趁热打铁,链接到五年级的“用一一列举的策略解决问题”一课(如图3),提前整合到一个学习大单元之中,这样的教学更具针对性和时效性。

认知心理学研究表明,碎片化学习内容的可辨识度比较低,既不利于学生的记忆,也不利于学生的理解。而“比较着学”这种融合学习,可以很好地将学习内容进行结构化设计,显著提高内容的可辨识度,有利于学生在感知、理解、辨识的基础上进行数学模型和数学模式的建构。
例如,有一位学生就對“时间、速度、路程”数量之间的关系设计了富有创造性的造型(如图4),让大家形象化地看到了它们之间的关联。
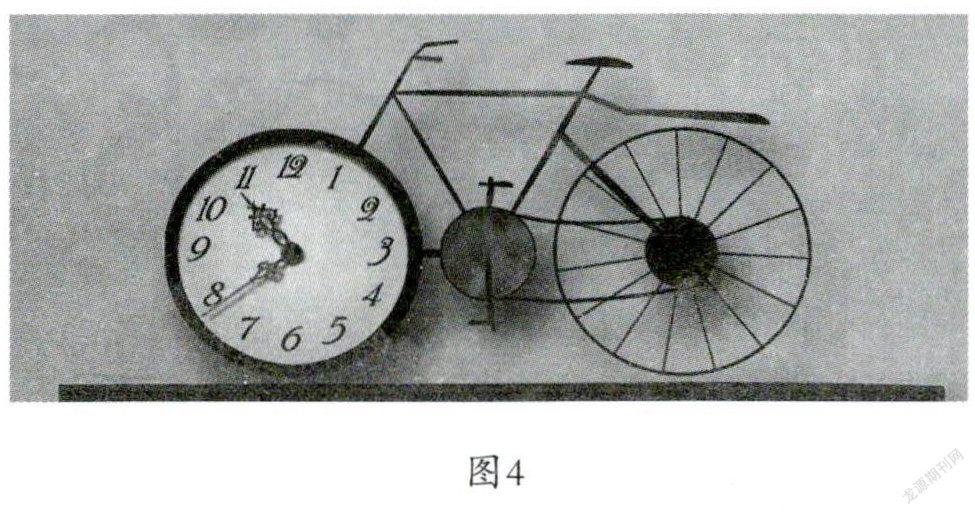
(二)“创研式”融合学习
在任务驱动学习中,我们可以设计知识的研发任务,引导学生从概念出发,根据知识之间的关系不断创造出新的知识,或者把分散于不同单元的知识融合在一起进行整体化理解与记忆。
例如,除法的知识、分数的知识、比的知识,虽然身处不同年级、不同单元之中,但教p币只需在每个单元教学的第一节课沟通了它们之间的关系,后续知识的学习中就可以让学生成为“创客”,由“商不变规律”研发出“分数的基本性质”和“比的基本性质”(如图5),这样的课就成了“创课”,学生完全有能力去设计和当“小老师”。
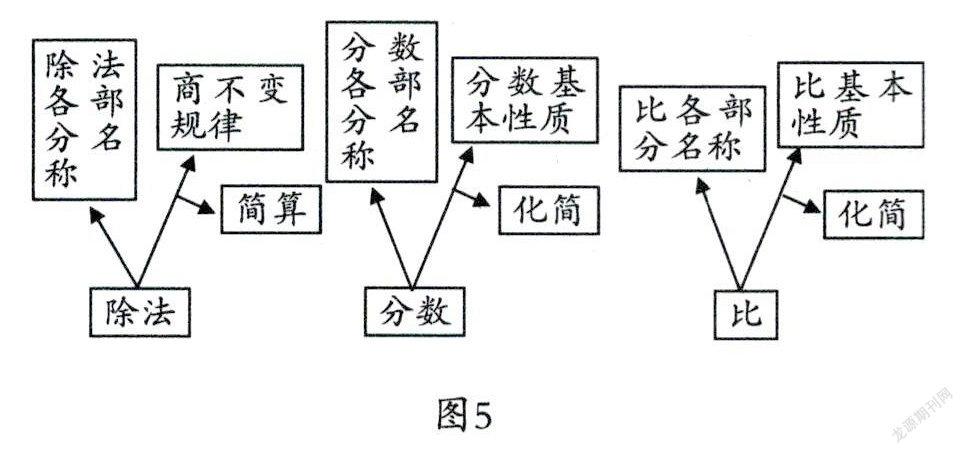
更重要的是,在知识的研发中,学生会自觉发现问题,最终明白“为何商不变规律称之为规律”,是因为它是上位知识,由它推导出了“分数的基本性质”和“比的基本性质”。当学生有了这样更深刻的理解,就会呈现这样的知识谱系图(如图6)。
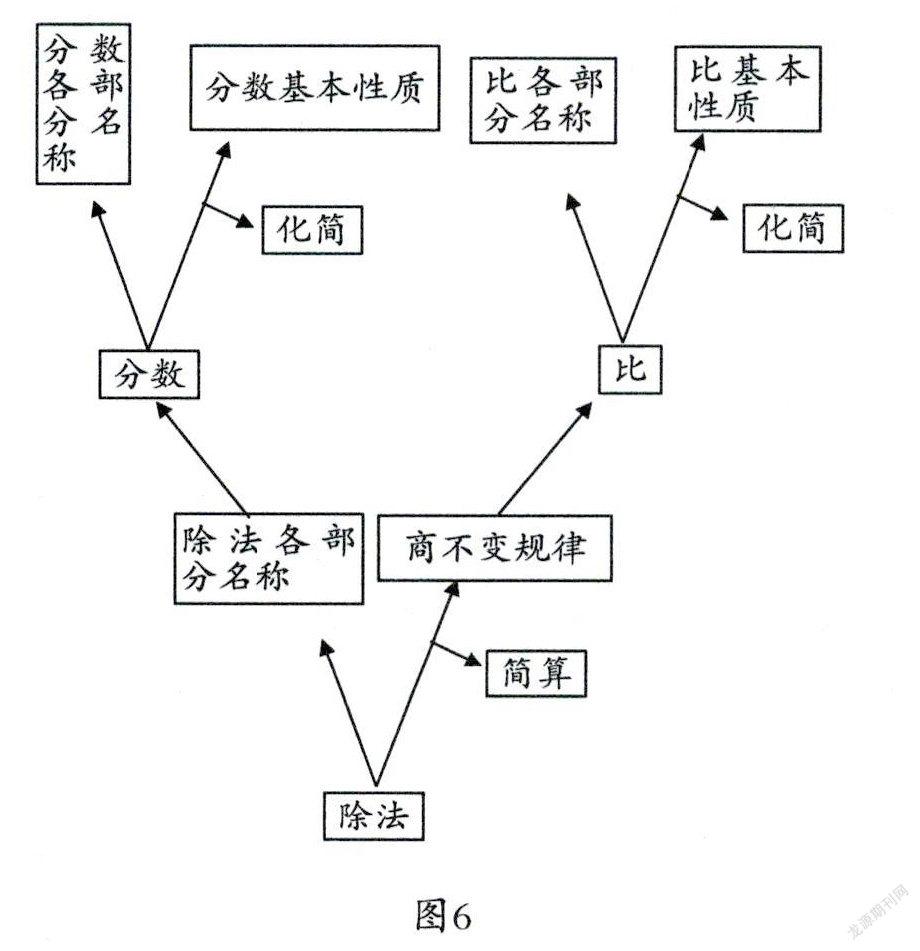
当然,我们也可以“后发制人”,通过知识回顾,引导学生寻找知识的血缘关系,重新组建成知识融合的学习大单元。此时,学生具备了知识的全景意识,看到的就不再是一棵棵“知识树”,而是一片“知识林”。
(三)“挖井式”融合学习
弗赖登塔尔认为,数学化分横向数学化和纵向数学化。在任务驱动学习中,我们可以将横向数学化和纵向数学化融合起来,设计结合现实生活的挑战性任务不断深挖知识,实现学生对数学的深度学习。其中,一旦学生的深挖触及到其它单元中的知识,此时的学习将开启新单元,展现新气象。
例如,学生在学习了“长方体和正方体的体积计算”之后,我们通过不断变换情境和条件,层层设阻,使得学生的探究层层深入。
第一步:设计“如何计算不规则的橡皮泥的体积”的延伸性任务。学生想到了捏压成长方体或正方体“等积变形”的转化方法。
第二步:把橡皮泥换成石头。学生在捏压方法行不通的情形下,想到了排水法,把石头浸入量杯后看所上升的水的体积。
第三步:把量杯换成长方体容器。学生同样可以使用排水法,但需要事先测量长方体中原有水的长、宽、高以及浸入石头后的水的高,通过计算得到石头的体积。
第四步:把工具改成长方体容器和量杯。这时有学生想到了在长方体容器中装满水,浸入石头,用量杯测量溢出的水的体积。
第五步:只给学生一个圆柱体容器。此时,所需的知识自然链接到了与“圆柱的体积计算”相关的下一册教材的新单元教学内容,留给了学生新的学习期待。
第六步:既没有量杯也没有别的容器,或石头无法放进容器,只有一块规则的长方体石头。这时,可引导学生通过称重的方法间接求出不规则石头的体积,其原理不仅“跨界”到了正比例的知识,还“跨界”到了中学所学的物理知识,后一种“不求甚解”可以让学生带着疑问走人中学物理的学习。
高斯说:“我们需要的是想法,不是符号。”数学不只是计算、测量和公式的应用,它更是一个充满变化和新发现、新发明的领域。随着上述挑战性任务“战线”的拉长和加深,学生思维的“触角”也不断延长和深入,伸向四面八方,寻求和融合更多的本学科知识甚至是外学科知识,获得更多的新发现和新发明。如此情境下的练习功能就有了衍生性,它不再是单纯的练习,还产生了新的学习,这是挑战性任务生发出来的强劲的学习驱动力。
(四)“穿越式”融合学习
在教学中,如果我们在设计任务情境时,能够沿用学生感兴趣的已有知识特别是不同领域知识的情境,就可能会勾起学生对“往事的美好回忆”。此时的学习可能会有一种穿越感,也可能会有一种亲切感和新奇感。这样,传统的知识单元之间可能就不再界线分明,知识也可能得以融合。

例如,当学生学完四年级的“可能性”(如圖7)这一课之后,到了五年级,我们就借用这个情境进一步设计游戏任务:在每个球上写上一个数,让学生任意摸出两个球,如果两个球上数的和是奇数,就可赢得一份奖品。以此替代五年级“和的奇偶性”的例题(女口图8)。可以说,学生更喜欢从玩中学,能赢得奖品也增强了学生学习的趣味性。

为了能让游戏具有戏剧性,也为了能激发学生主动探究的积极性,我们一开始写的都是偶数,学生在“总是赢不了”的情境中自觉思考“为什么”。学生在最终的发现问题中获得了“偶数+偶数=偶数”的结论。接着,我们让学生自己修改游戏规则,有的学生提出都放人写着奇数的球,在其他学生的反对中他们得到了“奇数+奇数=偶数”的结论。经过讨论,大家一致认为必须同时放入写着奇数的球和写着偶数的球,这样摸出的两个球上数的和才有可能是奇数。在活动中,学生除了能发现“奇数+偶数=奇数”的结论,还能发现“摸出的两个球上数的和是偶数比和是奇数的可能性大”这一拓展性知识。
上述情境把教材中单纯的摸球变成了摸奖,游戏的刺激度得到了升级,学生的积极性也得到了升级,知识从四年级穿越到了五年级,也从统计与概率领域穿越到了数与代数领域,情境的延续带给了学生“知识血肉相连”的学习一体感。
西方有一句浪漫的谚语:“你在的时候,你是全世界;你不在的时候,全世界是你。”如果我们浪漫地把“你”看成“数学”,那么前半句“数学你在的时候,你是全世界”,其意就是在数学课内,数学应该与“全世界”紧密相连,后半句“数学你不在的时候,全世界是你”,其意就是在数学课外,我们要从“全世界”中看到数学。而数学课外除了指向现实生活的融合,还应该指向其他学科知识的融合。
(一)“补充式”融合学习
数学教师无法弄明白和讲清楚的其他学科知识,在补充教学时,可以邀请其他学科的教师来帮忙。
例如,在讲解美术构图中的“黄金比的应用”时,就不妨让美术教师来讲,这样会更专业。如果时间允许,还可以专门配合上一节美术课。除此之外,“数学环节+美术环节”的融合还可以拓展成同一主题引领下的“数学课+美术课”的融合。
(二)“引发式”融合学习
用其他学科的知识或方式方法作为数学教学的导引,可以创设一种引人注目和引人人胜的任务效果,由此来驱动学生进行数学学习。
例如,在“轴对称图形”一课中,我们应该思考“如何让美术教师走入数学课堂成为必要”。对此,我们可以让美术教师闪亮登场,展示一技之长。在美术教师惊艳的教学活动中,在美术教师当场剪出美轮美奂的剪纸作品之时,学生也想学剪纸的满腔热情就被激发了。美术教师可以顺势告诉学生:“想学好剪纸艺术,先要学好轴对称图形的数学知识”。此时,“轴对称图形”知识的学习就成了学生完成剪纸任务的一种技术,课堂模式变成了“美术剪纸活动+数学轴对称图形知识+美术剪纸活动”的“夹心式”结构。这节融合了美术课的数学课,尽管数学依然是主体,美术只是引子,但仍有许多学生认为这节课的课题是“学剪纸”。当然,通过这节课,学生还不能完成较复杂的剪纸任务,教师顺势可以在课后组建剪纸兴趣小组,让有兴趣的学生继续深造。
(三)“情境式”融合学习
教师可以创设一种具有综合性、感染性和挑战性的生活情境,让学生置身实际情境中去产生数学学习的需要。
例如,上述“轴对称图形”一课中,除了让美术教师当场展示剪纸才艺来吸引学生的眼球,然后引入數学学习之外,我们还可以创设“过年”的情境。由于在布置环境时用到了美丽的剪纸,再由剪纸引到数学“轴对称图形”的学习,课堂模样进一步变成了“过年+美术剪纸活动+数学轴对称图形知识+美术剪纸活动+过年”的“圆通式”结构。在这样充满喜气的任务情境的渲染下,也有学生可能会认为这节课的课题是“过年”。
可以说,在这样的情境融合和知识融合的课堂中,学生的学习必定是充满喜悦之情的。如果这节课放在元旦前或春节前教学,情境效果会更好,而学生完成的剪纸作品还可以用来布置教室或家里的新年环境。
总之,知识的深度融合发展是一项系统性工程。在任务驱动的融合学习中,所设计的长线任务和长效任务,如同“放长线钓大鱼”,要能够钓到“大鱼”,一是需要“水面”宽广,也就是我们要开展有利于学习的大单元设计,二是需要引进“活水”,也就是我们要融合不同领域的知识设`计学习活动。
