点亮思维 熔铸化归思想

葛家兵

摘   要：《义务教育数学课程标准（2011年版）》中提出化归思想不仅是一种重要的解题思想，还是一种最基本的思维策略，更是一种高效的数学思维方式。构建学生化归思想体系的最好载体就是小学数学中的“火车问题”。从三个火车模型出发，深入浅出，以论述解题过程为“药引”，于具体题例中培养学生的化归思想。

关键词：小学数学;化归思想;火车问题;思维培养

中图分类号：G623.5    文献标识码：A    文章编号：1009-010X（2019）34-0031-03

火车为人类现代最重要的交通工具之一。小学数学教学中的火车问题，实质上就是以火车过桥的经典问题为基础衍生出来的火车与行人、火车与火车等等之间的问题。破解这类题型的关键就是数学化归思想的运用，教师要培养学生善于分析题中的各种信息，最终想办法将火车问题转换成我们所熟悉的基本行程问题——相遇或追及问题。

一、小试牛刀，在车与桥的经典中选树培树化归思想的“示范点”

以前学过行程问题，行程问题的基本公式及其重要变形为：“速度×时间=路程”，那么“路程÷速度=时间”“路程÷时间=速度”。这次不让人跑了，让火车跑。我们知道火车跑起来就是一长串一起动，在火车跑的过程中，我们要清楚这个简单的规律：火车头跑了多远，火车尾也就跟着跑了多远。因此，测量火车跑过的距离时，要注意一定得从火车开始时候火车头的位置量到火车停止的时候火车头的位置，或者从火车启动时火车尾的位置量到火车停止时火车尾的位置，开火车的时候有时会遇到桥或者山洞，这样一来就为火车问题增添了难度。比如下面这道题目：

例1：一列和谐号火车长420米，它以每秒钟48米的速度打算通过一座大桥，桥长540米，需要花多长时间呢？

【解析】求时间，就得用公式：“时间=路程÷速度”。根据题干，速度好办，就是每秒钟48米，可路程是多远呢？我们不妨画出线段图来仔细看看这个过程（见图1）：火车开始通过这座桥是在A处，它过完这座桥是在B处，从A处的火车头量到B处的火车头位置就是火车实际走过的路程。而这个路程通过线段图可以轻松看出来是桥的长度加上一个火车的长度，也就是420+540等于960米，火车跑过的路程和时间都知道了，那么套用公式便可以求出时间：用路程960米除以速度48米/秒，答案是20秒。

【点评】这就是最基本的火车过桥模型。解决这类问题，我们要去寻找路程、时间和速度这三个量，往往题干中会透露给我们速度和时间，关键一步就是寻找路程，对于路程的求解，我们是化抽象为直观，通过线段图描述和确定火车开始过桥（过隧道）和结束过桥（过隧道）的样子，接着找路程的时候，一定要从开始时火车头的位置量到结束时火车头的位置，我们可以简记成：头到头，尾到尾。最后，题目中的三个量，我们知道了两个量，套用公式即可求出未知量。

二、守正出新，在车与人的邂逅中调优调准化归思想的“聚焦点”

例2：花花沿着铁道边跑步，她的速度是每秒5米，一辆火车从她对面开过来，如果这个火车长1288米，速度是每秒51米，火车从花花身边通过，要花多长时间？

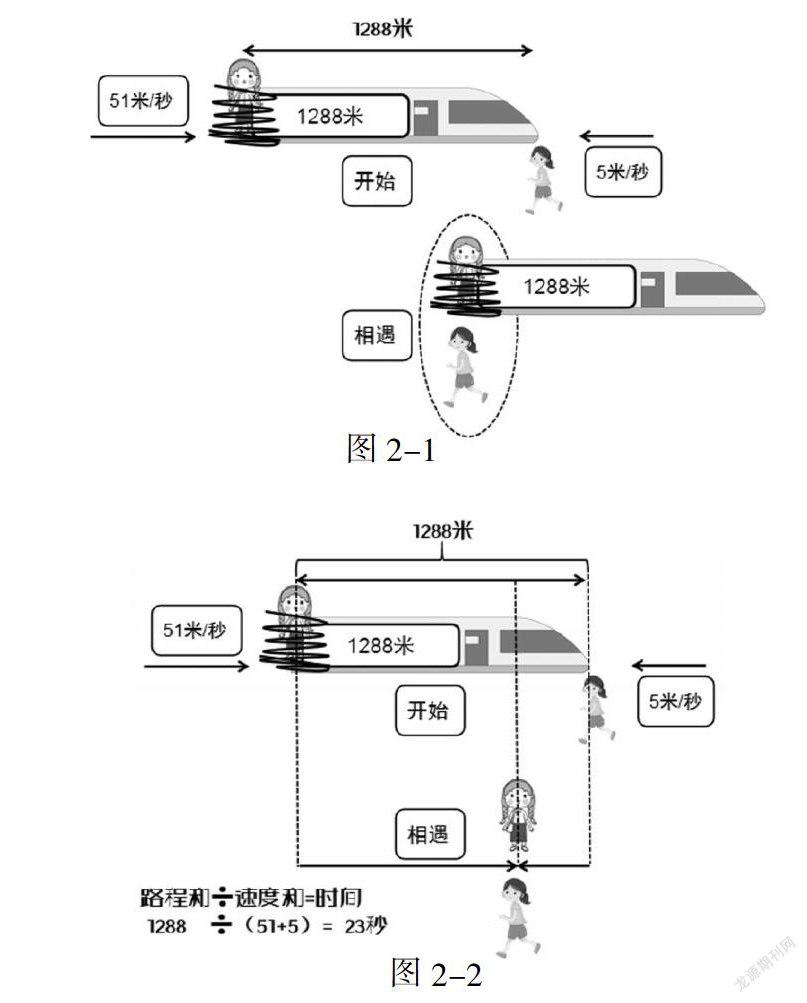
【解析】此题并不是例1中典型的火车过桥模型，而是火车与行人问题，遇到这种问题我们该怎么办呢？通过例1的学习，我们学会了怎么量火车前进的距离，一定得从头到头或者从尾到尾，既然在同一列火车上，头部和尾部运动的距离是一样的，那么我们不妨可以做出这种假想：如果在运动的火车尾上绑一个小人妞妞，火车前进的距离跟妞妞前进的距离就会是一样的，人与车绑在一起，所以前进的速度也是一样的。因此，妞妞的运动和火车的运动就是完全一样，能够意识到这个规律，我们就可以用这个小人妞妞来代表火车，用这种全新的“绑人法”就可以轻松解决火车和行人的问题了（图2-1）。

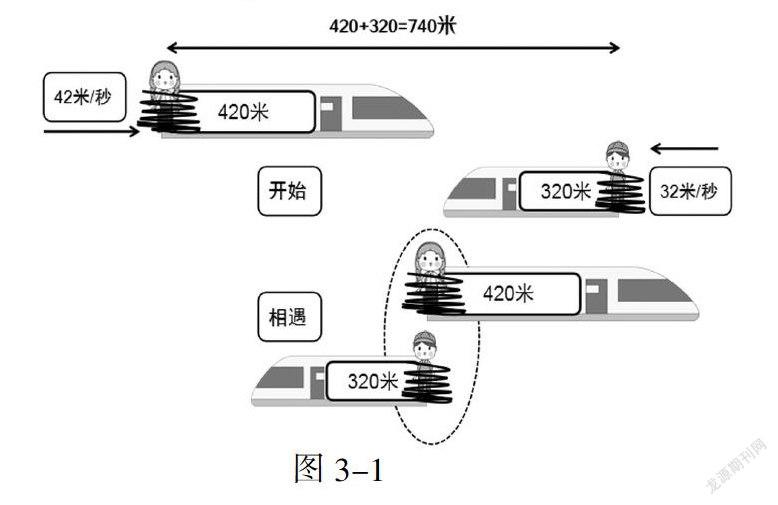
用绑人法，假设把小人妞妞绑到火车尾上。火车开始通过花花的时候是如图2-1中上图所示，妞妞和花花相距一个火车的长度也就是1288米，火车全都通过花花之后是如图2-1中下图所示，妞妞和花花就在一起了。把火车去掉，这道题目就演变成了妞妞和花花俩人的一个相遇问题，时间就等于路程和除以俩人的速度和，根据线段图可知路程和是1288米，速度和就是5+51，也就是56米/秒，两者相除就是23秒。这就是火车通过花花的时间（图2-2）。

【点拨】在这个问题里，我们使用了一种全新独家方法——“绑人法”，把火车看成一个人，就把火车与行人的问题转化成两个人的相遇问题，这样就容易做了。如果火车不是迎面开过来，而是从花花身后开过来，还是一样，先把妞妞绑在火车尾上，然后用线段图画出这个过程，去掉火车，进一步转换成一个基本的花花和妞妞两人的追及问题。不管是方向相同，还是方向不同，都可以同样用绑人法，把火车替换成车尾上的小人，接着就可以转换成普通的相遇问题或者追及问题来解决了。

三、穿越荆棘，在车与车的迷宫中延伸拓展化归思想的“精髓点”

除了把上个例题中人绑在火车尾上的“绑人法”，其实也可以把人绑在火车头上。那做题时究竟应该把人綁在哪里呢？有一个简单的判断秘诀：看看最后哪两个地方在一起，就把人绑在最后在一起的这个地方。比方说，两者最后的状态是当火车头在一起了，那么就假想出一个小人将其绑在火车头部，如果两者最后的状态是当火车尾在一起了，就把小人绑在火车尾上，这样一来，当我们去掉绑有小人的火车之后，便能转换成最基本的相遇或者追及问题。鉴于这种思路和方法，除了火车和行人问题，还可以直接将这个行人也换成一辆火车，即火车和火车的行程问题。此时，我们可以分别在这两辆火车上运用绑人法，将火车与火车问题转换成行人和行人的相遇或者追及问题。

例3：和谐号和胜利号两辆火车对着开，和谐号火车长420米，每秒钟跑42米，胜利号火车长320米，每秒钟跑32米，它俩相互错车的时间有多长呢？

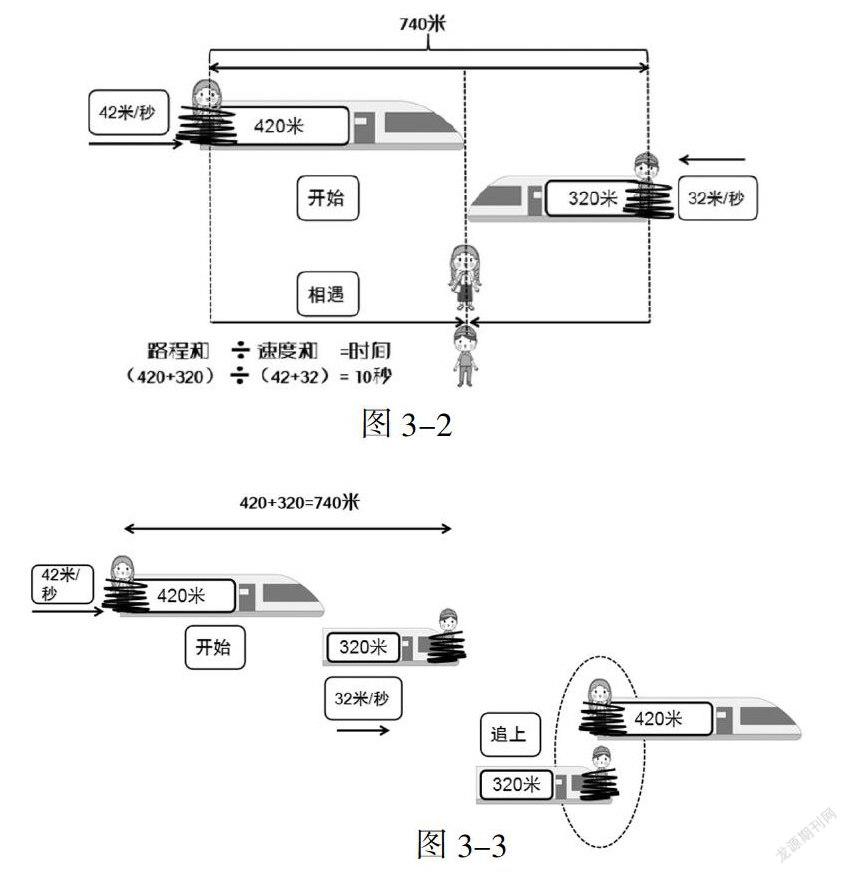
【解析】所谓错车，就是从两辆火车的头部开始相遇，一直到两辆火车尾部彻底分开的过程。根据题意，最后这两辆火车的车尾在一起，由绑人秘诀可知，应该把两个小人分别绑在这两辆火车的尾上。回到开始的时候，这两个小人还是在车尾上，它俩相距如图3-1上图所示的距离，也就是和谐号火车的车长加上胜利号火车的车长共740米。去掉火车后，我们再来看一看，如图3-2，就转换成了俩小人的相遇问题。时间等于路程和除以速度和。也就是740÷（42+32），答案是10秒。

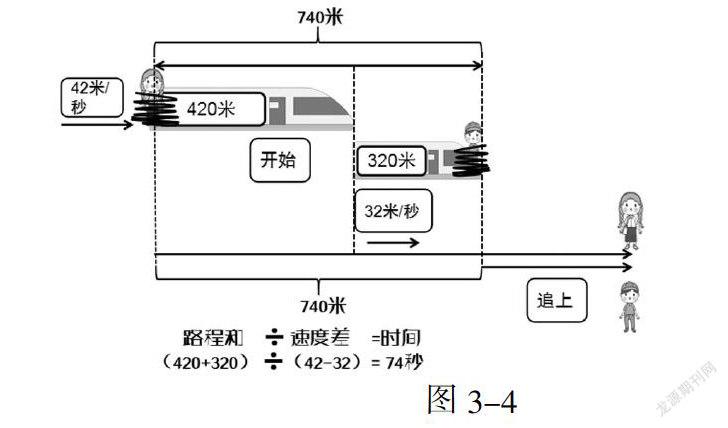
如果不是对着开而改成同向开呢？根据图3-3来分析，和谐号火车刚追上胜利号火车的时候，和谐号火车的头部和胜利号火车的尾部相遇在一起;当和谐号火车完全超过胜利号火车的时候（结束时），和谐号火车的尾部和胜利号火车的头部相遇在一起，因此两个小人就应该分别绑在结束时和谐号火车的尾部和胜利号火车的头部。回到最开始的时候，这俩小人就相距的距离就是这俩车的车长和740米。

去掉两辆火车后，这就变成了最基本的两人的追击问题。根据时间等于路程差除以速度差来求相遇时间，也就是740÷（42-32），答案是74秒（图3-4）。

【点评】火车与火车的行程问题还是用绑人法解决问题，这里用到了两次绑人法，即把两个小人分别绑在两列火车结束时在一起的位置上，再看看开始时他俩离多远，最后去掉火车，变成俩人的相遇或者追及问题就能轻松解决。