注塑成型喷射现象的实验及数值研究

2019-09-10花少震孟凡净

西安交通大学学报 2019年9期

花少震,孟凡净

(河南工学院机械工程学院,453003,河南新乡)

和简单充填模式相比,熔体喷射是一种复杂的流动模式,容易导致制品出现熔接线、喷射纹、气穴等缺陷,从而严重影响制品的力学和光学性能。1951年,Spencer等首次发现了喷射这种无规律的复杂充填模式[1]。注塑成型过程发生在闭合的型腔内,熔体充填速度快、时间短,给对喷射现象的研究带来了一定的挑战。对喷射现象的关注始于20世纪70年代,White等通过可视化手段研究了熔体的充填模式,并且认为塑料熔体的流动不稳定性并不是喷射现象发生的根源[2]。Oda等在对充填模式的可视化研究中发现喷射能发生在等温和非等温的模具型腔内,并且提出熔体模口胀大尺寸小于型腔厚度时即会触发喷射[3]。杜彬等采用可视化手段分析了模具结构、加工工艺和熔体流动之间的关系,提出了一些改善喷射现象的措施[4]。此外,严志云等和欧相麟等也总结了一些解决喷射现象的经验措施[5-6]。近年来,Krug等和Sardarian等分别采用短射实验手段研究了粉末注射成型中的喷射现象[7-8]。工程中主要通过模具设计和制品加工经验来抑制或消除喷射现象,但是由于对熔体喷射机理的认知不足,不同制品之间的模具结构往往需要反复试模以探索最优的加工工艺,甚至需要修改模具结构,这种试错法需要耗费额外的成本,所以探索触发喷射的内在机理是十分有必要的。对于触发喷射的内在机理,许多学者也进行了研究:孙翔等认为冷却作用导致了熔体射入型腔后的表皮硬化,进而导致了喷射的发生[9];Özdemir等认为触发熔体喷射的因素是熔体从浇口射出时具有紊流流动特征[10];Balkovsky等认为高分子流体的紊流特征是由其极强的弹性效应导致的[11];Groisman等发现,当高分子流体的弹性足够强时,即使其雷诺数非常低,也能表现出类似牛顿流体雷诺数约为5 000时的紊流运动[12];Zhang等通过数值模拟发现熔体的弹性会对喷射后的形态演化产生影响[13]。目前,对于紊流触发喷射的理论尚未得到验证。此外,一般认为塑料流动是一种层流,此时熔体流动过程中的惯性力可以忽略,但花少震、张世勋等通过数值模拟手段量化了惯性力和黏性力,发现惯性力大于黏性力是触发喷射的关键因素[14-15]。

本文采用短射实验和数值模拟这2种方法研究喷射现象,探索触发简单充填和喷射流这2种充填模式的关键性因素,从而为工程中模具设计和塑料制品加工提供有效的理论指导。

1 喷射现象的实验研究

本文设计的模具几何结构如图1所示,型腔为长方体(202 mm×60 mm×4 mm),浇口为矩形(6 mm×2 mm)并位于一端模壁的中央。这种模具设计不仅能够保证塑料熔体从浇口射入型腔后不会立即与模壁接触,为熔体喷射后的形态演化提供了足够的空间,而且保留了注塑成型多用来生产薄壁制品的特征。实验材料为台湾奇美公司生产的聚碳酸酯PC-110,实验前塑料在120 ℃恒温条件下干燥4个小时,注塑机型号为Demag 80/420-430。为了准确再现喷射结束后的蛇形流形态,采用短射实验研究喷射现象,保压压力为0,冷却时间20 s,注射时间为0.18 s。

图1 本文设计的模具几何结构

通过短射实验可以发现,本文所采用的奇美PC-110塑料在图1所示的型腔结构中产生了喷射行为,未发现有简单充填模式的短射制品出现,而且所有的制件均有非常明显的喷射纹或者蛇形流流动前沿,这也印证了Jain等提出的PC塑料熔体容易发生喷射现象[16]的观点。图2为在不同熔体温度和注射速率下熔体喷射后的短射实验结果,可以看出:图2a是一种稳定形态的喷射形态,图2b是一种非稳定形态的喷射形态,这2个工艺条件下的蛇形流形态在数值部分有对应的算例;喷射后的流动前沿演化复杂多变,容易带来一些制品缺陷,例如图2e和2f在近浇口区域有非常明显的喷射痕,图2c、2d和2g样品内出现了明显的裹气。调整模具温度、注塑速率、熔体温度等加工工艺后进行实验,发现模具温度对熔体在型腔内的充填模式影响不大,与Oda等观察到的实验结果[3]一致。由于喷射发生的时间短,熔体和模具的接触面积远小于简单充填模式下的接触面积,所以模具温度对喷射后的蛇形流演化影响较小。但是,注射速率和熔体温度却能对蛇形流的演化产生影响。

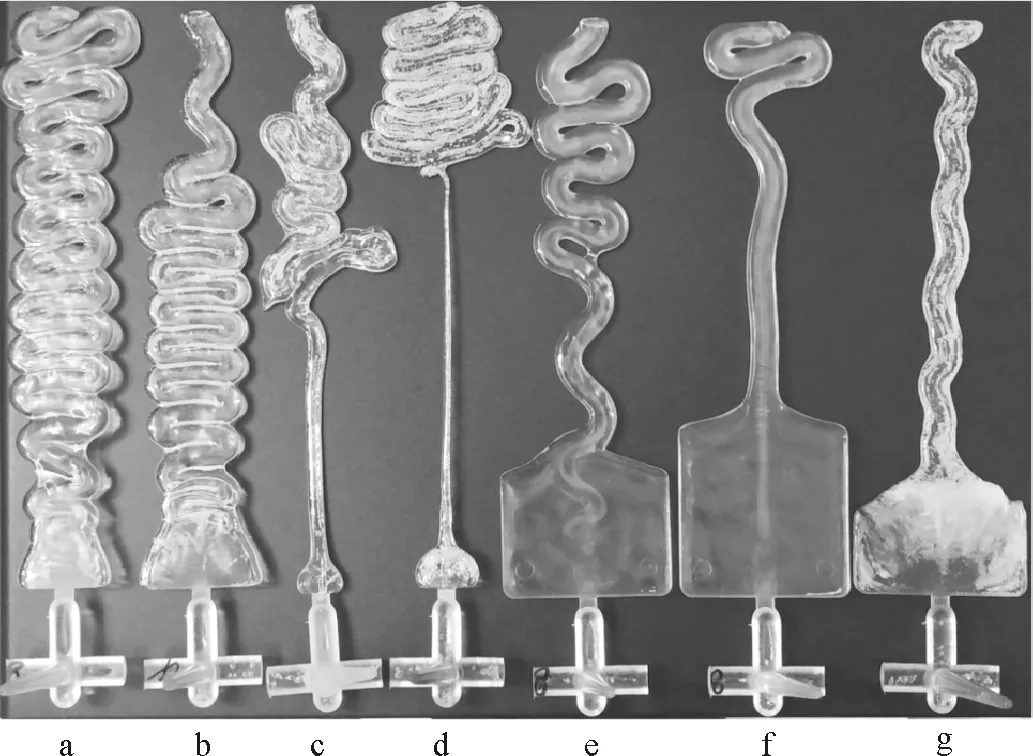
a:300 ℃,80 cm3/s; b:290 ℃,100 cm3/s; c:270 ℃,80 cm3/s; d:260 ℃,80 cm3/s; e:280 ℃,80 cm3/s; f:260 ℃,100 cm3/s; g:250 ℃,100 cm3/s图2 不同熔体温度和注射速率下熔体喷射后的短射制品

从不同熔体温度和注射速率的组合实验发现,熔体喷射具有较大的不稳定性,细小的差别如注塑机的精准控制、熔体宏观和微观性质的不均一性均可能导致蛇形流的形态发生较大改变,甚至影响了在同一个工艺参数下短射制品的蛇形流形态的可重复性。通过大量的短射实验发现,熔体喷射后蛇形流形态的可重复性较差,仅当熔体温度和注射速率为300 ℃和80 cm3/s以及260 ℃和100 cm3/s时,喷射后的流动前沿具有较高的相似度,如图3所示。当熔体温度为300 ℃时,蛇形流的形态如同压缩的弹簧,因为熔体的温度高,黏度较小,所以熔体易于流动,折叠次数远多于260 ℃下蛇形流的折叠次数。2种工艺条件下的平均折叠次数分别为19.6次和8.6次。

(a)300 ℃,80 cm3/s

(b)260 ℃,100 cm3/s图3 2种加工工艺下的短射制品

对比2种工艺参数下的蛇形流形态可发现,温度越高,蛇形流的折叠幅度越大,折叠次数也越多。从图3中蛇形流的折叠可以发现,蛇形流的第1次折叠倾向于偏向同一个方向(图中向左)。对图3中2种工艺各进行30次短射实验,结果如下:工艺条件为300 ℃和80 cm3/s时,蛇形流第1次折叠偏向右边的次数为4次,出现的概率为0.133;工艺条件为260 ℃和100 cm3/s时,仅得到22个如图3b所示的稳定蛇形流形态,蛇形流第1次折叠偏向右边的次数为2次,出现的概率为0.091。

2 喷射现象的数值模拟

短射实验虽然可以判断熔体是否发生喷射,并且可以得到熔体喷射后的最终形态,但是无法体现喷射后的流动前沿演化过程,而且难以通过短射实验来定量分析触发喷射的内在机理。但是,数值模拟能完整地再现塑料熔体在型腔内的喷射演化过程。对于喷射现象的数值模拟:Chau等认为喷射具有三维特征并且需要考虑惯性力的作用[17];Michaeli等考虑熔体惯性作用,用商业软件成功模拟了熔体喷射,结果表明当忽略惯性作用时,不会有喷射现象的发生;文献[14,19]验证了这种理论,考虑了熔体流动过程中的惯性,采用实体模型,发展了数值算法,成功模拟了注塑成型中的喷射现象。假设喷射过程中型腔排气良好,则不可压缩、非等温熔体流动的控制方程为

(1)

(2)

其中“∶”代表张量的双点积。

本文采用7参数的Cross-WLF模型表征塑料熔体黏度随温度、剪切速率、压力的变化,公式为

(3)

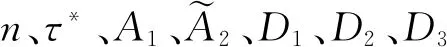
表1 PC-110塑料的物性参数

与简单充填模式下的流动前沿相比,熔体喷射后的流动前沿演化复杂。本文采用流体体积模型追踪流动前沿的位置,熔体的充满程度φ需满足

(4)

为求未知量u、p、T、φ,采用有限体积法离散所有偏微分方程。针对这些未知量的高度耦合性以及熔体黏度对温度和剪切速率的依赖性,本文采用2重迭代求解算法。第1重迭代使用PISO算法[20]求解速度和压力场;第2重迭代以速度为已知量,求解温度场,然后利用速度场和温度场更新黏度,重新求解速度、压力、温度,得到新的速度场后更新流动前沿。为了准确追踪喷射后流动前沿的演化,式(4)中的对流项的离散采用高精度的CICSAM[21]格式。对于求解过程中的边界条件,入口处速度采用固定值,温度采用熔体的加工温度,压力采用第2类边界条件;模壁处压力采用无渗透边界条件,速度采用滑移边界条件,温度采用第3类边界条件。假设型腔的排气良好,可以忽略熔体喷射过程中空气与熔体之间的相互作用,因此熔体前沿的压力等于大气压,可以假定为0。关于喷射现象数值模拟的详细算法可参见文献[19]。

2.1 稳定形态的喷射数值模拟

从图3可以看出,2种加工工艺下熔体喷射后的形态演化呈现出相对稳定的状态,因此在2种工艺下均可以得到非常相似的流动前沿形状。本节采用实体模拟技术,模拟了熔体喷射后的形态演化过程,模拟条件分别与图3中的2种工艺条件相同。本文所有模拟采用的几何模型及尺寸均同图1所示,而且模具温度均等于50 ℃。图4为2种工艺条件下,型腔中面上熔体充填形态图,对比图3和图4可以发现:在相同工艺条件下,数值模拟结果和实验结果均比较吻合;特别是在熔体温度和注射速率为300 ℃和80 cm3/s的工艺条件下,数值结果和实验结果非常吻合,熔体喷射后的流动形态均呈压缩的蛇形流。2种工艺参数下模拟的蛇形流的折叠次数分别为20次和8次,与实验呈现的平均折叠次数分别相差0.4次和0.6次。

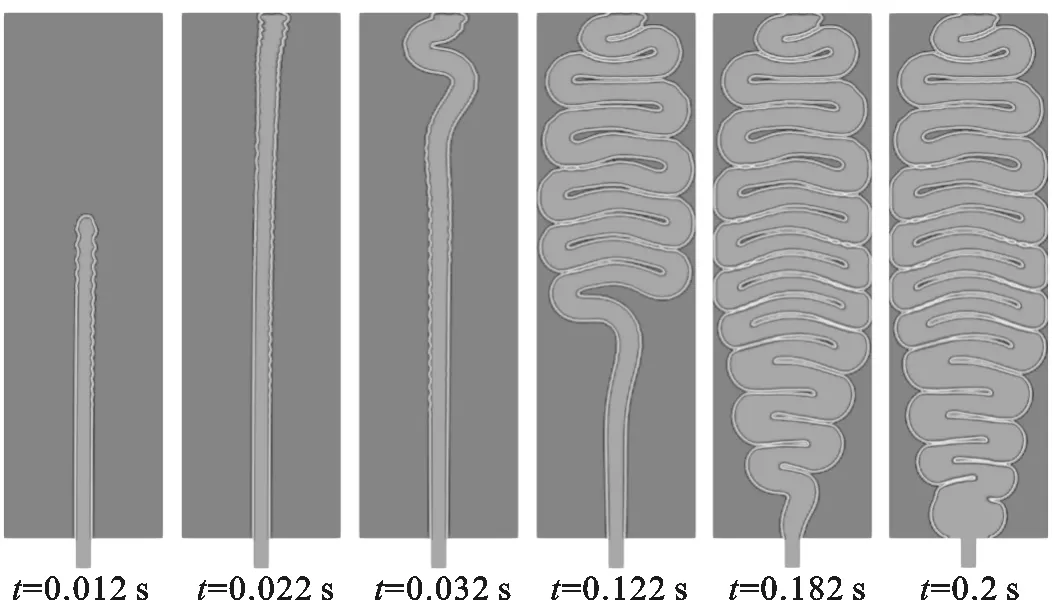
(a)300 ℃,80 cm3/s

(b)260 ℃,100 cm3/s图4 2种加工工艺下熔体喷射后的演化过程

通过观察不同时刻的充填形态图可以发现:塑料熔体从浇口射出后不与模壁接触,并且以柱状向前发展,此时熔体与模壁之间没有热交换以及摩擦作用;当柱状前端到达与浇口相对的模壁后,在模壁阻力的作用下,前端停止流动,并阻碍后续熔体流动,后续熔体在惯性以及这种阻碍作用下发生屈曲;由于薄壁制件的厚度远小于其长度和宽度,型腔厚度不满足熔体屈曲所需要的空间,所以柱状熔体的屈曲方式为柱状熔体在型腔中面上的折叠;熔体屈曲由柱状前端向浇口发展,在这个过程中,熔体和模壁的接触面积也逐渐增大;当屈曲发展到浇口后,熔体的充填模式转化为简单充填模式。综上可知,熔体从浇口射出后发生喷射一般会经历3个阶段:柱状喷射阶段、屈曲流演化阶段、简单充填模式阶段。在柱状喷射阶段,塑料熔体从浇口射出后以长直的柱状发展到与浇口相对的模壁,然后喷射转入屈曲流演化阶段,这个阶段熔体由柱状前端开始屈曲直至浇口,对于薄壁制品,柱状熔体屈曲后的形态为蛇形,当屈曲发展至浇口后,熔体充填转化为简单充填模式。

2.2 非稳定形态的喷射数值模拟

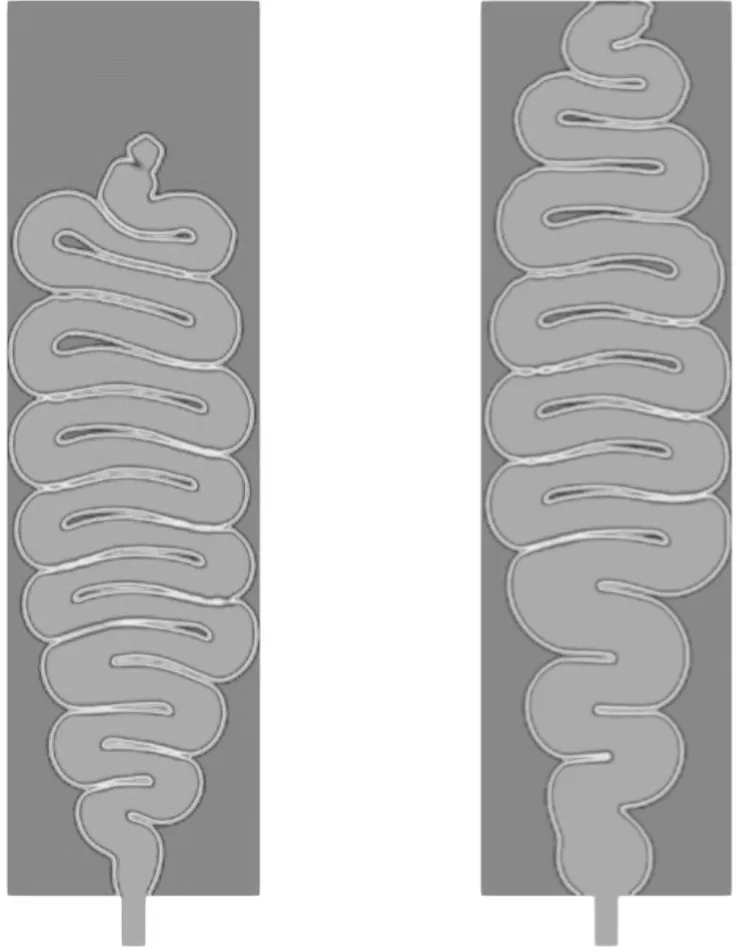
(a)低速20 cm3/s (b)高速100 cm3/s图5 300 ℃时低速和高速注射下的熔体喷射模拟形态图

本节通过调整注射速率和熔体温度模拟不同工艺下喷射后的流动形态。在低速注射中,熔体喷射受注射速率的影响较大,注射速率越大,喷射越远[14];在高速注射中,短射实验结果表明熔体喷射后均会到达与浇口相对的模壁。低速时熔体喷射距离受惯性、黏性力以及重力互相竞争的影响,而高速时则是熔体惯性占绝对主导地位。图5为300 ℃时低速(20 cm3/s)和高速(100 cm3/s)注射下的熔体喷射模拟形态图,可以发现:低速时熔体喷射后柱状前端停在型腔中某一处,喷射距离与速度有关;高速时熔体前端到达与浇口相对的模壁。对比图4a和图5b可以发现:在2种注射速率下,熔体喷射均到达模壁,且蛇形流形态相似;注射速率为100 cm3/s(较高速)时的折叠次数为17次,小于注射速率为80 cm3/s(较低速)时的20次,这是因为虽然惯性力占主导地位,但是和较高速相比,较低速为蛇形流演化提供了较多的时间;较低速时的折叠幅度大于较高速,这和低速注射时的喷射结果[14]规律相同。

图6为注射速率为100 cm3/s时熔体温度分别为270、280、290 ℃时的熔体喷射模拟形态图,可以发现,随着熔体温度的升高,蛇形流折叠次数逐渐增多。熔体温度和蛇形流折叠次数的关系如图7所示,可以发现,蛇形流折叠次数和熔体温度在熔体温度为260～300 ℃时呈线性关系。

(a)270 ℃ (b)280 ℃ (c)290 ℃图6 注射速率为100 cm3/s时不同温度下的熔体喷射模拟形态图

图7 熔体温度与蛇形流折叠次数的关系

3 机理分析

从稳定形态和非稳定形态的数值模拟中可以发现,熔体喷射后具有3个相同特征:一是熔体喷射后的流动形态发展均经历3个阶段,而且在柱状喷射阶段的流动形态相同,均为长直的柱状;二是喷射的流动形态最终发展成蛇形,但是蛇形流的形态不相同,折叠次数及幅度均有差异;三是柱状熔体屈曲发展至浇口后均转化为简单充填模式。由于柱状喷射是熔体发生喷射后的第1个阶段,所以可以认为,触发喷射现象的因素即是触发柱状喷射的因素,也是决定熔体充填模式的关键性因素。为了探索触发喷射现象的关键性因素,本节以熔体喷射后的第1个阶段即柱状喷射阶段为研究对象,分析熔体喷射后各物理量的分布规律。

3.1 剪切速率的分布规律

当熔体温度和注射速率为300 ℃、80 cm3/s时,柱状喷射中线上的熔体剪切速率在各充填时间的变化曲线如图8所示,各曲线之间的充填时间间隔Δt=1.5 ms,可以发现:流道中熔体的剪切速率较大,量级达到O(103),与简单充填模式下流道内剪切速率的量级相同,这是因为熔体受来自模壁的摩擦作用,熔体各层之间内摩擦较大,因此剪切速率较大;当熔体从浇口射出后,剪切速率骤降,在柱状前端剪切速率降至10-2s-1以下,甚至达到10-4s-1以下;当柱状喷射距离(柱状前端到浇口距离)小于141.5 mm时,剪切速率呈下降趋势;当柱状喷射距离超过141.5 mm后,剪切速率先缓慢增大后急剧降低,但是在到达模壁前数量级依然小于O(101)。

图8 中线上熔体剪切速率的变化情况

3.2 黏度的分布规律

当熔体温度和注射速率为300 ℃、80 cm3/s时,柱状喷射中线上的熔体黏度和零剪切黏度比(μ/μ0)在各充填时间的变化曲线如图9所示,各曲线之间的充填时间间隔Δt=1.5 ms,可以发现,当柱状喷射距离小于150 mm时,零剪切黏度比趋近于1,熔体黏度趋近于零剪切黏度。这是因为柱状喷射时间非常短,而且熔体从浇口射出不与模壁接触,熔体温度变化较小。又由于熔体的剪切速率小于10-1s-1,所以熔体的黏度趋近于零剪切黏度,黏度比曲线呈平台状,熔体可以近似认为是牛顿流体。

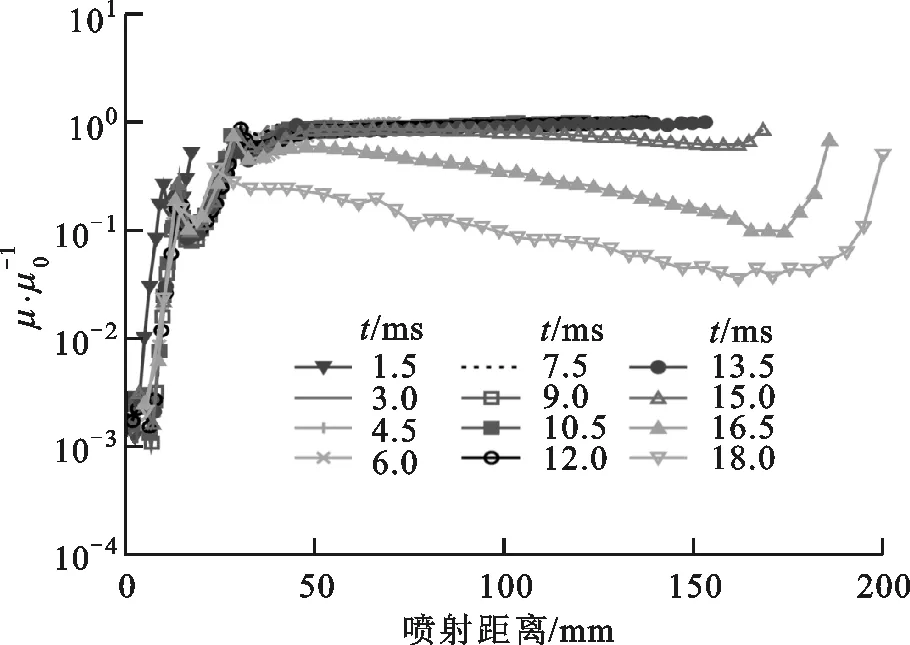
图9 中线上熔体黏度比μ/μ0的变化情况

3.3 速度和压力的分布规律

当熔体温度和注射速率为300 ℃、80 cm3/s时,柱状喷射中线上的熔体速度和压力在各充填时间的变化曲线如图10和图11所示,各曲线之间的充填时间间隔Δt=1.5 ms。从图10可以发现:速度在浇口处的最大值达到6.8 m/s,当熔体射入型腔后速度骤降至1.65 m/s,然后保持恒定,当柱状前端将要达到与浇口相对的模壁时,速度逐渐减小至0.68 m/s。从图11可以发现:压力在浇口处的最大值达到6.2 MPa,当熔体射入型腔后压力骤降至趋近于0,而且不随喷射距离的增大而有明显变化,说明熔体喷射不属于压力驱动流。

图10 中线上熔体速度的变化情况

图11 中线上熔体压力的变化情况

3.4 触发喷射现象的关键性因素分析

在简单充填模式下,熔体从浇口射入型腔后立即与模壁接触,受到来自模具钢的摩擦作用,并且与模具钢有热交换,所以此时在型腔厚度上的剪切速率、熔体速度、温度均呈抛物线型分布,熔体剪切速率在中心层最小、在上下模壁处最大,熔体速度、温度在中心层最大、在上下模壁处最小。但是,对于喷射流,由于熔体从浇口射入型腔后不与模壁接触,所以没有受到来自模具钢的摩擦作用,而且熔体只和空气进行热交换,因此与简单充填模式相比,熔体喷射后的热量损失较小。通过数值模拟结果发现,熔体温度的变化小于0.3 ℃,所以可以认为在理想情况下喷射后的熔体在厚度方向上的速度大小和温度均保持不变,分别等于注射速率和熔体温度。3.1节剪切速率的分布规律显示,剪切作用在柱状喷射前期对熔体流动的影响非常小,因此可以认为在理想情况下喷射后熔体的剪切速率为0。图12为简单充填和柱状喷射模式下型腔厚度上的剪切速率、速度、温度的分布规律对比示意图,其中各个量的曲线上最大值和最小值所在位置用虚线标出。

图12 2种充填模式下型腔厚度上的熔体剪切速率、速度、温度的分布规律示意图

一般认为,塑料熔体的流动为典型的层流运动,在简单充填模式下,熔体射入型腔即受到来自模具钢摩擦力的阻碍作用,致使模壁处的层流速度小于中心层速度,各层之间有相对位移并且产生较大的内摩擦。由于塑料熔体为高黏流体,内摩擦的阻碍作用使得熔体速度大小和方向均改变,产生较大的速度梯度u,所以此时熔体的黏性作用占主导地位并且阻碍熔体的流动。为了克服这种黏性作用,熔体充模需要较高的压力驱动,因此熔体的简单充填模式是一种压力驱动流。对于喷射现象,熔体射入型腔后不与模壁接触,没有受到模具钢的摩擦作用,熔体流动缺少外部阻力,导致各层熔体之间的内摩擦作用非常小,熔体各层之间没有相对位移,熔体保持原有的趋势继续向前运动,充模表现为柱状喷射,此时熔体的速度大小和方向均不会发生,速度梯度u近似为0。虽然此时熔体的黏度大于简单充填模式下熔体的黏度,但是熔体的黏性作用非常小,流动所受的阻力非常小,熔体喷射受惯性作用驱动。基于Ribe将流体屈曲划分为黏性驱动、重力屈曲、惯性—重力屈曲、惯性驱动4种模式[22],本文认为熔体的喷射现象属于惯性驱动模式。

基于以上分析,本文认为导致熔体喷射的关键性因素是熔体流动时各层之间缺乏内摩擦,在数值上的表现是熔体的剪切速率远小于简单充填模式下的剪切速率。熔体各层之间的内摩擦的外部驱动是来自模壁的摩擦作用或者说是来自模壁的剪切作用,所以模具设计时可以将浇口紧贴模壁边缘以增大摩擦作用,从而抑制喷射现象。